基于网络拓扑的子网络OD需求估计

孙 超 程 琳 栾 鑫 凃 强 马 捷

(东南大学交通学院, 南京 210096)

基于网络拓扑的子网络OD需求估计

孙 超 程 琳 栾 鑫 凃 强 马 捷

(东南大学交通学院, 南京 210096)

为了对局部交通路网进行设计和评价,运用拓扑结构分析方法对子网络OD需求进行估计.根据子网络拓扑结构,分别对子网络边界点和内部点的OD量进行分析,每个与外界网络相连的边界点都为子网络的交通发生吸引点,内部点OD需求量与原来网络保持一致.进而建立了基于网络拓扑的子网络OD需求估计模型,其中目标函数同时考虑了交通需求的熵最大化及弹性化,约束条件为子网络OD量约束.将原问题分为求解交通需求和道路阻抗两部分,设计了启发式迭代算法反复求解,并运用凸组合算法计算交通需求.运用Sioux Falls网络对算法和模型进行了测试,结果表明考虑弹性需求的子网络OD估计模型在可靠性和计算精度上均优于考虑固定需求的子网络OD估计模型,算法能够快速收敛到所需精度,建立的模型可以用来对实际路网进行简化.

OD矩阵估计;子网络分析;拓扑结构;弹性需求;启发式迭代算法

近年来,我国城镇一体化进程加快,新建城市用地、城市道路改造随之进行,这些新建、改建用地会对周边交通产生较大的影响[1].交通规划者通常不关注新建、改建用地对整个城市路网的影响,希望把研究范围聚集在感兴趣区域,这就需要在一个子网络水平下评估和分析交通网络特性[2-3].子网络是整体网络的一部分,它们之间拥有一些共同的空间和物理特性.例如,一个城市中心交通网是整个城市交通网络的子网络,一个城市铁路网络是整个城市交通网络的子网络.

全网络OD估计问题是在先验OD矩阵(根据历史数据调查获得)基础上,利用一些观测到的路段流量去预测OD出行矩阵.而实际路网中,很难获得子网络的先验矩阵,这是由于很难观测到过境交通穿过或到达子网络的数据.因此,子网络OD估计是在已知整个城市网络OD的条件下,根据道路的拓扑结构和道路属性来预测子网络OD出行矩阵,这一OD量不仅包含子网络内部小区的OD量,还包含子网络外部小区在子网络交通量的叠加.因而子网络OD估计的难点在于推断子网络内外交通联系.

根据研究范围将已有的子网络OD估计方法分为3类:① 基于全网络交通叠加的子网络OD估计[4-5].对于用户均衡网络,评估子网络OD最简单的方法就是先对全网络进行交通分配,然后将所有路径流量叠加.② 基于子网络外部网络简化[6-8].构建子网络外围的人工弧,运用网络转换法对子网络外围拓扑结构进行简化,计算出每条人工弧的费用函数,以形成一个简化后的新的全网络结构.③ 基于子网络道路流量约束的OD估计[9-10].仅考虑子网络本身,对全网络进行用户均衡分配,运用子网络道路上的流量作为输入变量,寻求需求熵最大化的OD矩阵.

尽管上述文献运用不同方法对子网络OD估计进行了研究,但仍然存在一些不足:① 基于全网络交通叠加和子网络外部网络简化的方法将研究重点几乎都放在子网络外围,但实际路网中研究对象为子网络,这2种方法需要花费大量时间处理外围网络,影响了工程应用效率;② 基于子网络道路流量约束的方法虽然应用简单,但该方法仅考虑路段流量约束,而未考虑原有OD固有属性,以及子网络与外部网络的联系.因此,本文从子网络拓扑结构入手,根据子网络边界点流量进出特性分析边界点OD吸引与发生总量,而子网络内部OD点的吸引与发生总量、OD点间的OD量与原网络保持一致.进而建立基于子网络拓扑的OD需求估计模型,该模型同时考虑了交通需求的熵最大化和弹性变化.然后将原问题分解为分别求解交通需求和道路阻抗,设计了启发式迭代算法反复求解交通需求和道路阻抗,其中交通需求运用凸组合算法计算.

1 子网络OD需求估计模型

1.1 子网络拓扑与OD需求分析

在建立子网络OD矩阵估计模型前,首先分析子网络拓扑结构和结点特性,从而得到子网络OD需求的一些信息.

1) 子网络边界OD点转换.子网络边界OD点可以用一个非OD点和新的OD点(辅助OD点)来代替,如图1(b)所示.其中非OD点和辅助OD点间的路段流量为原OD点的总吸引量和总发生量,该路段相当于TransCAD中的质心连杆.

2) 边界点需求分析.如果边界点与外围网络只有1条路段相连(见图1(a)中的点2,3,5,8,9,12,14,15),该点在子网络中的总发生量为外部网络进入该点的交通量(见图1(c)中点12的x1),总吸引量为该点流入外部网络的交通量;如果边界点与外围网络有2条及以上的道路相连(见图1(a)中的点1,4,13,16),假定该点在子网络中的过境交通被视为点内部交通量转移(见图1(d)),那么该点在子网络中总发生量为该点到子网络内部出弧的交通量和(见图1(e)中点13的x4+x6),同理总吸引量为所有入弧交通量和.

3) 子网络内部结点需求分析.子网络内部OD点总发生量和吸引量与原网络保持一致.本文假设内部OD点间的OD量也与原网络保持一致,这一假设与实际网络是相吻合的,例如从点6到点11,实际中很少有出行者从点6出发,先行驶到子网络外部,再进入子网络从而到点11.

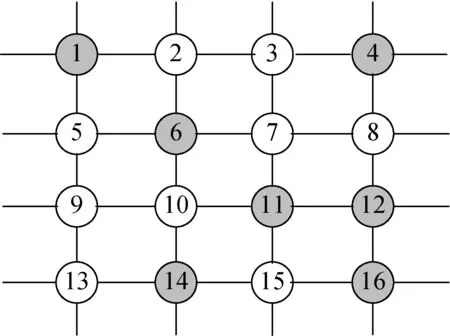
(a) 子网络拓扑

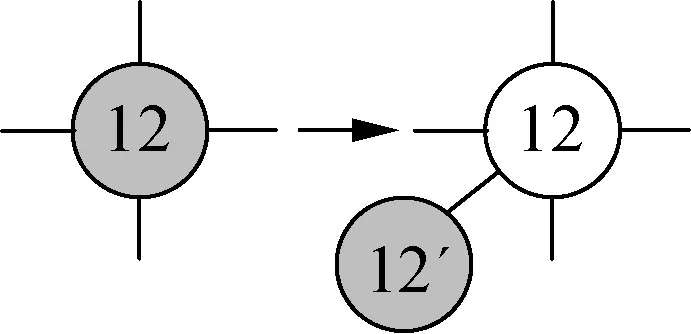
(b) 边界OD点转换(c) 只有1条路段与外界相连点分析

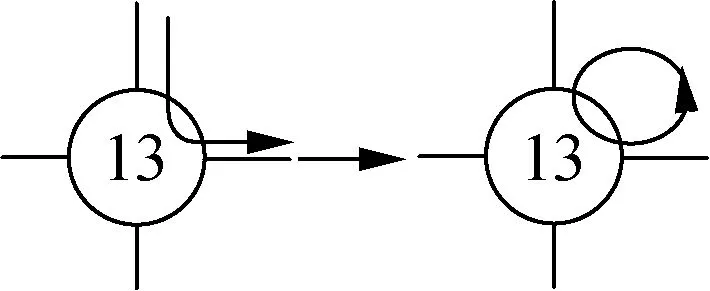
(d) 交通流量转换(e) 2条及以上路段与外界相连点分析

1.2 模型建立

考虑一个交通网络G=[N,A],其中N和A分别表示结点和路段集合.令R和S分别表示子网络起点和终点的集合,qrs为OD对r∈R,s∈S间的交通需求量.运用交通需求熵最大理论和交通弹性需求方法建立子网络OD需求估计模型,根据1.1节中对子网络边界点和内部点OD总量的分析,建立了如下基于子网络拓扑的OD需求估计模型:

(1)

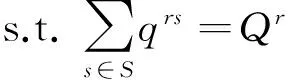
(2)

式中,Drs(·) 为起点r与终点s之间的弹性交通需求函数;trs为起点r与终点s之间的道路阻抗;Qr和Qs分别为结点r和结点s总交通发生量和总吸引量,子网络所有OD点的Qr和Qs均可通过1.1节的方法获得;C为常数,即子网络内部点间的OD量为已知常数;Ω为OD量已知的点集.目标函数(1)的左半部分为需求最大熵公式,右半部分为弹性需求与实际需求的欧氏距离最短公式.该模型得到的子网络OD值为近似的交通需求,虽然与实际值存在一些偏差,但在实际工程应用中已能够满足需求.

可行域即式(2)是非空闭凸集,且式(1)是关于需求q的正且连续函数,因此建立的模型至少存在1个解.目标函数关于交通需求的黑森矩阵为正定矩阵,因此目标函数是严格单调的,同时由于可行域是凸的,因此模型具有唯一解.

2 启发式迭代算法

弹性需求函数Drs(trs)中道路阻抗trs是交通需求qrs的函数,因而很难运用一般的下降算法(如最速下降法、牛顿算法等)来求解建立的模型.本文设计了启发式迭代算法来求解基于网络拓扑的子网络OD需求估计模型,这种算法将复杂的原问题简化为2部分:① 固定道路阻抗求解交通需求;② 根据新的交通需求求解道路阻抗,通过不断迭代最终得到最优的交通需求.本文设计了凸组合算法求解第1部分,对式(1)中的目标函数进行泰勒展开(此时道路阻抗为固定值),并用一阶泰勒展开式代替原目标函数,这样原非线性规划问题(1)和(2)可转换为下面的线性规划问题[11]:

(3)

约束条件为式(2).该问题为经典的运输问题,其中运输价格为lnqrs(n),本文使用表上作业法[12]来求解该运输问题.启发式迭代算法的具体步骤如下:

1) 初始化.对全网络进行用户均衡分配,得到子网络及与子网络相连路段的交通量;根据1.1节子网络拓扑结构分析,得到子网络OD点的总发生量Qr、总吸引量Qs和子网络内部OD点间的交通需求qrs,∀rs∈Ω.令初始迭代次数m=0,收敛误差ε,设定初始运价crs(0)=lnqrs-2(Drs(trs)-qrs)=0,进而运用表上作业法获得初始OD需求q(0);根据q(0)计算初始道路阻抗t(0).

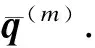
① 更新运输价格crs(n).

② 下降方向,根据运价crs(n),使用表上作业法计算OD需求q′(n).

③ 运用一维搜索方法计算步长λ(n).

④ 更新OD需求,即q(n+1)=q(n)+λ(n)(q′(n)-q(n)).

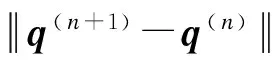
4) 对交通需求q(m+1)进行用户均衡分配,得到道路阻抗t(m+1).

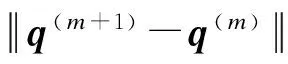
设计的启发式迭代算法在Visual Studio 2015环境下运用C#语言编程,同时在配置为Intel(R) Core(TM) i7-5600U CPU 2.60 GHz,8 GB内存的笔记本电脑上测试算法.该算法的收敛速度主要受初始化中最短路径搜索和下降方向中闭回路搜索影响.本文采用Dijkstra算法进行最短路径搜索,该算法的复杂度为o(n2);在寻找闭回路时,本文采用深度搜索算法,并在邻接矩阵上遍历所有变量,复杂度也为o(n2).该算法收敛速度满足实际工程的需求.

3 算例

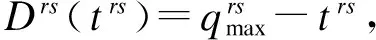
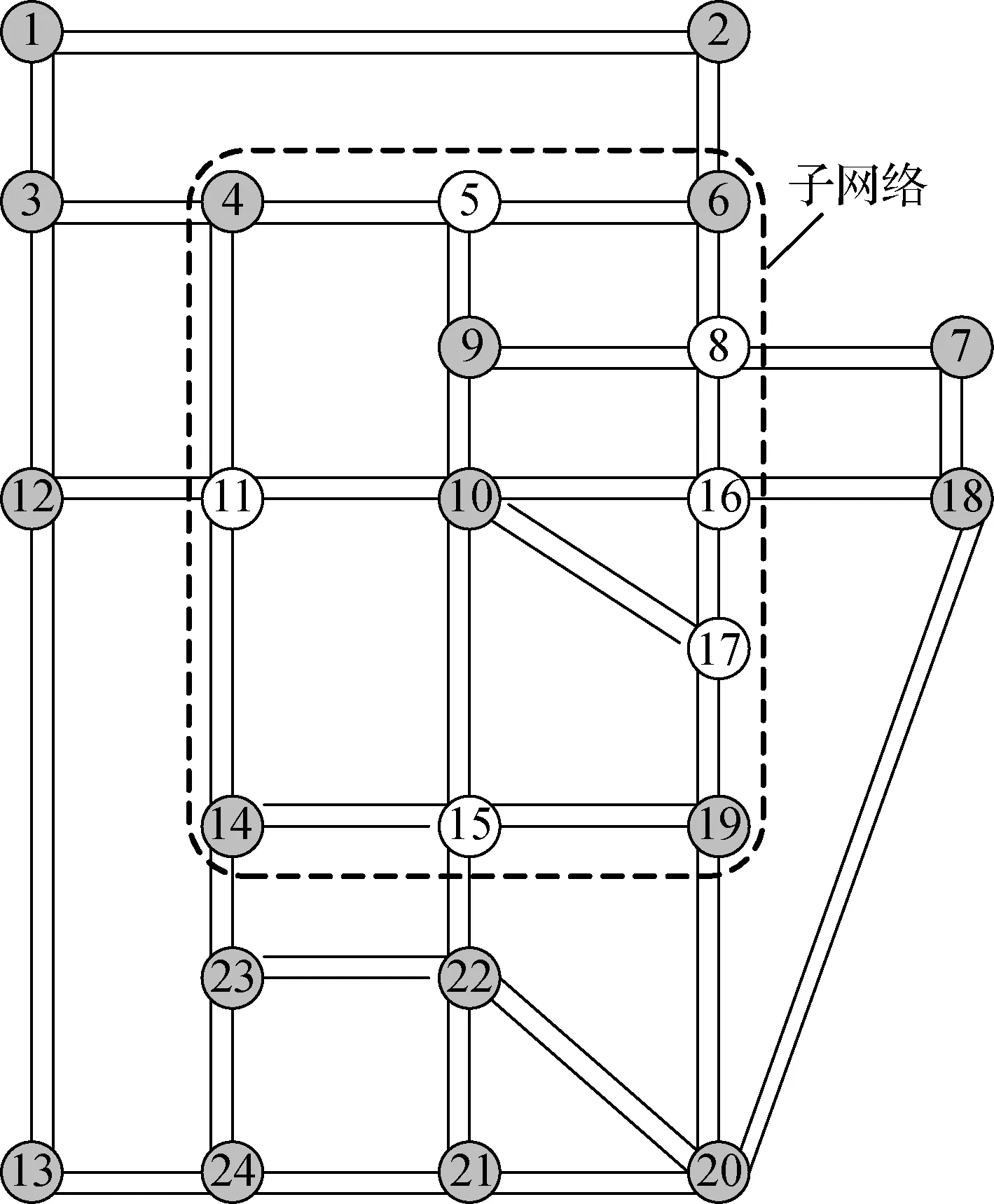
(a) Sioux Falls路网

(b) 子网络拓扑及边界流量

根据式(1)～(2),建立子网络OD需求估计模型.

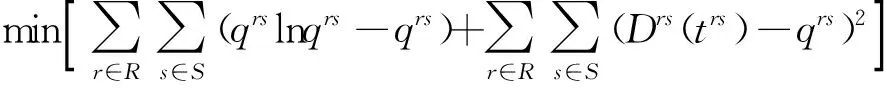
(4)

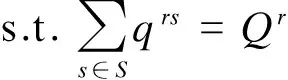
(5a)

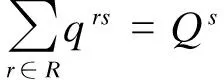
(5b)

qrs=0 ∀r=s∈{4,6,8,11,14,15,16,19}

(5c)

qrs=C∀r,s∈{4′,6′,9,10,14′,19′}

(5d)

首先将边界的OD点转换为非OD点和辅助OD点(见图2(b)),根据转换后的网络,式(5a)、(5b)给出了所有路网结点的总交通生成和吸引量,如点6的总发生量为3 533,总吸引量为3 538.边界点4,6,8,11,14,15,16和19与外部网络只有一条出弧和入弧相连,式(5c)显示这些点只对外部点产生吸引量与发生量,从式(5d)可知,点4′,6′,9,10,14′和19′之间的交通量与原网络保持一致.

由于基于全网络交通叠加的OD估计方法[4-5]和基于子网络外部网络简化[6-8]的 OD估计方法均考虑了子网络的外围,而基于子网络道路流量约束的 OD估计方法[9-10]和本文的OD估计方法都仅针对子网络本身,因而本文对后2种方法进行了比较.本文方法含有182个自变量72个有效约束,而基于子网络道路流量约束模型包含132个自变量和34个有效约束,因而本文建立的模型在约束与自变量数量比值上优于基于子网络道路流量约束模型,即本文建立的模型可得到更优的可行域范围.

然后对算法的收敛速度进行了测试,结果如图3所示.从图3(a)可看出,设计的启发式迭代算法达到1.0×10-4精度约需26 s;从图3(b)可看出,凸组合算法在迭代过程中有一些震荡现象.这表明设计的算法可很快收敛到所需精度.

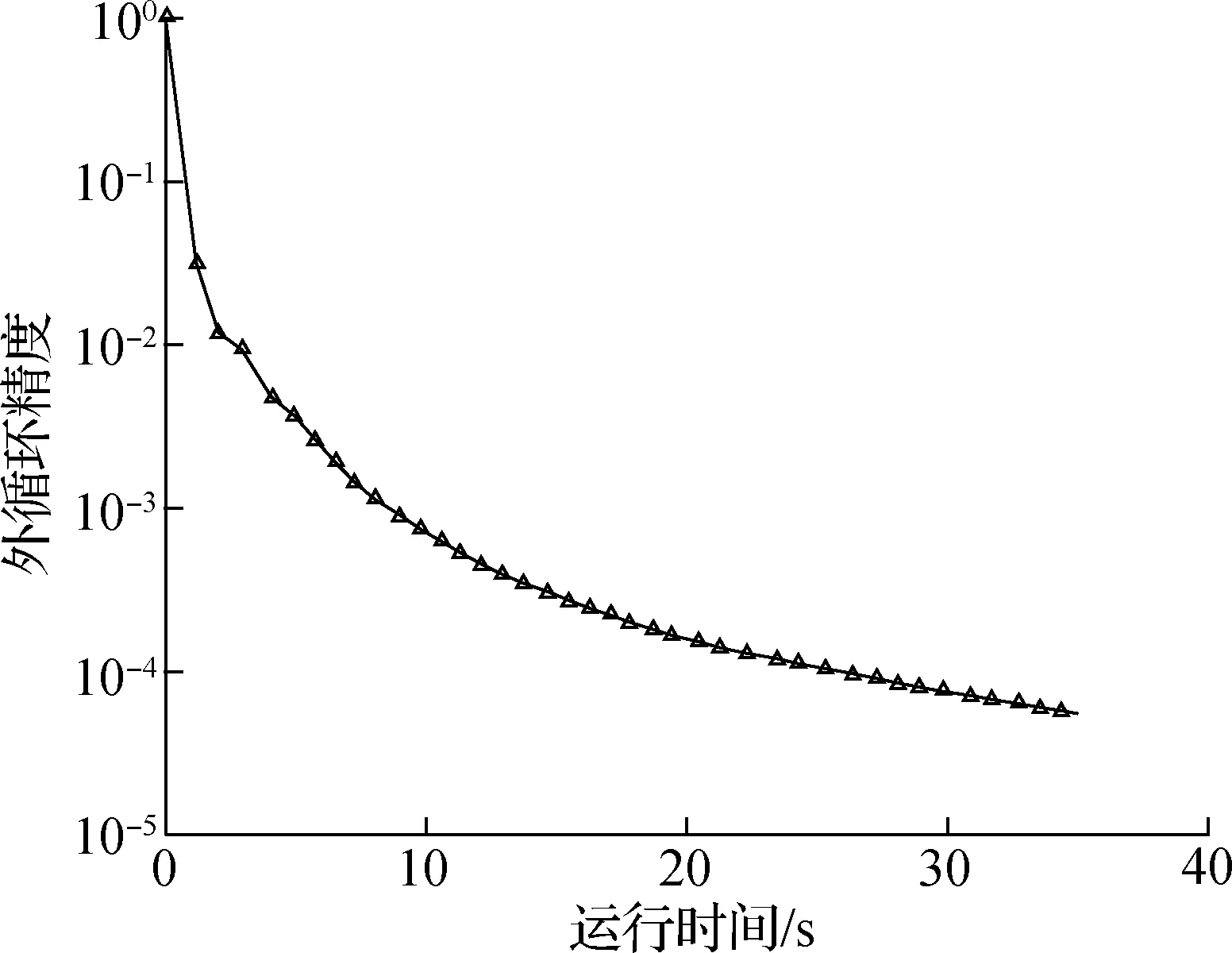
(a) 启发式迭代算法

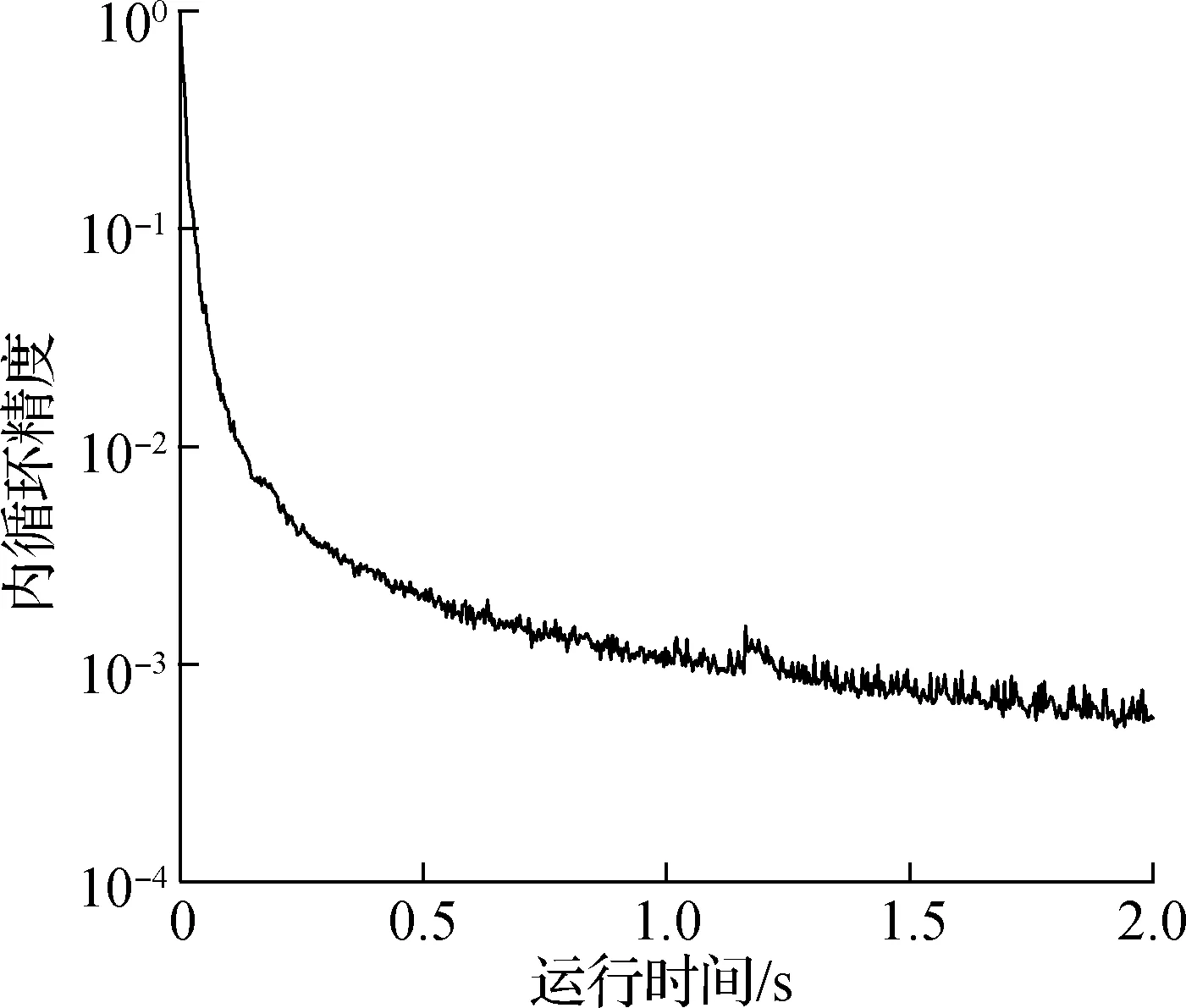
(b) 凸组合算法

为了更好地说明建立的子网络OD估计模型的应用性,分别对全网络OD和估计出的子网络OD进行用户均衡分配,并给出了路段流量的相对误差,如图4所示,图中e为相对误差.从图中可发现当不考虑弹性需求时,子网络中很多路段的相对误差较大(超过20%),而当考虑弹性需求时,评估的子网络OD分配的路段流量与原网络分配的路段流量非常接近.这表明运用本文设计的子网络OD需求估计模型对全网络进行简化是有效且实用的方法.

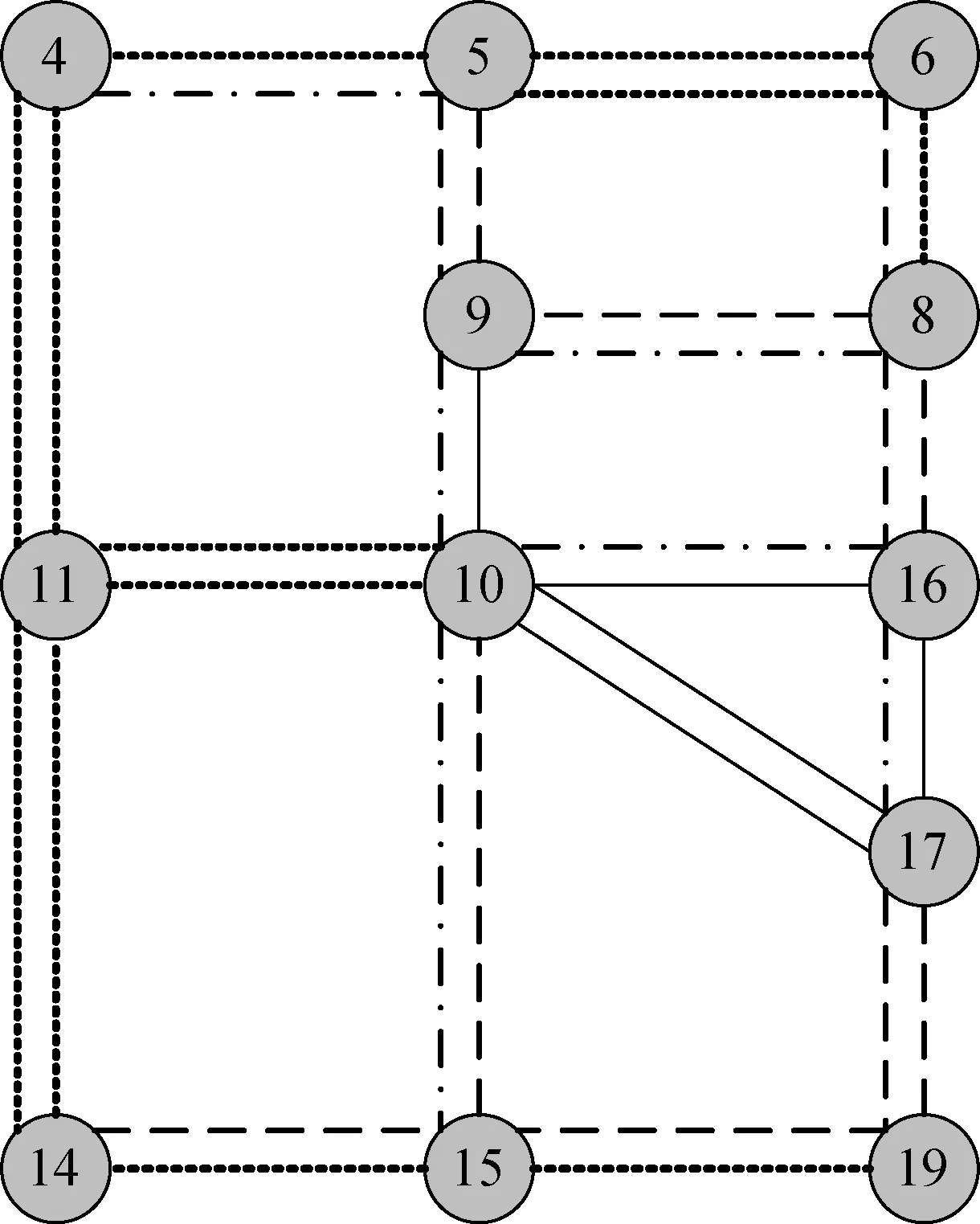
(a) 不考虑弹性需求

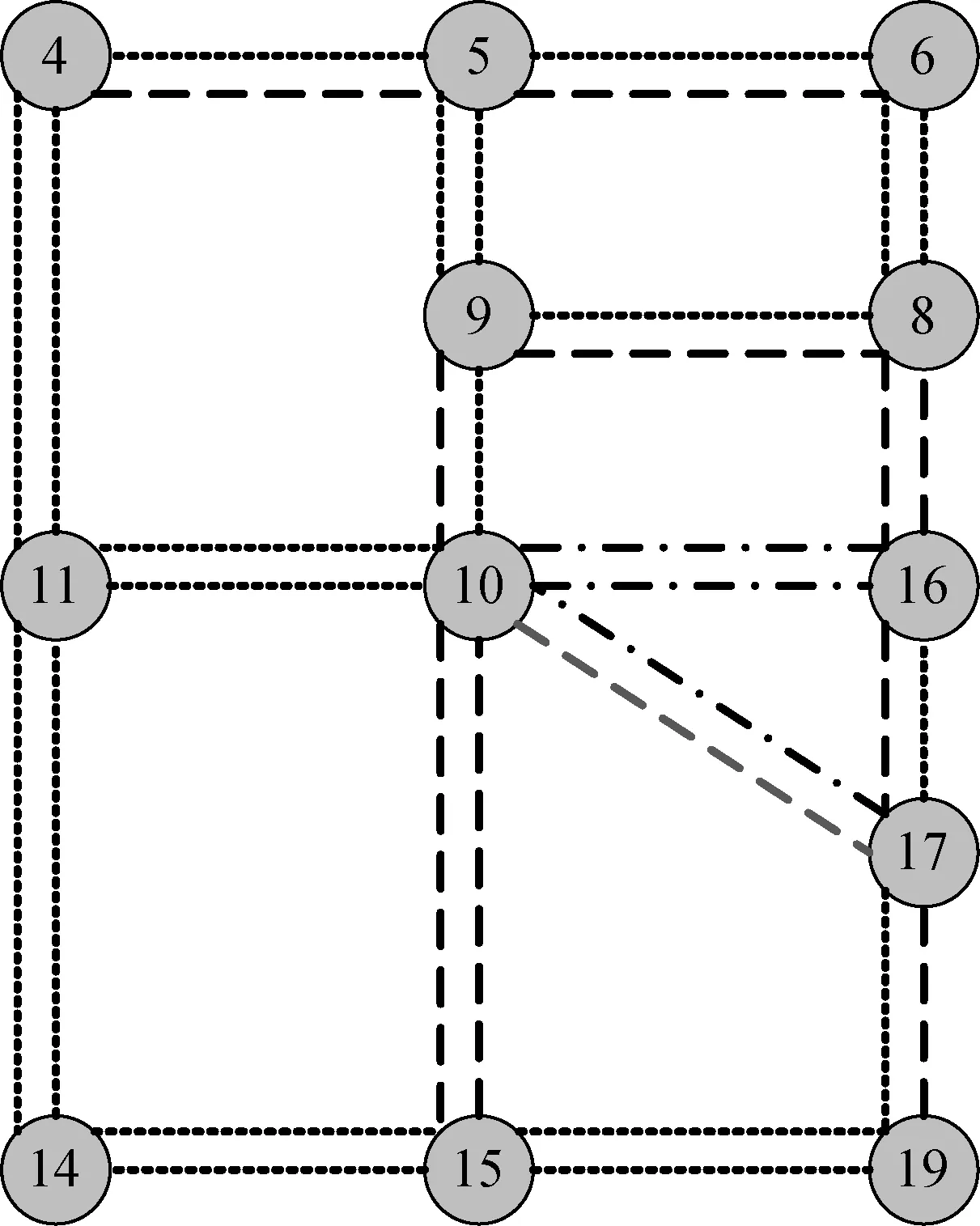
(b) 考虑弹性需求

4 结论

1) 基于子网络拓扑的OD需求估计模型对实际城市路网进行简化,进而在城市道路改造或者新建城市用地时,可以对周边交通进行重点研究与规划,减少了外围网络对子网络的干扰.

2) 设计的启发式迭代算法将复杂的原问题分解为OD估计和交通分配,运用凸组合算法求解交通需求,避免了使用复杂的模拟仿真方法求解建立的模型.

3) 算例还表明,考虑弹性需求的子网络OD估计模型可以反应外部网络变化对子网络的影响.考虑固定需求的子网络OD估计下部分路段流量误差大于20%,而考虑弹性需求的估计模型误差均在20%以内.

)

[1] Goodwin P, Noland R B. Building new roads really does create extra traffic: A response to Prakash et al.[J].AppliedEconomics, 2003,35(13): 1451-1457. DOI:10.1080/0003684032000089872.

[2] Millard-Ball A. Phantom trips: Overestimating the traffic impacts of new development [J].JournalofTransportandLandUse, 2015,8(1): 31-49. DOI:10.5198/jtlu.2015.384.

[3] 程琳.城市交通网络流理论[M].南京:东南大学出版社,2010:15-30.

[4] Haghani A E, Daskin M S. Network design application of an extraction algorithm for network aggregation [J].TransportationResearchRecord, 1983,944: 37-46.

[5] Zhou X, Erdogan S, Mahmassani H. Dynamic origin-destination trip demand estimation for subarea analysis[J].TransportationResearchRecord:JournaloftheTransportationResearchBoard, 2006,1964: 176-184. DOI:10.3141/1964-19.

[6] Boyles S D. Bush-based sensitivity analysis for approximating subnetwork diversion[J].TransportationResearchPartB:Methodological, 2012,46(1): 139-155. DOI:10.1016/j.trb.2011.09.004.

[7] Jafari E, Boyles S D. Improved bush-based methods for network contraction[J].TransportationResearchPartB:Methodological, 2016,83: 298-313. DOI:10.1016/j.trb.2015.11.014.

[8] Gemar M, Bringardner J, Boyles S, et al. Subnetwork analysis for dynamic traffic assignment models: Strategy for estimating demand at subnetwork boundaries [J].TransportationResearchRecord:JournaloftheTransportationResearchBoard, 2014,2466: 153-161.

[9] Xie C, Kockelman K, Waller S. Maximum entropy method for subnetwork origin-destination trip matrix estimation[J].TransportationResearchRecord:JournaloftheTransportationResearchBoard, 2010,2196: 111-119. DOI:10.3141/2196-12.

[10] Xie C, Kockelman K M, Waller S T. A maximum entropy-least squares estimator for elastic origin-destination trip matrix estimation [J].TransportationResearchPartB:Methodological, 2011,45(9): 1465-1482. DOI:10.1016/j.trb.2011.05.018.

[11] 张光澄.非线性最优化计算方法[M].北京:高等教育出版社,2005:261-291.

[12] 王炜,陆建.道路交通工程系统分析方法[M].北京:人民交通出版社,2011:55-82.

Subnetworkorigin-destinationmatrixestimationconsideringnetworktopology

Sun Chao Cheng Lin Luan Xin Tu Qiang Ma Jie

(School of Transportation, Southeast University, Nanjing 210096, China)

To design and evaluate the local transportation road network, the subnetwork origin-destination (OD) demand is estimated using the method of topology analysis. The nodes on the boundary of the subnetwork and inside the subnetwork are analyzed based on the subnetwork topology structure. The nodes on the boundary of the subnetwork, which connect with the outside of the subnetwork, generate or attract traffic flows; and the demands of the nodes inside the subnetwork are the same as those in the original full network. Then, the subnetwork OD matrix estimation model considering the subnetwork topology is established. This new model considers the maximum entropy and elasticity of OD demands in the objective function, and uses the OD demands as the constraints. The original problem is divided into solving the OD demand and road impedance, respectively. The heuristic iterative algorithm is designed to solve the established model, and the convex combination algorithm is developed to calculate the OD demand. The Sioux Falls network is used to illustrate the essential idea of the proposed model and the applicability of the proposed solution algorithm. The results show that the proposed model with elastic demand is superior to the OD estimation model with fixed demand in the terms of reliability and computational accuracy. The designed algorithm can rapidly convergence to the required accuracy, and the proposed model is an effective approach for simplifying the full network.

origin-destination matrix estimation; subnetwork analysis; topology structure; elastic demand; heuristic iterative algorithm

10.3969/j.issn.1001-0505.2017.06.026

U491

A

1001-0505(2017)06-1248-05

2017-02-20.

孙超(1990—),男,博士生;程琳(联系人),男,博士,教授,博士生导师,gist@seu.edu.cn.

国家自然科学基金资助项目(51578150,51378119)、东南大学优秀博士论文基金资助项目(YBJJ1679)、江苏省研究生创新基金资助项目(KYLX15_0150)、国家留学基金委资助项目.

孙超,程琳,栾鑫,等.基于网络拓扑的子网络OD需求估计[J].东南大学学报(自然科学版),2017,47(6):1248-1252.

10.3969/j.issn.1001-0505.2017.06.026.