围压条件下TBM边缘滚刀破岩模式

薛亚东 杨文亮 黄宏伟 张学强

(1同济大学地下建筑与工程系, 上海 200092)(2同济大学岩土及地下工程教育部重点实验室, 上海 200092)(3上海市城市建设设计研究总院(集团)有限公司, 上海 200125)(4山东天工岩土工程设备有限公司, 聊城 252000)

围压条件下TBM边缘滚刀破岩模式

薛亚东1,2杨文亮3黄宏伟1,2张学强4

(1同济大学地下建筑与工程系, 上海 200092)(2同济大学岩土及地下工程教育部重点实验室, 上海 200092)(3上海市城市建设设计研究总院(集团)有限公司, 上海 200125)(4山东天工岩土工程设备有限公司, 聊城 252000)

为了解边缘滚刀的破岩特性，对其破岩过程与机理开展了系统研究.建立了某深埋全断面岩石隧道掘进机(TBM)开挖隧道三维有限元模型，在掌子面过渡圆弧周边设置边缘滚刀破岩模型边界，导出边界上的围压数值并施加在颗粒流模型边界上.模型考虑5种围压模式，相位角为0°，30°，60°，90°时的岩石应力状态分别记为模式1～模式4，无围压状态记为模式5.结果表明：围压模式1中岩石双向应力和、双向应力比均最大，破岩比能最低；模式3中，岩石受到滚刀水平向力作用而近似处于双向等值应力状态，破岩比能最高；从模式1到模式3，有利破岩的竖向应力递减；从模式5到模式3，不利破岩的水平应力增加，导致模式3条件下刀具破岩效率最低；有围压模式的侧向力系数和滚刀切入率均高于无围压模式.

TBM;边缘滚刀;围压;破岩模式

TBM刀盘上安装有一定数量的盘形滚刀,盘形滚刀在TBM推力和扭矩的共同作用下绕刀盘主轴做圆周运动,根据滚刀在刀盘上位置的不同,可以分为中心滚刀、正面滚刀和边缘滚刀.其中正面滚刀数量明显占优,一般占滚刀数目的60%左右;正面滚刀平面与岩石掌子面垂直,破岩过程较为简单、明确.目前,绝大多数破岩过程研究集中在正面滚刀上[1-5].

边缘滚刀的破岩特性与正面滚刀有如下差异:① 边缘滚刀平面与TBM前进方向之间存在一个夹角,称为安装倾角,导致边缘滚刀所受侧向力较大;② 边缘滚刀安装在刀盘的过渡圆弧上,相邻边缘滚刀破岩形成的掌子面近似为弧面;③ 考虑到地应力的作用,正面滚刀临空掌子面的岩石大致呈双向受力状态,而弧面掌子面的岩石由于弧面拱效应的影响呈三向受力状态,对破岩过程有较大影响;④ 当TBM转弯时,边缘滚刀位于刀盘最外侧,作用力变化幅度较大,易造成滚刀失效[6-9].

根据秦岭隧道出口段TBM掘进5 621 m的施工数据资料,边缘滚刀平均寿命为248 m,大约是正面滚刀寿命的1/5;边缘滚刀的检测报废率为28.6%,大约为正面滚刀的4倍[10].

近年来国内外学者就边缘滚刀破岩过程逐步开展相关研究.张厚美[11]提出由于边缘滚刀两侧刀间距不同,导致破岩形成的破碎槽左右不对称,易引起边缘滚刀的偏磨,并已在秦岭隧道中得到验证.张照煌等[12]采用塑性理论推导证明了外倾安装的滚刀破岩比能较正面滚刀低,其结论对于评估边缘滚刀破岩效率具有参考意义.吴元[13]采用LS-DYNA分析滚刀三维运动,建立了边缘滚刀破岩能耗与安装倾角的关系,进而求得边缘滚刀最优安装倾角.Gharahbagh等[14]开发了一套盾构刀盘边缘刮刀磨损量的自动测量装置,为边缘滚刀磨损规律研究提供了手段.沈斌[15]开展了多因素敏感性分析,认为影响边缘滚刀破岩过程最主要的2个因素是边缘滚刀间倾角差和刀盘过渡圆弧半径.Huo 等[16]基于理论与试验,研究得出滚刀安装倾角对滚刀受力有显著影响.夏毅敏等[17]采用UDEC软件研究了刀刃角对于边缘滚刀破岩效率、破岩临界双向应力和裂纹长度的影响.Hassanpour等[18]统计了伊朗Karaj输水隧道南北两端2个TBM工程换刀情况,结果显示边缘滚刀磨损更为严重,换刀次数明显多于正面滚刀和中心滚刀.吴元等[19]采用正交试验设计方法,研究了不同刀刃角、刃宽、刀盘过渡圆弧半径和滚刀安装倾角情况下,边缘滚刀的破岩效率.

目前关于边缘滚刀的研究主要集中在优化边缘滚刀及刀盘设计参数上,文献[20]通过数值试验验证了围压对滚刀破岩过程有显著影响.国内外已有多条TBM施工隧道最大埋深超过1 000 m,在如此深埋的地层中施工,围压是必须要考虑的重要因素,特别是对边缘滚刀破岩机理的影响.

1 边缘滚刀破岩模型边界应力设定

边缘滚刀布置在TBM刀盘的过渡圆弧处,如图1所示.过渡圆弧区域岩石在曲面上易产生“岩石拱”效应,并且由于形状突变易导致应力集中现象,边缘滚刀与围岩相互作用应力状态较为复杂.

图1 TBM刀盘布置示意图

为获取边缘滚刀围岩区域的地层应力分布,以某深埋TBM隧道为例,建立如图2所示的三维有限元模型.模型尺寸为100 m×100 m×60 m,隧道直径8.0 m,埋深800 m(模型中隧道顶上覆岩层厚度65 m,通过压力边界模拟800 m埋深),掌子面过渡圆弧半径0.6 m,模型共计69 092个单元.考虑刀盘推力对掌子面产生的附加应力,以秦岭隧道TB880E型TBM为例,将2/3的额定推力均匀作用在掌子面上,经换算需要在掌子面上施加0.23MPa的均布压力.参考《公路隧道设计规范》以及实测数据,确定有限元计算模型输入参数取值,见表1.屈服判定采用摩尔库伦强度准则,模型底部边界采用固定约束,4个侧面采用约束法向位移,顶面设置自由应力边界.

图2 深埋TBM隧道有限元模型

表1 有限元模型输入参数

建立直角坐标系,如图3所示.坐标原点位于掌子面圆心,z轴沿隧道轴线出掌子面方向,y轴竖直向上,x轴水平向右.在直角坐标系基础上建立柱面坐标系,柱面坐标系原点及z轴与直角坐标系重合,r轴表示向外辐射方向,相位角θ为掌子面上从y轴正向沿顺时针方向到r轴所转过的角度.

图3 掌子面直角及柱面坐标系

取柱面坐标系的r-z平面,建立柱面坐标系下的边缘滚刀破岩模型,如图4所示.AC,OB,OD,AB四条边表示岩样的应力边界,并分别简记为1#,2#,3#,4#边界,其中AC=OD=0.4 m,AB=OB=1.2 m.由于z轴位于隧道轴线上,隧道半径为4.0 m,故该模型中r轴取值为3.2～4.4 m.

将2#边界和4#边界各分为6小段,每段长0.2 m,如图5所示. 2#边界和4#边界为应力伺服控制边界,记录2#和4#边界各小段的应力分布情况,将计算得到的各小段应力均值作为该小段边界的预设应力,以便控制颗粒流模拟中所施加围压的大小.1#边界和3#边界均为被动边界,颗粒流模拟时将不参与伺服控制.分别将0°,30°,60°,90°四种相位角时的岩石应力状态记为模式1、模式2、模式3、模式4,并将无围压状态记为模式5.各围压模式下依据有限元计算结果设置各段边界应力值,见表2.

图5 边界应力分布计算简图

围压模式2#墙预设应力/MPa4#墙预设应力/MPas21s22s23s24s25s26平均值s41s42s43s44s45s46平均值双向应力和/MPa双向应力比模式16.628.399.8710.299.728.438.895.739.8816.4020.9922.8322.8416.4525.341.85模式26.177.789.289.939.698.758.605.929.0914.1217.6518.9818.9814.1222.721.64模式35.246.518.079.219.679.488.035.277.089.6911.0411.4111.389.3117.341.16模式44.735.837.418.789.639.857.714.775.927.397.737.617.566.8314.540.89模式50 0 0 0 0 0 0 0 0 0 0 0 0 0 0

2 边缘滚刀破岩过程颗粒流模拟

建立岩石材料的颗粒流模型,颗粒接触采用 线性平行黏结模型.为了尽可能接近宏观岩石力学参数,采用控制变量法调整颗粒流模型微观参数,试算并标定出每种参数组合下岩样的宏观力学参数,反复调试直到颗粒流岩样模型宏观力学参数接近表1中的有限元模型参数.颗粒流模型的微观参数取值如表3所示.

依据图5的几何形状建立边缘滚刀破岩颗粒

表3 岩石材料颗粒流微观参数(平行黏结)

流模型,模拟岩样共计53 582个球单元.通过编制FISH函数,伺服控制2#边界和4#边界共计12段短墙的移动速度,当短墙的真实应力与预设应力差的绝对值之和小于等于1 MPa时,伺服控制程序结束(将所有墙速度设为0).

滚刀水平向右移动,切割速度为0.4 m/s,计算切深为6 mm.在每种围压模式下分别选取0°,15°,30°,45°四种滚刀倾角,共计20种工况进行颗粒流模拟.在模拟过程中记录滚刀水平作用力、竖直作用力、侵入深度、剪切裂纹数、张拉裂纹数、岩石开裂荷载、破碎区域面积、破碎区域最大宽度、破碎区域最大深度等信息.

颗粒流模型中的滚刀采用如下方式建立:首先在CAD软件中建立滚刀刀刃的外轮廓线,然后导入到颗粒流模型中,并将滚刀轮廓线设置为“墙”单元,最后在保证岩样位置不动的前提下通过设置滚刀移动方向、速度、距离等参数实现切割.滚刀的安装倾角通过旋转导入的CAD线框来实现,不同安装倾角滚刀均沿水平向右进行切割破岩.

3 试验结果分析

滚刀切入岩石后其垂向接触力近似线性增大,至某一极值后出现陡降,岩石发生初次破碎,将滚刀力峰值称为岩石开裂荷载,对应的切深称为开裂切深,达到初始破碎时滚刀所耗能量称为开裂能量.通过PFC软件自带的fragment命令得到岩石在滚刀作用下破碎区图像,采用Matlab软件编制程序,处理图像并计算破碎区域以及整张图片的像素点数,进而依据真实的模型尺寸计算得到破碎区域面积.拉裂纹和剪切裂纹数目由PFC软件FISH编程自动统计得到.

破岩比能最早由Teale于1965年提出,定义为破碎单位体积的岩石所消耗的能量[21],是衡量滚刀破岩效率的重要指标,本文中,破岩比能采用下式计算:

(1)

式中,sE为比能;W为滚刀做功;Fx为滚刀水平向作用力;p为切深;A为破碎区面积.

边缘滚刀的运动可分解为垂直于岩石表面的法向运动和平行于岩石表面的侧向运动,如图5所示,法向切深采用下式计算:

pn=pcosα

(2)

式中,pn为法向切深;α为滚刀安装倾角.

滚刀力的转换方程为

(3)

式中,Fy为滚刀竖直向作用力;Fn为滚刀法向作用力;Ft为滚刀侧向作用力.

3.1 不同围压模式下的耗能及比能

统计4种安装倾角的破岩耗能、开裂耗能和比能的平均值,并按围压模式进行汇总,如图6所示.可以看出,破岩耗能、开裂耗能以及破岩比能变化规律类似,均在模式3中达到最高.对比滚刀破岩前后2#墙各短墙的应力变化,发现滚刀侵入岩石引起的2#墙水平附加应力大小为1～2 MPa,而2#墙平均应力值较4#墙约小1.3 MPa,使得模式3中的真实双向应力比接近1,岩石近似处于双向等值应力状态,岩石强度得到提升,故破岩耗能、开裂耗能和比能均最高.

图6 各围压模式的耗能及比能

在模式1中,破岩耗能、开裂耗能以及比能均最低,这是因为模式1的双向应力和最大,并且双向应力比也最大,在岩石破碎前已发生较大的变形并且吸收了较多的应变能,故模式1中的耗能以及比能在5种模式中最小.模式2、模式4、模式5中破岩耗能、开裂耗能以及比能较为接近,这反映了模式2和模式4中虽然存在围压,但围压对滚刀破岩能耗的影响较小,与无围压模式类似.

3.2 不同围压模式下的裂纹扩展

围压状态会影响裂纹的扩展过程,夏毅敏等[22]研究表明:随着围压增加,滚刀破岩引起的裂纹方向由垂直岩石表面向平行岩石表面方向转变;当围压增加到20 MPa时,岩石内部裂纹沿2个方向的扩展均受到抑制.统计汇总各围压模式下4种安装倾角的破碎区域深宽平均值,结果见图7.从模式1至模式4,4#墙与2#墙的双向应力比降低,导致破碎主裂纹与岩石自由面夹角增大,即破碎区域深宽比数值增大.模式5中考虑到滚刀破岩过程会对2#墙产生附加应力,由于4#墙应力远低于2#墙应力,故可以认为模式5的实际双向应力比为0,由此可见,破碎区域的深宽比与双向应力比具有很强的负相关性.李博[23]认为围压对破岩过程的影响突出反映在长裂缝与岩石自由面的夹角上,其结论与本文研究结果相吻合.

图7 各围压模式破碎区几何特征

当双向应力比大于1时,竖向应力起主导作用,会抑制水平向裂纹而促进竖向裂纹的发展;当双向应力比小于1时,水平应力起主导作用,会抑制竖向裂纹而促进水平向裂纹的发展.滚刀安装倾角一般小于45°,在图5所示的破岩过程中,竖向裂纹延伸到岩石自由面最终形成有效破碎面积,而水平向裂纹向岩石内部延展,很难形成有效破碎,故竖向应力促进破岩,水平向应力抑制破岩.从模式1到模式3,竖向应力递减,促进作用减弱;从模式5到模式3,水平应力在增加,抑制作用增强,因而模式3破岩效率最低,3.1节中模式3的破岩耗能、开裂耗能、比能均最高证明了此结论.将不同围压模式下开裂荷载与裂纹数目进行统计汇总,见表4.从表中看出,模式3的开裂荷载、法向开裂荷载是所有模式中最高的,模式2和模式4次之,模式

表4 不同围压模式下裂纹扩展统计

1和模式5最低,也证明了上述分析的正确性.

裂纹数目可以反映岩石破碎程度,从表4中数据可知,双向应力和越大,裂纹数越少,没有围压情况下的裂纹数最多,反映出围压对裂纹扩展整体上起到抑制作用.裂纹数目除与双向应力和有关外,也与双向应力比有关,当双向应力比接近1时,岩石处于双向等值压缩状态,体积压缩变形的比例增大,形状改变的比例降低,而体积压缩变形(3个维度的压应变较为接近,物体被近似等形状压缩)过程产生的裂纹数目远低于形状改变过程(3个维度的压应变有较大差异,形状发生明显改变),因此裂纹数目有所降低,故而模式3中裂纹数目比模式2少.

岩石在滚刀作用下的破坏以受拉破坏为主,同时伴有剪切破坏,剪切破坏主要集中在与滚刀接触的岩石压密区中,由表4可知,破岩过程中拉裂纹比例超过90%.无围压情况下的拉裂纹比例最高,有围压条件下,模式3拉裂纹比例最低,原因如前所述.

3.3 不同围压模式下的滚刀力变化规律

定义侧向力系数为边缘滚刀侧向力均值与法向力均值的比值,4种安装倾角的侧向力系数平均值在不同围压模式中的变化情况如图8所示.侧向力系数与4#墙产生的竖向应力有较强的相关性,从模式1至模式5,竖向应力递减,侧向力系数也大致呈现递减趋势.侧向力有助于破岩,同时容易引起滚刀轴承破坏和刀圈挡圈脱落,以及刀圈左右非对称磨损,图9为某TBM现场边缘滚刀非对称磨损照片.

图8 各围压模式的侧向力系数

将切入率定义为滚刀侵入岩石至其初始开裂过程中单位法向切深对应的滚刀法向力.5种围压模式下的滚刀切入率见图10.可看出,模式1～模式4的切入率均高于模式5.夏毅敏等[24]研究表明:地应力的存在可使法向力与滚动力增加70%以上,与本文研究规律吻合.在TBM选型时,应考虑地应力因素,优化刀盘额定推力与刀具布置.

图9 边缘滚刀左右非对称磨损

图10 不同围压模式的切入率

3.4 安装倾角对边缘过渡破岩过程的影响

以围压模式2为例,考虑4种滚刀安装倾角,滚刀作用下岩石破碎情况如图11所示,图中滚刀运动方向均为水平向右,按照预设切割速度侵入岩石.

(a) 0°(b) 15°

(c) 30°(d) 45°

滚刀侧向力系数如图12所示,侧向力系数总体上随安装倾角的增大而增大,但在30°附近出现降低.图13所示为围压模式2的滚刀力变化情况.

边缘滚刀侧向力系数远高于正面滚刀,根本原因在于滚刀前进方向(沿隧道轴向的前进方向)与滚刀平面不平行,当刀盘推进时,边缘滚刀沿空间螺旋线前进,在隧道轴向上边缘滚刀对岩层有类似“刮擦”的相对滑动.45°安装角时的侧向力最高,边缘滚刀非正常磨损和失效情况最为严重,易导致“卡盾”事故.秦岭铁路隧道TBM最外侧同时设置3把边缘滚刀,一方面为了更好地“保径”,另一方面为了降低刀具负担,提高边缘滚刀的可靠性.另外,30°倾角附近的边缘滚刀侧向力方向会发生反转,冲击荷载易造成滚刀轴承、密封圈和挡圈的损坏.

图12 不同滚刀倾角的侧向力系数

(a) 15°

(b) 30°

(c) 45°

4 讨论

滚刀破岩过程是一个三维空间问题,用二维颗粒流软件模拟存在一定的局限性,尤其是滚刀力的绝对数值与真实滚刀力可能存在较大差异,但对于破岩过程和机理的研究仍具有优越性.

与滚刀直接接触的岩石区域应力极高,被压密成核,颗粒流模拟中能够观察到密实核的存在,滚刀应力作用到密实核后,再通过密实核向四周传递,形成辐射状应力流线(见图14(a)).密实核宽度与刀圈刃宽相当,根据布辛奈斯克解的结论,滚刀法向力的附加应力在岩石深度方向快速衰减,故密实核深度有限,从线性切割试验过程中观察到的现象来看(试验采用直径483 mm的近似常截面平刃滚刀,刀刃宽度约1.8 cm),密实核深度约为宽度的1/2(见图14(b)).

(a) PFC模拟中的密实核(b) 试验过程中的密实核

通过在有限元软件后处理模块中设置场输出路径点,得到图4中r=4.2 m时z坐标轴上5个点的σz沿相位角的分布,见图15(a);同时记录z=0.2 m时r坐标轴上5个点的σr沿相位角的分布,见图15(b).应力沿相位角分布具有显著的对称性和周期性,说明本文取相位角θ∈[0°,90°]区间是合理可行的.

围压模式随相位角的改变而周期性变化,随着刀盘的转动,某把边缘滚刀会往复切割处于不同围压模式的岩石,滚刀破岩过程中各项参数也会发生周期性的变化,会引起滚刀及TBM诸多问题.例如,初始开裂荷载的不同将引起刀盘的震动;破碎区深度不同,将导致某些位置的滚刀因作用力较小从而造成滚刀偏磨,某些位置的滚刀因作用力陡增导致轴承损坏;不同刀盘相位角的侧向力系数不同,将导致滚刀侧向震动明显,引起滚刀密封和挡圈失效.

(a) σz应力的空间分布

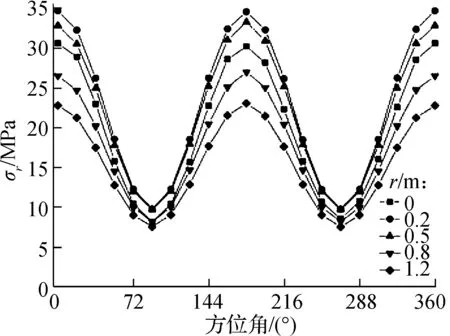
(b) σr应力的空间分布

针对以上问题,结合围压模式对边缘滚刀破岩过程影响的研究成果,针对性地提出相应工程控制措施:根据不同倾角的边缘滚刀的初始破岩荷载,合理设置各边缘滚刀在刀盘上的相位角,将边缘滚刀引起的不平衡力矩降至最低;通过合理调整各边缘滚刀先后破岩次序以及调整某些边缘滚刀安装高度,尽量减小相邻滚刀破碎区域深度的差异;边缘滚刀所受侧向力较大,且侧向力系数随着围压模式的改变而变化,建议提高边缘滚刀抗侧向力设计强度.

5 结论

1) 边缘滚刀破岩过程较正面滚刀和中心滚刀更复杂,原因在于其前进方向与滚刀平面斜交,在侵入破岩过程中发生侧向的相对运动.本文基于800 m埋深、8 m直径,岩层完整性较好的TBM隧道工程开展研究,提出了5种围压模式,研究不同围压模式对边缘滚刀破岩过程的影响规律,成果对于考虑地应力状态进行TBM选型与刀盘刀具布置设计具有参考价值.

2) 围压模式对破岩比能有明显的影响,在围压模式3中,岩石大致呈双向等值应力状态,破岩比能在所有模式中最高;模式1双向应力和与双向应力比均最大,岩石初始应变能较高,破岩比能在所有模式中最低.从模式1到模式3,竖向应力递减,促进作用在减弱;从模式5到模式3,水平应力增加,抑制作用逐渐增强,导致模式3破岩效率最低.随着双向应力比的降低,破碎区域的深宽比逐渐增大.

3) 有围压模式的侧向力系数高于无围压模式,边缘滚刀在较大侧向力作用下更容易损坏和失效;45°倾角时侧向力系数最高,侧向力最大,磨损也最严重;30°倾角时滚刀侧向力在破岩过程中会发生方向反转,加剧刀盘振动且易造成滚刀失效.

)

[1] Wijk G. A model of tunnel boring machine performance[J].GeotechnicalandGeologicalEngineering, 1992,10(1): 19-40. DOI:10.1007/bf00881 969.

[2] Gertsch R, Gertsch L, Rostami J. Disc cutting tests in Colorado Red Granite: Implications for TBM performance prediction[J].InternationalJournalofRockMechanicsandMiningSciences, 2007,44(2): 238-246. DOI:10.1016/j.ijrmms.2006.07.007.

[3] Moon T,Oh J. Study of optimal rock-cutting conditions for hard rock TBM using the discrete element method[J].RockMechanicsandRockEngineering, 2012,45(5): 837-849. DOI:10.1007/s00603-011-0180-3.

[4] 谭青,易念恩,夏毅敏,等.TBM滚刀破岩动态特性与最优刀间距研究[J].岩石力学与工程学报,2012,31(12):2453-2464. DOI:10.3969/j.issn.1000-6915.2012.12.009.

Tan Qing, Yi Nianen, Xia Yimin, et al. Research on rock dynamic fragmentation characteristics by TBM cutters and cutter spacing optimization[J].ChineseJournalofRockMechanicsandEngineering, 2012,31(12): 2453-2464. DOI:10.3969/j.issn.1000-6915.2012.12.009.(in Chinese)

[5] 龚秋明,何冠文,赵晓豹,等.掘进机刀盘滚刀间距对北山花岗岩破岩效率的影响实验研究[J].岩土工程学报,2015,37(1):54-60. DOI:10.11779/CJGE201501005.

Gong Qiuming, He Guanwen, Zhao Xiaobao, et al. Influence of different cutter spacings on rock fragmentation efficiency of Beishan granite by TBM[J].ChineseJournalofGeotechnicalEngineering, 2015,37(1): 54-60. DOI:10.11779/CJGE201501005.(in Chinese)

[6] Innaurato N, Oggeri C, Oreste P P, et al. Experimental and numerical studies on rock breaking with TBM tools under high stress confinement[J].RockMechanicsandRockEngineering, 2007,40(5): 429-451. DOI:10.1007/s00603-006-0109-4.

[7] Gong Q M, Zhao J. Development of a rock mass characteristics model for TBM penetration rate prediction[J].InternationalJournalofRockMechanicsandMiningSciences, 2009,46(1): 8-18. DOI:10.1016/j.ijrmms.2008.03.003.

[8] Espallargas N, Jakobsen P D, Langmaack L, et al. Influence of corrosion on the abrasion of cutter steels used in TBM tunnelling[J].RockMechanicsandRockEngineering, 2015,48(1): 261-275. DOI:10.1007/s00603-014-0552-6.

[9] 万治昌,沙明元,周雁领.盘形滚刀的使用与研究(2)——TB880E型掘进机在秦岭隧道施工中的应用[J].现代隧道技术,2002,39(6):1-12. DOI:10.3969/j.issn.1009-6582.2002.06.001.

Wan Zhichang, Sha Mingyuan, Zhou Yanling. Study on disk cutters for hard rock—application of TB880E TBM in Qinling Tunnel [J].ModernTunnellingTechnology, 2002,39(6): 1-12. DOI:10.3969/j.issn.1009-6582.2002.06.001.(in Chinese)

[10] 万治昌,沙明元,周雁领.盘形滚刀的使用与研究(1)——TB880E型掘进机在秦岭隧道施工中的应用[J].现代隧道技术,2002,39(5):1-11. DOI:10.3969/j.issn.1009-6582.2002.05.001.

Wan Zhichang, Sha Mingyuan, Zhou Yanling. Study on disk cutters for hard rock—application of TB880E TBM in Qinling Tunnel[J].ModernTunnellingTechnology, 2002,39(5): 1-11. DOI:10.3969/j.issn.1009-6582.2002.05.001. (in Chinese)

[11] 张厚美.TBM的掘进性能数值仿真研究[J].隧道建设,2006,26(z2):1-7. DOI:10.3969/j.issn.1672-741X.2006.z2.001.

Zhang Houmei. Study on numerical simulations of performance of tunnel boring machines TBM[J].TunnelConstruction, 2006,26(z2): 1-7. DOI:10.3969/j.issn.1672-741X.2006.z2.001.(in Chinese)

[12] 张照煌,户秀妹,孟亮,等.盘形滚刀破岩效能理论分析[J].应用基础与工程科学学报,2012,20(z1):199-206. DOI:10.3969/j.issn.1005-0930.2012.s1.021.

Zhang Zhaohuang, Hu Xiumei, Meng Liang, et al. Theoretical analysis of efficiency of rock breaking by disc cutters[J].JournalofBasicScienceandEngineering, 2012,20(z1): 199-206. DOI:10.3969/j.issn.1005-0930.2012.s1.021.(in Chinese)

[13] 吴元.TBM边缘滚刀破岩特性及其布置研究[D].长沙:中南大学机电工程学院,2013.

[14] Gharahbagh E A, Mooney M A, Frank G, et al. Periodic inspection of gauge cutter wear on EPB TBMs using cone penetration testing[J].TunnellingandUndergroundSpaceTechnology, 2013,38: 279-286. DOI:10.1016/j.tust.2013.07.013.

[15] 沈斌.TBM边缘滚刀组合优化布置研究[D].长沙:中南大学机电工程学院,2014.

[16] Huo J, Wang W, Sun W, et al. The multi-stage rock fragmentation load prediction model of tunnel boring machine cutter group based on dense core theory[J].TheInternationalJournalofAdvancedManufacturingTechnology, 2017,90(1): 277-289. DOI:10.1007/s00170-016-9375-9.

[17] 夏毅敏,吴元,郭金成,等.TBM边缘滚刀破岩机理的数值研究[J].煤炭学报,2014,39(1):172-178. DOI:10.13225/j.cnki.jccs.2013.0177.

Xia Yimin, Wu Yuan, Guo Jincheng, et al. Numerical simulation of rock-breaking mechanism by gage disc cutter of TBM[J].JournalofChinaCoalSociety, 2014,39(1): 172-178. DOI:10.13225/j.cnki.jccs.2013.0177.(in Chinese)

[18] Hassanpour J, Rostami J, Azali S T, et al. Introduction of an empirical TBM cutter wear prediction model for pyroclastic and mafic igneous rocks; a case history of Karaj water conveyance tunnel, Iran[J].TunnellingandUndergroundSpaceTechnology, 2014,43: 222-231. DOI:10.1016/j.tust.2014.05.007.

[19] 吴元,夏毅敏,郭金成,等.TBM边缘滚刀关键参数对破岩效率影响规律研究[J].现代隧道技术,2015,52(1):119-126. DOI:10.13807/j.cnki.mtt.2015.01.017.

Wu Yuan, Xia Yimin, Guo Jincheng, et al. Influence of key parameters of a TBM gauge disc cutter on rock-breaking efficiency[J].ModernTunnellingTechnology, 2015,52(1): 119-126. DOI:10.13807/j.cnki.mtt.2015.01.017.(in Chinese)

[20] Ma H, Yin L, Ji H. Numerical study of the effect of confining stress on rock fragmentation by TBM cutters[J].InternationalJournalofRockMechanicsandMiningSciences, 2011,48(6): 1021-1033. DOI:10.1016/j.ijrmms.2011.05.002.

[21] Teale R. The concept of specific energy in rock drilling[J].InternationalJournalofRockMechanicsandMiningSciences&GeomechanicsAbstracts, 1965,2(1): 57-73. DOI:10.1016/0148-9062(65)90022-7.

[22] 夏毅敏,张旭辉,谭青,等.不同围压下刀宽对滚刀破岩特性的影响规律[J].应用基础与工程科学学报,2017,25(3):636-645. DOI:10.16058/j.issn.1005-0930.2017.03.019.

Xia Yimin, Zhang Xuhui, Tan Qing, et al. Influence of rock breaking characteristics with disc cutter width under different confining pressure[J].JournalofBasicScienceandEngineering, 2017,25(3): 636-645. DOI:10.16058/j.issn.1005-0930.2017.03.019. (in Chinese)

[23] 李博.滚刀破岩过程的离散元模拟及试验研究[D].上海:同济大学土木工程学院,2013.

[24] 夏毅敏,吴才章,顾健健.不同地应力下TBM盘形滚刀破岩特性[J].中南大学学报(自然科学版),2016,47(2):450-458. DOI:10.11817/j.issn.1672-7207.2016.02.014.

Xia Yimin, Wu Caizhang, Gu Jianjian, et al. Mechanical characteristics of TBM disc cutter under the initial stress[J].JournalofCentralSouthUniversity(ScienceandTechnology), 2016,47(2): 450-458. DOI:10.11817/j.issn.1672-7207.2016.02.014.(in Chinese)

CuttingrockmodesofTBMgaugecuttersunderconfiningpressures

Xue Yadong1,2Yang Wenliang3Huang Hongwei1,2Zhang Xueqiang4

(1Department of Geotechnical Engineering, Tongii University, Shanghai 200092, China) (2Key Laboratory of Geotechnical and Underground Engineering of Ministry of Education, Tongji University, Shanghai 200092, China) (3Shanghai Urban Construction Design & Research Institute (Group) Co., Ltd, Shanghai 200125, China) (4Shandong Techgong Geotechnical Engineering Equipment Co., Ltd, Liaocheng 252000, China)

To acknowledge the rock breaking characteristics of the gauge cutters, systematic research on their rock breaking process and mechanism was carried out. A 3D finite element model of a deep-buried full-face rock tunnel boring machine (TBM) was established and calculated to obtain the geo-stress distribution of gauge cutter working area. Then, the corresponding pressure was applied on the particle flow code models boundaries. Five confining pressure models were considered. The rock stress states at phase angles 0°, 30°, 60°, and 90° were denoted as mode 1 to mode 4, and no confined pressure was denoted as mode 5. The numerical simulation results show that the sum of biaxial stress and its ratio of mode 1 are the largest among all modes. The specific energy of mode 1 is the lowest. In mode 3, the rock is subjected to the horizontal force of the cutters and is approximately in the bidirectional equivalent stress state. It has the highest specific energy. From mode 1 to mode 3, the vertical stress, which can promote rock fragmentation, is decreasing; from mode 5 to mode 3, the horizontal stress, which can suppress rock fragmentation, is increasing. Thus, the cutting efficiency of model 3 is the lowest. The results also show that the side force coefficients and cutting rates of cutters in the confining pressure modes are higher than those in the none-confining pressure mode.

TBM (tunnel boring machine); gauge cutter; confining pressure; cutting rock mode

10.3969/j.issn.1001-0505.2017.06.025

U452

A

1001-0505(2017)06-1239-09

2017-04-16.

薛亚东(1971—)，男，博士，副教授，博士生导师，yadongxue@126.com.

国家自然科学基金资助项目(41072206)、中央高校基本科研业务费专项资金资助项目(0200219209).

薛亚东,杨文亮,黄宏伟,等.围压条件下TBM边缘滚刀破岩模式[J].东南大学学报(自然科学版),2017,47(6):1239-1247.

10.3969/j.issn.1001-0505.2017.06.025.