基于双幂次趋近律火炮链传动药仓自适应控制

岳才成 钱林方 陈龙淼 田灵飞 杨会东

(1南京理工大学机械工程学院, 南京 210094)(2北方自动化技术研究所, 太原 030006)

基于双幂次趋近律火炮链传动药仓自适应控制

岳才成1钱林方1陈龙淼1田灵飞1杨会东2

(1南京理工大学机械工程学院, 南京 210094)(2北方自动化技术研究所, 太原 030006)

针对火炮链传动药仓在运动过程中存在负载非线性变化、抖振、参数不确定、非线性摩擦等问题，提出了一种自适应滑模控制策略.通过对系统等效转动惯量、扰动力矩等参数采取自适应估计,缓解了参数不确定性对模型的影响,使系统数学模型更加准确.采用新型双幂次趋近律降低切换过程中系统的抖振现象,并对趋近参数进行自适应在线选取,进一步提高了趋近过程和切换过程的鲁棒性.系统在不同负载下进行试验验证,结果表明,在该控制策略下，空载、半载、满载的链传动药仓均具有较好的稳定性和较高的控制精度，能够保证电机输出轴动态误差小于2.5 rad,稳定误差小于0.8 rad.

火炮链传动药仓;抖振;自适应控制;双幂次趋近律

火炮链传动药仓是自行火炮的核心组成部分,系统主要由药仓架体、储药机构、传动机构等组成,其中传动机构由交流同步伺服电机、减速机构、齿轮、链条等构成.运动过程中,交流同步伺服电机带动链条等中间机构,实现储药机构从任意位置运动到规定位置.为保证火炮药仓能够正常工作,要求机构具有较高的定位精度和较小的动态误差.

火炮链传动药仓的核心机构是传动机构.链传动机构被广泛运用在机械传动装置中,具有装调简单、可靠性高、效率高、持久性好等优点[1].但链传动过程中存在啮合冲击、振动、噪声、非线性摩擦等问题.邹权等[2]选用自适应模糊滑模控制方式对系统不确定参数进行处理.该方法有效减小了模型参数不确定性和外部扰动对伺服系统运动的影响,改善了运动状态,获得了较高的控制精度.针对被控对象具有非线性及参数不确定的问题,文献[3]提出采用自适应和模糊相结合的滑模控制方法.该方法完成了对双电机耦合驱动履带车辆的转向控制,实现了车辆的快速稳定控制.文献[4-7]对具有非线性、外部干扰的对象提出了以自适应控制为基础的控制策略，保证系统运动过程的跟踪误差在有效时间内收敛,增强了系统的鲁棒性能.

滑模变结构控制虽被广泛使用,但其切换特性会导致抖振发生.近年来,众多学者针对如何降低抖振进行了深入研究,提出了很多解决方案.高为炳[8]提出了应用趋近律的变结构控制方法,这种方法有效地降低了系统的抖振,提高了系统运动的品质.但是,传统趋近律缺点较为明显,如:等速趋近律在保证趋近速度时会引起较大的抖振.因此,该方法研究的重点是保证趋近过程和切换过程的品质,同时提高控制的时效性.周涛[9]利用特殊幂次函数和反双曲正弦函数设计了一种趋近律,并通过对二阶系统的仿真实验证明,提出的控制策略有效削弱了控制输入信号的高频震颤现象.文献[10]基于一种反正切形式的切换趋近律,设计了滑模控制方法,并将其应用于离散时间滑模控制系统中.仿真结果表明,系统获得了比较理想的跟踪性能,也能保证系统快速收敛至稳定状态.文献[11-13]提出了几种改进的趋近律,在仿真实验中均验证了算法的有效性,一定程度上削弱了运动过程中的抖振.

考虑到链传动药仓具有参数不确定、负载非线性变化和定位要求较高等特点，所以,该对象的控制必须保证运动过程平稳，具有较小的跟踪误差、较高的控制精度以及抖振控制在合理范围内.以上文献中提到的算法多数只进行了仿真分析,却很少有相关试验研究.本文根据研究现状和链传动药仓的自身特点,采用了双幂次趋近律对控制对象加以控制.选用链传动药仓台架进行试验验证分析,分析跟踪误差和输出控制电流的状态,验证提出算法的有效性.

1 链传动药仓动力学方程

药仓传动机构中的核心器件为交流同步伺服电机.选取d轴电流id=0的控制方法,得到电机的电磁转矩为

Te=p[ψiq+(Ld-Lq)idiq]=pψiq

(1)

式中,Te为电磁转矩;iq,id为q轴、d轴定子电流;Ld,Lq为定子绕组自感;ψ为磁链;p为电机的极对数.

取k=pψ为电机转矩常数,k>0;并令q轴电流iq=u,u为控制器的输出值，即Te=ku.将火炮链传动药仓动力学方程定义为

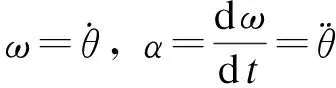
ku=Jα+Bω+ΔT

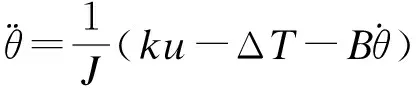
(2)

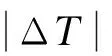
通过对q轴电流u的控制,实现药仓的位置运动,通过监测电机输出轴的速度和位置信息,完成对运动过程控制精度和控制性能的评估,验证算法的控制效果.

2 控制器设计

本文选取链传动药仓的位置误差为

e=θd-θ

(3)

式中,θd为转子理论角位置.设计PID型滑模函数为

(4)

式中,s为滑模函数;kp,ki,kd分别为滑模函数的比例、积分、微分系数.

本文设计一种新型的双幂次趋近律，即

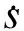
(5)

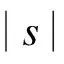
由式(4)和(5)可知

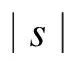
(6)

将式(2)代入式(6)得到

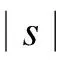
(7)

取k=1 N·m/A,链传动药仓的控制器设计为

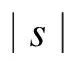
(8)

在运动过程中系统转动惯量、阻尼参数都会发生非线性的变化,选取固定值的方法显然影响控制器的准确性.考虑到运动过程中负载变化会对扰动力矩产生影响,本文对J,B,ΔT采用自适应的方式,在线估计运动过程中任意时刻的参数值.同时为了降低抖振,将控制器中的符号函数sgn(s)替换为饱和函数sat(s),饱和函数定义为

(9)

式中,Δ为待设定的边界层参数.综上,控制器改进为

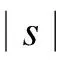
(10)

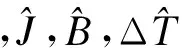
选取自适应律为

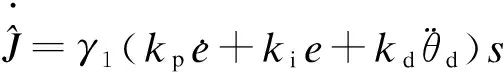
(11)

式中,γ1,γ2,γ3为自适应参量.

定理1若选取自适应律式(11),并采用式(10)的控制律,则被控系统能够保证在有限时间内收敛.

证明设计李雅普诺夫方程为

(12)

由式(2)～(10)可知

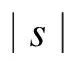
(13)

根据式(12)和(13)得到

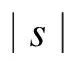
λarsh(s)]s

(14)

由式(14)可以看出,当选取式(11)的自适应律时,式(14)变为

λarsh(s)]s≤0

(15)

因此,可以看出式(11)所选择的自适应律是合理的.由控制律(10)可以看出，h1,h2参数的选取比较关键.如果h1,h2较小,趋近速度比较慢;反之h1,h2较大,趋近速度较大,参数可能会使系统产生抖振.对此,本文针对h1,h2两个参数采取自适应的方式进行估计处理.控制器设计为

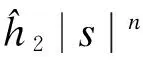
(16)

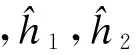
选取自适应律为

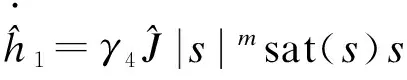
(17)

式中,γ4,γ5为选取自适应参量.

定理2若选取自适应律式(17),并采用式(16)的控制律,则被控系统能够保证在有限时间内收敛.

证明设计李雅普诺夫方程为

(18)

根据式(14)、(16)和(18)得

λarsh(s)]s

(19)

由式(19)可以看出,当选取式(17)的自适应律时,式(19)变为

λarsh(s)]s≤0

(20)

因此,根据Barbalat引理,容易得到当时间参数趋向无穷大时,系统的跟踪误差趋近于零,且最终系统处于稳定状态.以上从理论上证明了算法的有效性.

3 试验验证

选择链传动药仓台架作为试验对象.药仓控制系统方框图如图1所示,药仓控制系统包含上位机、控制器、驱动器、交流同步伺服电机、减速器、执行机构等.试验中参数选择:kp=0.5,ki=0.75,kd=0.1,λ=10,J初始值为3.36×10-4kg·m2,B初始值为2.016×10-3N·m·s/rad,γ1=γ2=0.000 1,γ3=γ4=0.001,γ5=0.05,m=1.1,n=0.5,Δ=1.25.

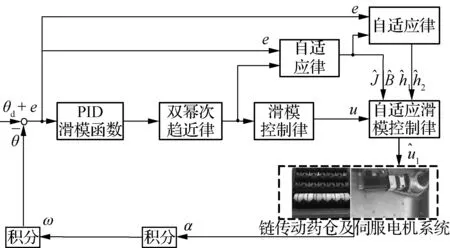
图1 药仓控制方框图

为了方便对比试验效果,设定期望运动角度θd、角速度ωd和角加速度αd轨迹,轨迹如图2所示.

试验过程中,分别进行了空载、半载和满载3种不同负载的试验.通过不同负载试验,进一步测试变负载情况下控制电流、跟踪误差及系统参数的变化情况.试验中获得的q轴输出控制电流曲线如图3所示,运行初期由于系统自身惯性导致控制电流较大,出现峰值;但随着系统的运行,在短时间内控制电流下降到较为平稳的状态.3种控制输出电流在运行后期均达到收敛稳定状态,稳定在较小的范围内.图4反映了在不同负载下运行跟踪误差状况.由图可以看出,不同负载下位置误差整体规律相近.在运行后期均稳定在较小范围内,跟踪误差满足e<2.5 rad,稳定误差满足e<0.8 rad的指标要求.图5为自适应参量在不同负载下的变化情况.各个参量在运行后期能够收敛到稳定的范围内,不同负载下参量变化较为明显.可以看出,在对变负载链传动药仓系统进行控制时,若将这些参量选择固定值，显然是不合理的.

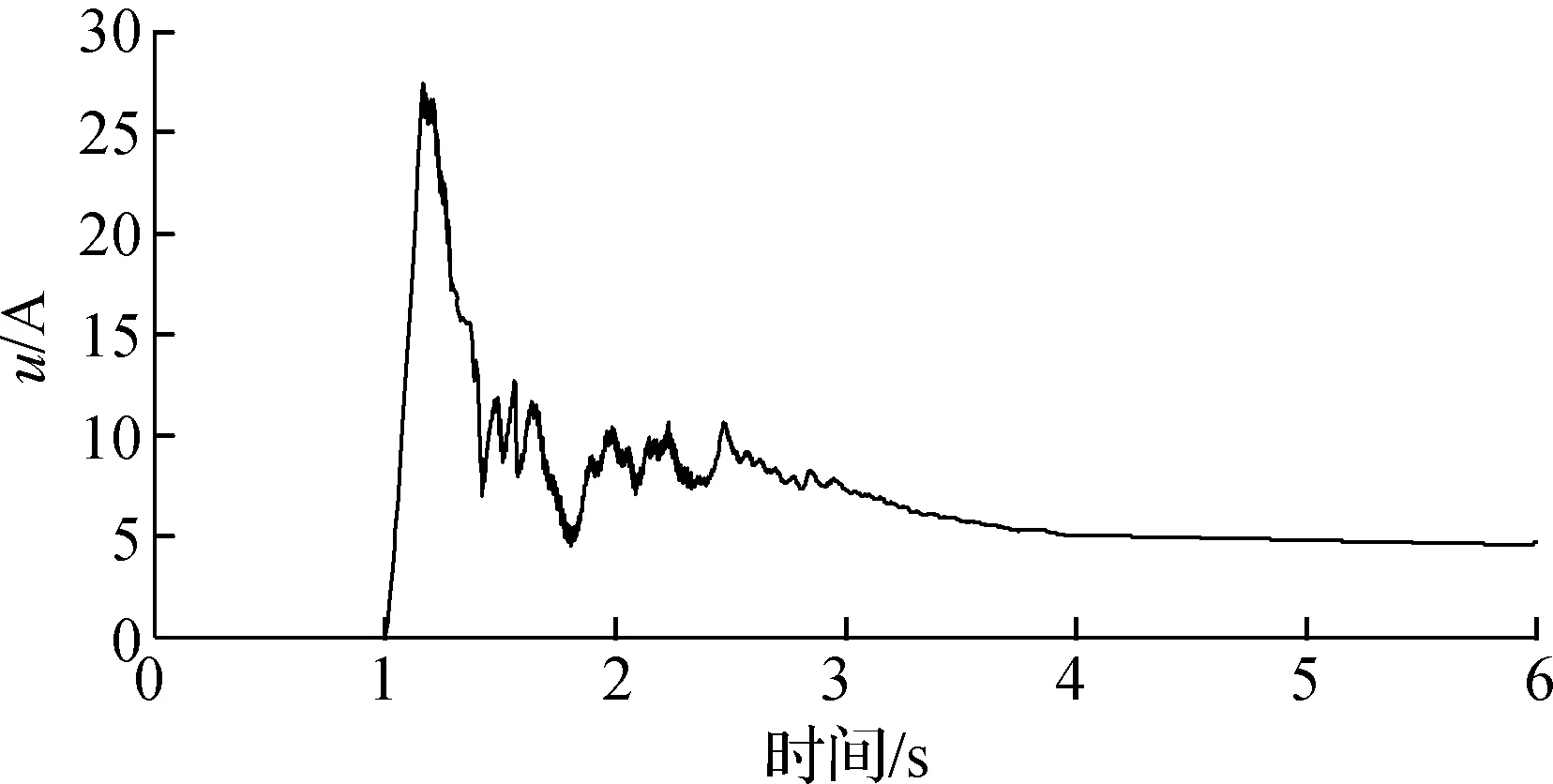
(a) 空载

(b) 半载

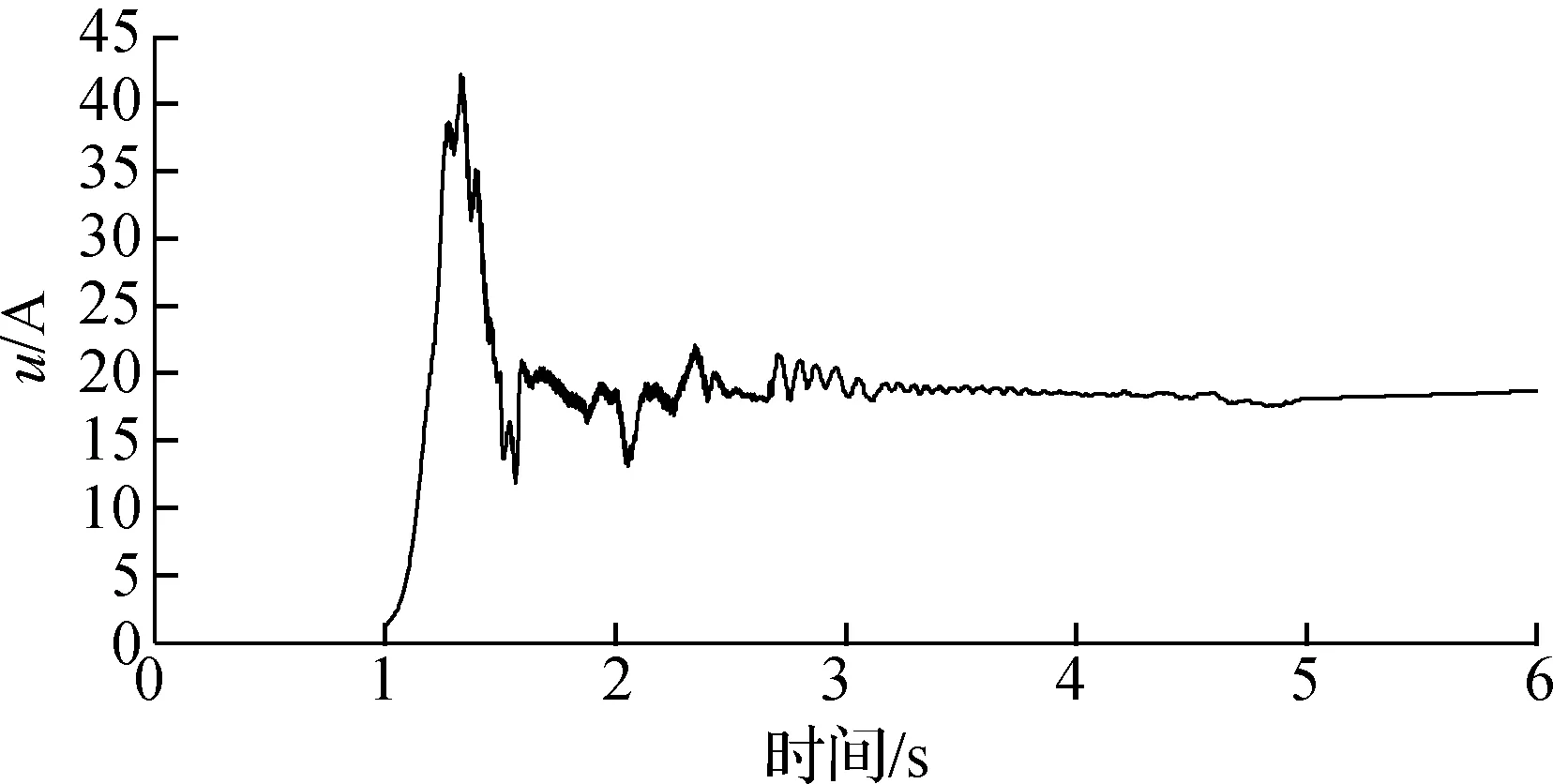
(c) 满载

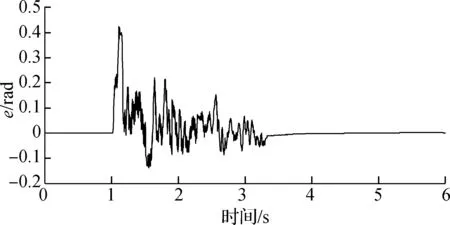
(a) 空载

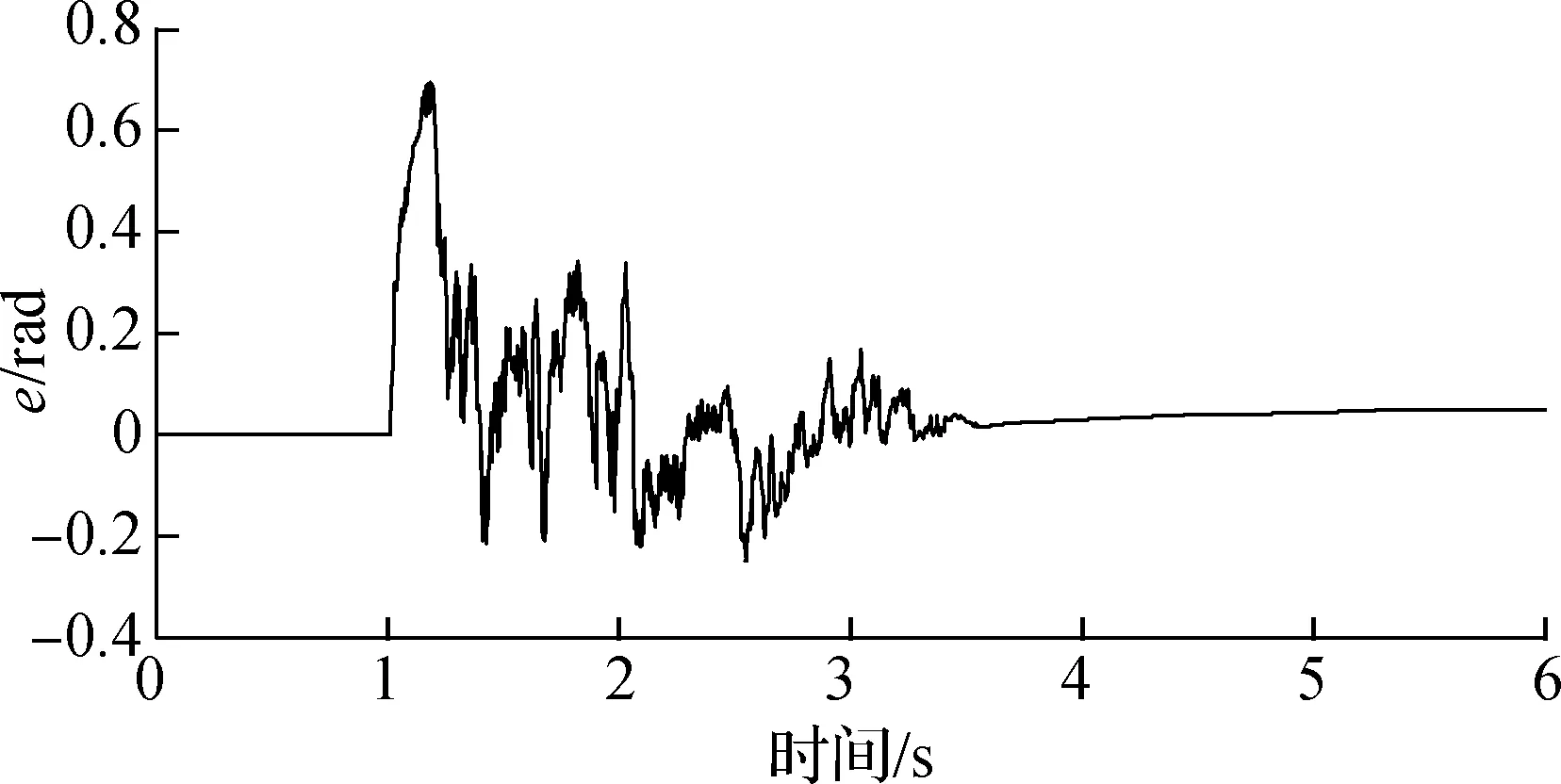
(b) 半载

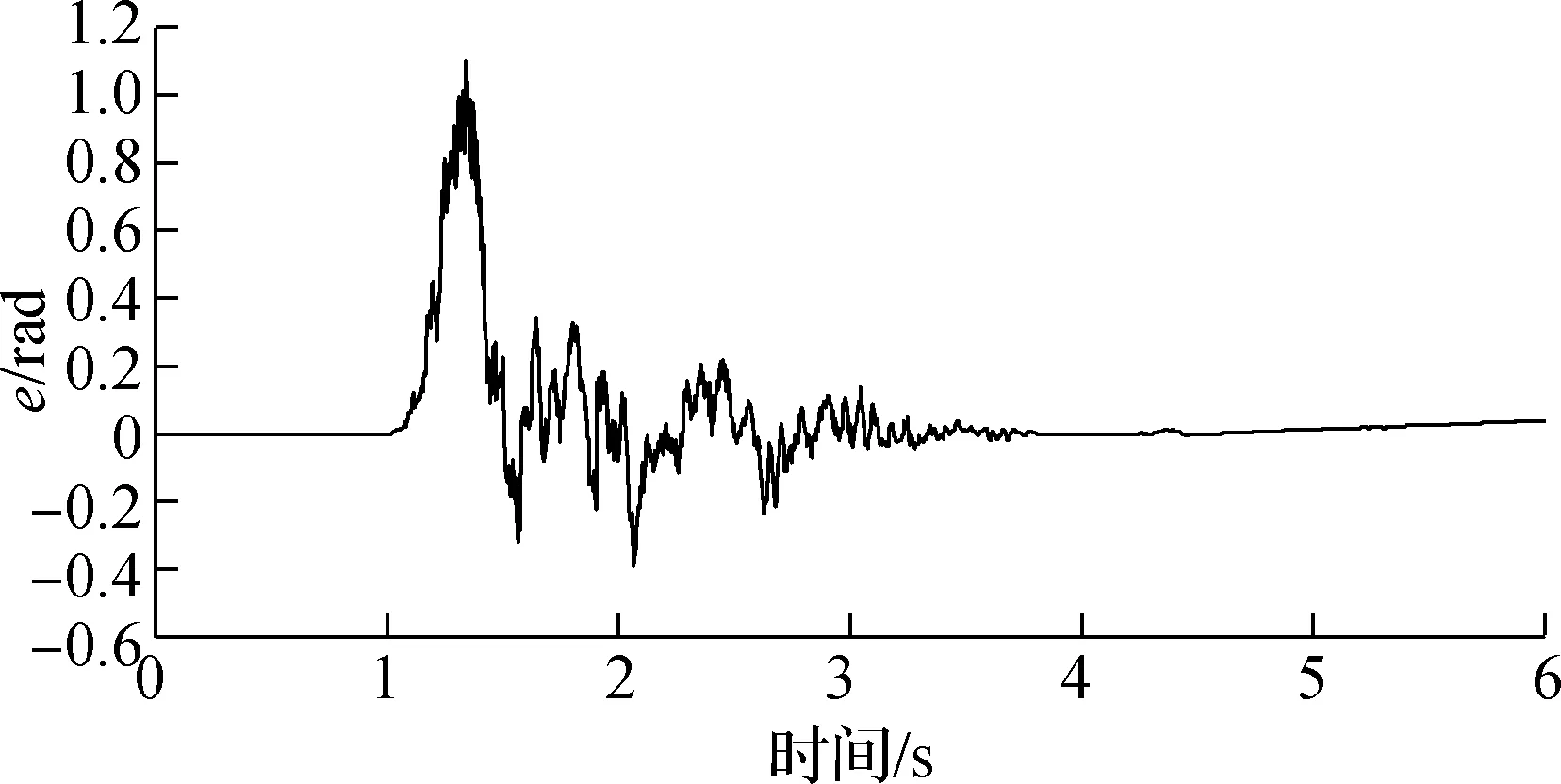
(c) 满载

4 结论

1) 本文对等效转动惯量和等效阻尼系数参数进行自适应跟踪控制,提高了控制器的准确性,进一步削弱了运动中的抖振.

2) 系统在该双幂次趋近律及自适应策略控制下具有较好的稳定性,提高了收敛速度,缩短了收敛时间.

3) 不同负载下系统的跟踪误差都比较小,具有较好的控制精度,满足指标要求.

4) 试验中测量噪声的存在对被控对象运动的平稳性产生一定的影响.后续将通过分析处理测量噪声来提高系统运动的平稳性.

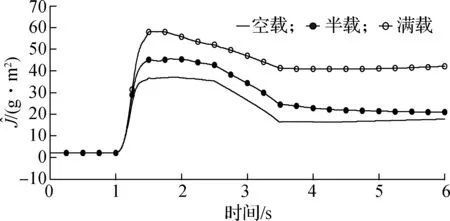
(a) 估计值

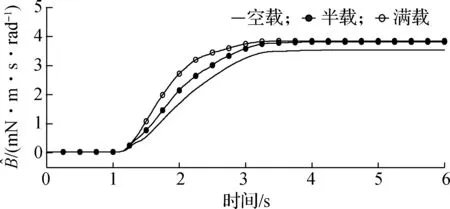
(b) 估计值

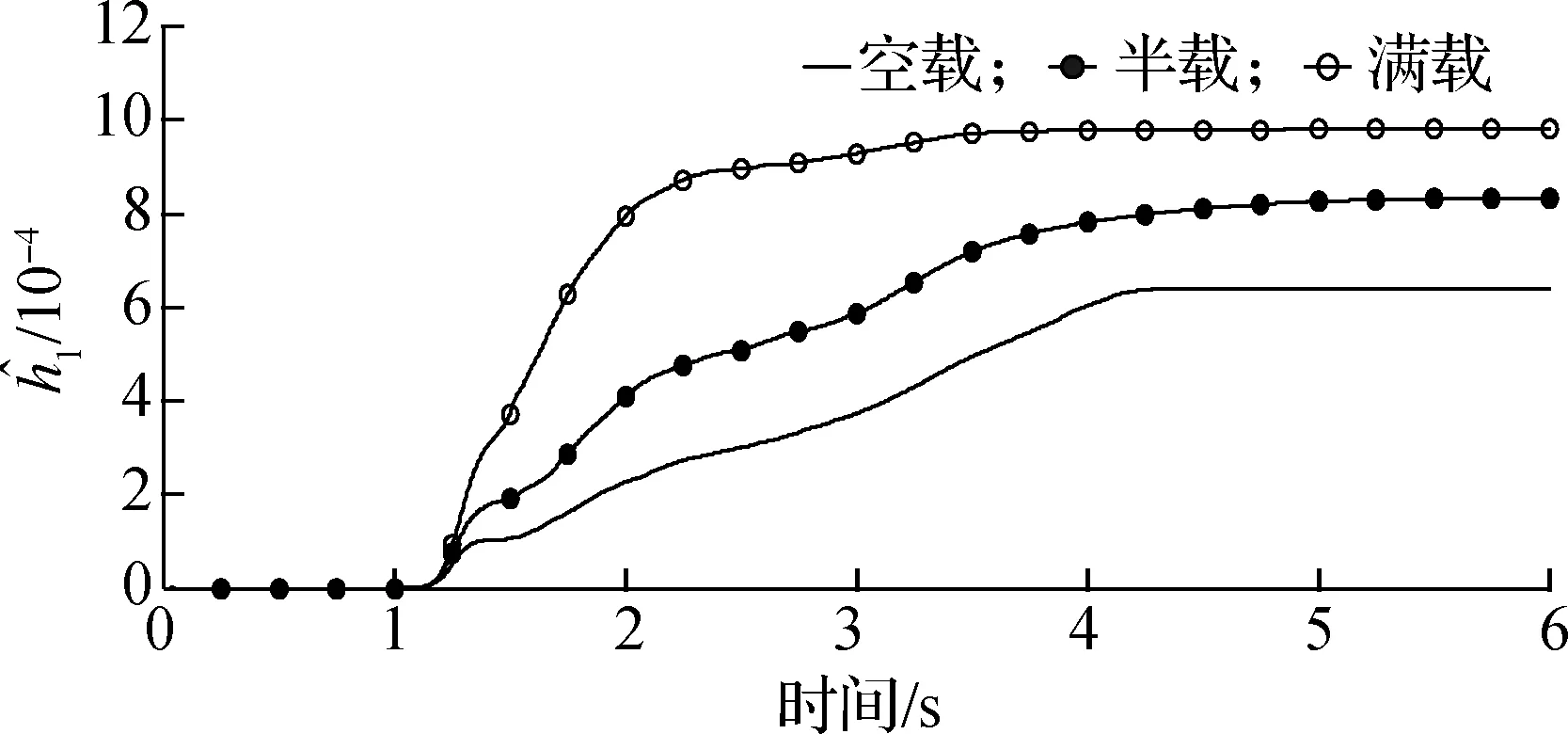
(c) 估计值

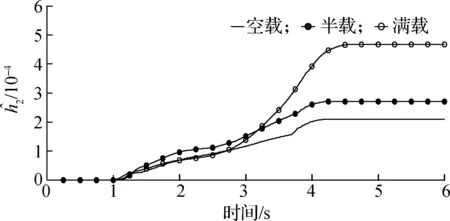
(d) 估计值

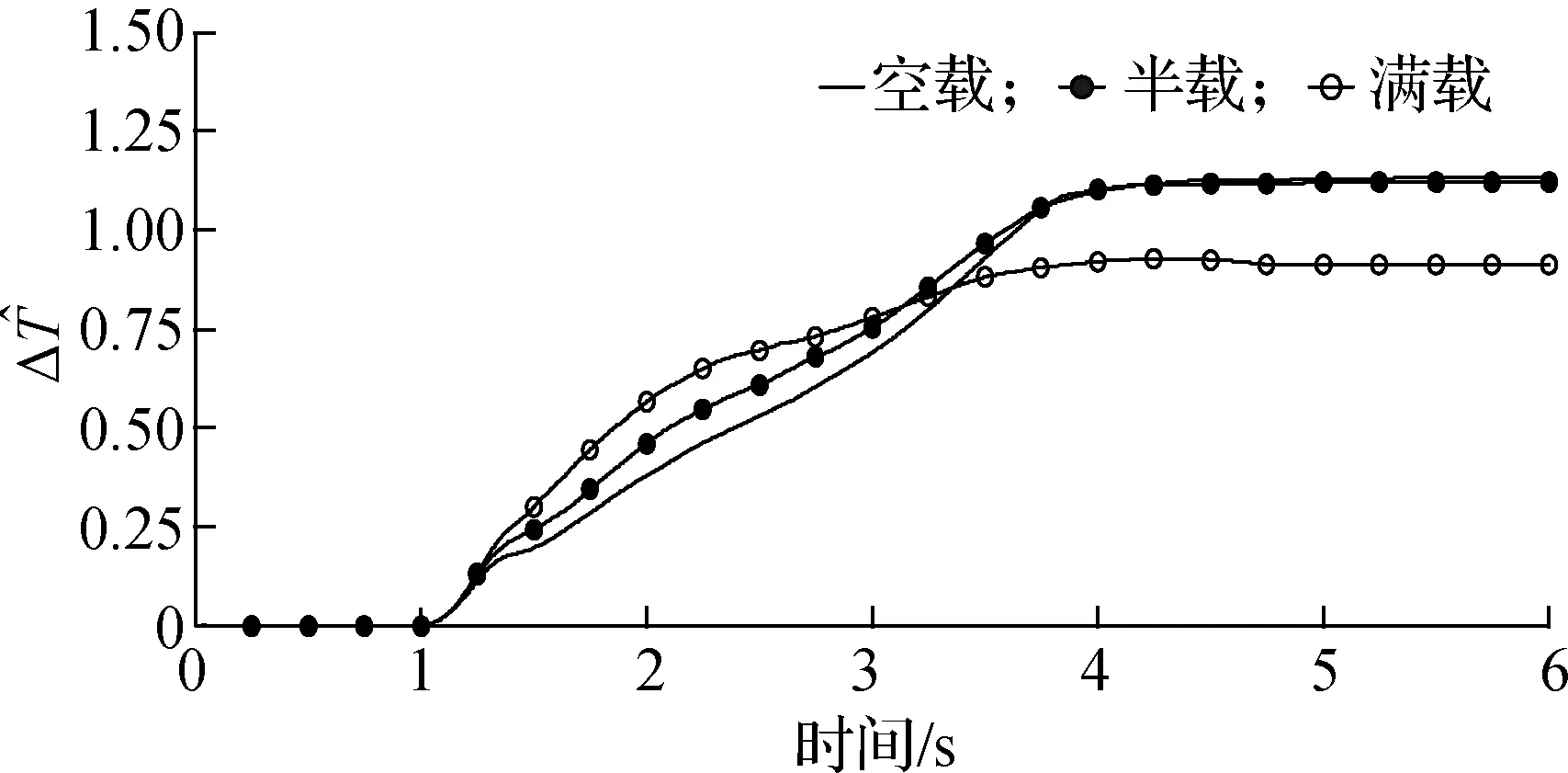
(e) 估计值

[1] 荣长发. 链传动的振动和噪声研究现状与发展[J]. 机械传动, 2004, 28(2):63-66. DOI:10.3969/j.issn.1004-2539.2004.02.023.

Rong Changfa. The present situation and development of vibration and noise based on chain driving systems[J].JournalofMechanicalTransmission, 2004,28(2):63-66. DOI:10.3969/j.issn.1004-2539.2004.02.023. (in Chinese)

[2] 邹权, 钱林方, 徐亚栋,等. 旋转弹仓的自适应模糊滑模控制[J]. 东南大学学报(自然科学版), 2015, 45(1):63-68. DOI:10.3969/j.issn.1001-0505.2015.01.012.

Zou Quan, Qian Linfang, Xu Yadong, et al. Adaptive fuzzy sliding mode control of rotational shell magazine[J].JournalofSoutheastUniversity(NaturalScienceEdition), 2015,45(1):63-68. DOI:10.3969/j.issn.1001-0505.2015.01.012. (in Chinese)

[3] 盖江涛, 黄守道, 周广明,等. 双电机耦合驱动履带车辆自适应滑模转向控制[J]. 兵工学报, 2015, 36(3):405-411. DOI:10.3969/j.issn.1000-1093.2015.03.004.

Gai Jiangtao, Huang Shoudao, Zhou Guangming, et al. Adaptive sliding mode steering control of double motor coupling drive transmission for tracked vehicle[J].ActaArmamentarii, 2015,36(3):405-411. DOI:10.3969/j.issn.1000-1093.2015.03.004. (in Chinese)

[4] 郭健, 吴益飞, 陈庆伟,等. 具有输入齿隙的一类非线性系统自适应控制[J]. 兵工学报, 2011, 32(10):1298-1304.

Guo Jian, Wu Yifei, Chen Qingwei, et al. Adaptive control of a nonlinear system with input backlash[J].ActaArmamentarii, 2011,32(10):1298-1304. (in Chinese)

[5] Liu Z, Su H, Pan S. A new adaptive sliding mode control of uncertain nonlinear systems[J].AsianJournalofControl, 2014,16(1):198-208. DOI:10.1002/asjc.657.

[6] Nasiri A, Kiong Nguang S, Swain A. Adaptive sliding mode control for a class of MIMO nonlinear systems with uncertainties[J].JournaloftheFranklinInstitute, 2014,351(4): 2048-2061. DOI:10.1016/j.jfranklin.2012.12.019.

[7] Shao S Y, Chen M, Yan X H. Adaptive sliding mode synchronization for a class of fractional-order chaotic systems with disturbance[J].NonlinearDynamics, 2016,83:1855-1866.

[8] 高为炳. 变结构控制的理论及设计方法[M]. 北京:科学出版社, 1996:211-225.

[9] 周涛. 基于一种新型趋近律的自适应滑模控制[J]. 控制与决策, 2016, 31(7):1335-1338. DOI:10.13195/j.kzyjc.2015.0518.

Zhou Tao. Adaptive sliding control based on a new reaching law[J].ControlandDecision, 2016,31(7):1335-1338. DOI:10.13195/j.kzyjc.2015.0518. (in Chinese)

[10] Lesniewski P, Bartoszewicz A. Inverse tangent based switching type reaching law for discrete time sliding mode control systems[C]//IEEEEuropeanControlConference. Linz, Austria, 2015:2390-2395.

[11] Chakrabarty S, Bandyopadhyay B. A generalized reaching law for discrete time sliding mode control[J].Automatica, 2015,52:83-86.

[12] Bartoszewicz A, Lesniewski P. New switching and nonswitching type reaching laws for SMC of discrete time systems[J].IEEETransactionsonControlSystemsTechnology, 2016,24(2):670-677.

[13] Chakrabarty S, Bandyopadhyay B. A generalized reaching law with different convergence rates[J].Automatica, 2016,63:34-37. DOI:10.1016/j.automatica.2015.10.018.

Adaptivecontrolforartillerychaindrivingpowderbasedondoublepowerreachinglaw

Yue Caicheng1Qian Linfang1Chen Longmiao1Tian Lingfei1Yang Huidong2

(1School of Mechanical Engineering, Nanjing University of Science and Technology, Nanjing 210094, China) (2North Automatic Control Technology Institute, Taiyuan 030006, China)

Aimed at some problems that when the artillery chain driving powder system moved, wide variations of load, indefinite parameters, chattering, and nonlinear friction existed. An adaptive sliding mode control scheme was proposed to solve these problems. The equivalent moment of inertia and the disturbance torque of the system were adaptively estimated. In this way, the impact of parameter uncertainty was mitigated and the system mathematical model was more accurately. The chattering problem of the system was restrained by using a new double power reaching law. Parameters of the reaching law were selected online by using adaptive methods. The robustness of the reaching and switching processes was enhanced. Experimental verifications of the system under different loads were conducted. The results show that the artillery chain driving powder system has better stability and position accuracy by using the control scheme under three conditions, i.e., empty-loaded, half-loaded and full-loaded ensuring that the output dynamic error of the motor is less than 2.5 rad and the steady state error is less than 0.8 rad.

artillery chain drive powder; chattering; adaptive control; double power reaching law

10.3969/j.issn.1001-0505.2017.06.009

TP273

A

1001-0505(2017)06-1135-06

2017-06-05.

岳才成(1990—),男,博士生;钱林方(联系人),男,博士,教授,博士生导师,lfqian@vip.163.com.

国家自然科学基金资助项目(11472137)、江苏省自然科学基金资助项目(BK20140773).

岳才成，钱林方，陈龙淼，等.基于双幂次趋近律火炮链传动药仓自适应控制[J].东南大学学报(自然科学版),2017,47(6):1135-1140.

10.3969/j.issn.1001-0505.2017.06.009.