一道女子奥林匹克竞赛试题的简证与推广

中国教育科学研究院丰台实验学校 李雅萍 (邮编：100071)

一道女子奥林匹克竞赛试题的简证与推广

中国教育科学研究院丰台实验学校 李雅萍 (邮编：100071)

对2011年女子数学奥林匹克竞赛不等式证明题给出了一个新颖简洁的证明;同时得出了这个竞赛不等式的一个加强;最后得到此类问题的n元推广.

女子奥林匹克;简证;推广

在2011年第10届女子数学奥林匹克竞赛中有一道优美的不等式试题：

(第10届CMO)已知a、b、c、d为正实数,且abcd＝1,求证：

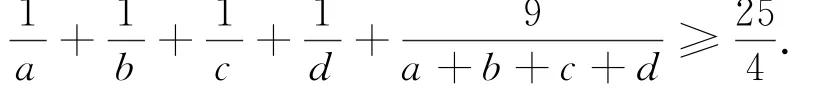
赛题结构简洁,形式对称优美,但证明的难度很大。竞赛命题组给出的参考答案([1])是利用讨论思想并结合调整法来处理的,技巧性较强且过程相当繁复,学生难以理解并掌握.为此,笔者对试题进行了深入的研究,得到了该竞赛试题的简洁证明如下：

试题另证 由对称性,不妨设a≥b≥c≥d＞0,因正实数a、b、c、d满足abcd＝1,故四个数中只有三个独立变量,将b、c视为常数,d＝,则不等式左边为a的函数

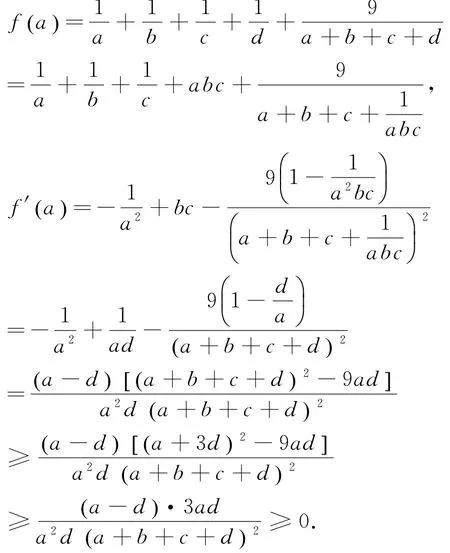
因此,函数f(a)在 [d ,＋∞)上单调递增,故当且仅当a＝d,此时a＝b＝c＝d＝1时

采用上述证明方法,立得赛题的一个加强：

另外,我们采用同样的方法,还可将这个命题推广为比文[2]更强的结论：

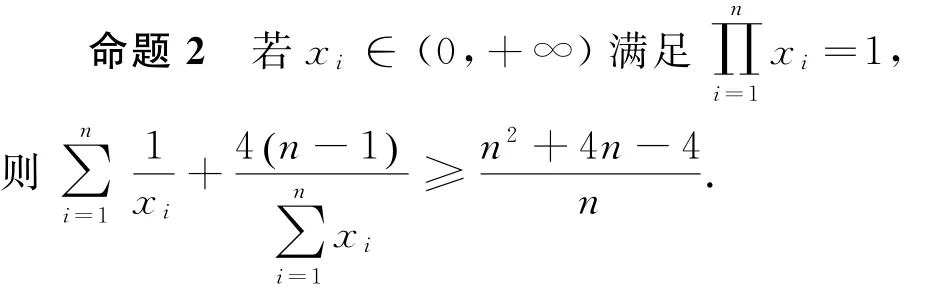
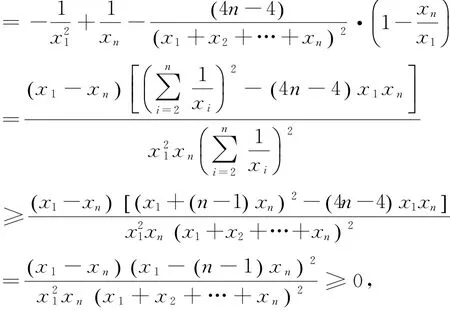
因此,函数f(x1)在 [xn,＋∞)上单调递增,故当且仅当x1＝xn,此时x1＝x2＝…＝xn＝1时,f(x)＝,所以原不等式1min成立.

1 2011女子数学奥林匹克[J].中等数学,2011(10)

2 查正开.数学奥林匹克问题高318[J].中等数学,2011(4)

2017-09-24)