2017年高考不等式试题的解法探究

江苏省常熟市中学 查正开 (邮编：215500)

2017年高考不等式试题的解法探究

江苏省常熟市中学 查正开 (邮编：215500)

根据题目中条件与结论的结构特征,通过添加合适或待定的零元,利用配方、均值不等式等手段完成问题解答的方法称为“加零”法[1].本文将用“加零”法来解答2017年高考数学的有关不等式试题,供读者教学与研究时参考.

将目标式加上零元并利用均值不等式,得

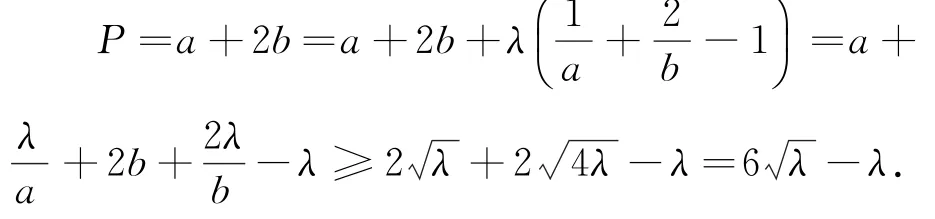
则得P≥9(当且仅当a＝b＝3时取等号).因此所求a＋2b的最小值为9.

值得指出的是若改变条件式或目标式,则常数代换法或柯西不等式等方法就难以奏效.譬如题目的其他条件不变,改求a＋b2的最小值.则常数代换法将无功而返,采用柯西不等式也很难获得求解,而采用“加零”法可一样轻松搞定.解答如下：

例2 (2017年高考江苏卷理科加试第21题)已知a、b、c、d为实数,且a2＋b2＝4,c2＋d2＝16,证明：ac＋bd≤8.

证 明 构 造 零 元 －λ(a2＋b2－4)－μc(2＋d2－16),则

P＝ac＋bd＝ac＋bd－λ(a2＋b2－4)－μc(2＋d2－16)＝ (ac－λa2－μc2)＋(bdλb2－μd2)＋4λ＋16μ＝－ (a)2－2＋4λ＋16μ≤4λ＋16μ.

当且仅当aλ＝cμ,bλ＝dμ,2λμ＝1时,不等式取等号,代入已知条件,得λ＝1,μ＝⇒P≤8,所以不等式ac＋bd≤8成立.

例3 (2017年高考全国卷I(II、III)理科第23题)已知a＞0,b＞0,a3＋b3＝2,证明：(1)(a ＋b)(a5＋b5)≥4;(2)a＋b≤2.

证明 (1)根据不等式左边代数式的特征,结合已知条件构造零元－[(a3＋b3)2－4]则(a＋b)(a5＋b5)＝(a＋b)(a5＋b5)－[(a3＋b3)2－4]＝(a6＋b6＋ab5＋a5b)－(a6＋b6＋2a3b3－4)＝ab5＋a5b－2a3b3＋4＝ab(a2－b2)2＋4≥4;

(2)运用已知条件要证明的不等式等价于a＋b( )3≤8⇔a3＋b3＋3a2b＋3ab2≤8⇔a2b＋ab2≤2.

因此可构造零元－(a3＋b3－2),则

a2b＋ab2＝a2b＋ab2－(a3＋b3－2)＝a2(b－a)＋b2(a－b)＋2＝(b－a)(a2－b2)＋2＝－(a－b)2(a＋b)＋2≤2,

即不等式a2b＋ab2≤2成立,所以原不等式a＋b≤2成立.

评析 “加零”法一般都是利用条件,通过将目标代数式加上一个含有参数的零元,利用配方或均值不等式等手段通过研究等号成立条件确定参数的值再作出解答的.但在具体解题操作时可根据题目的结构特征尝试添加合适的零元直接完成求解.

例4 (2017年高考天津卷理科第12题(文科12))若a、b∈R,ab＞0,求最小值.

评析 本题是一个高考试题命题组精心命制的最值问题,因它是一个非齐次的代数式,学生处理起来比较困难.下面,再给出此题的另外两种解法：

方法1 由条件ab＞0利用四元均值不等式,得

1 查正开.“加零”法的应用[J].数学教学,2015(7)

2017-09-19)