彰显数学文化的弧度制教学设计

安徽师范大学数学计算机科学学院 刘芹芹 陈克胜 (邮编：241000)

彰显数学文化的弧度制教学设计

安徽师范大学数学计算机科学学院 刘芹芹 陈克胜 (邮编：241000)

《普通高中数学课程标准(实验稿)》的基本理念之一是体现数学的文化价值,但在数学课堂真正体现数学文化仍值得我们进一步去研究.数学文化的物质基础是知识体系、应用框架是工具性、得以发扬的源泉是隐形价值、历史积淀是数学史,以高中数学课程“弧度制”的教学为研究对象,从这四个层面改造弧度制教学设计,彰显弧度制的数学文化,真正将数学文化融入课堂,在此基础上,提出在数学课堂中彰显数学文化的一点思考.

弧度制;数学文化;弧长;教学设计

1 “弧度制”的数学文化内涵

弧度制的数学文化内涵可以这样思考：以弧度制的概念作为数学文化教育的载体,在教育载体的背后隐藏着数学文化的价值内涵,换言之,用“长度”度量角是人类思想的巨大转变,是用“度”度量角思想之后的又一个解决角度问题的关键性思想;弧度制本质上是通过常用度量衡中长度的比例计算思想,统一了角和长度的单位,彰显了数学的对称美;弧度和弧度符号的数学史展示了数学文化丰富的历史积淀,体现了数学的符号化思想,体现了数学的简洁美;弧度制的数学文化决定了人的思维方式转变,在解决实际问题时提供有鲜明特色的思考方式,实际问题往往大多源于生产实践,因而,数学文化在很多方面为社会直接创造价值.

2 “弧度制”的教学设计

(一)特殊引入——易于转换思维

在单位圆中,半径绕着它的端点旋转一周所形成的角度都是“360°”,是不变的定值,用角作为单位来度量角的单位制叫做角度制,角度制规定圆周的360分之一为1度的角.同样,在单位圆中,,“C＝2π”也是不变的定值,我们可以分割圆周长找度量单位,将半径作为度量单位度量弧长,由此得到＝1”时,此时弧长所对的角叫1弧度的角,用符号rad表示,读作弧度,这样就可以用弧长来刻画角度,实现了弧长与角度在量上的对等,这种以弧度为单位度量角的单位制就称为弧度制.

“弧度(radian)”一词,是爱尔兰工程师詹姆斯·汤姆森(JamesThomson)在1875年首先创造使用的,由半径(radius)和角(angle)两个英语单词组合而成.1935年,我国《数学名词》把radian译为“弪(弧和径两字合成,读jing)”,这表明圆心角的弧度数是由弧长和半径r共同决定的.1956年版的《数学名词》废除此字,定为弧度(梁宗巨,2000)[1].

弧度的符号表示在历史上也几次变换.1881年霍尔斯特德(Halsted)用ρ表示弧度单位;1909年霍尔(Hall)等用R表示;1907年鲍尔(Bauer)用r表示.直到1925年朗尼(Loney)的《平面三角》还用πc表示.近几十年来,数学家却习惯将弧度的符号省去不写[1].这里老师提醒学生不写“弧度”二字或弧度符号不等于没有,依旧是一个量而非实数,要注意和实数的区别.

思考 上述弧度制是在单位圆中给出定义的,那在非单位圆的圆中是否依然成立呢?

设计意图 从单位圆出发,将定值“2π”与学生原有认知结构中的定值“360°”建立起实质性联系的过程,更容易使学生转化思维方式.从数学文化的角度出发,在学生已有认知结构知识的基础上,将学生的思维方式从角作为单位来度量角转换为从弧长作为单位来度量角,使学生对弧度制有初步的感性认识.问题的引入激发了学生探究新知的欲望,提高了学生的好奇心,为本节课作下了良好的铺垫.

彰显的数学文化 其一,建构主义认为学习是学习者基于原有的知识经验生成意义、建构理解的过程,以学生的知识系统作为数学文化的物质基础,借助定值“360°”研究定值“2π”,建构一种学生思考问题的方法,在学生潜移默化的转变思维方式的过程中发挥着其文化价值的作用.其二,体现用弧长度量角的思想.其三,从数学史的角度,将弧度和弧度符号的由来置于丰富的数学文化内涵之中,体现了数学符号的简洁美,陶冶了学生的审美情操,对于提高学生的文化修养起着重要的作用.

(二)特殊到一般——得出弧度制概念

在非单位圆的圆中,由于r≠1,弧长与角度在量上虽然是不对等的,但只需要将等于半径长的弧所对的角定义为1弧度的角,即1弧度的角所对弧长等于半径,用符号rad表示,读作弧度,依然可以利用“弧长”来刻画其他的角,比如2弧度的角是此“弧长”的2倍,3弧度的角是此“弧长”的3倍等等.这节课之前我们将角的概推广到任意角,有正角、负角、零角,但弧长与半径的比值不可能为负.一般地,正角的弧度数是一个正数,负角的弧度数是一个负数,零角的弧度数是0,如果半径r的圆的圆心角α所对弧的长为l,那么,角α的弧度数的绝对值是,这里,角α的正负由角α的终边旋转方向决定[3].

思考 弧度制作为角的另一种度量单位,如何与角度制转换的呢?

设计意图 从单位圆到非单位圆的圆,从特殊到一般,利用学生思维已有弧长度量角的思想自然而然得出弧度制的概念.从数学文化出发,在数学教学中介绍“弧度制”的发展历程,让学生知道它们不是凭空出现,是前人积极探索的结果.

彰显的数学文化 其一,常用度量衡中长度的比例计算思想,特殊到一般的思想,用“长度”度量角的思想,向学生揭示了一种科学的思维方法,优化了学生的思维,体现了数学文化对学生的精神影响.其二,借助数学史上角的其它度量方式并不能使进位制统一的问题,将弧度制的由来置于丰富的数学文化内涵之中,进一步表明引入弧度制不是为了引入而引入,而是解决了进位制统一的问题,让学生真正感受到现实世界需要这种数学文化内涵以及引入弧度制的可行性.其三,数学史上的数学家所遇到的困难,同样也是学生在学习过程中遇到的困难,向学生介绍数学家解决问题的研究历程,反映出人类对数学研究的精神,让学生感知数学家探求知识的艰难,培养学生的探索科学的精神.这种以弧度制的史实系统作为载体,在学生逐步建立人文主义精神和数学观念的同时,发挥着重要的数学文化价值.

36例患者影像测量结果见表3。术后侧凸Cobb角较术前明显降低，差异具有统计学意义（P＜0.05）；前凸角度、椎间孔高度、椎间隙高度、椎间孔面积、椎管面积较术前明显升高，差异具有统计学意义（P＜0.05）。典型病例影像资料见图2。

(三)引导探究——理解角度与弧度的关系

圆转一周在角度制下度数是360,在弧度制下弧度数是2π,所以

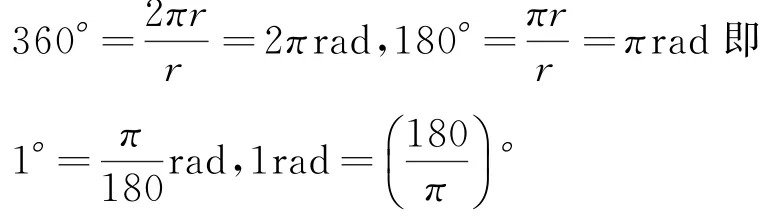
其他[0,2π]内的特殊角,可以通过类比如图1和图2所示的“形”化出来.

这样,在弧度制条件下,角的集合与实数集R之间就可以建立一一对应的关系,这也为后面学习把三角函数看成以实数为自变量的函数打下了基础.

设计意图 使学生领悟到角度制、弧度制都是角的度量制,二者虽然单位不同,但是是互相联系,相互统一的,更容易看清角与实数的一一对应关系,从而解决了“sin30°＝”这类进制不统一的问题.

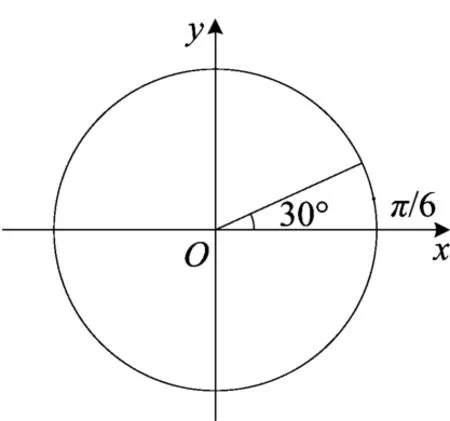
图1 特殊角的图形

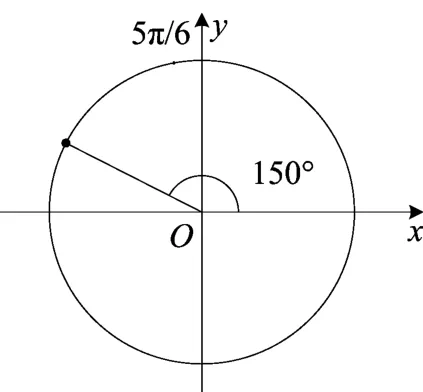
图2 特殊角的图形

彰显的数学文化 其一,用直观的图形将弧度制与角度制关系联系起来,让学生学会将复杂繁多的问题直观化,感受图形所带来的方便简洁美,从而让学生体会到数学所带来的快乐,欣赏弧度制之美.其二,在直角三角形中,弧度作为三角函数的自变量等于圆弧长与半径的比值,而三角函数的自变量是三角形边长的比,从而可以得出三角函数是从长度的比值到长度的比值的映射,使自变量与因变量的形式统一,极大的彰显了数学的统一美.

(四)及时应用——体会弧度制精髓所在

①75° ②22°30′ ③－265°

例2 按照下列要求,将弧度化为角度.

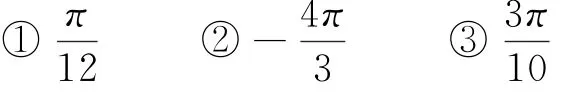
例3 利用弧度制证明下列关于扇形的公式[3];

其中R是半径,l是弧长,α(0＜α＜2π)为圆心角,S是扇形的面积.

设计意图 例1和例2是让学生掌握弧度制和角度制的转换过程,加深对弧度制的理解和应用.通过例3使学生自然而然的体会到弧度制可以简化公式,如为求扇形的面积和弧长提供了方便,从而大大简化了有关公式及其运算并培养学生应用数学的能力和意识.

彰显的数学文化 其一,在解决问题的过程中,让学生体会利用弧度制刻画面积公式,感受弧度制给我们学习生活所带来的简便,潜移默化中改变学生的思维方式,体现数学文化的隐形价值.其二,人渴望欣赏美,数学之美正是人所需要的,弧度制下的圆的面积和弧长公式的流畅,推理的精炼,等式两边度量衡的统一,彰显了数学的统一美,弧度制下的圆的面积和弧长公式与角度制下的圆的面积和弧长公式对比,极大的彰显了弧度制的简洁美.

(五)小结作业——理顺熟练知识

(1)小结

不管圆的大小如何发生改变,圆的周长与直径的比值都是“π”,无理数“π”具有浓密的传奇韵味,在以后学习中让我门慢慢用心去品味他.

弧度制成为角的度量单位之一,可以与角度制进行换算,即

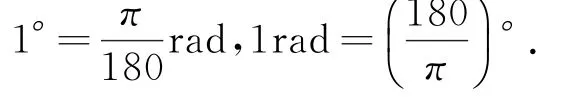
用弧度制度量角,不仅数量简单,而且由此更容易看清角与实数建立一一对应关系.

本节课有鲜明特色的思想是用“长度”刻画角,我们要学会用这种思想去处理各种问题.

(2)作业

必做题：课后练习.选做题：发挥你的创造性,每人制作一把扇子,然后与其他同学进行比较,从中选择出一把展开看上去形状较为美观的扇子,并用计算器算出它的面积[4].

设计意图：学生在教学回顾中,整理知识,建立对弧度制的整体意识,整体地了解把握弧度制.选择与学生实际生活相关的课后习题,使学生体会弧度制的好处,培养学生将实际问题数学化,学以致用并认识任何新知识的都会为我们解决实际问题带来方便,从而激发学生的学习兴趣.

彰显的数学文化：将弧度制与学生的实际生活紧密联系起来,让学生将实际问题数学化,真正感受到数学文化在数学中内涵,数学是为人类自身服务,人类文明发展至今,可以说生活离不开数学,数学使生活更精彩[4].

3 一点思考

2016年10月8号,教育部考试中心公布了[2016]第179号文件《关于2017年普通高考考试大纲修订内容的通知》,关于数学学科具体修订内容有如下描述“在能力要求内涵方面,增加了基础性、综合性、应用性、创新性的要求,增加了数学文化的要求.同时对能力要求进行了加细说明,使能力要求更加明确具体”其中对数学增加了数学文化的要求.这一文化从考试大纲的角度明确要求在数学试题中融入数学文化,今后的高考试题中也定会有所体现.数学文化在教学如何成功的彰显出来,对广大数学教育者而言,是一个重要的课题.数学文化是一个笼统的概念,正因为每个数学教育者对数学文化的理解不一样,导致教学设计的思路不一样.高中数学教学中可以通过介绍数学史、数学的美、数学思想方法、课本习题后面的阅读与思考、数学的应用渗透数学文化,彰显数学文化对人类的精神影响、对社会创造的直接价值、对人行为的影响以及对人类审美情操的陶冶.

1 王越偲.上海高中生对弧度制概念的理解[D].上海：华东师范大学,2010

2 江灼豪,何小亚.弧度制发展的历史溯源[J].数学通报 .2016(7)：14-17

3 中学数学课程研究开发中心.普通高中课程标准实验教科书数学必修4[M].北京：人民教育出版社,2007

4 陈克胜,董杰.彰显数学文化的一元一次方程的教学案例及其思考[J].内蒙古师范大学学报(教育科学版)2012(2)：135-138

2017-09-28)