适用于RFID的轻量级算法的实现和评估∗

于钧合 侯文瑞 徐铭泽

（1.海军陆战学院 广州 510430）（2.海军参谋部 北京 100841）（3.海军工程大学理学院 武汉 430033）

适用于RFID的轻量级算法的实现和评估∗

于钧合1侯文瑞2徐铭泽3

（1.海军陆战学院 广州 510430）（2.海军参谋部 北京 100841）（3.海军工程大学理学院 武汉 430033）

随着RFID技术的快速发展，其安全问题也越来越严峻，论文结合RFID系统的特点，对在其中应用较为广泛的HIGHT、KLEIN、TEA和KATAN算法进行了分析和比较研究。首先，对这些算法的汇编代码进行了分析，确定相关操作和指令集的耗时情况。随后，在AVR单片机上执行这些算法，从能量消耗、扩散和混乱程度等方面对算法的安全性进行了比较研究。最后，将所有结果进行对比，指出代码分析结果和算法实际实现结果之间的不同。论文的研究成果既揭示了各算法之间的不同的性能又表明算法的实现结果和代码分析结果存在较大的差异。

RFID；轻量级算法；仿真

1 引言

RFID（Radio Frequency Identificatio）技术作为目前最热门的技术之一，在我们的生活中得到了广泛的应用［1］。RFID系统最大的优点就是实现成本比其它技术低很多，但该系统的隐私和安全问题也一直困扰着相关领域的研究人员，其中最主要的原因就是RFID这样的设备没有足够的硬件资源用来完成复杂的计算。

RFID是一种在不进行直接接触就能对物体进行识别的技术，它主要由三个部分组成：标签、读写器和后端处理系统。读写器是RFID的重要组成部分，它的功能是为标签提供向外发送信息的能量，同时对标签的信息进行收集并传送至后端系统处理［2］。

RFID系统很容易受到各种各样的攻击，包括主动攻击和被动攻击［3］。在RFID系统中有两种防御机制：基于主机的防御机制和集中防御机制。由于在无线网络中进行识别，RFID系统的标签和读写器始终处于不安全的环境之中，并且随着系统安全性的加强也会出现不同的威胁对其进行破解。随着大量的轻量级算法被分布出来，RFID系统的安全性有了进一步的提升。在电子标签中用不同的加密算法对信息进行加密会降低用户隐私被窃取的风险，但是又由于标签自身的限制，并不是的所有的算法都适用于任何一种标签，本文选取几个常用的轻量级算法从代码和实现结果等不同角度进行比较，并对比较结果进行归纳总结。

2 相关算法简介

2.1 KLEIN算法

KLEIN算法在2011年被提出，使用的是SPN（Substitution-permutation Network）结构。KLEIN算法的密钥长度有64、80和96位，算法根据密钥长度的不同有12、16和20轮迭代，在进行加解密时，主要采用面向字节的处理方式，在非线性结构中，使用了4bit并具有自反特性的S盒［4］。在扩散过程中，KLEIN算法的设计者将AES算法中的MixColumns函数通过改进变形成为MixNibbles函数，并与RotateNibbles函数相结合，使得函数在软硬件实现中效率都有所提升。算法通过密钥扩展过程得到一系列的轮密钥，这个过程采用了Feistel结构，主要有移位、异或等运算，图1展示了KLEIN-64算法的一次密钥扩展过程。

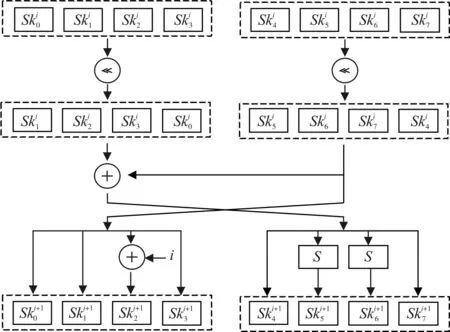
图1 一次密钥扩展过程

2.2 KATAN算法

KATAN算法有三种类型：KATAN32，KATAN48和KATAN64，所有的类型都使用80bit的密钥［5］。本文选取KATAN-48进行研究。KATAN32的明密文的分组长度最短，只有32bits，该算法的结构与流密码相似，如图2所示。算法共有254轮，每轮使用的非线性变换定义如下：

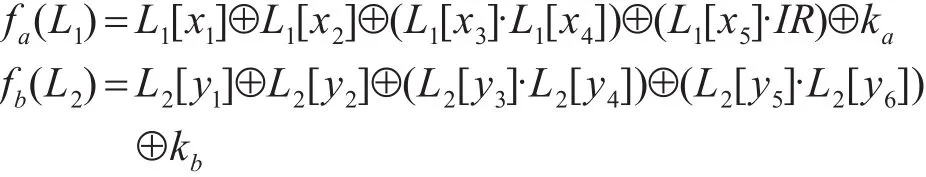
其中，IR是一个254位的数组，ka、kb都是子密钥。

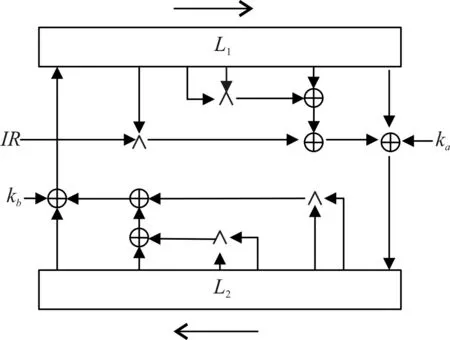
图2 KATAN算法结构

2.3 HIGHT算法

HIGHT算法的分组长度为64bit，使用的密钥为128bit，经过32轮计算。算法的主密钥有16个字节：MK=(MK15，MK14，…，MK0)，算法的加密过程如图3所示，WK和SK分别是白化密钥和子密钥 ，明 文 用 P=(P7，P6，…，P0) 表 示 ，密 文 用C=(C7，C6，…，C0)表示［6］。

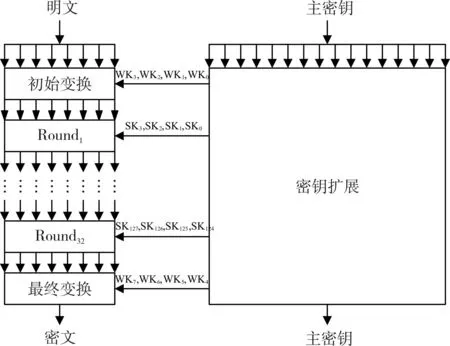
图3 HIGHT算法加密流程

2.4 TEA算法

TEA算法采用了Feistel结构，包含的主要运算方式是模加，异或和移位［7］。该算法的分组长度为 64bit，密钥长度为 128bit，运用了香农的扩散和混淆原则，提高了P盒和S盒的安全性。算法的结构如图4所示，算法通过交叉使用模加和异或来保证非线性。

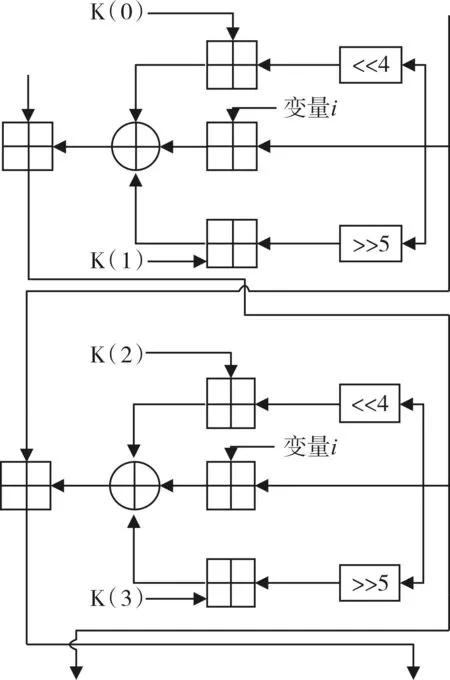
图4 TEA算法结构

3 算法的代码分析及比较

3.1 算法的时钟周期数

算法的时钟周期数根据算法代码中各组件需要执行的指令类型及次数计算出来，分析结果如图5所示。

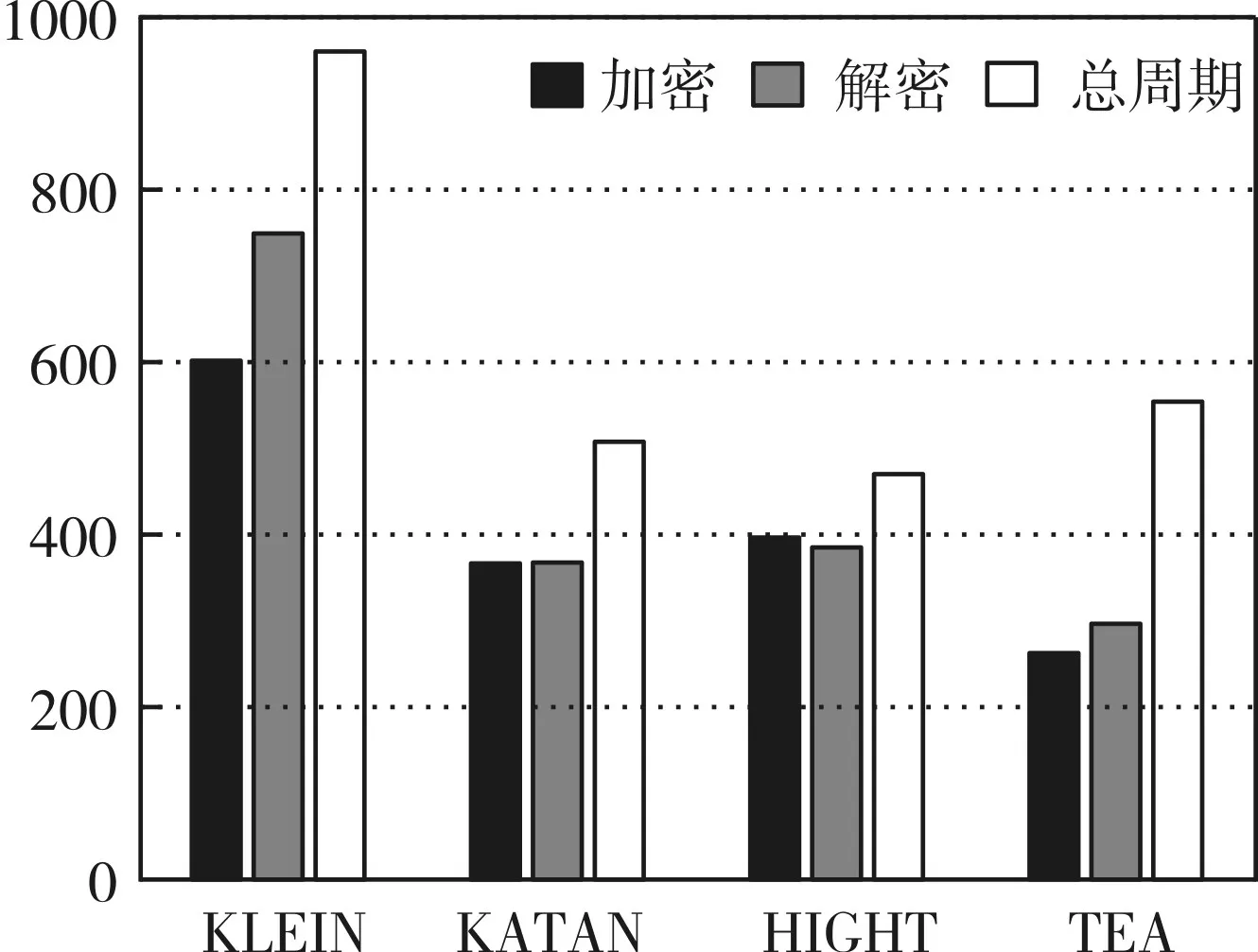
图5 算法的时钟周期数

图5 展示了各算法加密和解密的时钟周期数，总的周期数通过加解密周期数相加再减去重复的部分得到。由图中可以看出，HIGHT算法所用的周期数最少，表明此算法各组件的指令较少或每个指令使用的平均周期数最少，同时，与其它几个算法相比只有HIGHT算法的加密的时钟周期比解密的多，虽然实际运行的结果与代码分析有差异，但通过这样的分析有助于写出更高效的代码。KLEIN算法占用的时钟周期最多，因为与其它3个算法相比，KLEIN是唯一一个使用SPN结构的算法，在轮函数中的 MixColumns、RotateNibbles和SubNibbles步骤都需要较多的指令来完成运算。

对算法各组件指令周期的分析有助于对算法的实现性能进行改进，所以很有必要在算法实现前对各指令的耗时情况进行比较分析，从而根据实现平台的不同特性选取具有更高效率的运行方式，提高算法效率。

3.2 代码行数的比较分析

另外一种分析代码的方式是比较代码的长度来确定算法的复杂程度。对代码行数进行分析的结果也可以从一定程度上反应出算法的性能，从而更加有效地指导编写者对代码做出改进，提升算法性能。图6展示了各算法代码行数的分析比较结果。

从图中可以看出，KLEIN算法的代码行数最多，说明该算法比其它算法有更多的执行步骤。HIGHT算法的代码行数最少，这也是在代码分析中HIGHT占用时钟周期最少的原因。

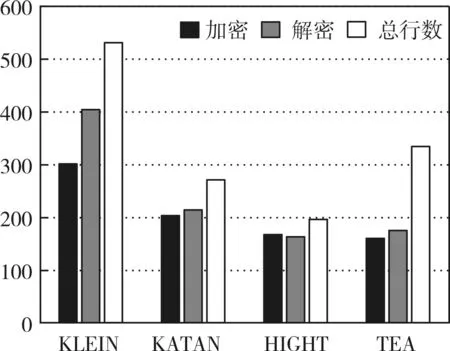
图6 各算法代码行数

造成KLEIN算法的代码长度最长的原因主要有两个。首先KLEIN使用的是SPN网络结构，SPN结构的加密和解密过程与Feistel结构不同，这种结构运行起来的代码行数普遍较多。另一个原因是KLEIN算法的主要步骤中包含AddRoundKey，RotateNibbles，MixNibbles和 SbuNibbles，每个函数都需要单独的代码，因此增加了代码的行数。HIGHT算法代码行数最少的原因是算法的结构，Feistel结构减少了代码的行数，另外，HIGHT算法的数学运算过程也进行了简化，执行过程中的加减、异或、移位等步骤比其它较复杂的函数运行起来更简单，也大大减少了代码长度。

4 算法硬件平台实现的性能对比评估

在对算法的实现性能进行对比研究中，本文的源代码以Thomas Eisenbarth［8］等人所做的相关研究为基础，对各算法在AVR单片机上进行实现，并整理了相关参数进行后续的对比分析，主要的对比项目有内存占用，时钟效率和能量消耗。

4.1 内存占用分析

图7展示了各算法实现后内存占用的百分比。

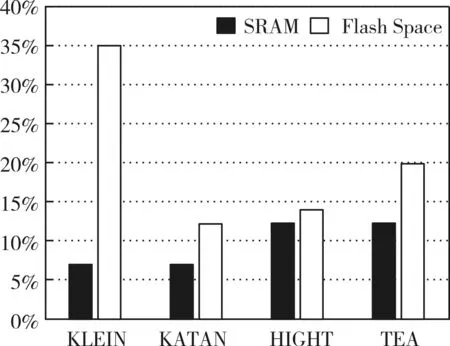
图7 各算法内存占用百分比

图中百分比的计算以单片机上SRAM和可编程Flash空间的大小为基础。从图中反映出的数据可以看出KATAN算法的SRAM和Flash的内存占用都比其它算法少，KLEIN算法占用了最多的Flash空间，因为由上节的分析可得该算法的代码长度最长，但SRAM的占用百分比与其它算法比起来就相对较少。

基于以上数据对比，KATAN算法更适用于对内存占用要求限制较高的设备，HIGHT和TEA算法的SRAM占用百分比相同，主要原因是这两个算法的密钥长度（128bit）和分组长度（64bit）都相同，同理KLEIN和KATAN算法的SRAM占用量也相同，两种算法的密钥长度和分组长度分别是80bit和64bit，又由于HIGHT和TEA的密钥长度比KLEIN和KATAN的密钥长度长，所以SRAM的占用量更高。Flash空间的占用量取决于汇编代码的大小，KLEIN算法代码的长度决定了占用的Flash空间最多，KATAN算法占用最少的Flash空间也是由于代码的长度最短。

4.2 CPU时钟周期消耗分析

通过在AVR单片上各个算法来获取参数，对加密和密钥扩展过程的耗费的时钟周期时行比对，结果如表1所示。

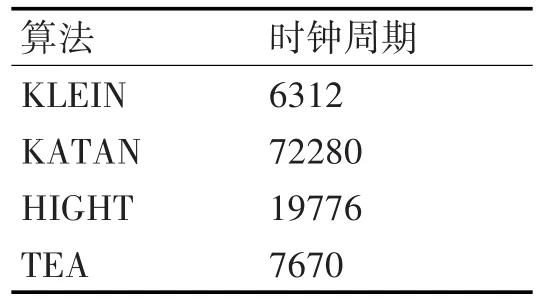
表1 各算法占用的CPU时钟周期

由表中数据可以看出，KLEIN算法占用的时钟周期最少，KATAN算法占用的时钟周期最多。

4.3 能量消耗分析

为了计算各算法执行过程中的能量消耗，假设每个CPU时钟周期的能量消耗不变，利用以下公式进行计算：

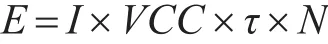
其中，I是消耗的平均电流值，VCC是系统电源电压，τ是每个时钟周期的时间，N是时钟周期数［9］。计算结果如图8所示。

图中能量单位为微焦耳，由图中对比可以看出，KATAN算法消耗了最多的能量，并且与其它算法相比，能量值高出很多。KLEIN算法虽然代码长度最长，但却是消耗能量最少的算法。由此可以得出，相比于代码长度，耗费的CPU时钟周期对能量消耗值的影响更加显著，或者可以说算法实现过程中所体现出来的性能更多地依赖于算法采用的结构，循环次数以及运行的时钟周期数。例如，同一个算法采用不同的迭代轮数，最终的能量消耗也不同。

算法各组件实现的指令也是一个很重要的度量标准。每一个指令运行的时钟周期都不同，为了有效降低算法的能量消耗，在编写代码时选取最适合本算法的指令运行方式非常重要。同时，算法的运行结构也不能忽视，因为不同的结构占用的时钟周期也有较大的差异，例如Feistel和SPN网络结构就存在很大的不同，这些不同将直接对算法的主循环次数产生影响。

5 算法安全性分析

本节用扩散和混乱的程度对算法的安全性进行分析，针对分组密码体制，可以通过统计非线性扩散程度来对算法的扩散和混乱程度做出一个概率上的估计，通过两种程度的对比对算法的安全性进行分析［10］。

5.1 扩散程度

扩散程度是对算法安全性进行分析时的一个重要因素，为了得到更加可靠的分析结果，本文使用一串随机的明文，其它的明文全部由此明文得到。首先保持其它比特位不变，对明文的前20比特逐个进行单比特改变，也就是每个加密的明文与初始明文相比只改变了一个比特位，每一步输出的密文进行异或运算，最终构造出一个20×64的矩阵，对矩阵中“1”的个数所占百分比进行计算，结果如表2所示。

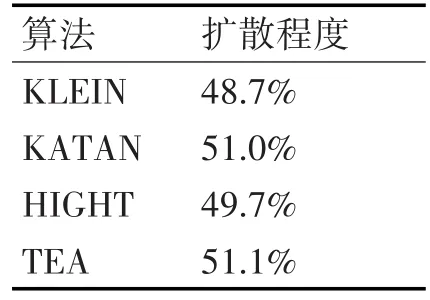
表2 各算法扩散程度测试

5.2 混乱程度

混乱特性可以让明文和密文间的统计关系变得复杂，从而增加算法破译的难度。对混乱程度进行测试时，输入的明文长度为64bits。首先确定一个初始密钥，随后使用的密钥都由初始密钥变化得到。每一次加密都只改变初始密钥的一个比特位，对每一轮加密的输出进行异或运算，最后对所有输出统计结果中“1”的个数所占百分比进行计算，如表3所示。

表3 各算法的混乱程度测试

算法的结构是影响算法安全性的一个重要因素，从以上扩散和混乱特性中的分析可以得出，KLEIN算法的扩散程度最低，而混乱程度最高。由前文的介绍中可知，KLEIN算法采用的是SPN网络结构，而其它三种算法都采用的是Feistel结构，结构的不同导致了KLEIN算法在扩散和混乱特性上的不同。

6 结语

从以上的研究中可以得出，算法的代码分析所得出的结果与算法实现后的结果有一定的差异，并不是代码最简单的性能最好，算法在实现过程中所表现出来的性能更多是受算法的结构，循环的次数以及各指令函数的复杂程度的影响，仅仅靠对代码进行分析是不能对算法的实际性能做出正确评估的。但两者之间又是相互联系，相互制约的，算法所表现的不同性能都可以通过代码之间的比对找到解释的方法，例如，从以上的对比中可以得出算法代码中各组件的指令函数是影响算法性能的一个重要因素，所以，结合算法实际性能对比所得出的结果又可以对算法的代码进行改进，选用更合适的函数完成相同的指令，从而使代码更加地合理完善。

［1］Kardas S，Celik S，Yildiz M，et al.PUF-enhanced offline RFID security and privacy［J］.Journal of Network and Computer Application，2012，35：2059-2067.

［2］黄玉兰.基于物联网的RFID电子标签研究进展［J］.电讯技术，2013，53（4）：522-529.HUANG Yulan.Research progress of RFID tag based on Internet of things［J］.Telecommunication Engineering，2013，53（4）：522-529.

［3］周世杰，张文清，罗嘉庆.射频识别（RFID）隐私保护技术综述［J］.软件学报，2015，26（4）：960-976.ZHOU Shijie，ZHANG Wenqing，LUO Jiaqing.Review of radio frequency identification（RFID）privacy protection technology［J］.Journal of software，2015，26（4）：960-976.

［4］李浪，刘波涛，邹祎，等.KLEIN加密算法优化研究［J］.计算机应用研究，2015，32（3）：877-880.LI Lang，LIU Botao，ZOU Yi，et al.Research on Optimization of KLEIN encryption algorithm［J］.Computer Application Research，2015，32（3）：877-880.

［5］刘爱森.KATAN算法相关密钥的条件差分分析［D］.济南：山东大学，2014：34-50.LIU Aisen.Conditional difference analysis of KATAN algorithm related key［D］.Jinan：Shandong University，2014：34-50.

［6］郭建胜，崔竞一，潘志舒，等.HIGHT算法的积分攻击［J］.通信学报，2016，37（7）：71-78.GUO Jiansheng，CUI Jingyi，PAN Zhishu，et al.Integral attack of HIGHT algorithm［J］.Journal of communication，2016，37（7）：71-78.

［7］李继中.密码算法识别与分析关键技术研究［D］.郑州：解放军信息工程大学，2014：20-25.LI Jizhong.Research on Key Technologies of identification and analysis of cryptographic algorithms［D］.Zhengzhou：ThePLA Information EngineeringUniversity，2014：20-25.

［8］Eisenbarth T，Gong Z，Tim G，et al.Compact Implementation and Performance Evaluation of Block Ciphers in ATtiny Devices［C］//Progress in Cryptology-AFRICACRYPT 2012.Springer Berlin Heidelberg，2012：172-187.

［9］Roy D，Datta P，Mukhopadhyay S.A New Variant of Algebraic Attack［J］.Communications in Computer and Information Science，2014，420：211-222.

［10］ Bogdanov A， Rechberger C. A 3-Subset Meet-in-the-Middle Attack：Cryptanalysis of the Lightweight Block Cipher KTANTAN［C］//In：Biryukov A，GONG Guang，Stinson D R.LNCS 6544：Selected Areas in Cryptography，Berlin：Springer Berlin Heidelberg，2011：229-240.

Implementation and Evaluation of Lightweight Algorithms for RFID

YU Junhe1HOU Wenrui2XU Mingze3
（1.Naval Marine Academy，Guangzhou 510430）（2.Naval Staff，Beijing 100841）（3.College of Science，Naval University of Engineering，Wuhan 430033）

With the rapid development of RFID technology，the security problem is becoming more and more serious.In this paper，combined with the characteristics of RFID system，the HIGHT，KLEIN，TEA and KATAN algorithms which are widely used in RFID are analyzed and compared.Firstly，the assembly code of these algorithms is analyzed，and the time consuming of related operation and instruction set is determined.Subsequently，these algorithms are implemented on AVR MCU，and the security of the algorithm is compared with the aspects of energy consumption，diffusion and confusion.Finally，all the results are compared，and the difference between the code analysis results and the actual implementation results is pointed out.The research results of this paper not only reveal the different performance of the algorithm，but also show that the results of the algorithm and the results of the code analysis are quite different.

RFID，lightweight algorithm，simulation

TP301

10.3969/j.issn.1672-9722.2017.11.008

Class Number TP301

2017年5月8日，

2017年6月24日

于钧合，男，硕士研究生，助理工程师，研究方向：信息安全。侯文瑞，男，助理工程师，研究方向：网络安全。徐铭泽，男，研究方向：信息安全。