非绝热壁面边界在离心压气机数值模拟中的应用

吴东润，滕金芳，羌晓青，马 威

非绝热壁面边界在离心压气机数值模拟中的应用

吴东润，滕金芳，羌晓青，马 威

（上海交通大学，上海 200240）

随着离心压气机级负荷与温升水平的提高，为了提升对离心压气机的数值模拟精度，在数值模拟中需要采用非绝热壁面边界条件。本文以一台设计良好的现役离心压气机为研究对象，对其数值模拟的壁面边界条件中分别应用了绝热壁面边界条件，以及等温和给定传热系数这两类常用的非绝热壁面边界条件，对比分析了非绝热壁面边界条件对数值模拟精度的影响及其原因。采用给定传热系数壁面边界条件的数值模拟结果中，效率计算误差最小，设计点效率误差较绝热计算下降46.6%，且计算结果对传热系数偏差有一定容忍度；产生上述差异的原因主要源于叶顶损失相关计算。采用等温壁面边界条件的设计点数值模拟结果中，参考温度偏差使等温边界相比绝热边界效率计算误差增大93.2%，说明等温边界对参考温度敏感，其进一步应用需依靠更精确的参考温度。

离心压气机；数值模拟；非绝热边界；传热效应

1 前言

压气机数值模拟中，绝热壁面边界即假设叶片、轮毂和外机匣壁面无热流的边界条件。绝热壁面边界设置简单，当近壁面处传热过程不显著时具有较好的计算精度，因此广泛地应用于压气机数值模拟中。但由于忽略了壁面非绝热过程的影响，绝热壁面边界模拟壁面传热显著的模型时计算结果将不能满足精度需求，例如模拟压气机功率与壁面传热量相近、工作环境温度分布不均匀等工况结果较差。非绝热壁面边界假设壁面有热流通过，该假设相较绝热壁面边界更接近真实过程，尤其在壁面传热显著的情况下。已有研究针对上述壁面传热显著的工况应用非绝热壁面边界，并获得了更好的模拟结果［1～7］。

目前随着离心压气机的发展，单级压比急剧增加，进而温度梯度也急剧增加。比如最新设计的单级离心压气机［8］，其压比已经达到5.2，总温比已经超过1.75。更严峻的问题是，由于离心叶轮出口宽度最窄，传热效应最为显著。因而对高性能离心压气机的数值模拟中，采用无壁面传热的绝热壁面边界条件的数值模拟结果精度较低，不能满足对离心压气机设计和流动机理研究的需要。为了提高对高性能离心压气机的数值模拟精度，需要设置与真实流动更接近的非绝热壁面边界条件。但是非绝热壁面边界条件对离心压气机数值模拟精度的影响以及其物理机理目前还不是很清楚，需要进行深入的研究。特别是高压比离心压气机做功能力强，非绝热边界条件在传热量与功率比值不显著时的作用尚未充分研究。

本文以一台设计良好的现役离心压气机为研究对象，对其数值模拟的壁面边界条件中分别应用绝热壁面边界条件，以及等温和给定传热系数这两类常用的非绝热壁面边界条件，对比分析非绝热壁面边界条件对数值模拟精度的影响及其原因。

2 研究对象与数值方法

2.1 研究对象

研究的对象为跨音速单级离心压气机（Ro lls-RoyceDDA404-III改进型），其结构如图1所示，主要结构与热态性能参数如表1所示［12］。该离心压气机由带分流叶片的离心叶轮和有叶扩压器组成，应用于卡车/汽车和电站中先进的燃气轮机再循环技术等领域。该型号离心压气机单级温比达1.6，压气机内部流体温度梯度显著，适合作为非绝热边界条件的详细研究对象。研究人员对该模型进行了大量的实验研究［9～11］。

图 1RRDDA404-III改进型离心压气机结构示意

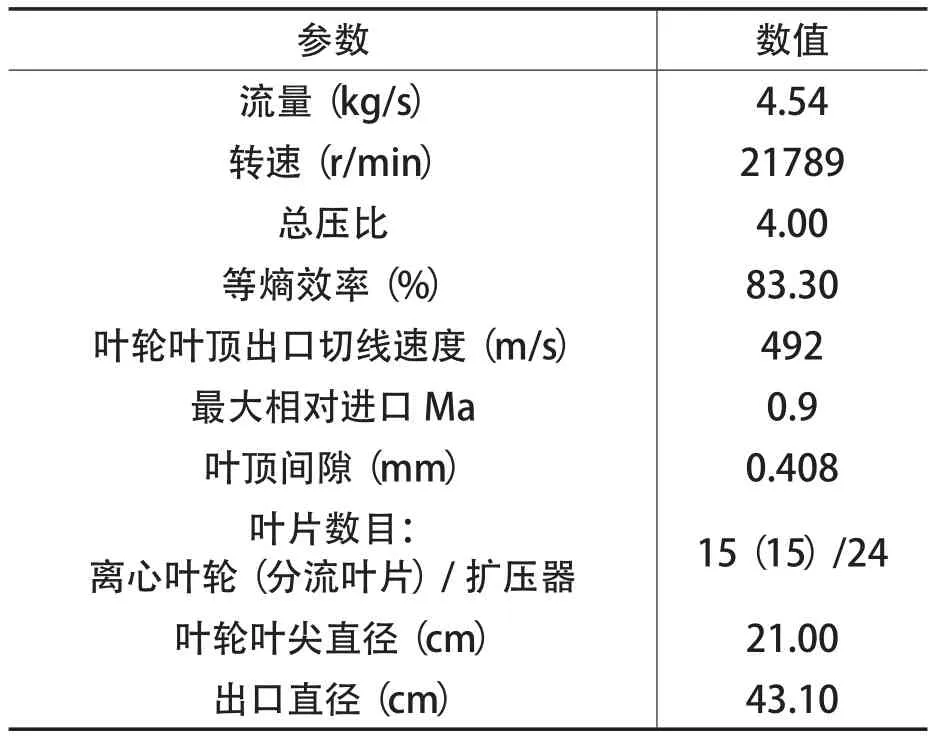
表1 RR DDA 404-III改进离心压气机型热态设计性能、结构参数

2.2 数值方法

采用NumecaIGG/Autogrid组件对Rolls-RoyceDDA404-III改进型离心压气机划分结构化网格，离心叶轮采用O4H拓扑结构，有叶扩压器采用HOH拓扑结构，网格总数约为180万。采用Num eca/Fine组件进行定常RANS数值计算，湍流模型选用S-A模型。进口给定总温、总压和速度方向，出口按径向平衡方程给定平均半径处的静压。

处理固体壁面时，分别采用绝热和非绝热壁面边界。非绝热壁面边界采用给定传热系数和等温两类最通用的给法，给定传热系数法已在以往的研究中大量应用，其效果有较好评估［12］。等温壁面的处理方式还可参考文献［4，5，13，14］。

采用等温或对流换热系数壁面边界条件时，本文参考了相同进出口边界条件下绝热计算的结果给定参考温度，以保证采用新计算边界后其结果具有可比性。等温壁面边界条件可分轮毂、外机匣和叶片3部分给定，其中叶片还应区分吸力面和压力面。对于轮毂和外机匣，其表面的参考温度分布直接选取了绝热计算的固壁面静温周向平均值。为合理给定叶片表面参考温度，本文首先讨论了绝热计算的叶片表面静温分布，其绝热计算结果如图2所示。由图中可见，离心叶轮的叶片表面静温分布与径向位置相关，有叶扩压器表面静温分布较均匀。根据离心轮的加功与增压原理可知，径向位置很大程度决定了增压的程度，而增压程度与叶片表面温度密切相关，因此本文假设非绝热壁面参考温度与径向位置相关，忽略了其在不同叶高或轴向位置可能产生的差异，具体取值选为绝热计算50%叶高的结果。这一假设仅在离心叶轮压力面近尾缘处（图2b）和有叶扩压器前缘处（图2c）误差稍大。

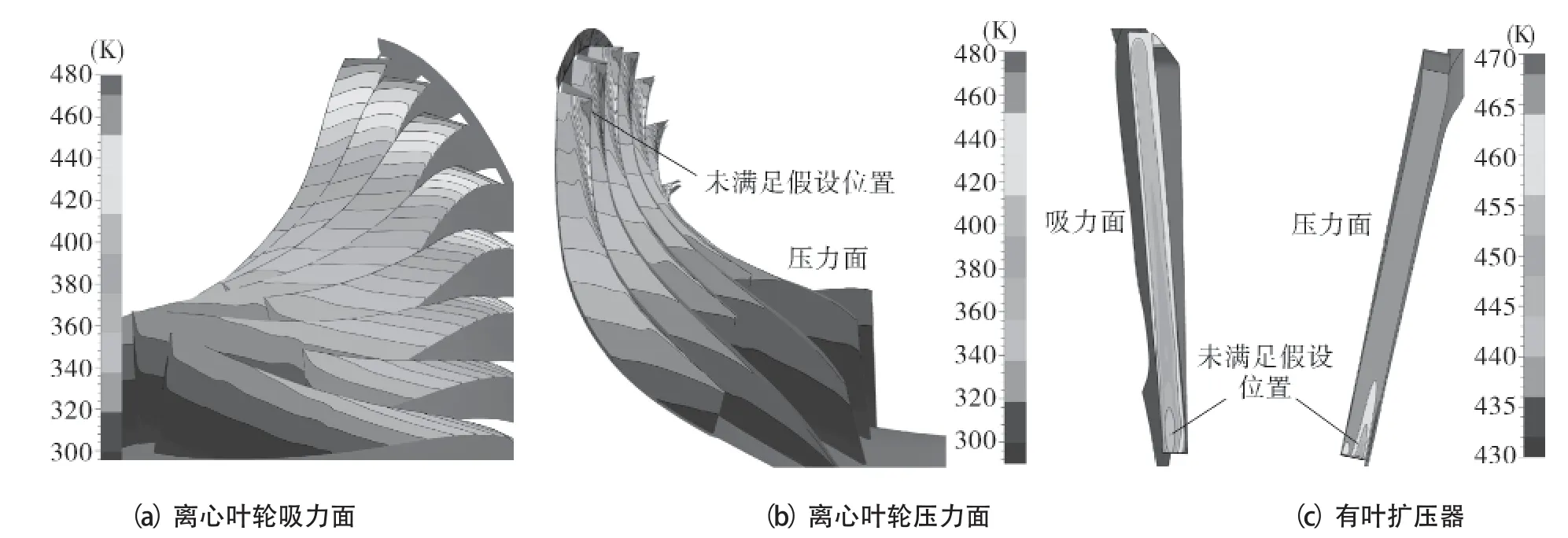
图2 各排叶片表面静温分布

当壁面给定传热系数时，其参考温度参照了绝热计算结果，由于压气机固壁金属的Bio t数小于0.01，分别对各排叶片轮毂、外机匣及叶片吸、压力面给定均值［4，5］。除此以外，该方法还要考虑传热系数取值的影响，具体值将在后文分析中进行讨论。

2.3 非绝热壁面传热量的热力学影响

在讨论非绝热壁面边界条件计算结果前，必须明确传热将引起热力学影响和动力学影响，其中热力学影响需要单独列出讨论，方法可参照以往研究结果［3］。为此，表2分别给出了各非绝热壁面数值模拟结果在设计点时的壁面传热量。由表2可知，给定较大的固壁面换热系数或等温条件时，壁面存在较强的换热现象。为量化传热热量带来的热力学效应，采用固壁传热的微型压气机模型的定义［3］：

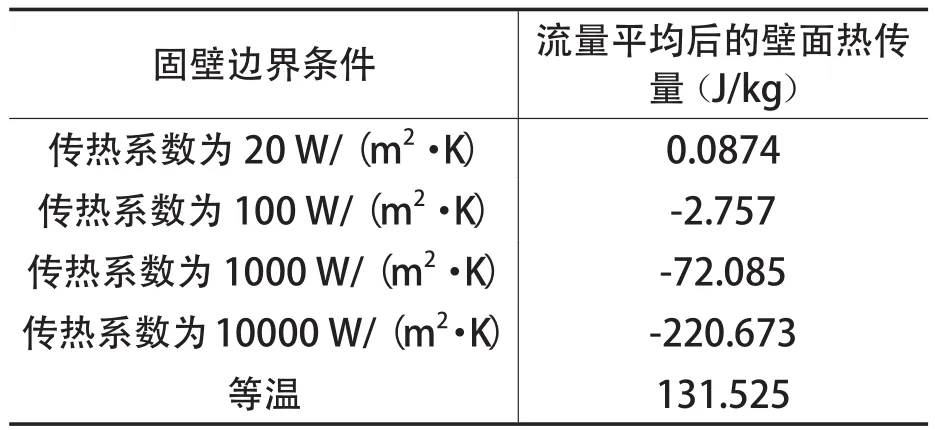
表2 各非绝热固壁条件下壁面传热量

式中QH——传热量与总焓之比

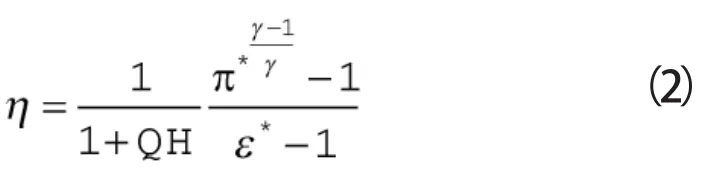
式中η ——考虑非绝热壁面传热的效率

式（2）隐含两条假设，即假设非绝热过程是进口的等压传热与绝热增压过程的叠加，且这一绝热增压与绝热过程具有相同效率［2，3，6］。

针对本文模型，进口总焓hin取292kJ/kg，QH最大值约为0.075%，对应传热系数为10000。故本文壁面传热量远小于整机功率量级，而以往微型燃机的研究模型其传热量可达整机功率25%～80%［3］。本文模型适合于研究传热量与功率比值不显著时非绝热壁面的作用。

γ ——比热比

3 计算结果与讨论

3.1 总特性

通过改变出口背压条件，由堵塞点逐渐增加背压计算，获得了绝热和给定传热系数壁面边界设计转速流量特性曲线，设计流量的流量系数中取1，如图3所示。图中还给出了设计点附近采用等温和不同传热系数的计算结果。等温计算效率在设计点已远离真实值，故图中不再给出等温壁在全工况的计算结果。结果表明：喘振裕度和设计点右支特性线计算误差最显著，且绝热和给定传热系数壁面边界条件下的设计点右支结果基本重合，说明特性线右支非绝热壁并未对流动计算产生显著影响,2种方法的设计点左支总压比计算结果接近，但由于计算近喘点流量值小于试验值，最大相对误差发生在试验近喘点，约为1.32%（忽略近喘点外的计算点，下同）；对于效率计算，绝热特性线左支最大相对误差发生在流量系数φ=0.97附近，约为1.61%，给定传热系数时左支效率最大相对误差发生在设计点，约为0.73%。

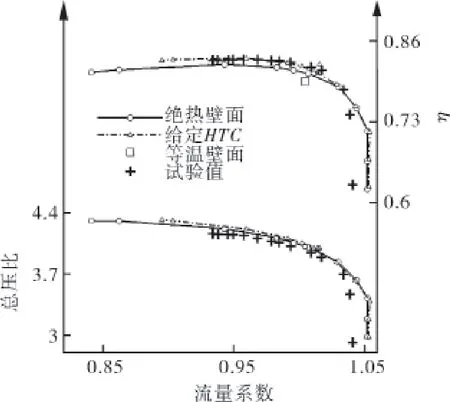
图3 效率总压比特性线

各计算点的效率在图4中放大绘出。设计点传热系数（HTC）取值范围在20～10000内，给定HTC计算相较绝热计算更接近试验结果，且当HTC取值在20～1000时计算结果接近，最终选取了HTC=1000并计算了对应的特性线。设计点绝热计算效率误差1.33%，HTC=1000时效率误差0.71%，误差下降46.6%。而等温壁面边界条件时计算结果远低于试验值，效率误差2.57%，相对绝热计算增长93.2%，下文的损失讨论中将论述原因。

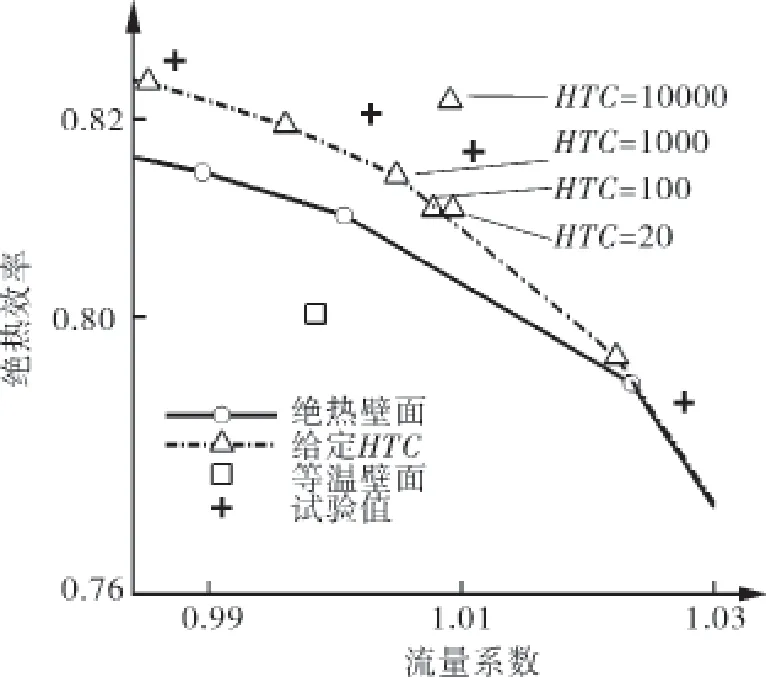
图4 近设计点效率特性

3.2 主流流动

为了解数值计算对流场的还原程度，本文选取了离心叶轮主叶片1%、30%和99%弦长作为特征位置讨论其速度分布，其中30%弦长位于分流叶片前缘。以70%和90%叶高的无量纲子午速度沿叶片间距的分布评价主流的流动情况，如图 5 所示。

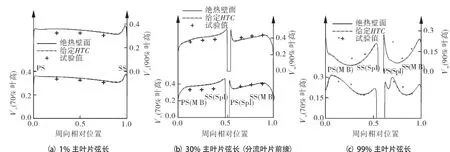
图5 各弦长子午速度沿流道分布

PS.压力面；SS.吸力面；MB.主叶片；Sp l.分流叶片

详细试验数据可见文献［11］，其相对误差小于2%。在此给出无量纲子午速度Vm的定义：

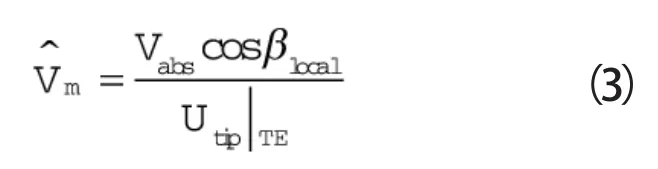
式中Vabs——绝对速度

βlocal——当地气流角——叶顶尾缘切线速度

当壁面边界条件为绝热或给定传热系数时，主叶片与分流叶片前缘截面各叶高子午速度的数值计算结果皆与试验结果吻合较好。主叶片前缘处（图5（a）），吸力面附近的子午速度突增，通道截面由压力面至吸力面速度略有递减的流动过程还原较为准确。分流叶片前缘（图5（b））子午速度沿主叶片压力面向主叶片吸力面子午速度的增长也较好地符合了试验结果与实际分布规律。

从图可见，计算结果仅在尾缘（99%弦长）90%叶高部分位置存在一定差异（图5（c））。根据Hathaw ay的研究结果，叶轮尾缘94%弦长与99%弦长的速度分布规律发生了显著变化，通道内叶顶附近子午速度的线性增长被凹形分布替代，本文的数值计算结果与对应99%弦长处的凹形分布较为相似［15～19］。考虑到99%弦长试验测点距离叶片出口十分接近，该位置在尾缘处的速度变化又较为剧烈，其测量值与数值结果可能在部分位置存在一定偏差。

通过对离心叶轮不同位置的流动计算结果讨论，可知本文数值模拟结果具有一定程度的可信度。绝热计算结果与给定传热系数结果可知壁面边界条件的改变并未对主流流动过程产生显著影响。

3.3 损失

上文计算得到的特性线说明绝热计算与给定传热系数计算结果在效率结果上存在显著差异，在此以子午流向熵梯度作为评估流道损失的主要参数讨论损失计算差异来源，其定义为：

图6给出了设计点97%叶高的子午流向熵梯度分布，2种边界条件计算的主要差异体现已在图中分别标识。区域1为叶轮前部的分流叶片叶尖位置，给定传热系数边界计算时该处熵梯度略有增加。而在叶轮中后部的区域2，3和4中，给定传热系数边界计算的熵梯度出现了明显的下降，尤其是主叶片和分流叶片尾缘叶顶附近高熵梯度区范围减小。以上结果表明，给定传热系数计算在叶轮前部和后部引起的性能变化是不同的。为探究性能变化的原因，应对壁面的换热过程进行进一步讨论。

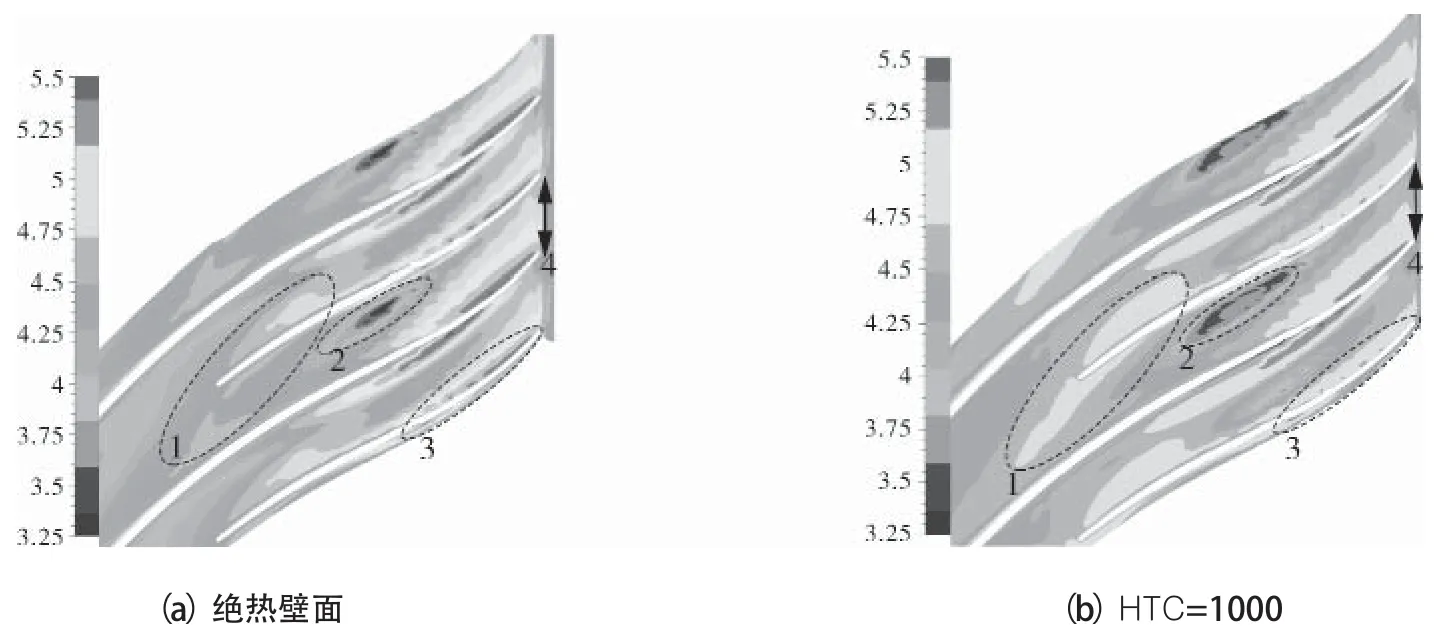
图6 97%叶高子午流向熵梯度云图

图7 给出了3种边界条件计算及试验条件下离心轮的总温升结果。

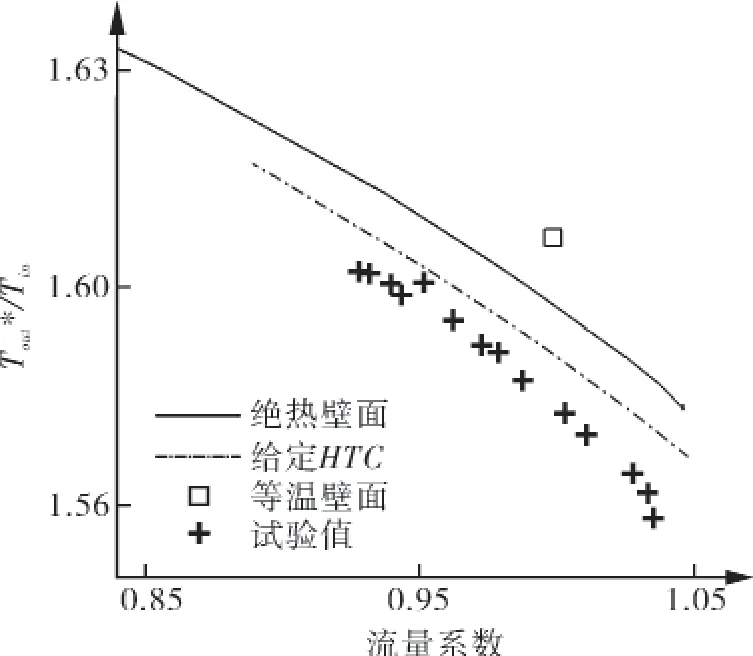
图7 总温升特性线

结果显示相比绝热计算，给定传热系数时的总温升计算结果向试验结果接近，设计点总温升误差因此下降33.8%，而等温壁面的结果则远高于相同流量下其他方法的计算值，误差相较绝热计算增加70.6%。这是由于等温边界计算时，壁面存在极强的换热能力，而通过绝热计算获得的壁面参考温度偏高，导致等温计算中热量注入流道，使流体总温升进一步增大。由于相同做功能力下计算温升与计算损失正相关，图7与上文特性线和熵梯度结果保持了一致。

图8还给出了绝热及给定传热系数2种壁面边界在叶片前、尾缘80%叶高以上的周向平均静温分布。结果表明给定传热系数计算在离心叶轮前部端壁温度高于绝热计算值，尾部端壁温度低于绝热计算值，故绝热计算静温升远高于给定传热系数结果。该结果还可以解释图7中2种计算条件在叶轮前后熵梯度结果出现的差异。给定传热系数计算中沿流向既存在前部低温流体向高温壁面吸热的过程，也存在后部高温流体向低温壁面放热的过程，因此在叶轮前部出现了熵梯度的增加，而在叶轮后部尤其是叶轮尾缘减少了叶顶附近的熵梯度，使得高熵梯度的范围下降。且由图7可知，给定传热系数计算总温升更接近试验值。相对其他两种计算边界，给定传热系数的壁面边界理论上对近壁面热量传递的模拟最接近真实过程，证明了该类非绝热计算边界条件的有效性。

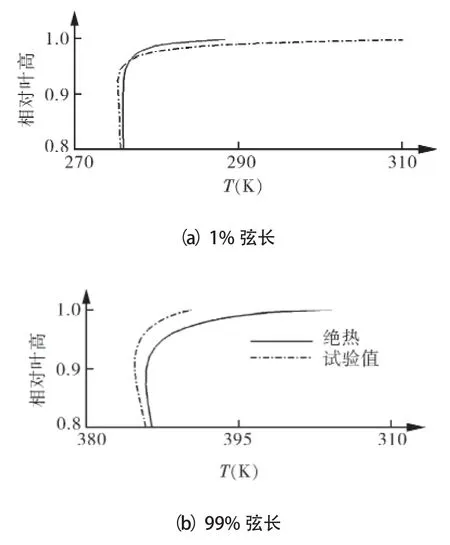
图8 离心叶轮周向平均静温分布

4 结论

（1）绝热壁面边界与给定传热系数壁面边界条件主流计算结果一致，表明给定传热系数边界条件影响范围主要在近壁面处。

（2）壁面边界条件为给定传热系数时数值模拟误差最小。该方法在叶顶处计算损失显著减小，叶顶静温升显著下降，计算总温升和效率特性最接近真实值，相较绝热计算，HTC取1000时设计点效率计算误差减少46.6%，设计点总温升计算误差减少33.8%。

（3）等温壁面边界条件数值模拟结果中，设计点数值模拟偏差显著增大，效率误差增大93.2%。设计点计算壁面传热偏离真实过程，误差相较绝热计算增加70.6%。给出更精确的参考温度是合理使用该类方法的前提条件。

［1］ ISOMURA K，MURAYAMA M，KAWAKUBO T. Feasibility Study of a Gas Turbine at Micro Scale ［C］. ASME 2001-GT-0101.

［2］ 龚建波，林峰，徐纲，等. 非绝热小燃机热力学模型分析［J］. 工程热物理学报，2009，30（10）：1643-1647.

［3］ GONG Y，SIRAKOV B T，EPSTEIN A H，et al. Aerothermodynamics of micro turbo- machinery ［C］. ASME 2004-GT-53877.

［4］ 沈煜欣，刘建军. 考虑热传导的微型离心压气机设计与数值分析［J］. 航空动力学报，2010，25（4）：897-901.

［5］ RIBAUD Y. Internal heat mixing and external heat losses in an ultra micro turbine ［C］. Tokyo：Proceedings International Gas Turbine Congress，2003.

［6］ BOHN D，HEUER T，KUSTERER K. Conjugate flow and heat transfer investigation of a turbo charger：part i-numerical results ［C］. ASME 2003-GT-38445.

［7］ SHAABAN S. Experimental Investigation and Extended Simulation of Turbocharger Non-Adiabatic Performance ［D］. Hannover：University Hannover，2004.

［8］ 张学锋，卢新根，韩戈，等. 高压比离心压气机设计及试验验证 ［J］. 燃气轮机技术，2014，27（4）：31-36.

［9］ SKOCH G J，PRAHST P S，WERNET M P，et al. Laser anemometer measurements of the flow field in a 4：1 pressure ratio centrifugal impeller［C］. ASME 1997-GT-342.

［10］ 贺晓亮. 跨音速离心压气机三维流场数值分析［D］. 哈尔滨：哈尔滨工程大学，2010.

［11］ SKOCH G J. Experimental investigation of centrifugal compressor stabilization techniques［C］. ASME 2003-GT-38524.

［12］ MCKAIN T F，HOLBROOK G J. Coordinates for a high performance 4：1 pressure ratio centrifugal compressor ［R］. NASA CR-204134.

［13］ CHEW J W，HILLS N J. Computational fluid dynamics for turbomachinery internal air systems［J］. Philosophical Transactions of the Royal Society A：Mathematical，Physical and Engineering Sciences，2007，365（1859）：2587-2611.

［14］ SHAH P N. Novel Turbomachinery concepts for highly integrated airframe/ propulsion systems ［D］. Cambridge，MA：Massachusetts Institute of Technology，2007.

［15］祝华云，徐志明，胡国军，等.尾缘厚度对压气机叶栅气动性能的影响研究［J］.机电工程，2016，33（2）：187-190.

［16］任俊明，王威，张有华.浅析高温热油液力透平机械密封［J］.化工设备与管道，2015，52（6）：55-58.

［17］阳大清，周红桃.绕管式换热器壳侧流场流动与传热数值模拟研究［J］.压力容器，2015，32（11）：40-46.

［18］赵泽霖，焦光伟，周建庭，等.基于土弹簧模型的埋地输油管道地震响应数值模拟［J］.压力容器，2014，31（11）：50-55.

［19］ Hathaway M D，Chriss R M，Wood J R，et al. Experimental and computational investigation of the nasa low-speed centrifugal compressor flow field ［R］. NASA TM-4481.

Application of Non-adiabatic Wall Boundary Condition in Numerical Simulation for Centrifugal Compressor

WU Dong-run，TENG Jin-fang，QIANG Xiao-qing，MA Wei
（Shanghai Jiaotong University，Shanghai 200240，China）

With the improvement of stage load and temperature level of centrifugal compressor，in order to improve numerical simulation accuracy of centrifugal compressor，it’s necessary to study the influence of non-adiabatic boundary condition on numerical simulation. In this work，numerical simulation of a well-designed active centrifugal compressor was carried out. Adiabatic and two widely used non-adiabatic boundary conditions，isothermal and heat transfer coefficient （HTC） imposed boundary conditions were employed. Numerical accuracy of non-adiabatic simulation was analysed in detail. Simulation with HTC imposed boundary condition reduces 46.6% of error in efficiency at design point，in despite of the deviation of the HTC in a certain range. Detailed analysis shows that main difference between HTC imposed and adiabatic boundary conditions comes from tip loss related simulation. Numerical simulation with isothermal boundary condition shows that the efficiency error raises 93.2% compared with adiabatic results because of the deviation of the reference temperature. Isothermal boundary condition is sensitive to the reference temperature，and thus the selection of reference temperature should be carefully considered in further study.

centrifugal compressor；numerical simulation；non-adiabatic boundary；heat transfer effect

TH452

A

10.3969/j.issn.1005-0329.2017.11.008

1005-0329（2017）11-0041-06

2016-10-25

2016-12-02

吴东润（1993－），男，博士研究生，专业方向为叶轮机械气动热力学，通讯地址：200240上海市闵行区东川路800号上海交通大学航空航天学院，E-m ail：vanderain@sjtu.edu.cn。