不同叶片出口角下离心泵压力脉动及径向力分析

张忆宁，曹卫东，姚凌钧，姜 昕

不同叶片出口角下离心泵压力脉动及径向力分析

张忆宁，曹卫东，姚凌钧，姜 昕

（江苏大学国家水泵及系统工程技术研究中心，江苏镇江212013）

在试验结果和数值模拟吻合良好的基础上，开展叶片出口角对离心泵压力脉动以及径向力影响的研究。本文以两级矿用潜水离心泵为研究对象，建立4组不同叶片出口角叶轮模型，通过数值模拟获得离心泵外特性，叶轮、导叶、蜗壳的压力脉动分布及叶轮径向力特性，并进行对比分析。结果表明：离心泵内压力脉动呈周期性，当β2=16°和20°时叶轮出口压力脉动强度较大。随着叶片出口角增大，导叶和蜗壳内压力脉动均逐渐增强，且导叶内压力脉动强度大于蜗壳，不同叶片出口角下，导叶及蜗壳内脉动主频均为叶频。叶片出口角的改变也会对叶轮径向力矢量分布产生一定影响，随着β2增大，叶轮径向力逐渐增大，且首级叶轮轴向力大于次级叶轮，蜗壳比导叶有更好地改善叶轮轴向力的作用。

离心泵；数值模拟；叶片出口角；压力脉动；径向力

1 前言

多级离心泵因其扬程高的特点被广泛应用于农业灌溉、电力化工及矿山等领域。在离心泵运行过程中，叶轮与导叶或叶轮蜗壳的干涉作用引起泵内部压力脉动，是影响离心泵稳定运行的主要原因［1～3］。为提高离心泵运行效率以及稳定性，需系统地研究其内部压力脉动规律。目前，国内外对离心泵内部非定常压力脉动特性展开了相关研究，主要通过试验以及数值模拟来实现［4～6］。张德胜等对多工况轴流泵压力脉动进行了试验研究，揭示了轴流泵内不同位置压力脉动规律［7］。袁寿其等研究了非设计工况下时序效应对离心泵内压力脉动的影响，得出导叶时序效应对离心泵内压力脉动强度影响较明显［8］。曹树良等研究了旋转叶轮区流动特性，不同工况下叶片脉动主频均为叶频，压力脉动强度由进口至出口逐渐增大［9］。江伟等分别研究了导叶与隔舌相对位置、蜗壳进口变对离心泵径向力的影响，为改善离心泵径向力提供了一定思路［10，11］。刘厚林等模拟了四种导叶轴向位置角α下整泵流场，得出随α增大，径向力脉动幅值先增大后减小［12］。Zhang等研究了导叶式离心泵中叶片数和导叶数对内部流动的影响，当叶片数和导叶数相同时压力脉动较小，反之较大［13］。AkinoriFu rukaw a等研究了叶轮出口至导叶的压力脉动，表明叶轮与导叶的相互干涉比叶轮尾迹对导叶内压力脉动作用更为明显［14］。Guo等以高扬程泵为对象，研究大流量偏工况下压力脉动，得出导叶高压区流道振幅大于低压区［15～21］。

本文以两级矿用潜水离心泵为对象，基于CFX软件对离心泵内部非定常压力脉动进行数值计算，对每级压力脉动规律进行研究，分析内部流动规律及作用于叶轮上的径向力特征，为离心泵的稳定运行，提供一定参考。

2 流场计算

2.1 计算模型

以两级矿用潜水离心泵为研究对象，其设计参数为：流量Q=25m3/h，单级H=75m，额定转速n=2900r/m in，比转数ns=34。主要过流部件参数分别为：叶轮进口直径D1=90mm；叶轮出口直径D2=250mm，叶片宽度b2=10mm，叶片数Z=3；首级压水室导叶进口直径D3=260mm，进口宽度b3=14mm；次级压水室为双出口蜗壳，基圆直径D4=260mm，进口宽度b=20mm，出口直径D5=40mm。为研究叶片出口安放角对离心泵压力脉动的影响，在保证叶轮其他参数不变下，将β2分别设计为 12°、16°、20°、24°。

为获得较为稳定的流场计算结果，将进水段和蜗壳出水端适当延长。采用ICEM对计算区域进行网格划分，进水段、叶轮、泵腔采用六面体网格划分，并对近壁区域网格局部加密，而对导叶和蜗壳采用适用性较好的四面体网格划分，计算区域网格划分如图1。

图1 计算区域网格划分

2.2 边界条件设置

定常计算边界条件设置为质量流量进口，并假设进口速度分布均匀，出口设置为opening，并且固体壁面采用无滑移边界条件，壁面粗糙度为0.025mm。采用k-ε湍流模型定常计算结果作为非定常计算的初始条件，设置叶轮旋转一周需360个步长，即叶轮旋转1°为一步，时间步长Δt=5.74713×10-5s，迭代6个旋转周期，设置收敛精度为10-4，取最后一圈计算结果为分析对象。

2.3 监测点设置

为了分析不同叶片出口安放角对离心泵压力脉动的影响，在首级、次级叶轮，导叶，蜗壳中分别设置监测点。其中p11～p13位于首级叶轮靠近其出口处，p21～p23位于次级叶轮的相同位置。d1～d3位于正导叶流道中心线，w1～w8分别位于蜗壳八个断面，g1～g2位于隔舌位置，见图2。

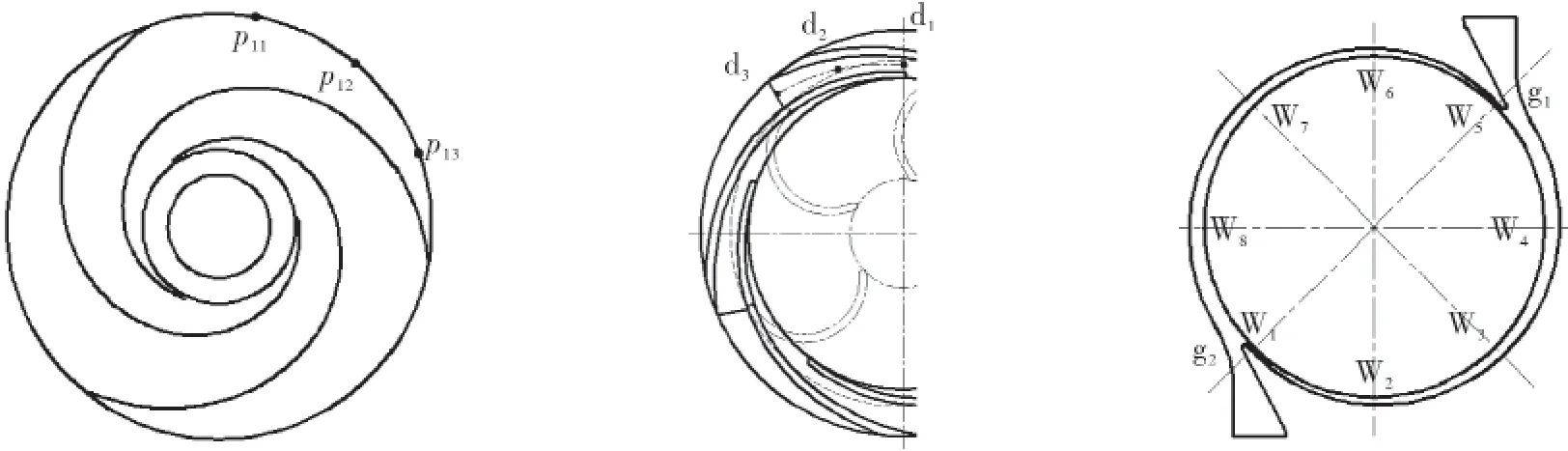
图2 监测点位置

为研究离心泵内压力脉动，引入无量纲参数Cp，即：

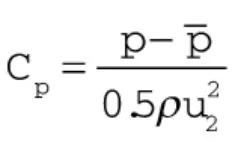
式中p——所在监测点瞬时静压，Pa

ρ——流体密度，kg/m3

u2——叶轮出口圆周速度，m/s

3 离心泵能量特性

为验证数值计算的可靠性，选择叶轮β2=16°的方案进行外特性试验。以常温清水为试验介质，记录流量分别为0.8Q～1.88Q6个工况点的外特性试验数据。试验结果处理时，将潜水电机的效率简化计算为常值88%，试验结果如图3所示。扬程、效率和功率的定常计算结果与试验值在趋势上有高度的一致性，最大相对误差分别为8.7%、8.8%、7.99%，额定工况附近外特性误差均在5%以内。因此，数值计算结果可以用来反映泵内流动状态，为非定常计算奠定了基础。

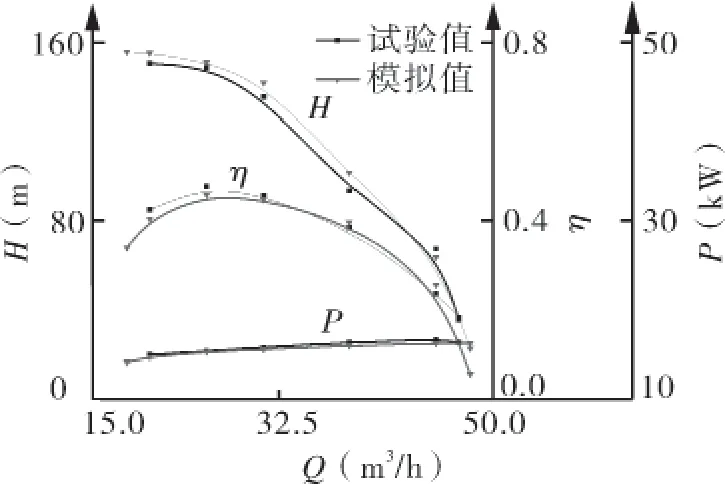
图3 试验性能与模拟性能对比

4 压力脉动分析

4.1 时域分析

由图4可以看出，设计工况下，叶轮出口压力脉动系数呈现周期性变化。图4（a）中，叶轮旋转一周内，p12监测点压力出现5个脉动周期，与正导叶个数相同，说明叶轮和导叶进口的动静干涉是引起首级叶轮出口压力脉动的主要原因。由于叶片数较少，叶轮流道内易出现漩涡，使脉动波形较为复杂，均出现二次波峰，其中β2=16°和20°时的脉动强度明显高于12°和24°。从图5可以看出，随着叶片出口角增大，叶轮出口湍动能逐渐增大，而当β2=24°时，其有所减弱，在次级叶轮中亦如此，由此可见，叶轮出口压力脉动强度和湍动能具有同步相关性。随着叶片出口角增大，叶轮流道变宽，对流体的束缚能力减弱，流道中更易出现漩涡，水力效率降低，因此低比速离心泵叶轮出口角的选择不宜过大。相较首级叶轮，图4（b）中，次级叶轮出口压力变化更为复杂，叶轮旋转一周内，p22监测点压力出现6个波动周期，其中β2=16°和20°时的脉动强度明显高于12°和24°，次级叶轮出口脉动幅值明显小于首级叶轮，说明导叶与叶轮的相互作用远大于蜗壳。由图4（c）可看出，导叶内监测点压力脉动系数呈现一定周期性，一个旋转周期内，d1监测点处出现3个波动周期，数目与叶轮叶片数相同，说明叶轮与导叶干涉作用是正导叶流道内压力脉动的主要原因。其中β2=20°时脉动强度最大，β2=24°时脉动强度最小。受叶片尾部漩涡的影响，导叶进口压力脉动出现二次波峰。

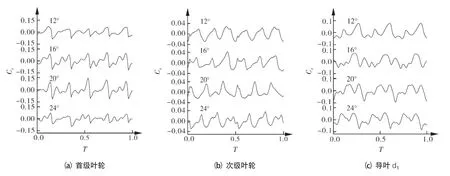
图4 叶轮及导叶压力脉动时域

图5 首级、次级离心泵中截面湍动能分布

图6 （a）为β2=12°时蜗壳不同断面监测点压力脉动，靠近蜗壳隔舌处压力脉动最大，远离蜗壳隔舌压力脉动较弱。w3监测点脉动强度最大，由w3位置可知，其与隔舌位置相对较近，受蜗壳隔舌的影响，此处压力脉动较大。而w4虽与隔舌更为接近，但由于w4处断面面积较小，脉动相应会受到影响。因此，蜗壳内压力脉动强度不仅与监测点和隔舌相对位置有关，也和监测点所在断面面积存在一定联系。图6（b）为不同叶片出口角下蜗壳w3监测点压力脉动，从中可以看出w3监测点压力呈现周期性脉动，均出现3个波动周期。其中，随着叶片出口安放角的增大，w3监测点脉动强度有增大趋势。图6（c）为隔舌压力脉动时域，其中β2=16°和24°时压力脉动较强。

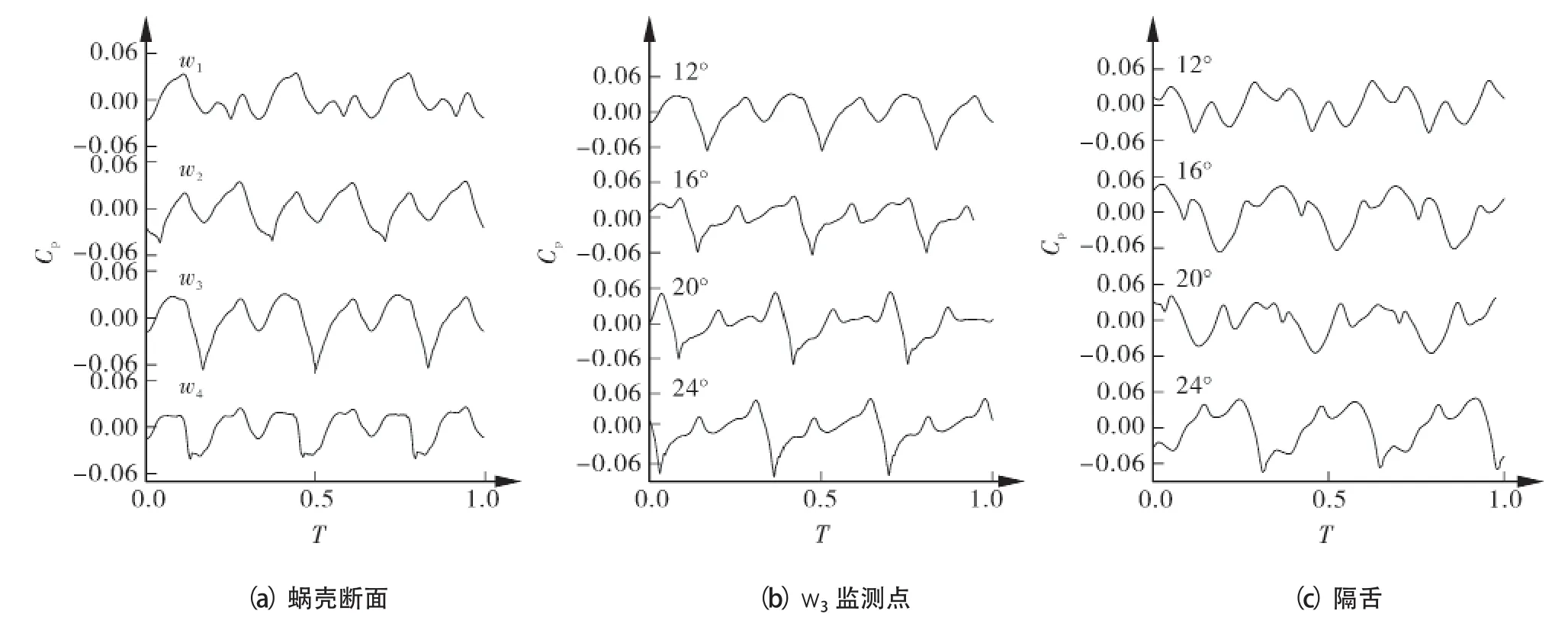
图6 蜗壳内压力脉动时域

由于叶轮中低压高速流和蜗壳中高压低速流的瞬间结合，蜗壳内脉动波形较为复杂，均出现多个波峰波谷，随着出口安放角增大，脉动波形逐渐接近于正弦谐波。

4.2 频域分析

对时域图进行快速傅里叶变化，得出频域分布规律，如图7,8所示。叶轮转速为2900r/m in，轴频率fn=48.33Hz，叶频f=145Hz，图中横坐标为轴频倍数N，Cp为脉动幅值。不同叶片出口角下的首级叶轮脉动主频为5倍轴频（即正导叶频率）及其倍频，次主频为叶频及其倍频，因叶轮叶片掠过导叶叶片时，压力面和吸力面压力的交替变化出现脉动幅值。次级叶轮脉动主频为叶频及其倍频，在2倍叶频时达到最大峰值。导叶d1监测点脉动主频以叶片通过频率为主，在1倍叶频时出现最大脉动幅值，脉动幅值排序为20°＞12°＞24°＞16°。可见，叶轮与导叶的动静干涉是导致叶轮和导叶流道内压力脉动的主要因素。

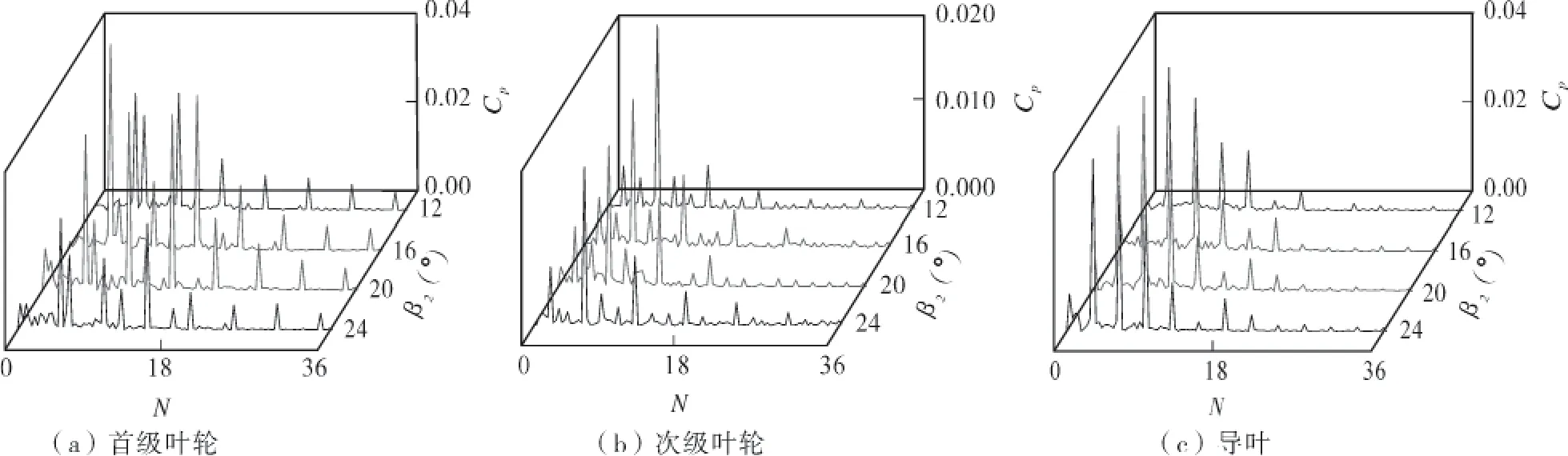
图7 叶轮及导叶脉动频域

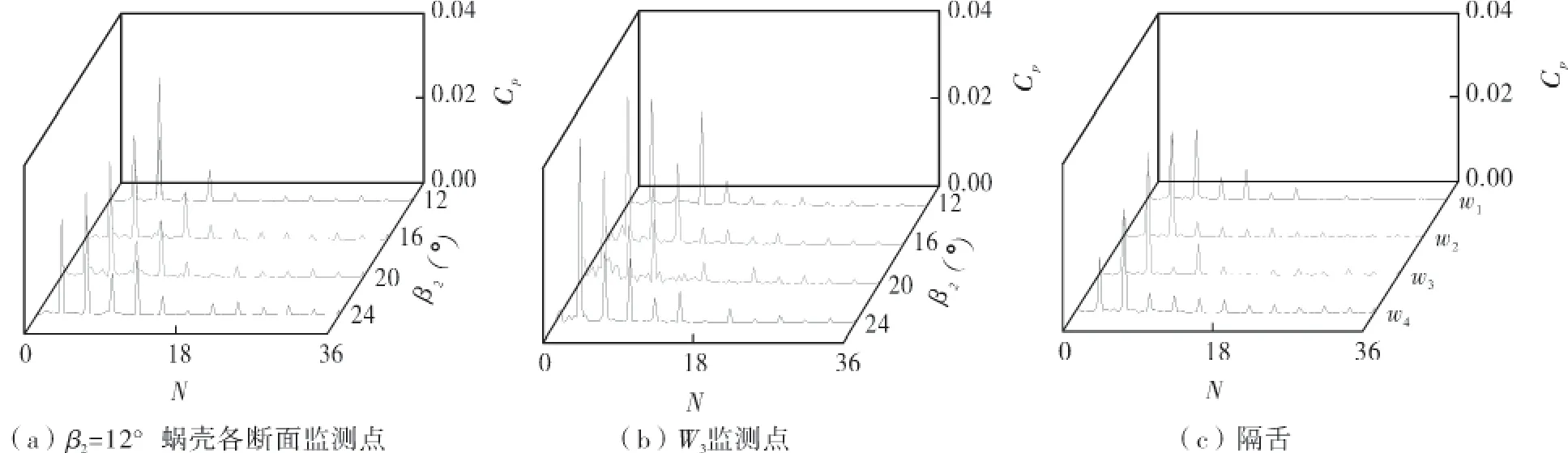
图8 蜗壳脉动频域

在设计工况下，蜗壳各断面监测点脉动主频均为叶频，其中在2倍叶频时，脉动幅值最大，各断面监测点幅值排序为w3＞w2＞w4＞w1。不同叶片出口角下，w3监测点处压力脉动主频均为叶频及其倍频，在2倍叶频处达到脉动峰值，可见叶片出口角对蜗壳脉动主频没有明显影响；叶轮和蜗壳交界面圆周方向上隔舌处压力脉动最大，隔舌处脉动主频为叶频及其倍频，2倍叶频时达到脉动最大峰值。

5 叶轮径向力

图9、10为首级、次级叶轮径向力。叶轮径向力呈周期性变化，随叶片出口角增大，叶轮径向力有逐渐增大趋势，其中首级叶轮相较次级叶轮受力变化更为复杂，可能由于首级叶轮流场不稳定，二次流漩涡较多使静压分布不均，经导叶的整流作用，次级叶轮径向力变化更为规律。次级叶轮径向合力远小于首级叶轮，说明蜗壳相较导叶对叶轮径向力有更好的改善作用。

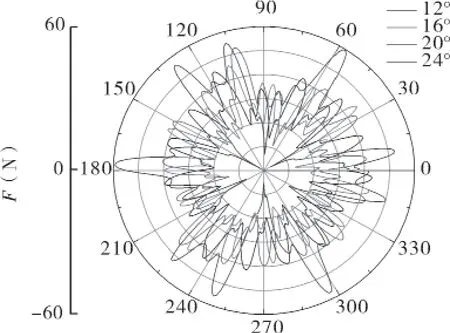
图9 首级叶轮径向合力

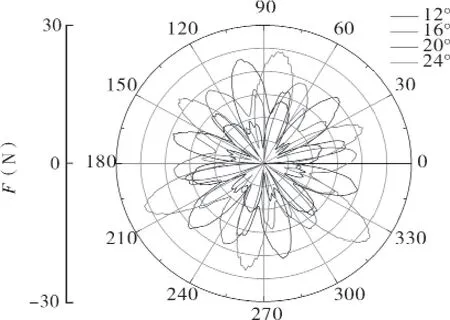
图10次级叶轮径向合力

图11 为叶轮径向力矢量，某一点坐标分别代表某一时刻叶轮径向力的大小和方向。在一个旋转周期内，首级叶轮径向力呈现周期性，即三角星分布。首级叶轮径向力随时间而改变，叶轮旋转一圈，径向力波动五个周期，说明叶轮与导叶的动静干涉作用是径向力变化的主要原因。与此同时，次级叶轮径向力也呈现出一定的周期性，受叶轮与蜗壳隔舌的干涉作用，叶轮旋转一圈，次级叶轮径向力波动两次。随着β2增大，叶轮径向力逐渐增大。

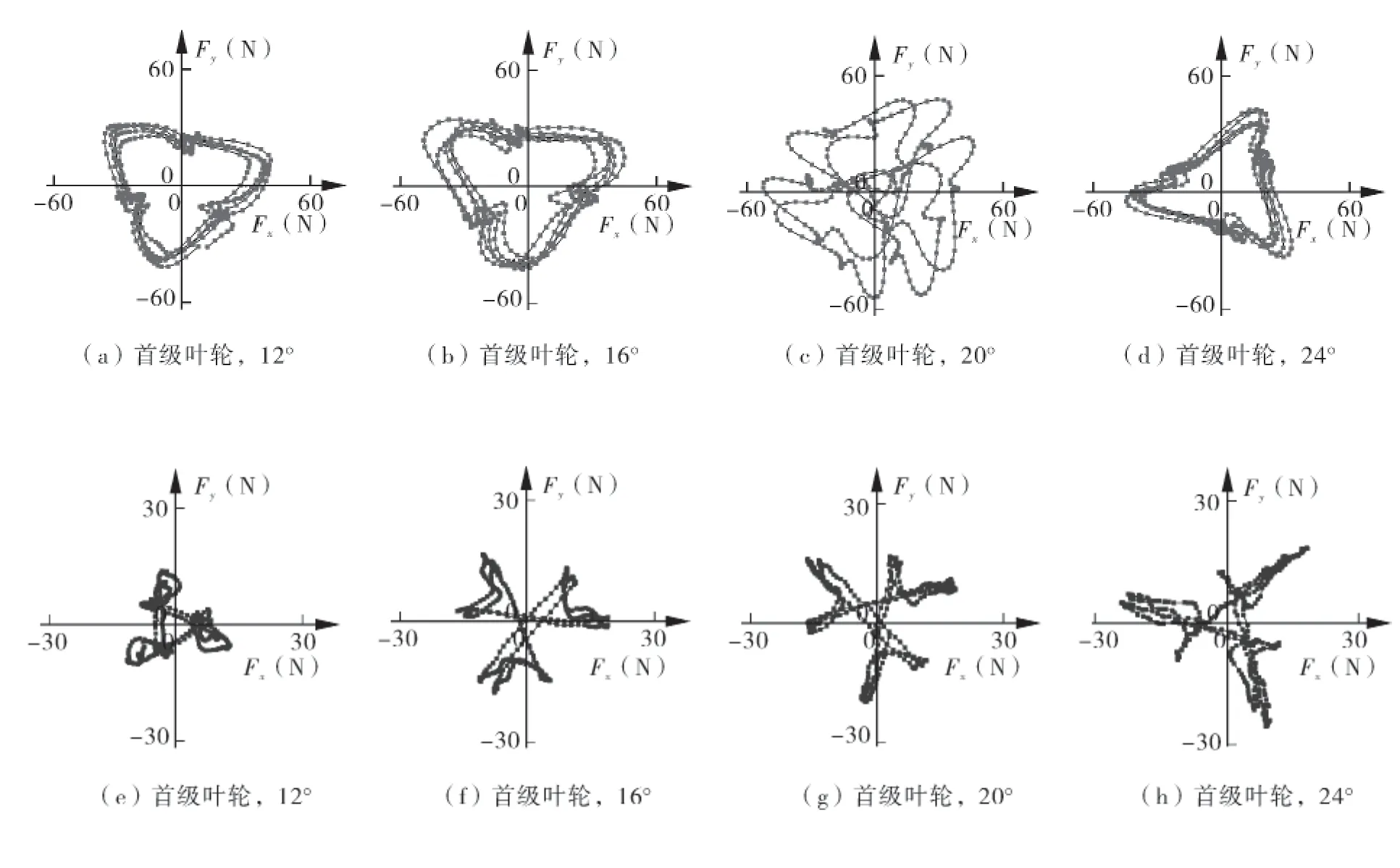
图11 首级、次级叶轮径向力矢量

6 结论

（1）由于叶轮与导叶和蜗壳的动静干涉作用，叶轮出口压力随叶轮旋转呈现周期性变化。当β2为16°和20°时，叶轮出口压力脉动强度明显大于β2为12°和24°；正导叶流道和蜗壳压力脉动强度随β2增大而增大。

（2）随着叶轮旋转，叶轮径向力矢量呈现星型分布，首级、次级叶轮径向力矢量分布大不相同。随着β2增大，叶轮径向力逐渐增大，首级叶轮径向力大于次级叶轮，蜗壳对改善叶轮径向力的作用比导叶更明显。

［1］率志君，张权，陈春来，等.多级离心泵整机流场三维非稳态湍流压力脉动特性分析［J］.哈尔滨工程大学学报，2013，34（3）：306-311.

［2］马新华，冯琦，蒋小平，等.多级离心泵内部非定常压力脉动的数值模拟［J］.排灌机械工程学报，2016，34（1）：26-31.

［3］曹卫东，刘光辉，施卫东，等.多级离心泵内部非定常压力分布特性［J］.农业工程学报，2014，30（14）：64-70.

［4］张德胜，王海宇，施卫东，等.轴流泵多工况压力脉动特性试验［J］.农业机械学报，2014，45（11）：139-145.

［5］蔡建程，潘杰，Guzzom iAnd rew.离心泵隔舌区压力脉动测量与分析［J］.农业机械学报，2015，46（6）：92-96.

［6］RanHongjuan，LuoXianwu.Experim entalstudyofthepressurefluctuationinapum pturbineatlargepartialflowconditions［J］.ChineseJournalofMechanicalEngineering，2012（25）：1205.

［7］张德胜，王海宇，施卫东，等.轴流泵多工况压力脉动特性试验［J］.农业机械学报，2014，45（11）：139-145.

［8］王文杰，袁寿其，裴吉，等.时序效应对导叶式离心泵内部压力脉动影响的数值分析［J］.机械工程学报，2015，51（4）：185-192.

［9］王玉川，谭磊，曹树良，等.离心泵叶轮区瞬态流动及压力脉动特性［J］.机械工程学报，2014，50（10）：163-169.

［10］江伟，朱相源，李国君，等.导叶与隔舌相对位置对离心泵叶轮径向力的影响［J］.农业机械学报，2016，47（2）：28-34.

［11］江伟，李国君，张新盛，等.离心泵蜗壳进口边对叶轮径向力影响的数值模拟［J］.水利学报，2014，45（2）：248-252.

［12］郭豹，刘厚林，谈明高，等.导叶周向安装位置对离心泵叶轮径向力的影响［J］.排灌机械工程学报，2016，34（3）：204-209.

［13］ Zhang M，Tsukamoto H.Unsteady hydrodynamic forces due to rotor-stator interaction on a diff user pump with identical number of vanes on the impeller and diff user［J］.Journal of Fluids Engineering，2005（127）：742-751.

［14］ Akinori Furukawa.Pressure fluctuation in a vaned diffuser downstream from a centrifugal pump impeller［J］.International Journal of Rotating Machinery，2003（9）：285-292.

［15］周林玉.偏离工况下离心泵的压力脉动和振动分析［J］.流体机械，2015，43（2）：52-55.

［16］黄思，张雪娇，宿向辉，等.基于离心泵全流场的流固耦合分析［J］.流体机械，2015，43（11）：38-42.

［17］崔之平，张钊源，杨忠义，等.油田用离心泵汽蚀性能的数值分析与试验［J］.流体机械，2015，43（8）：1-5.

［18］李伟，杨笑瑾，马东华.镍基合金换热管分段式机械胀接试验［J］.压力容器，2015，32（9）：75-79.

［19］杨圆明，扈继承，张玉丰.蒸汽发生器水压试验后干燥技术探讨［J］.压力容器，2015，32（1）：76-80.

［20］周成，刘海滨，诸言会，等.S32168在氯离子环境中的应力腐蚀试验研究［J］.压力容器，2015，32（5）：18-23.

［21］ Guo Lei，Liu Jintao.Pressure fluctuation propagation of a pump turbine at pump mode under low head condition［J］.Science China Technological Sciences，2014（4）：811-818.

Analysis on Pressure Fluctuation and Radial Thrust of Centrifugal Pump under Different Blade Outlet Angle

ZHANG Yi-ning，CAO Wei-dong，YAO Ling-jun，JIANG xin
（Technical and Research Center of Fluid Machinery Engineering，Jiangsu University，Zhenjiang 212013，China）

The effect of blade outlet angle on pressure fluctuation and radial thrust of centrifugal pump are studied based on the experimental results and numerical simulation were in good agreement.A two-stage mine centrifugal pump was chosen for the research object，four kinds of impellers were established with different blade outlet angle.The external performance of centrifugal pump was predicted with CFD simulation，the pressure fluctuation distribution in impeller ，vane and volute as well as radial thrust of impeller were obtained and analyzed comparatively.The results shows that the pressure fluctuation in pump is cyclical，and the higher pressure fluctuation intensity occur when β2are 16° and 20° .The pressure fluctuation in vane and volute are gradually increased with the blade outlet angle increasing，and the intensity in vane is stronger than that in volute，and fluctuation frequency in both vane and volute is blade frequency with different blade outlet angle.The blade outlet angle has certain impact on radial thrust distribution on impellers，the radial thrust of impeller ascend with β2increasing，and the radial thrust of first impeller is larger than the other impeller，volute has greater improvement on impeller radial thrust than vane.

centrifugal pump；numerical simulation；blade outlet angle；pressure fluctuation；radial thrust

TH3；S277.9

A

10.3969/j.issn.1005-0329.2017.11.007

1005-0329（2017）11-0034-07

2016-10-25

2016-12-02

江苏省自然科学基金资助项目（BK20131256）；江苏省重点研发计划竞争项目（BE2017126）

张忆宁（1991-），女，硕士研究生，主要从事流体机械水力优化设计，E-m ail：741609322@qq.com。

曹卫东（1972-），男，副研究员，主要从事流体机械内部流动特性研究，通讯地址：212013江苏镇江市京口区学府路江苏大学，E-m ail：cw d@u js.edu.cn。