贯流风机叶轮参数的模拟研究

舒朝晖，张 强，段亚雄

贯流风机叶轮参数的模拟研究

舒朝晖，张 强，段亚雄

（华中科技大学，湖北武汉 430074）

贯流风机叶轮参数对风机性能有着决定性的影响，基于某企业提供的原型叶轮，通过二维稳态模拟探讨了叶轮前后缘半径Ri与Ro、叶片倾角a以及叶片弯度角γ 等3个重要叶片参数对空调用贯流风机流场和性能的影响。结果表明，叶片前后缘半径比对叶片壁面边界层分离存在较大影响，当Ri/Ro＞1时，通常能够较好地抑制边界层分离，得到较大的出口流量；对于原型叶片而言，其倾角a的最佳取值范围介于25°到30°之间，且随a增大，叶轮入口流场波动减小；弯度角γ越大，叶轮对气流做功越多，γ 为90°时，取得最大流量值716.47m3/h，相比原叶轮，流量提升4.04%。

贯流风机；叶轮参数；流场特性；风机性能

1 前言

贯流风机（crossflowfan）作为空气输送装置被广泛应用于空调领域，尤其是应用于分体壁挂式空调中，其送风性能和噪声特性备受关注。由于其流场极其复杂，目前仍然没有通用的设计理论。

叶轮是贯流风机最关键的送风部件，其结构很大程度上决定了贯流风机的性能。前人对贯流风机叶轮结构做了一系列研究［1～6］。2003年，ALazzaretto总结前人的研究成果，提出并定义了叶轮和外壳的详细形状和位置参数，确定了能够获得较好性能和效率的各参数的取值范围［6］。ALazzaretto提出的叶轮特征参数包括叶轮轴向长度与外径之比L/D2、叶轮内外径之比D1/D2、叶片数Z、叶片入口角b1和出口角b2，主要特征参数的取值范围为 0.7 ≤ D1/D2≤ 0.85；20°≤β2≤45°；70°≤β1≤130°。其后，张师帅等以叶片出入口角、叶片中部厚度、叶片端部厚度、叶片斜扭角度以及叶片圆周分布角等为主要设计参数，实现了贯流风机叶轮几何建模的参数化［7］。另外，很多学者研究了叶片扭曲角、叶片斜度、叶片分布以及叶片边缘形状（如锯齿边）等叶轮参数对贯流风机性能的影响［8～17］。

前人对叶轮横截面参数的研究多集中在叶轮入口角β1和出口角β2上，鲜有学者研究叶片两端厚度对性能的影响。另外，由于气流两次贯穿叶片，气流相对叶片并没有固定的入口角和出口角，所以，从叶片几何设计的角度出发，本文参考Mcnally绘制双圆弧叶片串列叶栅的形位参数，设定了一组叶片特征参数：外径D2、弦长C、前后缘半径Ri与Ro、最大厚度TM、弯度角γ和倾角a。结合某风机厂家提供的空调用贯流风机原型叶轮，本文维持参数D2和C不变，通过二维数值模拟的方法，分别探讨叶片前后缘半径Ri与Ro、弯度角γ和倾角a的改变对贯流风机性能的影响，为生产实践提供参考［18］。

2 贯流风机特征及其物理模型

本文研究的贯流风机位于壁挂式空调室内机的下游，主要由蜗壳、蜗舌以及前弯叶片叶轮构成（如图1）。与轴流风机和离心风机不同的是，贯流风机气流由径向进入，两次贯穿叶片后从出口流出，其流场最典型的特点是，叶轮尾缘会产生大量的脱落涡，这些涡不断破碎、扩散和组合，最终在蜗舌附近（图1中虚线方框）形成一个较稳定的偏心涡，其位置、大小和强度决定着贯流风机的流场特性。

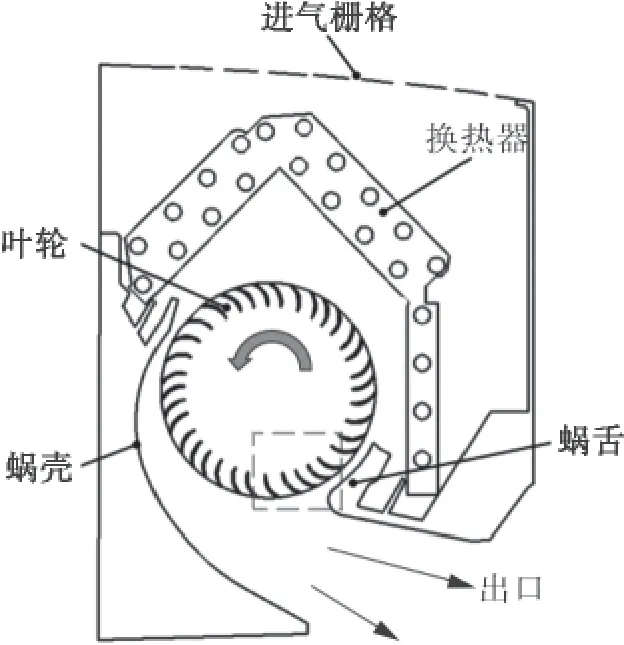
图1 空调室内机结构示意

叶片横截面型线和各参数如图2所示，图（a）为由叶片角β1、β2和内外径定义的等厚叶片（T为厚度），其中角β1与β2的顶点分别为叶片中弧线与叶轮内外圆的交点。图（b）为由本文设定的特征参数确定的叶片。

图2 叶片横截面示意

本文的物理模型由企业提供的原型机简化而来，如图1所示，叶片型线与图2（b）相同。蜗舌间隙4.6mm，蜗壳间隙3.7mm，叶片不等距分布，叶轮主要特征参数列于表1中。

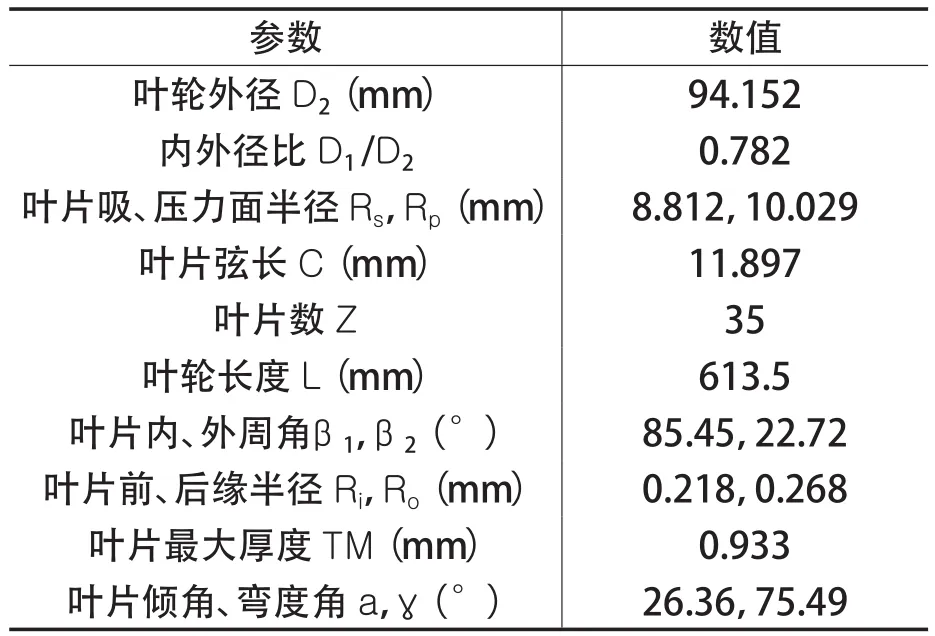
表1 企业提供的贯流风机叶轮主要特征参数

叶轮转速为1205r/m in，叶轮外缘速度为5.94m/s，马赫数Ma＜0.02，以叶片弦长为特征长度的雷诺数Re=4838，可视为不可压湍流模型。且叶片都为直叶片，贯流风机流场具有良好的轴向一致性。综上，实际模型可简化为二维不可压湍流模型。

3 数值模型

3.1 网格划分

计算网格如图3所示，计算域为半径为10D2的半圆区域，外围圆环区域（图中标记A，B）采用结构网格，其它区域采用非结构网格（叶轮区域D为三角形网格），并对叶轮、蜗舌和蜗壳附近进行加密处理。在进行网格无关性验证后，最终选取的全局网格数约为19.5万（改变叶片参数后叶轮区域网格会微小变化），其中叶轮区域D约10万，外围结构网格数为15520，换热器区域C为7920，叶轮壁面边界层为15层。转子圆环宽度d以及圆环内外圆与邻近叶尖的间歇对流场模拟结果影响较大，未见对其大小设置作严格规定的相关理论。本文中，如无特殊说明，则区域D的内外径保持不变，分别为71.582mm和96.152mm，即分别与企业提供的原型叶轮内外叶尖间隔1mm。

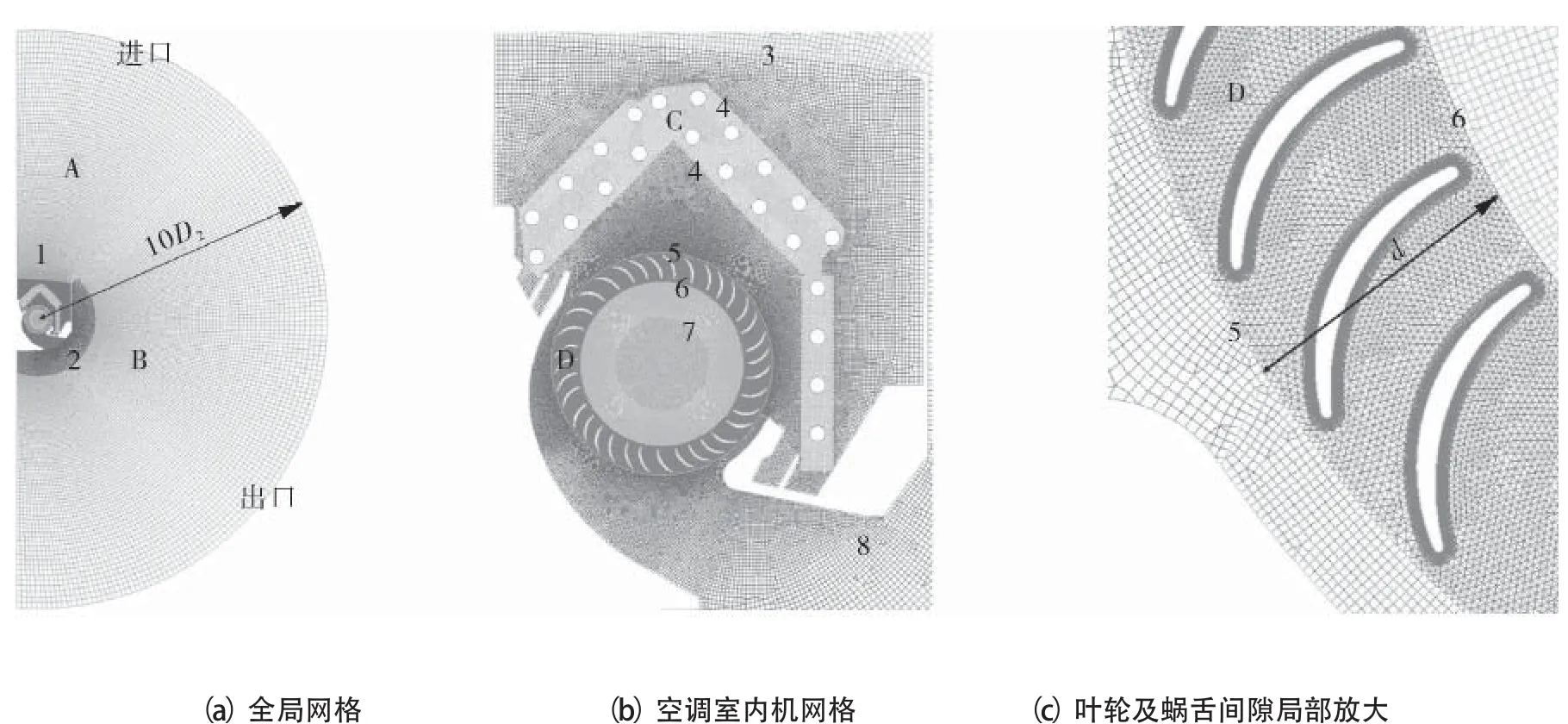
图3 网格示意

3.2 模拟条件设置

边界条件设置：室内机外围进出口（图3（a））分别设置为压力进出口，表压均为0Pa；图3中交界边1，2，5和6设置为Interface边界；交界边3，4，7，8以及蜗舌加密区的两端边线设置为Interior边界；其它边界均设置为壁面Wall；换热器区域C设为多孔介质区域；叶轮区域D采用多坐标参考系MRF，即设置为Fram eMotion；叶片壁面设置为旋转壁面。

其它条件设置：空气密度根据通风机标准进气状态设定为1.2kg/m3，选取RNGk-e湍流模型，壁面采用Scalab leWall模型，压力速度耦合采用SIMPLEC格式。压力采用标准差分格式，其它空间离散设置为二阶迎风格式。

4 模拟结果及分析

4.1 前、后缘半径的影响

原叶轮前、后缘半径分别为Ri=0.218mm、Ro=0.268mm，为了探究前、后缘半径的影响，保持其它叶片横截面特征参数不变，分别改变Ri，Ro（D1会随其微小变化，具体值将列出）进行二维稳态计算，不同条件的性能参数变化情况见图4。

图4 不同前、后缘半径情况的性能参数变化

叶轮功率：

式中P——叶轮功率，W

T——单位长度的叶轮转矩，N·m

ω——叶轮旋转角速度，rad/s

全压效率：

式中Pe——风机有效功率，Pe=ΔPeQ

ΔPe——风机全压，Pa

Q——出口风量（注意轴向长度），m3/h

各序号对应的前后缘半径值如表2所示（为方便表述，令常数a=0.218mm，a～1.23a表示0.218～0.268mm），其中序号4对应原叶片，同时 附上对应的叶片角β1，β2以供参照。

表2 不同前后缘半径的流量变化和对应的叶片角

由图4和表2可得，固定Ri=a时，当Ro从2.1a（此时后缘直径已十分接近于叶片最大厚度TM）逐渐减小到a时（序号1到5），风机出口流量、叶轮功率和全压效率均小幅增大，说明这一过程中叶轮对气流做功增多且流动损失相对减小；固定Ro=a时，当Ri从a逐渐增大到2.1a时（序号5到9），风机流量逐渐减小，但变化程度十分微小，叶轮功率基本不变，全压效率呈微小的减小趋势，说明流量的微小变化主要由流动损失的增大所致。

总体而言，随叶片前后缘半径变化，3个性能参数均先微小增大（序号1到5）后基本不变（序号5到9），都在序号5处取得最大值。流量最大值相对于流量极低值（序号1）增大2.42%，相对于原风机（序号4）增大0.58%。

图5，6依次给出了a～1.8a，a～a和2.1a～a 3种叶片入口和出口局部涡量云图。

图5 叶片入口局部涡量云图

图6 叶片出口局部涡量云图

由图可知，随叶片前缘半径增大（Ri/Ro增大），入口叶片吸力面上的涡量更加贴近壁面，吸力面附近尾涡区稍有减小（参见图中椭圆标记），这是因为，根据翼型理论，叶片入口端大出口端小（圆头尖尾）能够有效减小壁面逆压梯度，从而抑制边界层的分离或使分离点后移，使得尾涡减小，流动阻力与损失减小；而出口叶片上的涡量分布则刚好与入口情况相反，只是没有入口明显，仔细观察出口叶片尾缘（图中圆形标记），可以发现，随前缘半径增大，叶片尾缘附近的涡量范围略有增大且尾缘附近涡量强度很大。即随叶片前缘半径增大（或后缘半径减小），贯流风机叶轮进口流道的流阻减小而出口流道的流阻增大。因此，理论上存在一组最佳的前后缘半径值，使得整个叶轮流道的流阻最小，从而使得风机流量最大。由以上9组模拟结果可知，当Ri≥Ro时，一般都能获得较大的出口风量，且此时全压效率和叶轮功率基本不变。

综上可知，叶片前、后缘半径Ri，Ro对贯流风机性能的影响较小。一般而言，可使用Ri略小于Ro的叶片来适当降低叶轮功率，而为获得较大的流量值和全压效率最好使得Ri≥Ro。

4.2 叶片倾角α的影响

由于叶片倾角改变时，叶轮内径发生较大变化，为保证转子区域D的网格质量，本节把区域D（图3）的内径由71.582mm改为70mm。不同叶片倾角时贯流风机性能参数变化情况如图7所示，虚线对应原叶片。不同情况的具体流量值和叶片角示于表3中。

图7 不同倾角α时的性能曲线

表3 不同叶片倾角的流量变化和对应的叶片角

需要特别说明的是，当倾角为15°、20°和23°时，风机出口流量模拟值存在比较明显的波动，流量值无法收敛，推测这3种情况下风机内流场十分紊乱。为便于对照，本文选取从8000步到10000步的模拟结果的流量平均值作为这3种情况对应的参考流量。下文将对倾角为20°的流场予以分析。另外，对于叶片弯度角为45°和60°的情况，本文也采取了相同的处理方式，后文将不再说明。

由图7和表3可知，倾角α由25°增大到30°的过程中，风机各性能参数的变化都十分微小（几乎不变）。当α由30°变为35°时，各性能参数均明显减小。

图8给出了不同倾角时贯流风机内部的静压云图和流线分布。

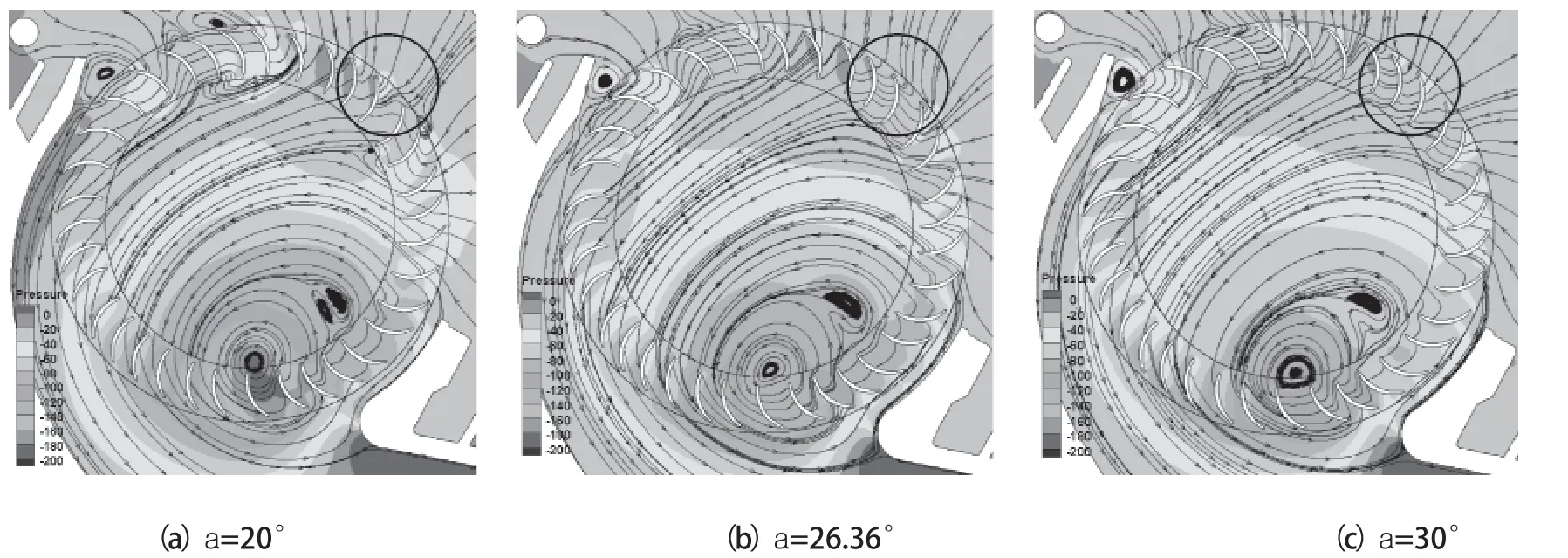
图8 不同倾角静压云图和流线分布

结合图7和图8可知，随倾角α增大，偏心涡位置越靠近蜗舌，这是因为倾角越大，涡核下游附近气流以更大的负攻角通过叶片流道，下游叶片压力面产生的脱落涡更多，对偏心涡的诱导作用更大。而一般涡心越靠近蜗舌，出口回流区域越小，风机流量趋于增大；偏心涡位置向蜗舌移动使得入口气流方向发生明显改变，气流在入口叶片吸力面产生的脱落涡减少，因而入口流场紊乱程度明显减小，流动损失减少，风量和效率趋于增大。另外，涡核压力随倾角增大而变大，这导致涡核对流场的诱导作用减小，从而使风机整体流量趋于减小。总的来说，可以推测，倾角为15°、20°和23°时，叶轮入口流场的紊乱性对整个风机流场产生了强烈扰动，使得出口流量无法收敛；倾角由25°增大到35°的过程，一方面由于偏心涡靠近蜗舌使得风机流量趋于增大，另一方面由于涡心压力变大导致流量趋于减小，当前者趋势大于后者时，风机流量增大，反之就减小。同时，由于倾角越大，风机叶轮入口流场波动越小，所以在流量变化不大时，可以选择较大的叶片倾角。

4.3 叶片弯度角γ

图9给出了不同叶片弯度角时贯流风机各性能参数的变化情况，虚线对应原叶片，不同情况的具体流量值和叶片角示于表4中。

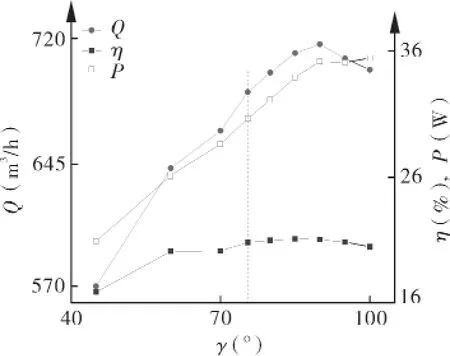
图9 不同弯度角γ时的性能曲线

由图9和表4知，出口流量随弯度角γ 增大先增大后减小，当γ＞75.49°后出口流量增大趋势明显减小，当γ=90°时取得流量最大值716.47m3/h，相对原叶轮（γ=75.49°），风机流量提升4.04%；叶轮功率随γ 增大近于线性增大，当γ＞90°后增大幅度减小，γ=90°时的叶轮功率相比原叶轮功率增大14.87%；全压效率随γ 增大先逐渐增大，当γ＞75.49°后基本不变，当γ＞90°后，开始减小；γ=90°时的全压效率与原叶轮基本相同。这说明，随弯度角增大流量的增大主要得益于叶轮对气流做功增多；当γ＞75.49°后流量的增量远小于叶轮功率的增量且全压效率基本不变，说明这一过程流动损失并没有明显变化，叶轮对气流做功主要使得出口气流的全压大幅提升而对气体输送量的提升并不十分明显。

图10不同弯度角速度云图和流线分布

图10 给出了弯度角为45°、90°、100°3种情况的流线图和速度云图。由图可知，叶轮内的低速区主要出现在偏心涡区域和叶轮入口部分湍动严重的叶片尖端。随γ增大，叶轮入口低速区域和旋涡区域明显减小，结合流线图可以看出这主要得益于叶轮入口尾涡减小；并且叶轮出口高速区域明显增大，说明弯度角的增大提升了叶轮对气流的做功能力，这与图9中性能曲线的变化情况相符合。另外，结合流线图和速度云图可以明显看出，弯度角的改变使偏心涡涡心位置发生了变化，一方面，随弯度角增大，涡心位置逐渐向右移动，越来越靠近蜗舌，出口回流区域明显减小；另一方面，弯度角越大，涡心位置越靠近叶轮轴心，偏心涡上游循环区域明显增大。因此，存在一个最佳的叶片弯度角γ，使循环区域尽可能小，从而使得风机出口流量尽可能大。由模拟结果可知，在不考虑风机效率的情况下，这一最佳弯度角应在90°附近取得。涡心位置的改变以及入口尾涡减小的原因与“4.2叶片倾角α的影响”中的分析相同。

5 结论

（1）叶片前后缘半径Ri与Ro、弯度角γ和倾角α等叶片参数对贯流风机流场有着重要影响，它们与叶片表面边界层的分离息息相关，一定程度上决定了偏心涡的位置、大小和强度。

（2）叶片前后缘半径比Ri/Ro主要影响着叶片壁面的边界层分离以及叶轮尾涡区域的大小，一般而言，Ri/Ro值越大，叶轮总体尾涡区域越小，流动损失越小。

（3）叶片倾角α 越大，偏心涡越靠近蜗舌，出口回流区域越小，但涡心压力越来越大，不利于涡核对气流的吸引诱导。对于原型叶轮，当α≤23°时，叶轮入口涡脱落掺混十分严重，贯流风机流场无法稳定，出口流量不能收敛；当α＞30°时，风机流量和全压效率均明显下降；对企业提供的贯流风机而言，最佳叶片倾角范围为25°≤α≤30°。

（4）叶片弯度角γ越大，叶轮对气流做功越多。当γ＞75.49°后，叶轮对气流做功主要使得出口气流的全压大幅提升而对气体输送量的提升并不明显。就本文而言，若考虑风机的综合性能，最佳弯度角应在75.49°附近取得；若只是为了获得较大的出口流量，则弯度角γ可取为90°，此时取得最大流量值 716.47m3/h。

［1］埃克B，著.沈阳鼓风机研究所，译.通风机（第一版）［M］.北京：机械工业出版社，1983.

［2］Yam afu jiK.Studiesontheflowo fcross-flowim pe-llers（1streport，analyticalstudy）［J］.Bu lletino ftheJSME，1975，18（123）：1018-1025.

［3］Yam afu jiK.Studiesontheflowo fcross-flowim pe-llers（2ndreport，analyticalstudy）［J］.Bu lletino ftheJSME，1975，18（126）：1425-1431.

［4］ Lazzaretto A，Toffolo A，Martegan，A D. A systematic experimental approach to cross-flow fan design［J］. Journal of Fluids Engineering，2003，125：684-693.

［5］ Lazzarotto L，Lazzaretto A，Martegani A D，et al. On cross-flow fan similarity：effects of casing shape ［J］. Journal of Fluids Engineering，2001，123：523-531.

［6］ Lazzaretto A. A criterion to define cross-flow fan design parameters［J］. Journal of Fluids Engineering，2003，125（4）：680-683.

［7］张师帅，罗亮.空调用贯流风机叶轮几何建模的参数化［J］.风机技术，2006（5）：14-16.

［8］刘敏，王嘉冰，吴克启.数值模拟不等距叶片对贯流风机的影响［J］.工程热物理学报，2007，28（2）：211-214.

［9］田杰，欧阳华，李游,等.基于交错叶轮技术的横流风机气动声学特性研究［J］.机械工程学报，2010，46（3）：97-102.

［10］朱宗铭，邬烈锋，谭华兵，等.贯流风机性能参数实验与扭曲角优化［J］.机械设计与制造，2012（1）：203-205.

［11］王银姣，卢剑伟，江斌，等.利用CFD技术研究叶片斜度对贯流风机性能的影响［J］.合肥工业大学学报：自然科学版，2012，35（7）：882-887.

［12］ Yamakawa H. Development of high efficiency and low noise cross-flow fans for room air conditioner indoor unit［C］.ASME 2014 4th Joint US-European Fluids Engineering Division Summer Meeting collocated with the ASME 2014 12th International Conference on Nanochannels，Microchannels，and Minichannels. American Society of Mechanical Engineers，2014：V01BT10A024.

［13］陈阳，黄友根，王军，等.倾斜蜗舌对前弯离心风机蜗舌区域流动影响的数值研究［J］.流体机械，2015，43（9）：26-30.

［14］丁学亮，叶学民，李春曦.轴流风机叶片展向结构变化对性能影响的数值分析［J］.流体机械，2015,43（9）：43-49.

［15］贾志彬，陈强，汪军，等.微穿孔消声器在小型高速离心风机中的应用研究［J］.流体机械，2015,43（8）：6-10.

［16］池优阳，阮竞兰.粮油机械产品的低碳设计制造［J］.包装与食品机械，2015,33（5）：55-58.

［17］巩桂芬，陈宁.螺旋横向运动式去皮裹包果蔬产品的机械及力学研究［J］.包装与食品机械，2016,34（5）：33-37.

［18］ Crouse J E，Nally W D M. Fortran program for computing coordinates of circular arc single and tan -dem turbomachinery blade sections on a plane［Z］. 1970.

Numerical Investigations on the Impeller Parameters of the Cross Flow Fan

SHU Zhao-hui，ZHANG Qiang，DUAN Ya-xiong
（Huazhong University of Science and Technology，Wuhan 430074，China）

Impeller parameters have great effect on the performance of the cross flow fan. Based on the blade provided by a company，the influences of several important blade parameters such as leading radiu（Ri），rear radiu（Ro），blade tilt angle（a） and camber angle（γ） on the flow field and performance of the cross flow fan，has been studied by two-dimensional steady simulation.The results show that，the ratio of Riand Ro has great effect on boundary-layer separation of the blade surface，the boundary layer separation is inhibited and higher outlet flow rate is obtained when Ri/ Ro＞1. Blade tilt angle a of the prototype blade can be chosen in the ranges 25°≤a≤30°，and in which range，the fluctuation of the impeller inlet flow decreases with a increases. The greater the camber angle γ，the more the impeller works on the airflow. Moreover，when γ is equal to 90°，the flow rate achieves the maximum of 716.47 m3/h，enhanced 4.04% compared to the original impeller.

cross flow fan；impeller parameters；flow field characteristics；fan performance

TH43

A

10.3969/j.issn.1005-0329.2017.11.005

1005-0329（2017）11-0022-07

2016-11-24

2017-04-19

广东省科技计划项目（2013B090600061）

舒朝晖（1970-），男，博士，副教授，主要从事制冷空调及其节能技术、高效热交换设备与技术等方面的研究,通讯地址：430074湖北武汉市华中科技大学能源与动力工程学院化工装备与技术研究所，E-m ail：shuzhaohui@hust.edu.cn。