基于PSO-BP的调控型气体密封状态参数智能计算方法研究

王 磊，李双喜，朱乔峰，李 欢

基于PSO-BP的调控型气体密封状态参数智能计算方法研究

王 磊，李双喜，朱乔峰，李 欢

（北京化工大学流体密封实验室，北京 100029）

调控型气体密封作为一种非接触密封，可以提高系统服役过程中运行的稳定性，但是目前密封状态参数的计算方法存在计算模型建立过程繁杂以及迭代计算耗时较长等缺点。本文采用了一种符合智能调控系统输出精度及时效性要求的粒子群算法（PSO）优化下的BP（BackPropagation）神经网络方法，开发了基于PSO-BP的调控型气体密封状态参数的智能调控程序。并且对神经网络模型初始阀值与权值进行取值优化，讨论了粒子群种群数量，隐含层数，神经元数等参数对智能计算程序的影响。搭建了基于PSO-BP的调控型气体密封试验验证系统，验证了密封状态参数智能计算程序的精确度。实现了调控型气体密封的智能调控，提高了调控型气体密封抗干扰能力，促进了大型离心压缩机向宽工况、高参数、高效率和智能化方向发展。

调控型气体密封；神经网络；智能调控；性能参数

1 前言

典型的调控型气体密封结构（RGS）如图1所示［1］，动环随轴旋转，静环浮装于静环座。圆周贯通的均压槽加工在密封端面，并与调控气引入通道末端的节流装置（本文采用小孔节流）相连通。外部的调控气（压力为ps）通过节流装置导入到密封间隙内（压力降为pd），借助静压效应产生一定开启力，密封运转时动压槽的动压效应进一步增大开启效果，使静环端面获得稳定的工作气膜。

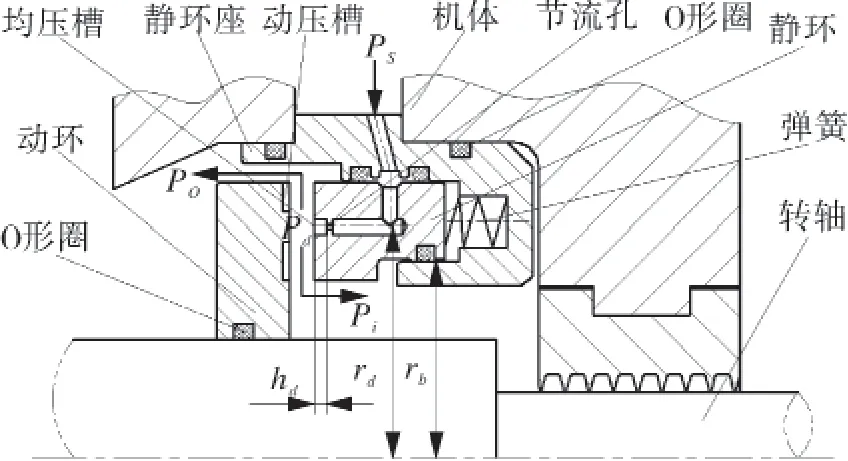
图1 RGS工作原理示意

在密封的任何状态都可以通过调节调控气压的大小而调节或设定密封的工作状态，故这种密封称为调控型气体密封。当密封状态（如密封内外径处的压力、转速等）变化时，可以改变调控气压力大小，进而改变密封的工作状态，防止密封碰撞或泄漏过大而失效。

调控型气体密封辅以智能调控系统，在密封运行过程中采取相应的响应动作，可以扩大此种密封工作适用范围，提高运行稳定性。得益于智能调控系统［2］，使得该种密封具备抗干扰、可调控及智能化的特点，有着广泛的运用前景［3，4］。

调控时，需要实时确定密封的状态参数，以往针对调控型气体密封的研究中，已经有大量的文献表明，商业软件（如FLUENT、CFD等）能够很好地完成密封状态参数计算［5］，但该类方法仅能针对具体尺寸单独建模分析，其结果精度较高［6，7］，但时间较长。为便于研究不同结构的密封性能，不少学者采用 MATLAB 编写了计算程序［8，9］，实现参数化分析，极大地提高了分析效率，但计算时间仍在20～50m in，无法满足调控时效性要求。因此需要一种符合智能调控系统输出精度及时效性要求的密封参数计算方法。

针对这一问题，本文基于调控型气体密封特点，建立了BP（BackPropagation）神经网络计算模型［10，11］，并采用粒子群算法针对神经网络模型初始阀值与权值进行取值优化［12］，研究了粒子群算法（英文缩写为PSO）优化的BP神经网络实时分析密封运行状态，分析不同算法结构下模型精度。

2 密封状态参数的智能计算程序

2.1 PSO-BP的工作原理

为满足调控过程中的时效性要求，为执行机构提供精确的控制信号，本文提出了一种基于BP神经网络的状态参数智能计算方法。该方法不仅能够适应调控型气体密封各参数高度非线性的特点，还具备较高的时效性。为避免网络出现过度学习及陷入局部最优的困境，引入粒子群优化（PSO）算法为其提供全局优选的初始权值和阀值。优化后的算法具备规模小、速度快及鲁棒性强等优点。

调控型气体密封控制过程中，输入信号有：期望膜厚hw（或期望泄漏率qiw）、压缩机出口压力po及转轴转速n，因此神经网络中输入层具有3个神经元分别接受被控目标量及被控对象输出量，输入层单元采用线性函数；隐含层共有m层，各层含有pm个S型单元；输出层采用2个线性单元，输出调控气压力ps与期望泄漏率qiw（或期望膜厚hw）。最终建立的网络结构如图2所示。

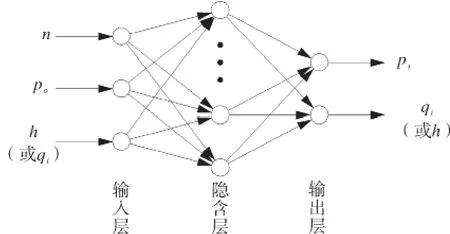
图2 调控型气体密封状态参数智能计算网络结构示意

2.2 密封状态参数的智能计算过程

针对调控型气体密封的参数智能计算方法，其具体运算步骤及关键计算如下：

（1）对系统程序进行初始化，并在［-1,1］范围内给每个权值随机赋值，同时输入计算允许误差εo和最大进化次数K。

（2）对调控型气体密封学习样本进行归一化处理。

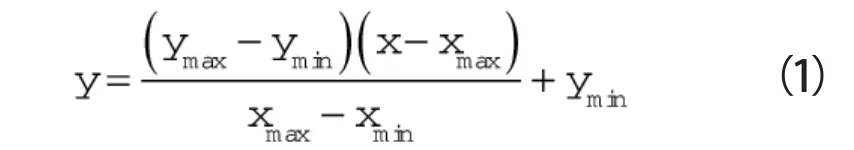
式中ymax，ymin——映射函数参数，分别取 -1，1

xmax，xmin——调控型气体密封同类参数原始数据库中最大值、最小值

（3）PSO初始化粒子群，输入基本参数：粒子位置范围［-5，5］、速度范围［-1，1］；种群数量S；在限制范围内赋予每个粒子随机位置Lj及速度Vj。

（4）通过BP网络计算每个粒子对应的网络真实输出Yo，计算每个粒子所处位置所取得的输出精度，即适应度值。

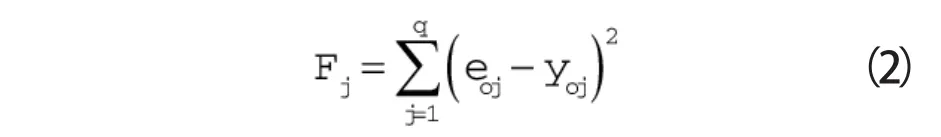
令其为个体最优值Fjb及Ljb的初始值，选取群体中最小适应度值为群体最优适应度值Fs及Ls的初始值。

（5）对粒子速度及位置进行更新寻优：

式中j ——下标，j=1,2,3,…,n

d ——下标，d=1,2,3，…，D

ω——惯性权重，ω=1

c1，c2——加速度因子，c1=c2=1.495

r1，r2——分布与［0，1］间的随机数

（6）计算更新后的粒子适应度函数值Fj并进行最优值遴选与替换，比较适应度值或搜索次数是否达到要求：若达到停止条件继续步骤（7），否则为进入步骤（5）。

（7）将全局最优位置 Ls=（ls1,ls2,ls3，···，lsD）T作为BP神经网络初始权值阀值。

（8）计算各层神经元输出。

式中j ——第j层神经元

f——该层响应函数

n——该层神经元含有节点数

若为中间神经元时，该层输出即为下一层输入：xj+1i=yji。当该层为输出层时，yji为反馈输出参数yoi。

（9）根据梯度下降法计算网络层间反馈参数δωj。

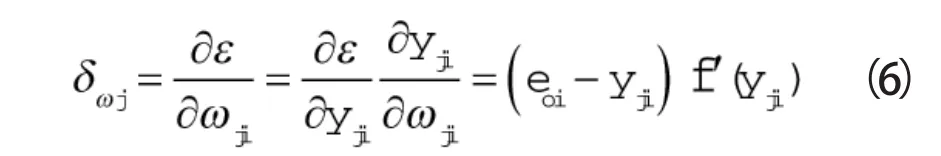
（10）进行权值修正。

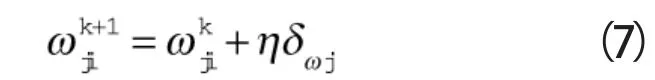
式中k ——当前进化次数

η ——学习速率

（11）根据网络输出Yo与期望输出Eo计算网络输出误差ε。

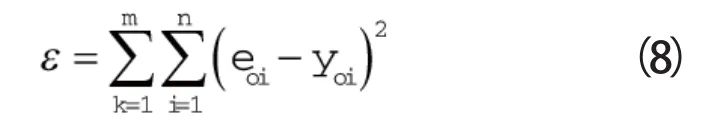
（12）判断是否达到停止条件，若不符合要求则进入步骤（8），若符合要求则完成网络训练。此后即可读取预处理后的输入参数，及时输出密封调控参数。

完成关键计算后，形成基于PSO-BP的调控型气体密封参数智能计算程序，其流程如图3所示。

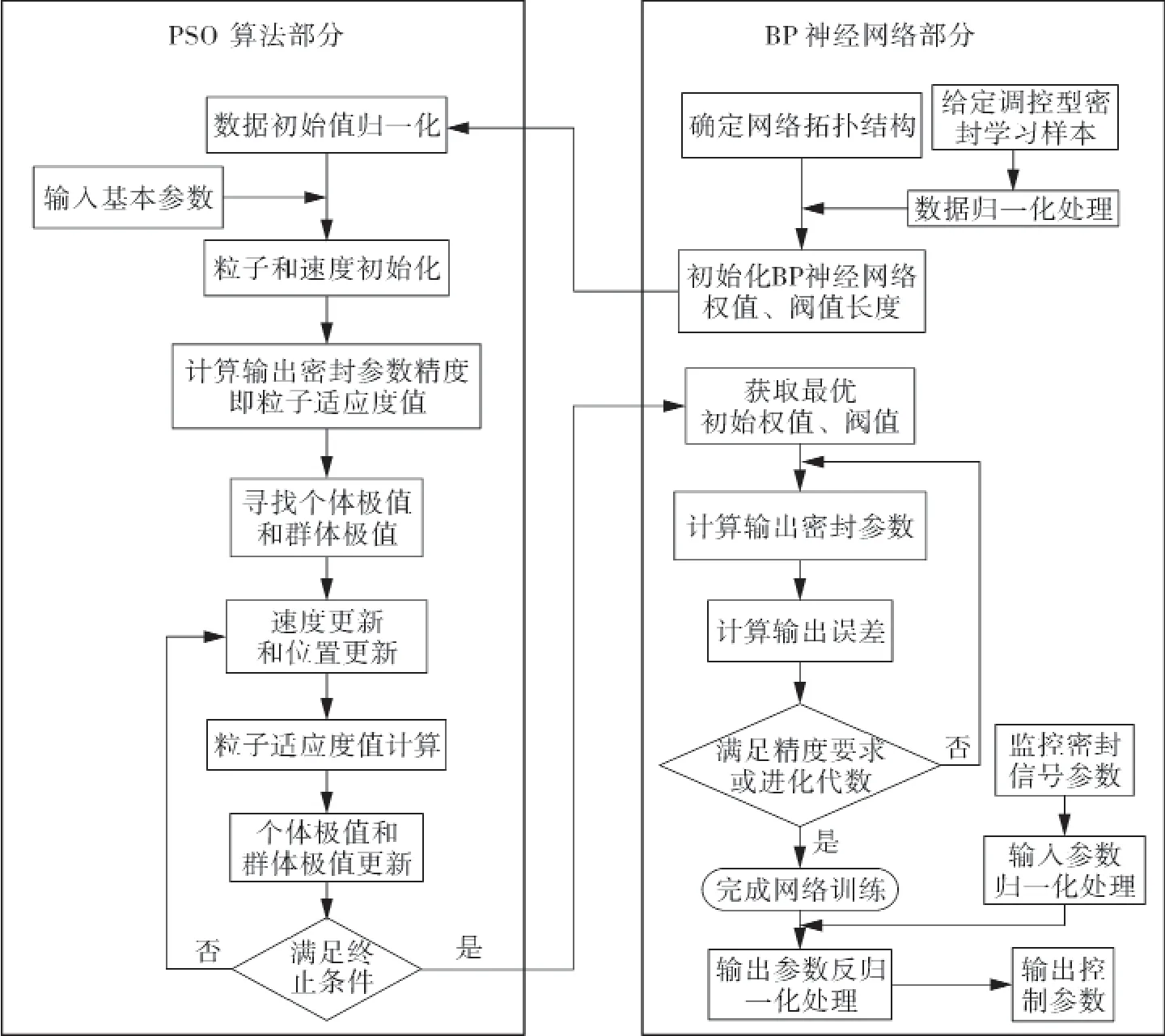
图3 调控型气体密封状态参数智能计算

3 密封状态参数的智能计算程序的学习和训练

针对不同的调控目标，智能计算程序的输入参数与输出参数有所不同，具体设定见表1。为提高程序普遍适用性及数值关联性，定义以下2组控制参数。（1）密封调控比：调控气压力ps按比例转换：

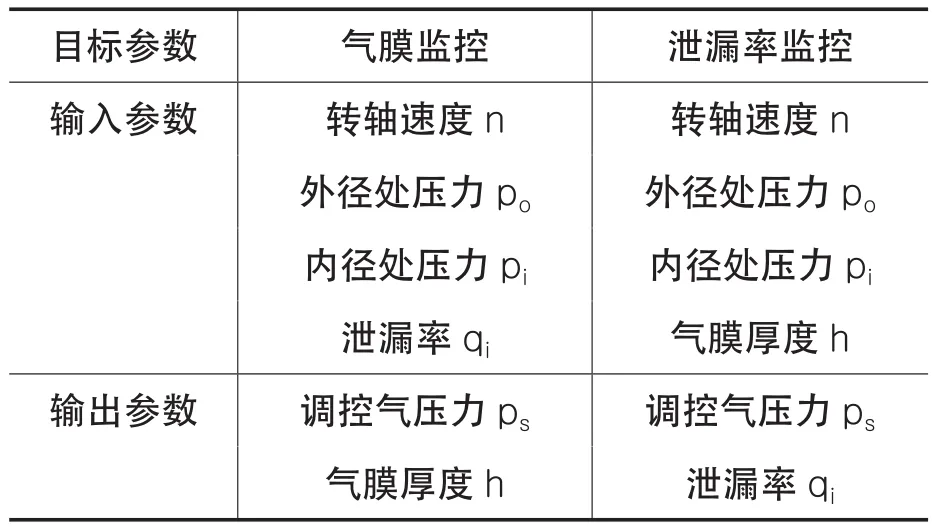
表1 不同目标参数监控参数分

（2）密封压力比：密封介质压力po转换：

为让学习样本在全面有效的基础上尽量减少学习样本数量，样本针对压缩机开、停车过程中可能出现的各种状态，其根据调控比Λ、密封介质压力po和转轴速度n3个实际变量划分数据分布。其取值见表2。

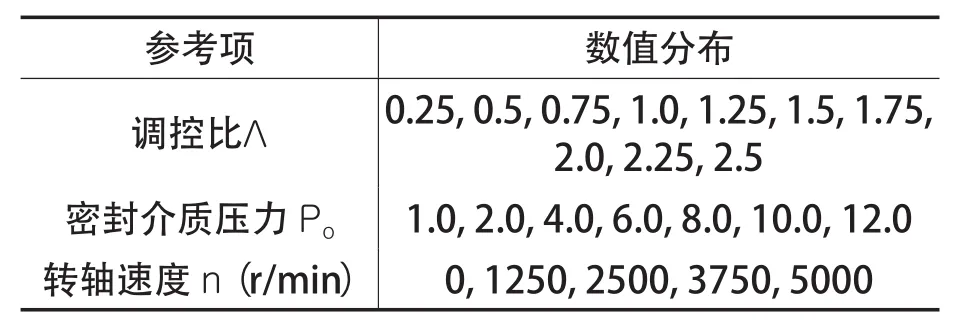
表2 学习样本变量取值

根据表2变量取值，进而取得其唯一对应的气膜厚度h及泄漏率qi参数。将以上一一对应的调控比Λ、密封介质压力po、转轴速度n、气膜厚度h及泄漏率qi作为学习样本，最终选取了学习样本共350组。

3.1 智能计算程序关键参数的设定、优化

针对种群数量S、隐含层节点数nH及隐含层层数J进行优化，择优中以网络训练精度和训练时间为参考量。

（1）种群数量S

在隐含层数J=1，隐含层节点数nH=6时，网络精度及训练时间随种群数量S的变化如图4所示。随着S增大，程序精度ε先快速减小，然后变化趋于平稳；而训练时间t随着种群数量S增加基本呈线性递增。因为算法求解迭代次数随着种群数量增加而线性增加，因此计算时间与基本S呈正比例关系；但S较小时，各粒子群中个体靠近最优位置的概率及数量大大降低，然而当种群数量S增加时，粒子靠近最优位置的概率先快速增加，但达到一定数量时，粒子由于具有c1加速度因子控制的社会习性，搜索最优位置的效率便趋于稳定，即精度趋于平稳。因此由图4（a）可取得较优的种群数量S=30。

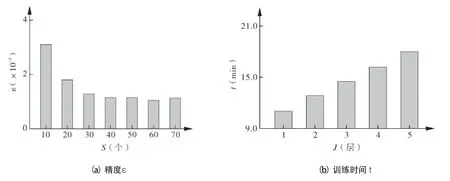
图4 种群数量S对密封程序性能的影响（J=1,nH=6）

（2）隐含层节点数nH

节点数太少，网络不能很好的学习，需要训练的次数及样本数量增加，且精度也受影响；但节点数太多，训练时间将大大增加，网络容易过拟合；一般问题神经网络的误差具有随着隐含层节点数增加呈现先减小后增加的趋势。

在隐含层数J=1，种群数量S=30时，网络精度及训练时间随隐含层节点数nH的变化如图5所示。从图中可以看出，精度ε随隐含层节点数nH先提高再降低，因而可选择隐含层节点数为nH=10。

图5隐含层节点数nH对网络性能的影响（J=1,S=30）

（3）隐含层层数J

在种群数量S=30，隐含层节点数nH=8时，网络精度及训练时间随种群数量S的变化如图6所示。从图中可以看出，随之隐含层层数J增大，程序精度ε略微减小，但总体变化不大；而训练时间t随着隐含层层数J增加基本呈线性递增。因为算法求解迭代次数随着隐含层层数J增加而线性增加，因此计算时间与基本S呈正比例关系；但网络结构在一定神经元节点数时已经具有较好的计算精度，因此隐含层层数的增加对预测精度提高并不明显故图6（b）可取得较优的隐含层层数J=1。

图6隐含层层数J对网络性能的影响（nH=8,S=30）

根据以上分析可确定状态参数智能计算程序结构见表3，并利用此程序结构进行最终学习训练，对调控型气体密封进行参数计算。

表3 密封状态参数智能计算程序结构

隐含层节点数nH（个） 10隐含层层数J（层） 1

3.2 调控型气体密封状态参数智能的计算精度

参数计算可分为以气膜厚度或泄漏率为目标参数进行检验，本文选取泄漏率作为检验参数，对比计算值与非学习样本的实际工况数据组，完成智能计算程序实际工况检验。

其计算检验结果如图7所示。可以看出程序能够对实际工作状态进行精确控制参数输出。以泄漏率为目标时，第2组调控气压力输出误差仅为1.13%，泄漏率输出误差为1.31%。除第2组样本外，其他组输出误差都控制在1.00%以下，达到了实际工程要求。通过对学习后的密封状态参数智能计算程序进行实际工况参数检验，程序具有很好的参数计算精度。

图7 以泄漏率为目标的实际工况参数计算结果

3.3 调控型气体密封状态参数智能的计算速度在调控型气体密封的调控中，指导信号的时效性同样值得关注。将训练好的智能计算程序与依靠纯流体机理数值计算方法迭代求解进行对比［13，14］，计算所需时间如表 4 所示。

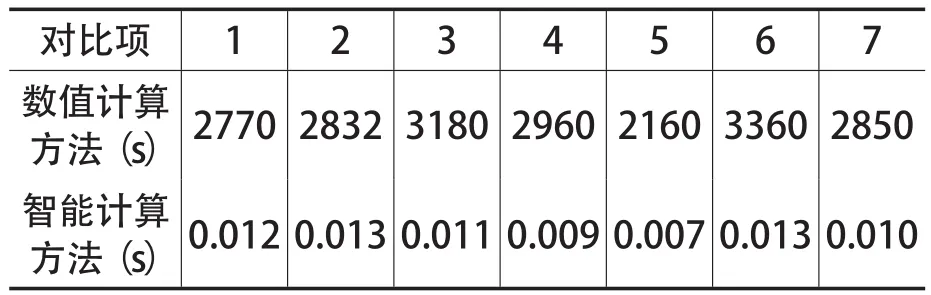
表4 不同方法计算所用时间

从以上计算时间对比结果可以看出，采用智能计算方法所用的计算时间均在0.013s以下，该值远小于数值计算方法所需时间。由此可以看出虽然智能计算程序需要一定时间进行逻辑训练，但是完成训练的程序计算速度能够迅速地输出指导信号；并且完成训练的程序，其后续学习与计算输出能够同时进行，并不会增大控制信号输出计算所需时间。

4 计算程序的试验验证

4.1 试验系统

图8所示为密封状态调控系统流程。在密封智能调控系统工作时，离心压缩机转速n或出口压力po发生变化，调控型气体密封气膜厚度和泄漏率随之发生变化，通过光电转速传感器和电涡流位移传感器等设备将物理信号转化为与之成比例变化的电压信号，经过信号调理、A/D转换后进入计算机，将采集目标量与期望值比较，并经过密封参数计算程序输出控制信号，通过D/A转换控制电磁阀开关，进而调节平衡罐内压力ps，最终实现调控型气体密封膜厚（或泄漏率）的控制。

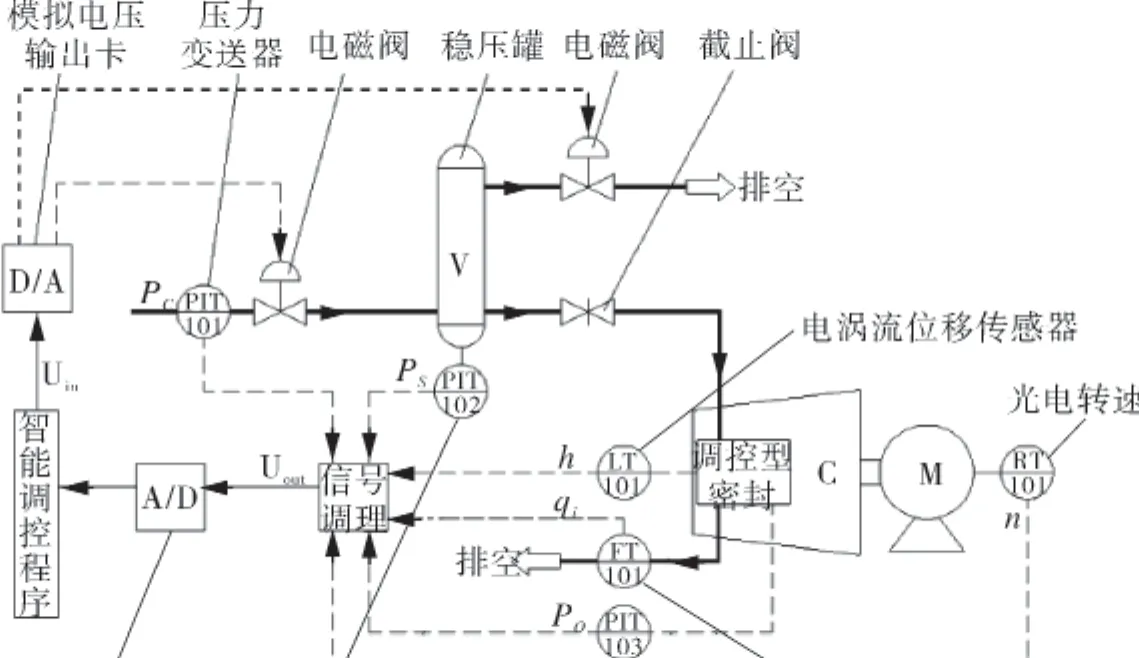
图8 密封状态调控系统流程

4.2 试验验证

本文以气膜厚度h为目标参数，通过改变试验密封装置的操作参数，通过比较目标参数与期望值符合程度，以此验证智能计算方法的精确性。

试验中，密封介质压力设为0.3MPa，取其中一组作为分析对象，依次以3组不同气膜厚度作为试验调控目标。

由图9表明，实际监测膜厚和期望膜厚有较好的匹配。试验中由于密封实际闭合力以及加工运转等因素导致膜厚结果稍有偏差，监测的实际膜厚稍大于期望膜厚。由此体现出参数智能计算程序输出的调控气压力psw值能够较好地指导调控密封，保证密封气膜厚度的稳定，验证了状态参数智能计算程序的精确性。

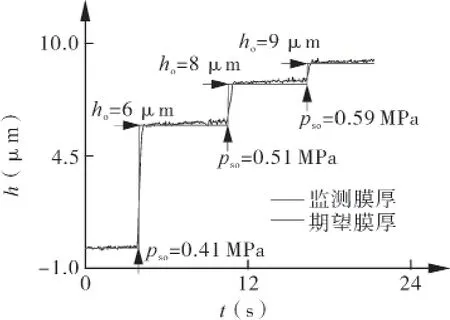
图9 智能计算程序验证

如图10所示，试验从工程现试验证了本文图3所示的调控型密封调控技术路线，直接验证了前文调压供气系统分析的正确性和参数智能计算方法的可行性与精确性。在调控过程中，系统反应时间为 Δt=t2-t1=0.8s。

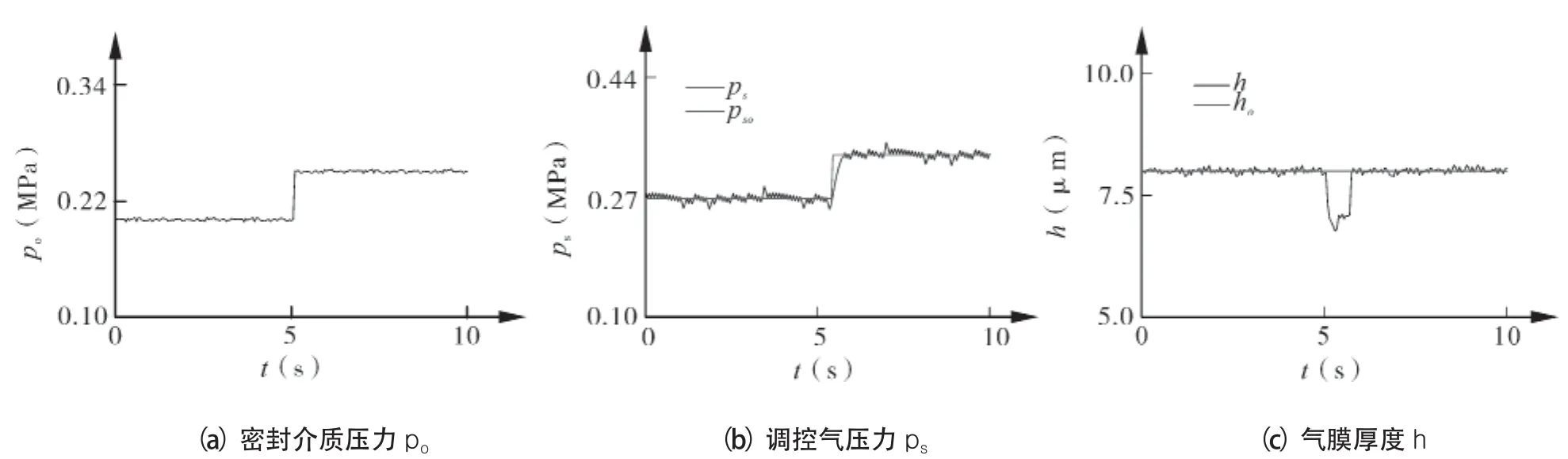
图10 以气膜为目标参数的智能计算方法验证试验

5 结论

（1）本文建立了基于PSO-BP的智能计算程序，依据研究结果综合考虑，对智能计算程序进行了优化取值：粒子群种群数量S=30，隐含层数J=1，神经元数nH=10。

（2）通过30个学习样本和10个非学习样本对智能计算程序进行误差检验，结果表明，智能计算程序计算精度均在允许范围，达到了智能化要求。

（3）采用智能计算方法对调控型气体密封参数计算，所用的计算时间均在0.013s以下，远小于数值计算方法所需时间，计算结果快速、准确，符合实际工程要求。

（4）依靠基于PSO-BP的密封状态参数智能计算方法，实现了智能调控，以气膜厚度为目标的调控反映了调控系统的响应时间是可接受的，同时试验证明了技术路线及软件的可行性。

［1］李双喜.动静压混合自愈调控气膜端面密封原理及关键技术［D］.北京 :北京化工大学 ,2011.

［2］朱亮,李双喜,张秋翔,等.主动调控型气体密封调控试验研究［J］.流体机械 ,2012,40（7）:1-6.

［3］ Nau B S. Observations and analysis of mechanical seal film characteristics ［J］. ASME Journal of Lubrication Technology, 1980, 102（3）: 341-346.

［4］ Green I, Roger M B. A simultaneous numerical solution for the lubrication and dynamic stability of noncontacting dry gas seal ［J］. ASME Journal of Transactions, 2001, 123（4）: 388-394.

［5］李双喜,宋文博,张秋翔，等.干式气体端面密封的开启特性［J］.化工学报 ,2011,62（3）:765-772.

［6］张树强,李双喜 ,蔡纪宁 ,等 .动静压混合式气体密封追随性及主动调控振动特性数值分析［J］.航空学报 ,2012（7）:1336-1346.

［7］冯向忠,彭旭东.螺旋槽干式气体端面密封性能的数值分析［J］.润滑与密封 ,2004（6）:41-43.

［8］ZhangHJ,M illerBA,LandersRG.Non linearm odelingo fm echanicalgasfacesealsystem susingp ropero rthogonaldecom position［J］.Journalo fTribo logy,2006,128（4）:817-827.

［9］戚社苗,耿海鹏,虞烈.扰动频率对动压气体轴承动态刚度和阻尼系数的影响［J］.西安交通大学学报 ,2006,40（3）:270-274.

［10］王志斌 ,陈文梅,褚良银 ,等.基于 MATLAB的BP神经网络在旋流器模拟设计中的应用［J］.流体机械,2007,35（10）:20-24.

［11］王伟,姚杨,马最良.基于BP神经网络的压缩机性能预测模型的建立［J］.流体机械 ,2005，33（9）:21-24.

［12］刘振全,佘莉芳.基于粒子群算法的涡旋压缩机涡旋盘优化的研究［J］.流体机械，2006,34（12）:25-28.

［13］彭斌，朱兵国.涡旋型线对涡旋压缩机性能的影响［J］.流体机械，2016，44（6）：17-23.

［14］朱乔峰.调控型气膜端面密封扰动性能与智能调控技术研究［D］.北京 :北京化工大学 ,2016.

Intelligent Computing Method of State Parameters for RGS Based on PSO-BP

WANG Lei, LI Shuang-xi, ZHU Qiao-feng, LI Huan
（Fluid Seal Laboratory of Beijing University of Chemical Technology, Beijing 100029, China）

As a non-contact seal，using regulatable gas seal can improve the running stability in the process of service by the introduction of intelligent control system. But the existing calculation method has many shortcomings, such as cumbersome process of establishing the calculation model or consuming time of iterative calculation. This paper proposes a BP （Back Propagation） neural network method optimized by particle swarm algorithm （PSO）, which conforms to the requirements of output accuracy and timeliness for the intelligent control system. This paper developed intelligent control procedure based on PSO-BP to control type sealing state parameter. Then optimized thresholds and weight value of neural network, and discussed impact on parameters of intelligent computing procedure such as the particle swarm population, hidden layer, and neurons several. Finally, set up the test system. The test results verified the accuracy of intelligent computing procedure of the regulatable gas seal parameters. The research realizes the intelligent control of RGS, improves anti-interference ability of RGS and contributes the large centrifugal compressor to the direction of wide working condition, high parameters, high efficiency and intelligence.

regulatable gas seal; neural network; intelligent control; state parameter

TH136；T42

A

10.3969/j.issn.1005-0329.2017.11.003

1005-0329（2017）11-0010-07

2016-07-25

2017-07-10

国家重点基础研究发展计划（973）项目（2012CB026000）

王磊（1989-），男，硕士研究生，主要从事流体密封技术方面研究，E-m ail：jasonw ang310@outlook.com。

李双喜（1977-），男，副教授，研究方向为特种密封技术，通讯地址：100029北京市朝阳区北三环东路15号北京化工大学 36 号信箱，E-m ail:buctlsx@126.com。