基本不等式知识结构与拓展
■河南省郸城县第一高级中学 彭梅荣
基本不等式知识结构与拓展
■河南省郸城县第一高级中学 彭梅荣
一、知识结构框架

二、结构分析
基本不等式是高中数学知识的难点,也是高考重点考查的知识点之一。基本不等式可以表述为:两个非负数的等差中项不小于它们的正等比中项,当且仅当两个数相等时,取得等号。基本不等式常用于求最值,解决此类问题往往需要构造两个数的和为定值或积为定值。常用的解题技巧有:添项、拆项、平方、凑系数、常值代换和分离常数等。另外,基本不等式也会与函数、数列等知识相结合进行命题,常以求参数范围、比较大小、证明不等式等形式呈现。
三、实例分析
分析:消元(消去x或y)或将x+2y视为一个整体,使用基本不等式。
解法2:由x+2y+2xy=8得,2xy=8-(x+2y)。因为2xy=x·2y≤(当且仅当x=2y时 ,等号成立),所以8-解得x+2y≥4或x+2y≤-8。又因为x>0,y>0,所以x+2y的最小值为4。
小结:以上两种解法都用到了基本不等式,容易出错的地方是解题后忘记检验等号成立的条件。解法1的突破点是消元,分离常数;解法2的突破点是将x+2y视为一个整体,构造满足基本不等式的条件。
分析:求出定点P的坐标,将其代入直线方程得m与n的关系式,常值代换后可利用基本不等式解题。
解:令x+3=1,得x=-2,所以点P坐标为(-2,1),代入直线mx-ny+4=0得2m+n=4。又因为m·n>0,所以n=2时,等号成立。

小结:已知两个变量和的形式为定值,又涉及求最小值时,往往使用常值代换,结合基本不等式求解。
变式2:设x>0,y>0,且x+3y=5xy,求3x+4y的最小值。(答案:5)
分析:分离出参数λ,把恒成立问题转化为最值问题,利用基本不等式求最值。
解:因为a,b∈R,所以可以分三种情况进行讨论:
(1)当b(a+b)=0时,λ∈R。
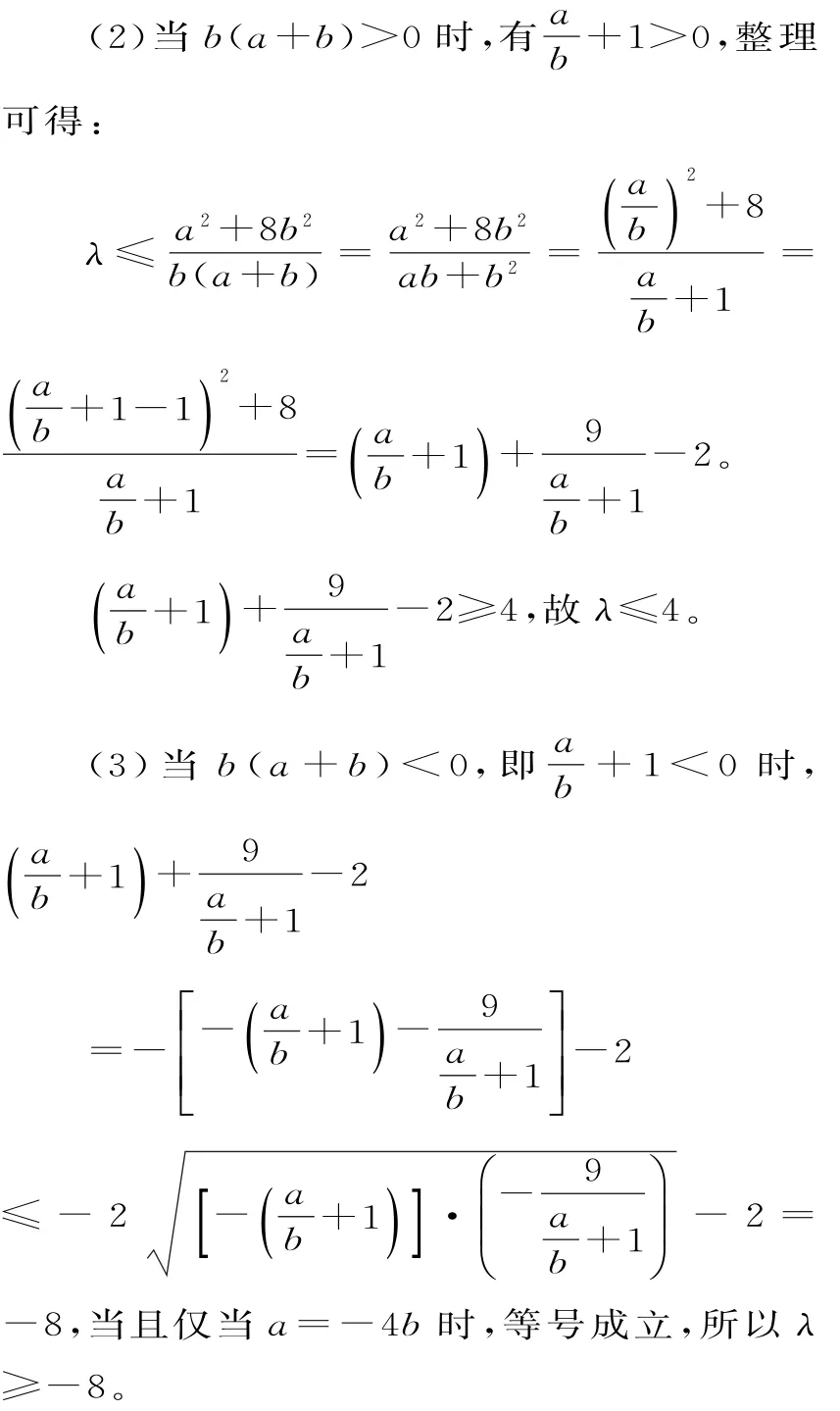
综上,实数λ的取值范围为-8≤λ≤4。
小结:本题容易出错的地方:一是忽略对b(a+b)的符号进行讨论,二是忽略使用基本不等式的前提条件(一正、二定、三相等)。另外恒成立问题和有解问题也是高中数学的重要题型,两者均转化为求最值问题,求最大值还是最小值,要结合不等式的方向来看。
分析:可以先对所求式子平方,消元,拼凑系数,然后利用基本不等式求解。

小结:解决本题的关键是将所求式子平方消元,最容易错的地方是最后结果忘记开方。当两个变量有某种关系时,可考虑消元,消元后发现式子的和为定值,可以考虑用基本不等式求最值。另外,对本题也可平方,消元,然后将x2视为一个整体,利用二次函数求最值。
四、跟踪练习
1.当x∈(0,1)时,求函数y=x·(1-x)2的最大值。
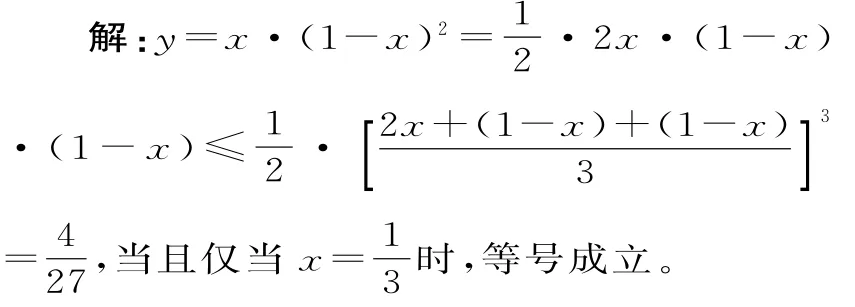
函数y=x·(1-x)2的最大值为
小结:求解本题的关键是将(1-x)2看成(1-x)·(1-x),拼凑系数后可以发现三个数的和为定值,而求的是它们积的最大值,此时可以考虑用不等式。
(责任编辑 徐利杰)

