新疆兵团农机总动力预测模型的研究
刘银萍,陈永成,曹卫彬,毕新胜
(石河子大学 机械电气工程学院,新疆 石河子 832000)
新疆兵团农机总动力预测模型的研究
刘银萍,陈永成,曹卫彬,毕新胜
(石河子大学 机械电气工程学院,新疆 石河子 832000)
为了提高新疆兵团农机总动力预测模型的精度,获得更加可靠的预测结果,针对回归模型的多重共线性问题及灰色模型仅含有指数增长趋势的问题,基于2007-2014年农机动力的相关数据,建立了主成分回归和灰色回归两种预测模型。对两种模型的预测精度进行比较分析,结果表明:主成分回归模型和灰色回归模型预测值的平均相对误差分别为0.57%、0.46%,灰色回归预测模型的精度较高,可以较真实地反映新疆兵团农机总动力的变化趋势。应用该模型进行预测,得到了新疆兵团农机总动力未来5年的预测值。
农机总动力;预测模型;主成分回归模型;灰色回归模型
0 引言
农机总动力是指用于农、林、牧、渔业各种动力机械的动力总和,是反映农业机械化水平的重要指标,预测农机动力的发展情况,对农业机械化水平的评价、农机发展规划的制定及农业生产力的提高具有重要意义。
目前,常用的预测方法有回归分析法、灰色预测法、指数平滑法、人工神经网络法及移动平均法等[1]。这些方法都有各自的优点和不足,得到的预测结果也有一定的差异[2-3]。例如,程敬春[4]采用灰色GM(1,1)模型对新疆农机总动力进行了预测,得到了2011-2015年动力的预测值,模型的精度达到了97%。刘静[5]选取多个影响因素建立多元线性回归模型对我国农机总动力进行预测,得到了我国2000-2010年农机总动力的预测值,模型的平均相对误差为0.91%。上述模型虽然可以取得比较好的预测结果,但是单独使用均存在一定的缺陷,如多元线性回归模型可以综合考虑多种因素对因变量的影响,从而得到更加全面的分析结果;但一些自变量可能彼此相关,过多的变量不仅会使计算变得复杂,而且会对预测结果的可靠性造成影响[6]。灰色GM(1,1)模型可以从农机总动力数据本身着手,分析数据的变化规律,预测未来发展趋势,无需考虑其他影响因素,计算简便、预测精度高。但是,GM(1,1)模型主要适用于单一的指数增长序列,对于序列出现的异常情况通常无法解决[7]。
为了提高模型的预测精度,本文综合上述不同模型的优缺点,对多元线性回归模型和灰色GM(l,1)模型进行改进优化。首先,为了全面分析多种因素对农机总动力的影响,并解决因素间的相关性问题,本文通过提取主成分建立回归方程得到主成分回归预测模型。同时,为了分析农机总动力数据本身的变化规律,改善原GM(l,1)模型中不含线性因素以及线性回归模型中不含指数增长趋势的情形[7],本文特建立了灰色回归预测模型。其次,为了获得更加可靠地预测结果,对两种模型的预测精度进行比较,选择精度较高的模型对新疆兵团农机总动力未来5年的发展情况进行预测。
1 主成分回归模型的建立
1.1 主成分回归模型的构建原理
在农机动力预测的研究中,为了综合考虑多种因素对农机总动力的影响、解决由于各因素间彼此相关造成的多重共线性问题及提高预测精度,本文采用主成分回归分析法建模。利用主成分分析法构造原变量的线性组合得到互不相关的新变量,然后提取主成分建立回归模型。其具体步骤为:
1)首先,对p个影响因素X1,X2,…,Xp进行标准化处理,得到标准化影响因素ZX1,ZX2,…,ZXp,然后进行主成分分析,得到p个因素的线性组合F1,F2,…,Fp,再根据累计贡献率提取前m个主成分F1,F2,…,Fm。
2)采用最小二乘法,以m个主成分F1,F2…,Fm为自变量,以新疆兵团农机总动力Y为因变量做多元线性回归,得到回归模型为
3)将上述回归模型进行转化,可得原始变量X和动力Y的回归模型为
1.2 新疆兵团农机总动力主成分回归预测模型建立
1.2.1 新疆兵团农机总动力及其影响因素原始数据
为了研究新疆兵团农机的发展情况,通过查阅相关文献,并且对众多影响因素做相关性分析,从中选取了7个主要影响因素。现取兵团农机总动力Y为因变量,国民经济生产总值X1、第一固定资产投资X2、大中型拖拉机保有量X3、耕地总面积X4、棉花总产量X5、团场劳动力X6及机械收割面积X7为自变量进行分析,由《新疆生产建设兵团统计年鉴》可得统计数据,如表1所示。

表1 2007-2014年新疆兵团农机总动力相关统计数据
1.2.2 主成分分析结果
利用MatLab软件对7个影响因素的原始数据进行标准化处理,然后对标准化数据进行主成分分析,结果如表2所示。
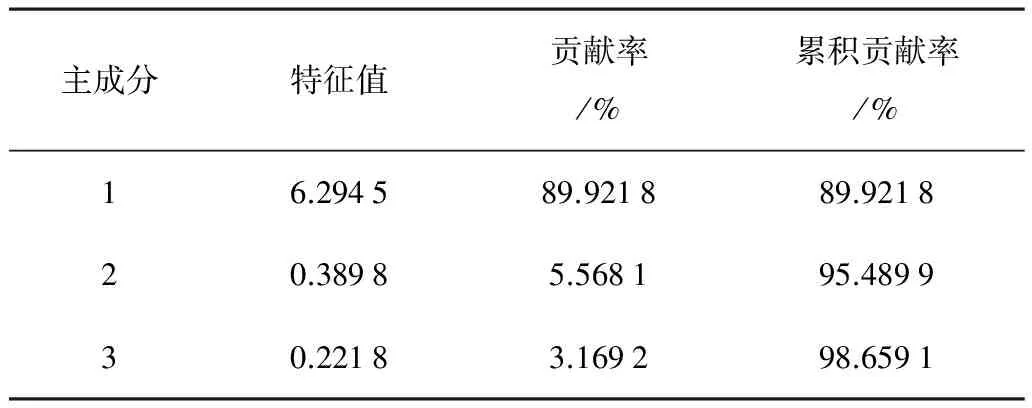
表2 主成分提取结果
由表2可以看出:第一主成分的特征根为6.294 5,贡献率达89.921 8%。但是,根据实际情况,本文在保证降维的同时也要保证主成分回归预测模型的精度,因此,本文提取前3个主成分,其累计贡献率为98.659 1%。
提取的前3个主成分与其表达式分别为
F1=0.3940ZX1+0.3882ZX2+0.3766ZX3+
0.3620ZX4+0.3541ZX5+0.3909ZX6+
0.3782ZX7
(1)
F2=0.1031ZX1-0.3018ZX2+0.4801ZX3-
0.0077ZX4-0.6509ZX5-0.1309ZX6+
0.4763ZX7
(2)
F3=0.2795ZX1-0.0844ZX2+0.1603ZX3-
0.8760ZX4+0.3143ZX5+0.0308ZX6+
0.1483ZX7
(3)
1.2.3 提取主成分,建立回归方程
以F1,F2,F3为自变量,以标准化后的总动力ZY为因变量建立多元线性回归方程,可得
ZY=0.3873F1+0.2892F2+0.3150F3
(4)
其中,相关系数R2=0.998 6,F=965.843 2,大于理论值,显著性P=3.561 8×10-6远小于0.05,t=(52.33 65,9.727 2,7.990 8)也均大于理论值,并且回归系数的显著性P=(0.000 0,0.001 2,0.003 2)均小于0.05。因此,可以认为回归方程的拟合优度很好,模型高度显著。这说明所选取的影响因素国民经济生产总值、第一固定资产投资、大中型拖拉机保有量、耕地总面积、棉花总产量、团场劳动力及机械收割面积可以很好地反应新疆兵团农机总动力的发展情况。
1.2.4 转化为原始变量,建立主成分回归方程
联立式(1)~式(4)可以得到标准化变量的回归方程为
ZY=0.2704ZX1+0.0365ZX2+0.3352ZX3-
0.1379ZX4+0.0478ZX5+0.1232ZX6+
0.3309ZX7
(5)
将式(5)转化为原始自变量表示的主成分回归方程为
Y=141.3415+0.0376X1+0.0755X2+0.0026X3-
0.1406X4+0.1871X5+1.8468X6+0.1112X7
(6)
2 灰色回归模型的建立
2.1 灰色回归模型的构建原理

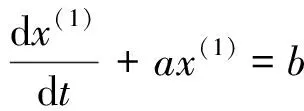
(7)
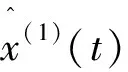
(8)
其中,参数v及C1、C2、C3待定。
2.2 灰色回归模型的参数确定
为了确定以上参数,设参考序列为
t=1,2,…,n-1
(9)
并且设
ym(t)=z(t+m)-z(t)=
C1evt(evm-1)(ev-1)
(10)
同理可得
ym(t+1)=C1ev(t+1)(evm-1)(ev-1)
(11)
式(10)、式(11)两式的比为
ym(t+1)/ym(t)=ev
(12)
由此可以得到v的解为
v=ln[ym(t+1)/ym(t)]
(13)
(14)

(15)

则有
X(1)=AC
(16)
C=(ATA)-1ATX(1)
(17)
从而得到一次累加序列的预测模型为
(18)
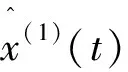
2.3 灰色回归模型的精度检验
求出预测模型后,需要对模型的精度进行检验,本文采用后验差检验法对灰色回归模型的c(后验差)和p(小误差概率)进行检验,其计算公式为
(19)
其中
2.4 新疆兵团农机动力灰色回归预测模型的建立
1)由表1中的数据可建立原始序列X(0),有
X(0)={303.5325,318.3161,338.5588,
369.3346,396.2558,424.3602,458.7234,484.1622}
对X(0)做一次累加可得序列X(1)得
X(1)={303.5325,621.8486,960.4074,
1329.7420,1725.9978,2150.3580,2609.0814,
3093.2436}
-13657.3969)。所以,预测模型为
将数据带入式(19)进行计算可得,c=0.0345<0.35,p=1>0.95,所以此模型的精度等级为一级[9],可用来做农机动力预测。
3 模型精度及预测结果分析
1)利用主成分回归模型和灰色回归模型对2007-2014年新疆兵团农机总动力进行预测,预测结果如表3所示。
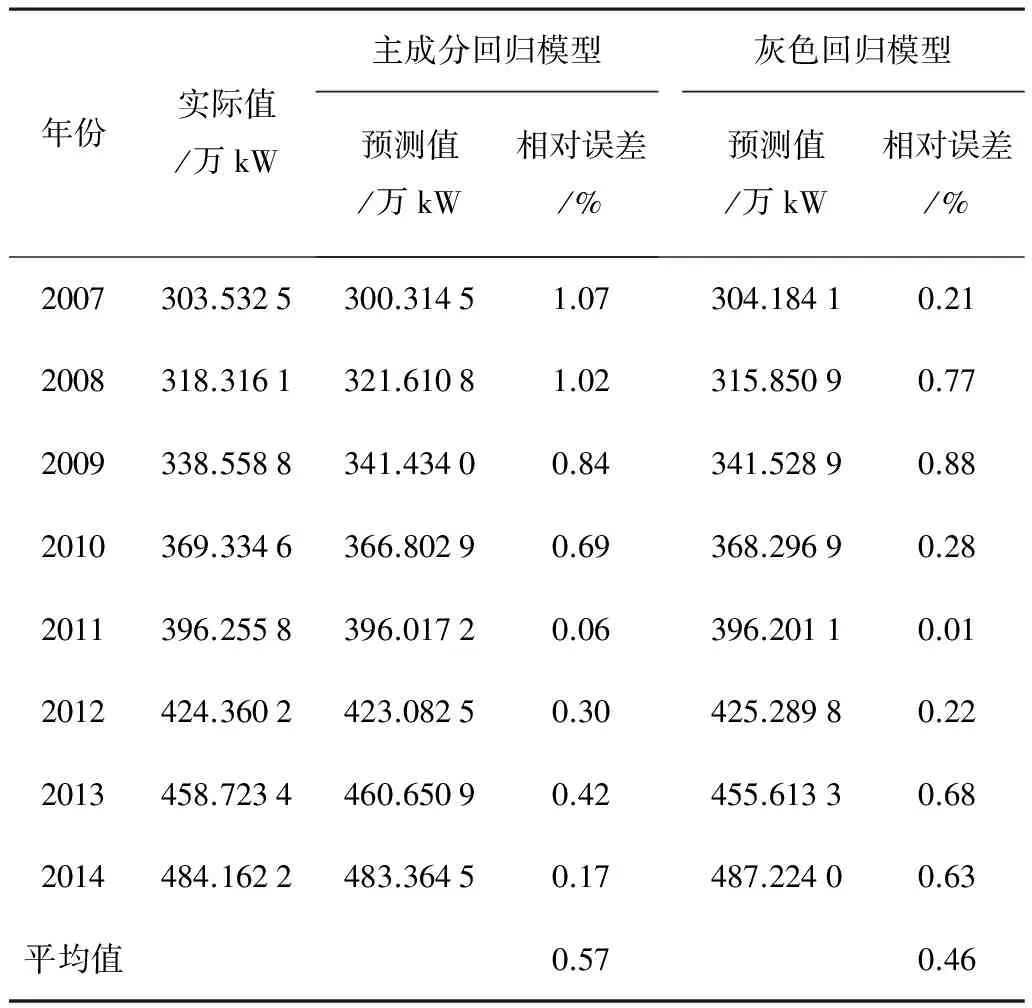
表3 两种模型的预测结果比较
从表3中可以看出:主成分回归预测模型虽然受多种因素的影响,但仍达到了较高的预测精度,其最大相对误差为1.07%,最小相对误差为0.06%,平均相对误差为0.57%。灰色回归预测模型以农机总动力数据序列为基础建立模型,能够很好地反映数据的变化规律,所以预测精度高于主成分回归模型,最大相对误差为0.88%,最小相对误差为0.01%,平均相对误差为0.46%。因此,本文采用灰色回归模型对新疆兵团农机总动力的未来发展情况进行预测。
2)采用灰色回归模型对2015-2019年的新疆兵团农机总动力进行预测,其预测结果如表4所示。
从表4中可以看出:新疆兵团农机总动力未来5年呈稳步上升的趋势,2019年总动力将达到666.581 0万kW,比2014年增长37.68%。由此可知:随着我国农业现代化的发展以及农机补贴政策的日渐成熟,新疆兵团农业机械化水平将会不断地提高,农机总动力必然会不断增加。
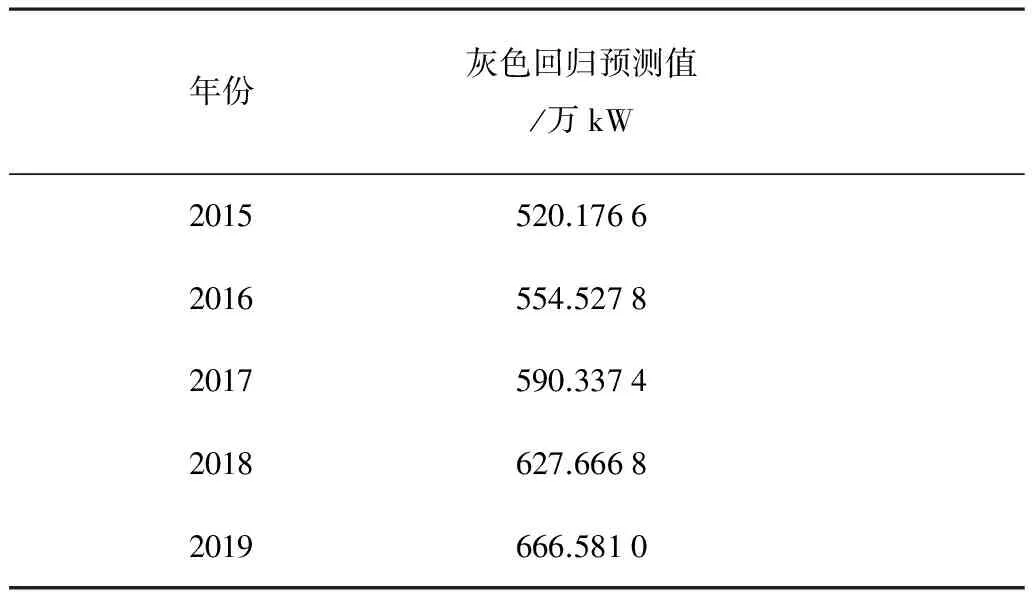
表4 2015-2019年新疆兵团总动力预测结果
4 结论
1)建立了主成分回归和灰色回归两种模型对新疆兵团农机总动力进行预测,均取得了较好的预测效果。其中,主成分回归预测模型综合考虑了多个影响因素并且消除了多重共线性的影响,F检验和t检验均获得了较高的显著性,模型的精度较高。灰色回归预测模型综合利用了灰色模型和回归模型的有用信息,较真实地反映了动力数据本身的变化规律,采用后验差法检验模型等级为一级,精度较高,可用来做农机动力预测。
2)对两种模型的精度进行对比分析,结果表明:主成分回归模型和灰色回归模型的精度分别为99.43%和99.54%,灰色回归模型的预测精度更高,具有较好的适用性和科学性,可以作为一种新疆兵团农机总动力预测的新方法。
3)采用灰色回归模型对新疆兵团农机总动力未来5年的发展情况进行预测,得到2015-2019年农机总动力的预测值分别为520.176 6、554.527 8、590.337 4、627.666 8、666.581 0万kW。
[1] 陈华友,周礼刚,刘金培.数学模型与数学建模[M].北京:科学出版社,2014:224-230.
[2] 白丽,李行,马成林.2005-2015年吉林省农机化作业水平定量预测[J].农业机械学报,2005,36(9):64-67.
[3] 陈丽能,谢永良.基于BP神经网络的农机拥有量预测技术[J].农业机械学报,2001,32(1):118-121.
[4] 程敬春,杨宛章,张刘洁.运用GM(1,1)模型对新疆农机总动力发展状况预测[J].新疆农机化,2012(1):26-28.
[5] 刘静,朱达荣.考虑自变及因变影响的农机总动力组合预测模型[J].农机化研究,2015,37(4):230-236.
[6] 李毛侠.安徽省消费需求影响因素的主成分回归分析[J].现代物业,2010,9(2):48-51.
[7] 侯丽敏,马国锋.基于灰色线性回归组合模型铁路客运量预测[J].计算机仿真,2011,28(7):1-3.
[8] 王慧勇,晏秋.基于灰色线性回归组合模型的高速公路交通量预测[J].交通运输工程与信息学报,2016,14(1):53-57.
[9] 曹建莉,肖留超,程涛.数学建模与数学实验[M].西安:西安电子科技大学出版社,2014:183-192.
Research on the Prediction Model of Agricultural Machinery Total Power in Xinjiang Corps
Liu Yinping, Chen Yongcheng, Cao Weibin, Bi Xinsheng
(Mechanical and Electrical Engineering College,Shihezi University,Shihezi 832000,China)
In order to improve the precision of forecast model of agricultural machinery total power in Xinjiang corps and obtain more reliable predictions, focus on the problems of regression model of multicollinearity and grey model containing only exponential growth trend,based on the data of 2007 to 2014 related to agricultural power,established principal component regression and gray regression model.The prediction accuracy of the two models were compared, and the results showed that the average relative error of predicted values of the principal component regression model and grey regression model were 0.57% and 0.46%.The gray regression prediction model is of high precision and can truly reflect the change of agriculture machinery total power of Xinjiang corps. The model is applied to forecast and obtained the forecast value of agricultural machinery total power of xinjiang corps in the next five years.
total power of agricultural machinery; forecast model; principal component regression model; gray regression model
2016-05-26
国家自然科学基金项目(51445015)
刘银萍(1990-),女,河南宁陵人,硕士研究生,(E-mail)969723515@qq.com。
陈永成(1958-),男,河南南阳人,教授,硕士生导师,(E-mail) 604295294@qq.com。
S232.3
A
1003-188X(2017)07-0034-05

