基于结构化噪声矩阵补全的WSNs收集数据重建方法

陈正宇 陈 蕾 胡国兵 戴 华

(1．金陵科技学院电子信息工程学院, 南京, 211169； 2.江苏省无线传感网高技术研究重点实验室, 南京,210003；3.南京邮电大学计算机学院,南京,210003)

基于结构化噪声矩阵补全的WSNs收集数据重建方法

陈正宇1陈 蕾2, 3胡国兵1戴 华3

(1．金陵科技学院电子信息工程学院, 南京, 211169； 2.江苏省无线传感网高技术研究重点实验室, 南京,210003；3.南京邮电大学计算机学院,南京,210003)

许多科学研究都需要对环境数据进行分析，这些环境数据通常是通过部署在研究区域内的无线传感器网络(Wireless sensor networks, WSNs)来收集的。收集数据的完整性和准确性决定了科研结果的可靠性。然而，在数据收集过程中普遍存在的数据丢失和错误影响了收集数据的可用性，为此需要利用收集到的数据重建完整的环境数据。基于环境数据低秩特性，将数据重建问题建模为L2,1范数正则化矩阵补全模型，提出一种基于结构化噪声矩阵补全的WSNs收集数据重建方法(Data reconstruction approach via matrix completion with structural noise, DRMCSN)。真实数据集上的实验结果表明，该方法性能优于现有算法，不仅能以较高的精度恢复缺失的环境数据，而且能辨识出收集到错误数据的传感器节点。

无线传感器网络；数据收集；矩阵补全；数据重建

引 言

无线传感器网络(Wireless sensor networks, WSNs)在环境资源监测、节点定位、基础设施监测和生物习性监测等科学研究场景中得到了广泛的应用[1,2],而数据收集通常是实现这些应用的基础环节。但由于受到传感器节点硬件特性、资源条件、无线通信和部署环境等因素的制约，在数据收集过程中通常会出现数据丢失和数据错误等问题[3,4]。例如，在Intel室内实验项目中，研究人员通过3个星期的观察发现有近40%的数据丢失和8%的数据错误[4]。数据丢失和错误给相关应用的准确性和可靠性带来了巨大的挑战[5]。因此，利用WSNs收集到的含有错误元素的不完整数据集来重建原始环境数据具有十分重要的意义。

近年来，矩阵补全技术越来越受到研究者的普遍关注。矩阵补全技术能通过存在元素缺失的不完整数据矩阵重构出原始的完整低秩矩阵,目前，已在推荐系统、图像处理、标记分类、网络监测和WSNs等领域中得到广泛的应用[6]。在WSNs领域中，数据采集、节点定位等应用场景已利用矩阵补全技术来恢复缺失的数据信息。在数据收集应用场景中，为了减少WSNs数据收集能耗,文献[7]提出一种有效数据收集方法(Efficient data collection approach, EDCA)，该方法只收集网络中部分节点采集的环境数据，从而得到一个不完整的环境数据矩阵，然后利用环境数据矩阵的低秩特性将数据恢复问题建模成缺失数据矩阵的补全问题，并设计优化算法解决该问题。由于该方法仅利用矩阵的低秩特性，因此在数据丢失严重的情况下，重建误差仍然较大。文献[8]利用收集数据矩阵的低秩和瞬时稳定性特征，提出空时压缩数据收集方法(Spatiotemporal compressive data collection, STCDC)，瞬时稳定性在求解矩阵补全问题的最优解时提供稳定性约束，从而降低了环境数据的重建误差。文献[9]分析了WSNs收集数据丢失模式，并利用收集数据的低秩、时间和空间相关性等特征，提出基于时空提升的环境数据重建方法(Environmental space-time improved compressive sensing, ESTI-CS)算法，结合秩最小估计以及时空特征恢复丢失数据。文献[10]提出联合矩阵补全和稀疏约束的数据恢复方法(Data recover method with joint matrix completion and sparsity constraints, DRMCSC)，利用数据的稀疏特征和矩阵的低秩特性，将稀疏约束和矩阵补全结合在同一优化问题中，并设计交替最小化算法实现数据重建。以上算法仅考虑恢复丢失数据的问题，均没有考虑数据错误问题以及其对数据恢复精度的影响。而已有的研究通常利用数据相关性和统计特性来检测错误数据,比如文献[11,12]分别提出基于直方图和基于收集数据统计特性的Outlier数据检测方法;文献[13]提出利用序列检测方法识别传感器网络中的错误数据;文献[14]研究异常收集数据和链路中断的存在对数据收集精确度的影响，并基于压缩感知理论识别和纠正异常收集数据。然而，上述错误数据检测算法都没有考虑数据缺失对于错误数据检测性能的影响。

对于不完整低秩数据矩阵的重建问题，文献[15]提出当不完整的低秩数据矩阵中的某些行受到损坏时，传统矩阵补全算法恢复性能往往显得不够稳定，为此将不完整矩阵中受到损坏的行看作是数据行受到结构化噪声的污染，并将存在这类噪声情形的矩阵补全问题称为结构化噪声矩阵补全问题。文献[16]将结构化噪声矩阵补全问题应用于Web服务的QoS预测中。受到文献[15,16]的启发，本文针对WSNs数据采集过程中同时存在的数据丢失和数据错误等问题，提出一种基于结构化噪声矩阵补全的WSNs收集数据重建方法(Data reconstruction via matrix completion with structural noise, DRMCSN)。该方法将错误数据建模为收集数据受到行结构化噪声的污染，利用环境数据矩阵的低秩特性，将含有错误收集数据情况下的环境数据重建问题建模为结构化噪声矩阵补全模型，并利用文献[15]提出的矩阵空间交替线性分裂Bregman迭代算法实现该问题的求解。仿真实验表明，DRMCSN能以较高的精度恢复缺失数据，同时能辨识出收集到错误数据的传感器节点。

1 预备知识

1.1 基本定义

假设矩阵X∈Rn1×n2的奇异值分解为X=UΣVT，其中，Σ=diag{σi|1≤i≤min(n1,n2)且σ1≥σ2≥…≥σmin(n1,n2)>0}，则有如下定义[15]

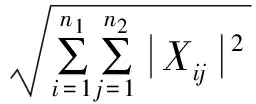
1.2 相关定理

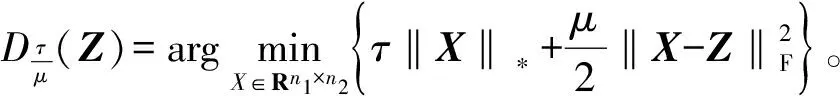
定理2[18]近邻前向后向分裂(Proximal forward backward splitting, PFBS)。对于无约束优化问题

(1)

假定J(X)是Rn1×n2上具有下半连续性质的凸函数，H(X)是Rn1×n2上凸光滑下半连续函数且具有β-Lipschitz连续导数，即 {‖H(X1)-H(X2)‖F≤β{‖X1-X2‖F,∀X1,X2∈Rn1×n2，则对任意的初始值X0及0<δ<，用如式(2)生成的迭代序列Xk+1收敛到无约束优化问题(1)的唯一解为

Xk+1=proxδJ(X)(Xk-δ

(2)

定理1，2和3的证明可分别详见文献[16-18]。

2 系统模型与问题描述

2.1 系统模型

设监测区域内部署N个传感器节点v1,v2,…,vN，周期性地收集环境数据。将每轮收集时间间隔称为一个时隙。设收集总时间为T个时隙，则对于某一类环境数据，总数据量为N×T。该环境数据可用矩阵X表示为

(3)

式中：X(i,j)表示节点vi对应于时隙j的原始环境数据。然而，由于收集过程中存在数据丢失，Sink节点得到的是一个有很多元素丢失的不完整矩阵，也称为采样矩阵，用S表示；将收集到的数据称为采样数据；将采样数据占总数据量的比例称为数据采样率。

定义Ω⊆[N]×[T]([N]={1,…,N}，T={1,…,T})为采样数据在采样矩阵中的下标索引集合。ΡΩ(·)为正交投影算子，表示当(i,j)∈Ω时，S(i,j)为采样元素，即有

(4)

由于存在数据错误，采样数据可能有两种情况，即原始环境数据X(i,j)和错误数据F(i,j)。采样数据S(i,j)可表示为

(5)

错误数据F(i,j)可表示为原始环境数据与噪声值的叠加，即

F(i,j)=X(i,j)+Z(i,j)

式中：Z(i,j)为噪声值。将收集到的错误数据的传感器节点称为故障节点，将故障节点所占的比例称为节点故障率。在实际应用中，某些传感器节点容易成为故障节点，这些节点在采样矩阵中所对应的数据行含有错误元素。对于这类行元素的错误问题，可视为采样矩阵受到行形式的结构化噪声的污染，进一步可将采样矩阵表示为

ΡΩ(S)=ΡΩ(X+Z)

(6)

式中：Z=(Z(i,j))N×T为行形式的结构化噪声矩阵。在矩阵Z中，如果节点vi在时隙j收集到错误数据，则Z(i,j)≠0，否则Z(i,j)=0。

2.2 问题描述

WSNs收集数据的重建问题就是利用Sink节点收集到的采样矩阵S来重建原始环境数据矩阵X。利用环境数据矩阵的低秩特性，可以将数据重建问题建模为矩阵补全问题[7,8]。在求解矩阵补全问题时，为了有效地平滑结构化噪声，将噪声矩阵Z的L2,1范数正则化项引入到标准矩阵补全问题中[16]，从而将含有错误数据的无线传感器网络收集数据重建问题建模为基于L2,1范数正则化的结构化噪声矩阵补全模型，即有

s.t.ΡΩ(S)=ΡΩ(X+Z)

(7)

式中：S为采样矩阵，X为优化矩阵，Z为结构化噪声矩阵，λ为一个用来平衡结构化噪声和矩阵低秩程度的可调参数。求解矩阵补全问题(7)得到的最优解Xopt和Zopt可以用来重建环境数据矩阵Xrec。

3 基于结构化噪声矩阵补全的数据重建方法

基于第2节提出的系统模型，本节将给出DRMCSN算法的具体实现方法。首先，将问题(7)松弛为无约束优化问题，即

(8)

问题(8)不存在解析解。基于文献[15]提出的矩阵空间交替线性分裂Bregman迭代算法，可将问题(8)转化为求解2个子问题，即

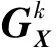
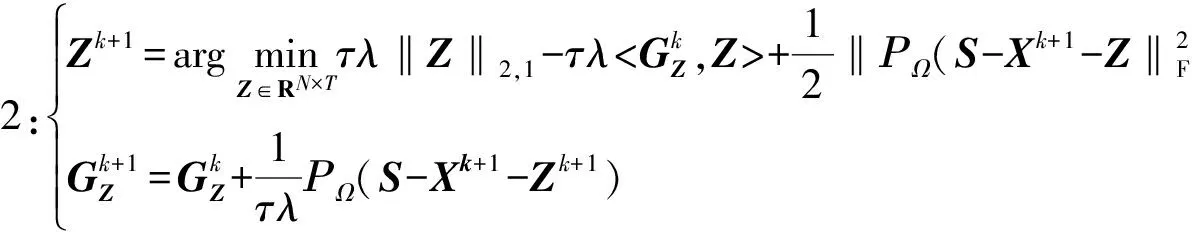
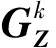
(1)求解子问题1

Xk+1=proxδXJ(X)(Xk-δXH(Xk))=

(9)

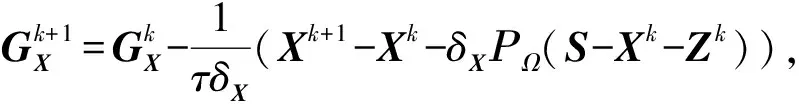
(10)

根据定理1可得

Xk+1=DτδX(Vk)

(11)

因此，子问题1可按式(12)迭代求解

(12)

式中参数δX可作如式(13)的估算，即

{‖H(X1)-H(X2)‖F={‖ΡΩ(X1+Zk-S)-ΡΩ(X2+Zk-S)‖F=

{‖ΡΩ(X1-X2)‖F≤1·{‖X1-X2‖F

(13)

(2)求解子问题2

类似于子问题1的求解过程，可得

(14)

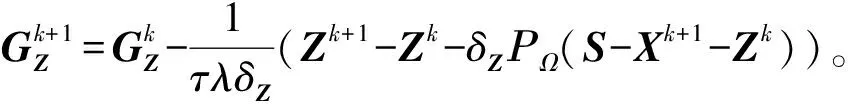
(15)

根据定理3可得

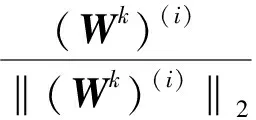
(16)

因此，子问题2可求解为

(17)

基于子问题1和子问题2的求解方法，在确定算法最大迭代次数等参数后，可以得到矩阵补全问题(7)的最优解，即恢复的数据矩阵Xopt和恢复的噪声矩阵Zopt。利用矩阵Xopt和Zopt可以重建环境矩阵Xrec，具体方法包括以下两个步骤：

(1)用恢复的数据矩阵Xopt中的对应元素Xopt(i,j)来填充采样矩阵S中丢失的元素，即重建环境矩阵Xrec满足

(18)

(2)通过恢复的噪声矩阵Zopt识别故障节点。在Zopt中，含有非零元素的行所对应的传感器节点为故障传感器节点；所有元素为0的行所对应的传感器节点为正常传感器节点。在识别出故障器节点后，可将重建环境矩阵Xrec中含错误数据的行用恢复数据矩阵Xopt中所对应的行替代，即

(19)

综上，可以给出基于结构化噪声矩阵补全的数据重建方法(DRMCSN)如算法1所示，其中输入为无线传感器网络采样数据矩阵ΡΩ(S)，最大迭代次数Max以及各类参数，如λ，τ等；输出为重建数据矩阵Xrec。算法首先设置初值矩阵为零矩阵(第1行)，第3～4行求解子问题1，5～8行实现子问题2的求解，11～22行实现环境数据的重建。

算法1基于结构化噪声矩阵补全的数据重建方法(DRMCSN)

输入：数据收集矩阵ΡΩ(S)，λ，τ，δX和δZ，最大迭代次数Max;

输出：Xrec;

初始化X0=0,Z0=0,V-1=0,W-1=0;

FORk=0 to MAX

Vk=Vk-1+δXΡΩ(S-Xk-Zk);

Xk+1=DτδX(Vk);

Wk=Wk-1+δZΡΩ(S-Xk+1-Zk);

FORi=1 toN

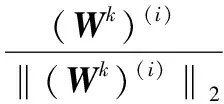
END FOR

END FOR

Xopt=XMax+1;Zopt=ZMax+1;

FORi=1 toN

FORj=1 toT

IF(i,j)∈Ω

Xrec(i,j)=S(i,j);

ELSE

Xrec(i,j)=Xopt(i,j); /*填充丢失的元素*/

END IF

END FOR

END IF

END FOR

4 仿真实验

4.1 实验条件

为了评估算法性能，采用Intel室内项目中采集的温度数据作为实验数据。选取52个传感器节点在连续300个时隙中采集的温度数据构建原始环境数据矩阵XN×T，其中N=52，T=300。利用XN×T合成得到用于实验的采样矩阵SN×T，合成步骤为

(1)根据数据采样率，产生随机的采样数据下标索引集合Ω。依据Ω从原始环境数据矩阵XN×T中采样元素，得到合成数据矩阵SN×T，满足

(20)

(2)基于传感器节点故障率，确定故障节点数m，从SN×T中随机选取m行，并将这m行中50%的非零元素叠加随机噪声Zij。假设错误数据的下标索引集合为。最终得到合成的采样矩阵SN×T，满足

(21)

式中：Zij是均值为0，方差为δ2的正态分布随机变量，即Zij～N(0,δ2)。

执行算法1后，通过重建数据矩阵Xrec和原始环境数据矩阵XN×T的对比来衡量算法性能。对于λ和τ等可调参数自适应设置的理论研究还没有展开，本文依据所处理问题的先验知识对其进行交叉验证。

4.2 性能参数定义

(1)丢失数据恢复误差εm，表示恢复丢失环境数据的精确程度。εm可以表示为

(22)

式中：Ω′表示丢失数据下标索引集。

(23)

式中：E为故障节点集合，E′为正常传感器节点集合。X(i,j)满足：i,j:i∈E′∩(i,j)∈Ω′，表示正常传感器节点丢失的数据；X(i,j)满足：i,j:i∈E,1≤j≤T表示故障传感器节点对应的数据行。

4.3 仿真结果和分析

将DRMCSN算法与STCDG[8]和DRMCSC[10]进行对比分析，用于对比的数据为15次随机实验结果的平均值。图1给出了在不同数据采样率的情况下，丢失数据恢复误差的性能对比。在实验中，设置节点故障率为40%，数据采样率在5%到95%之间。为便于观察，将恢复误差通过图1(a,b)两张图片呈现。如图1所示，数据采样率越低，所有算法对丢失数据恢复误差越大。在数据采样率为5%时，STCDG和DRMCSC算法的恢复误差接近60%，而DRMCSN算法不到30%。可见在数据采样比较低的情况下，DRMCSN算法明显优于其他两个算法，而且采样率越低，DRMCSN算法的优势越明显。随着采样率的升高，所有算法的恢复误差都逐渐降低。在数据采样率比较高的情况下，几种算法恢复误差都较小，但是DRMCSN算法性能还是明显优于其他算法。DRMCSN算法减少了数据错误对丢失数据恢复误差的影响，从而带来了性能上的优势。

图2给出了不同节点故障率的条件下，丢失数据恢复误差的性能对比，其中设置数据采样率为50%，传感器节点故障率从10%递增到90%。随着故障传感器节点数量的增加，所有算法对缺失元素的恢复误差随之增加，但DRMCSN始终优于其他算法，并且当传感器节点故障率较高时，DRMCSN的优越性更加明显。图2反映了错误数据的存在对丢失数据恢复误差的影响程度。STCDG和DRMCSC算法由于没有考虑错误数据的存在，因此恢复误差受到的影响较大，而DRMCSN算法中引入的噪声矩阵的L2,1范数平滑了错误数据的影响，从而丢失数据恢复误差相对较小。

在不同故障率的条件下，数据重建误差性能对比如图3所示，其中数据采样率为50%，传感器节点故障率从10%到90%。从图3可见DRMCSN算法性能明显优于其他算法，其主要原因为：(1)由图2可知DRMCSN算法由于减少了错误数据的影响，从而对丢失数据的恢复误差优于其他算法；(2)由于STCDG和DRMCSC算法不能识别故障传感器节点，不能对错误数据行进行替换，因此对应的数据重建误差大，而DRMCSN能够识别故障节点，并能对错误数据行进行替换，从而对错误数据行的重建性能优于其他算法。

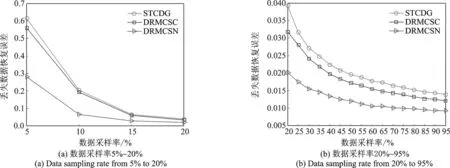
图1 不同数据采样率下的丢失数据恢复误差Fig.1 Recovery error of missing data under different sampling rate

图2 不同故障率下丢失数据恢复误差 图3 不同故障率下数据重建误差Fig.2 Recovery error of missing data under different faulty rates Fig.3 Reconstruction error under different faulty rates

5 结束语

无线传感器网络数据收集过程数据丢失和错误等问题普遍存在。数据的丢失和错误影响了收集数据的可用性和准确性，因此本文提出一种基于结构化噪声矩阵补全的无线传感器网络收集数据重建方法。该方法旨在从含有错误数据元素的不完整收集数据中重建环境数据。将数据错误建模为原始环境数据受到结构化噪声的污染，进一步利用环境数据矩阵低秩特性，从而将无线传感器网络收集数据重建问题建模为结构化噪声矩阵补全问题，并基于矩阵空间交替线性分裂Bregman迭代算法实现该问题的求解。实验结果表明，该方法可以显著提高环境数据的重建精度，并可以识别采集到错误数据的传感器节点。本文的后续工作将包括利用收集数据矩阵的时间和空间相关性进一步提升数据恢复精度等。

[1] 李正周, 缪鹏飞, 刘勇,等. 基于无线传感器网络的大型场所火情检测与定位算法[J]. 数据采集与处理, 2014, 29(6):964-969.

Li Zhengzhou, Mou Pengfei, Liu Yong, et al. Fire detection and position algorithm for large room based on wireless sensor network[J].Journal of Data Acquisition and Processing, 2014, 29(6):964-969.

[2] 朱志宇, 苏岭东. 基于分布式粒子滤波的二进制无线传感器网络目标跟踪[J]. 数据采集与处理, 2015，30(3):564-570.

Zhu Zhiyu, Su Lingdong. Target tracking based on distributed particle filtering in binary wireless sensor network[J].Journal of Data Acquisition and Processing, 2015，30(3):564-570.

[3] Xie K, Ning X, Wang X, et al. Recover corrupted data in sensor networks: A matrix completion solution[J]. IEEE Transactions on Mobile Computing, 2017,16(5):1434-1448.

[4] Kamal A R M, Bleakley C, Dobson S. Packet-level attestation (PLA): A framework for in-network sensor data reliability [J]. ACM Transaction on Sensor Networks, 2013, 9(2): 1-19.

[5] Koushanfar F, Potkonjak M. Markov chain-based models for missing and faulty data in MICA2 sensor motes[C]//The 4th IEEE conference on Sensors. Irvine, California, USA:IEEE, 2005:1430-1434.

[6] 陈蕾,陈松灿.矩阵补全模型及其算法研究综述[J].软件学报,2017,28(6):1547-1564.

Chen Lei, Chen Songcan. Survey on matrix completion models and algorithms[J]. Journal of Software, 2017,28(6):1547-1564.

[7] Cheng Jie, Jiang Hongbo, Ma Xiaoqiang, et al. Efficient data collection with sampling in WSNs: Making use of matrix completion techniques [C]//2010 IEEE Global Communications Conference. Miami, Florida, USA:IEEE, 2010: 1-5.

[8] Cheng Jie, Ye Qiang, Jiang Hongbo, et al. STCDG: An efficient data gathering algorithm based on matrix completion for wireless sensor networks[J].IEEE Transaction on Wireless Communication, 2013, 12(2):850-861.

[9] Kong Linghe, Xia Mingyuan, Liu Xiaoyang, et al. Data loss and reconstruction in sensor networks[C]//International Conference on Computer Communiations．Turin, Italy:IEEE, 2013: 1654-1662.

[10] He Jingfei, Sun Guiling, Zhang Ying, et al. Data recovery in wireless sensor networks with joint matrix completion and sparsity constraints [J].IEEE Communications Letters, 2015, 19(12):2230-2233.

[11] Sheng Bo, Li Qun, Mao Weizhen et al. Outlier detection in sensor networks[C]//The 8th ACM International Symposium on Mobile Ad Hoc Networking and Computing (MobiHoc)．Montreal, Quebec， Canada： ACM， 2007:219-228.

[12] Ding Min， Cheng Xiuzhen. Robust event boundary detection in sensor networks—A mixture model based approach[C]//International Conference on Computer Communications. Rio de Janeiro, Brazil：IEEE, 2013: 2991-2995.

[13] Guo Shuo, Zhong Ziguo, Chen Jiming, et al. Detecting faulty nodes with data errors for wireless sensor networks[J]. ACM Transactions on Sensor Networks, 2014, 10(3):1-27.

[14] Tang Yu, Zhang Bowu, Jing Tao, et al. Robust compressive data gathering in wireless sensor networks[J]. IEEE Transactions on Wireless Communications, 2013, 12(6): 2754-2761.

[15] 陈蕾, 杨庚, 陈正宇,等. 基于线性Bregman迭代的结构化噪声矩阵补全算法[J].计算机学报, 2015(7):1357-1371.

Chen Lei, Yang Geng, Chen Zhengyu, et al. Linearized bregman iteration algorithm for matrix completion with structural noise[J]. Chinese Journal of Computer, 2015, 38(7):1357-1371.

[16] 陈蕾, 杨庚, 陈正宇, 等. 基于结构化噪声矩阵补全的Web服务QoS预测[J].通信学报, 2015, 36(6):49-59.

Chen Lei, Yang Geng, Chen Zhengyu, et al. Web services QoS prediction via matrix completion with structural noise[J].Journal on Communications, 2015, 36(6):49-59.

[17] Cai Jianfeng, Candes E J, Shen Z. A singular value thresholding algorithm for matrix completion[J]. SIAM Journal of Optimization, 2010, 20(4): 1956-1982.

[18] Combettes P L, Wajs V R. Signal recovery by proximal forward-backward splitting[J]. Multiscale Modeling and Simulation, 2005, 4(4): 1168-1200.

DataReconstructioninWSNsviaMatrixCompletionwithStructuralNoise

Chen Zhengyu1, Chen Lei2,3, Hu Guobing1, Dai Hua3

(1.School of Electronic and Information Engineering, Jinling Institute of Technology, Nanjing， 211169, China;2. Jiangsu High Technology Research Key Laboratory for Wireless Sensor Networks, Nanjing， 210003, China； 3. College of Computer Science & Technology, Nanjing University of Posts &Telecommunications, Nanjing， 210003, China)

Many scientific work needs to analyze the environmental data which are usually collected by wireless sensor networks(WSNs)deployed in research areas. The integrity and accuracy of the collected data determine the reliability of the research results. However, data loss and error usually occur during the process of data collection, which affect the availability of collected data. Therefore, it is necessary to reconstruct the environmental data from the incomplete and erroneous sensory data. Based on the low-rank feature of the environmental data, an efficient data reconstruction approach via matrix completion with structural noise (DRMCSN) is proposed by formulating data reconstruction problem as aL2,1-norm regularized matrix completion model. Finally, experimental results on a real dataset demonstrate that the proposed approach can not only effectively reconstruct the environmental data, but also recognize the sensor nodes that collect erroneous data.

wireless sensor networks; data collection; matrix completion; data reconstruction

江苏省自然科学基金(BK20130096,BK20161516,BK20161104)资助项目;国家自然科学基金(61300240,61572263)资助项目;江苏省高校自然科学基金(15KJB520027)资助项目;中国博士后科学基金(2015M581794)资助项目;江苏省博士后科研资助计划(1501023C)资助项目;安徽省自然科学基金(1608085MF127)资助项目;金陵科技学院高层次人才工作启动(JIT-201527)资助项目。

2017-07-26；

2017-09-21

TP311

A

陈正宇(1978-)，男，博士，副教授，研究方向：无线传感器网络、机器学习和信号与信息处理，E-mail: zych@jit.edu.cn。

陈蕾(1975-)，男，博士，副教授，研究方向：机器学习、服务计算和信息安全。

胡国兵(1978-)，男，博士，副教授，研究方向：数字信号处理、认知无线电等。

戴华(1982-)，男，博士，副教授，研究方向：数据管理与安全、数据库安全等。