二次雷达混扰信号的迭代投影分选算法
刘 垒 张 玉 唐 波
(电子工程学院504教研室,合肥,230037)
二次雷达混扰信号的迭代投影分选算法
刘 垒 张 玉 唐 波
(电子工程学院504教研室,合肥,230037)
针对二次雷达应答信号混扰导致解码错误的问题,提出一种迭代投影分选算法。综合考虑天线结构、残留载频等因素建立阵列信号混扰模型,通过对模型中待求变量的最大似然估计分析,给出双矩阵变量优化模型,以非圆复信号快速独立成分分析(Noncircular complex fast independent component analysis, nc-FastICA)算法得到应答信号初始值,进而根据二次雷达应答信号零/恒模(Zero/constant modulus, ZCM)特性提出迭代投影分选算法,最终完成对混扰信号的分选。仿真结果表明,在应答机之间相距较近、天线非精确调整等复杂环境下,本算法可从混扰应答信号中有效地分选出各应答信号,且分选性能明显优于快速独立成分分析算法。
二次雷达;盲分选;混扰信号;迭代投影
引 言
二次监视雷达在空中交通管制系统中发挥着不可替代的作用,其可通过解码应答信号,获取空中目标的高度、方位和代码等信息。实际应用中,模式A/C在复杂的电磁环境中极易受到干扰,模式S虽然抗干扰性能优于模式A/C[1,2],但随着空中交通流量的高速增长,当询问天线波束内存在多个目标时,询问机可以收到询问天线波束内多个应答机的应答信号,造成信号混扰,严重影响信号的模式识别和解码[3,4],降低了二次雷达系统的安全性和可靠性。
目前国内外针对二次雷达混扰信号分选的解决方案主要有旋转不变因子技术(Estimation of signal parameters via rotational invariance techniques, ESPRIT)、独立成分分析(Independent component analysis, ICA)算法、特征矩阵联合近似对角化(Joint approximative diagonalization of eigenmatrix, JADE)算法和曼彻斯特解码算法(Manchester decoding algorithm, MDA)等[5-10]。文献[5]提出了基于多通道阵列处理的分选方法,通过ESPRIT算法估计应答信号到达方向(Direction of arrival, DOA),进而反推引导矩阵,该算法能够对DOA进行较精确的估计,具有较好的分选性能,但其要求二次雷达询问机使用精确调整后的均匀线性阵列天线来接收应答信号,算法存在一定的局限性。文献[8]提出了基于最小残量优化算法的分选方法,对引导矩阵和应答信号矩阵进行寻优处理,并把独立的优化问题转换为搜索问题,从而完成分选,克服了ESPRIT算法中需要精确调整天线的局限性,但由于搜索所需的定义域矩阵较大,运算量相对较大。文献[9]提出了MDA算法,该算法巧妙地利用了模式S应答信号的曼彻斯特编码特性来构建分选模型,适用于当混扰信号中只存在模式S信号时的情形,但计算复杂度较高。
由于接收机和应答机之间存在频率差以及不可避免的多普勒频移现象,在应答信号下变频之后,仍存在残留载频,并非原始基带信号,相当于基带应答信号与未知的复指数相乘,由实信号变为复信号,但下变频后的应答信号仍保持其本身所具有的零/恒模(Zero/constant modulus,ZCM)特性。本文提出一种基于二次雷达信号ZCM特性的迭代投影分选算法,实现了对二次雷达信号的有效盲分选。首先建立了阵列天线任意分布情况下的阵列信号混扰模型和双矩阵变量优化模型,并采用非圆复信号快速独立成分分析算法[6,11]得到应答信号初始值,进而以迭代投影分选算法完成对二次雷达混扰信号的分选,最后通过仿真验证了本文算法的有效性。
1 阵列信号混扰模型和优化模型
二次雷达系统中模式S是在模式A/C的基础上发展起来的,询问信号和应答信号的载波频率分别为1 030 MHz和1 090 MHz,上行链路和下行链路使用不同的载频,可以有效地避免两者间发生混淆。目前西方发达国家正逐渐使用模式S取代模式A/C,我国模式S还未广泛应用[12]。本文所建立的阵列信号混扰模型和优化模型同时兼容这两种模式的应答信号。
1.1 阵列信号混扰模型
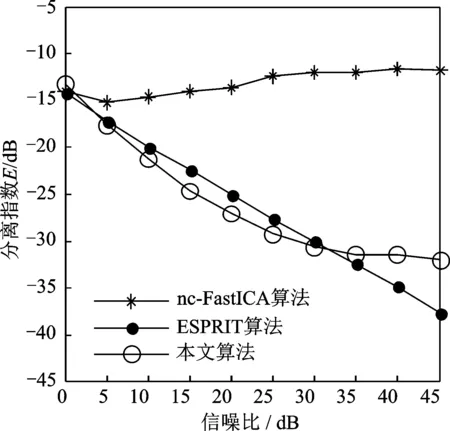
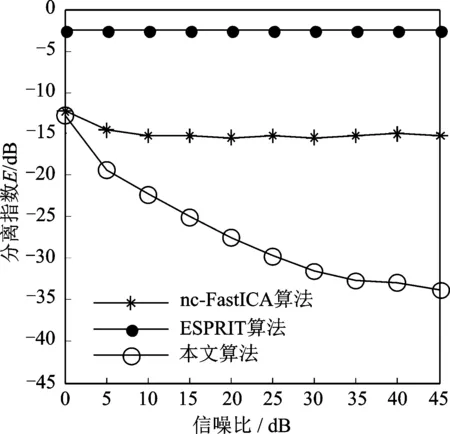
假设天线阵元数为M,进入接收机的应答信号个数为K,且K Y=AS+V (1) 应答信号载波频率标称值fc=1 090 MHz,接收到的信号实际中心频率为fu,下变频后的残留载频为Δf=fc-fu,国际民航组织规定|Δf|≤3 MHz。残留载频将导致信号的相位旋转,接收到的信号经下变频处理后,以采样率1/TS对其进行采样,则在采样点n(n=1,2,…,N)处的采样信号可以表示为 (2) 式中:rk[n]为信号源k的第n个应答信号码字,取值为0或1,具有ZCM特性;φk=exp(j2πΔfkTS)。 应答信号矩阵S可表示为 (3) 式中:⊙表示矩阵Hadamard积。 显然sk[n]仍然具有ZCM特性[13],即 |sk[n]|=0 或 |sk[n]|=1 (4) 若询问机的接收天线为均匀线阵,阵元间距为半波长,且天线经精确校正,则阵列引导矢量ak为 (5) 式中:θk为应答信号sk相对于阵列法线的入射角度。然而,在现实中引导矩阵A会受到多方面因素影响[14],如不精确的阵列天线刻度、天线耦合和阵列混扰等。因此,本文仅假设引导矩阵A为列满秩复矩阵,即天线可以为线阵、圆阵、面阵或三维空间任意分布的阵列,且未精确调整,仅要求阵元数大于信号源数。 假设vm(m=1,2,…,M)服从零均值,方差为σ2的白复高斯分布,且相互独立,则混扰信号ym服从均值为amS,协方差矩阵为σ2IN的复高斯分布,其中am为引导矩阵A的行矢量。ym的概率密度函数表示为 (6) 则y1,y2,…,yM的联合概率密度为 (7) 可采用最大似然估计方法对应答信号矩阵S进行估计,则为了使似然函数最大,应使式(8)最小 (8) 注意到 (9) 即似然函数最大时,矩阵Y-AS的Frobenius范数应取最小值。故而从混扰信号矩阵Y中分选出应答信号矩阵S的问题可转换为如下的双矩阵变量优化问题 (10) 式中A和S均为待优化的未知量。对信号进行盲分选的目的是为求出使代价函数最小的优化变量A和S。 采用迭代投影分选算法求解式(10)中的优化问题,首先要得到应答信号矩阵S和引导矩阵A的初始值,然后采用迭代投影分选算法,在每一步迭代中又涉及到两个子优化问题:(1)固定应答信号矩阵S求解引导矩阵A;(2)固定引导矩阵A求解应答信号矩阵S。 在文献[15]中给出二次雷达信号的圆性分析,模式S应答信号近似为圆复信号,模式A/C应答信号为非圆复信号,文献[11]中提出的去噪nc-FastICA算法,是将FastICA算法的使用范围从圆复信号扩充到非圆复信号,既适用于非圆复信号也适用于圆复信号,所以综合运算复杂度和性能方面的考虑,采用去噪nc-FastICA算法对应答信号矩阵S的初始值进行估计。 估计应答信号矩阵S之前,首先要对信源数进行估计,本文采用最小描述长度(Minimum description length, MDL)准则估计应答信号个数[16,17]。该算法从信息论的角度出发,可对信源数进行有效估计,即 (11) 式中:λ为样本协方差矩阵CY=(1/L)YYH的特征值且按由大到小顺序排序,λi为第i个大的特征值。 以去噪nc-FastICA算法估计应答信号矩阵S的初始值,基本步骤为: (1) 对混扰信号矩阵Y进行中心化,使其均值为零; (3) 取分离矩阵W的列矢量wk; (12) (5) 正交化 (13) (6) 判断W是否收敛,若未收敛,重新令k=1,并返回(3),此处判断收敛条件可取更新误差; 当应答信号矩阵S固定时,式(10)可以改写为如下优化问题 (14) 式(9)可写为 (15) 将式(15)对引导矩阵A求导,并令求导结果为0,可得 (16) 即应答信号矩阵S固定时的最优引导矩阵A是方程Y=AS的最小二乘解。 所以引导矩阵A的初始估计值为 (17) 求解固定引导矩阵A时的应答信号矩阵S,可以采用分而治之的思想。注意到 (18) 因此优化问题可以分解为K个较为简单的优化问题,第k(k=1,2,…,K)个优化问题可以表示为 s.t. |sk[n]| = 0或1;n= 1,2,…,N (19) 令Yr=Y-A(k)S(k),则式(19)可以写为 s.t. |sk[n]| = 0 或 1;n= 1,2,…,N (20) 注意到,优化问题gk又可以分解为N个独立的优化问题。第n个待求解的优化问题可表达为 s.t.|sk[n]| = 0 或 1 (21) 式中:yr为Yr的列向量。 sk[n]=0 (22) 当应答信号的幅度为1时,将代价函数展开为 (23) 当且仅当sk[n]满足下式条件时,式(23)中的等号成立。 (24) 所以,gk,n的最优解为 (25) 通过估计得到引导矩阵A后,可以进一步对应答信号到达角进行估计,第k个应答信号的DOA估计值为 (26) 基于二次雷达信号ZCM特性的迭代投影分选算法步骤为: 第一步:通过MDL准则估计应答信号个数; 第三步:迭代投影 (a) 令k=1; (c) 利用式(25)计算sk[n]; (d)n←n+1,若n≤N返回(c); (f)k←k+1,若k≤K返回(b); 以文献[6]中的分离指数IA作为分选性能评价指标,亦即 (27) 分选算法的分选效果主要受不同应答信号到达角差值、信噪比和天线是否精确校正等因素的影响,先分别从这些角度出发,将本文迭代投影算法与ESPRIT算法和nc-FastICA算法的分选性能进行对比。假设天线阵元数为M= 10,使用1/TS= 60 MHz的采样频率对下变频后的信号进行数字采样,采样区间长度为75 μs,仿真结果取1 000次独立蒙特卡罗实验的平均值。 为了与ESPRIT算法作比较,假设天线为精确调整后的均匀线性阵列天线,阵元间距为半波长,且不考虑天线耦合、多通道延时等因素,引导矩阵A=[a1,a2,…,aK],其列矢量ak(k=1,2,…,K)可由式(5)求得,通过仿真得到混扰信号,然后分别以nc-FastICA算法、ESPRIT算法和本文迭代投影算法对混扰信号进行分选,比较其分选性能。 首先固定信噪比为20 dB,考虑有2个模式S应答信号进入到询问机的情况,两者具有不同的延时,DOA范围取[-20°,20°]。固定其中一个应答信号的DOA值为-2°,另一个应答信号的DOA值相对变化,变化区间取1°至14°。图1比较了两个应答信号DOA差值不同时,本文迭代投影算法与nc-FastICA算法和ESPRIT算法DOA估计值的均方根误差(Root mean squared error, RMSE)。DOA估计值的RMSE可定义为 (28) 从图1中可以直观地看出,在天线精确调整的情况下,ESPRIT算法在DOA估计方面具有明显优势,其RMSE随着DOA差值的增加单调下降,具有较好的角度分辨力;本文算法DOA估计性能优于nc-FastICA算法,可以进行有效的DOA估计,但两者性能均差于ESPRIT算法。 图2为3种算法的分离指数曲线,可以清晰地发现,本文迭代投影算法对混扰信号的分选性能整体相对较好,尤其是当DOA差值较小,即两个应答机之间的距离较小时,本文算法仍保持较好的分选性能,随着DOA差值的增加分离指数趋于稳定;ESPRIT算法的分离指数随着DOA差值的增加单调减小,在DOA差值较大时,分选性能最优;而nc-FastICA算法的分离指数在DOA差值变化时无明显变化,分选性能相对较差。 图1 均匀线阵不同DOA差值情况下DOA估计的RMSE比较 Fig.1 RMSE of DOA estimations under different DOA difference in uniform linear array 图2 均匀线阵不同DOA差值情况下算法的分选性能 Fig.2 Separation performance of algorithms under different DOA difference in uniform linear array 固定两个信号的DOA为-3°和2°,两信号的信噪比从0 dB变化到45 dB,3种算法的分离指数比较如图3所示。可以看出本文迭代投影算法和ESPRIT算法相对于nc-FastICA算法均具有较好的分选性能,且信噪比在5 dB与30 dB之间时,本文算法的分选性能为三者最优;随着信噪比的增加,本文算法的分离指数趋于稳定,ESPRIT算法的分离指数单调减小。 分析天线阵元任意分布的情况,考虑引导矩阵A受到多方面因素影响,假设其为仅满足列满秩的复值矩阵,此情况下不能对DOA进行有效估计,ESPRIT算法失效。考虑有4个应答信号进入到询问机,包括1个模式A/C应答信号和3个模式S应答信号,且四者具有不同的延时,4个信号的信噪比从0 dB变化到45 dB。图4为3种算法的分离指数比较,可以看出ESPRIT算法分选失败,本文算法和nc-FastICA算法仍可以对信号进行分选;当信噪比大于10 dB时,nc-FastICA算法的分离指数几乎不发生变化,即随着信噪比的增加nc-FastICA算法分选的性能并没有提高;当信噪比小于35 dB时,本文迭代投影分选算法的分离指数随着信噪比的增加单调下降,当信噪比大于35 dB时,分离指数趋于稳定,易见本文迭代投影算法的分选性能明显优于nc-FastICA算法。 图3 均匀线阵不同信噪比情况下算法的分选性能 Fig.3 Separation performance of algorithms under different SNR in uniform linear array 图4 非均匀线阵不同信噪比情况下算法的分选性能 Fig.4 Separation performance of algorithms under different SNR in non-uniform linear array 本文以迭代投影分选算法实现了对二次雷达混扰信号的有效分选。文中建立了阵列信号混扰模型,在建模过程中充分考虑了天线结构、残留载频等因素;通过对模型中待求变量的最大似然估计分析,提出了双矩阵变量优化模型;根据二次雷达应答信号的ZCM特性提出了双矩阵变量迭代优化算法。仿真结果表明,阵列天线精确调整的情况下,在DOA估计方面ESPRIT算法性能最优,本文算法亦可有效地估计DOA;在信号分选方面,当应答机之间距离较小时,本文算法仍保持较好的分选性能;在阵列天线未精确调整的情况下,ESPRIT算法完全失效,而本文算法仍可以对二次雷达混扰信号进行有效盲分选,且分选性能明显优于nc-FastICA算法。 [1] 张尉.二次雷达原理[M]. 北京: 国防工业出版社, 2009: 9-12. [2] 王洪, 刘昌忠, 汪学刚. 二次雷达 S 模式综述[J]. 电讯技术, 2008, 48(7): 113-118. Wang Hong, Liu Changzhong, Wang Xuegang. Mode S for secondary surveillance radar (SSR): An introduction and overview[J]. Telecommunication Engineering, 2008, 48(7): 113-118. [3] Galati G, Bartolini S, Menè L. Analysis of SSR signals by super resolution algorithms[C]∥Proceedings of the Fourth IEEE International Symposium on Signal Processing and Information Technology. Roma:IEEE, 2004: 166-170. [4] 王洪, 刘昌忠, 汪学刚, 等. 强干扰背景下 S 模式解码方法[J]. 电子与信息学报, 2009, 31(12): 2876-2880. Wang Hong, Liu Changzhong, Wang Xuegang, et al. Mode S decoding methods in heavy jamming environment[J]. Journal of Electronics & Information Technology, 2009, 31(12): 2876-2880. [5] 唐波, 程水英, 张浩. 基于多通道阵列处理的二次雷达混扰信号分选[J]. 电讯技术, 2014, 54(5): 534-540. Tang Bo, Cheng Shuiying, Zhang Hao. Separation of garbled secondary surveillance radar signal based on multichannel array processing[J]. Telecommunication Engineering, 2014, 54(5): 534-540. [6] Novey M, Adali T. On extending the complex FastICA algorithm to noncircular sources[J]. IEEE Transactions on Signal Processing, 2008, 56(5): 2148-2154. [7] Petrochilos N, Van der Veen A J. Algebraic algorithms to separate overlapping secondary surveillance radar replies[J]. IEEE Transactions on Signal Processing, 2007, 55(7): 3746-3759. [8] 张玉, 樊斌斌, 胡进, 等. 基于最小残量优化算法的二次雷达信号分选[J]. 现代雷达, 2015, 37(4): 46-49,54. Zhang Yu, Fan Binbin, Hu Jin, et al. Separation of secondary surveillance radar signal based on MINRES optimization algorithm[J]. Modern Radar, 2015, 37(4): 46-49,54. [9] Petrochilos N, Piracci E G, Galati G. Improved MDA, a case for de-garbling SSR mode S replies[C]∥IEEE Tyrrhenian International Workshop on Digital Communications-Enhanced Surveillance of Aircraft and Vehicles (TIWDC/ESAV).Roma:IEEE, 2014: 87-91. [10] Galati G, Petrochilos N, Piracci E G. Degarbling mode S replies received in single channel stations with a digital incremental improvement[J]. IET Radar, Sonar & Navigation, 2015, 9(6): 681-691. [11] 阮宗利, 李立萍, 钱国兵, 等. 基于含噪复值 ICA 信号模型的快速不动点算法[J]. 电子与信息学报, 2014, 36(5): 1094-1099. Ruan Zongli, Li Liping, Qian Guobing, et al. Fast fixed-point algorithm based on complex ICA signal model with noise[J]. Journal of Electronics & Information Technology, 2014, 36(5): 1094-1099. [12] 兰鹏, 曾一江, 王陵. S 模式地面二次监视雷达及其关键技术分析[J]. 电讯技术, 2012, 52(6): 840-845. Lan Peng, Zeng Yijiang, Wang Ling. Ground mode S secondary surveillance radar and its key techniques analysis[J]. Telecommunication Engineering, 2012, 52(6): 840-845. [13] Van der Veen A J, Tol J. Separation of zero/constant modulus signals[C]∥IEEE International Conference on Acoustics Speech and Signal Processing (ICASSP).Munich:IEEE, 1997: 3445-3448. [14] Petrochilos N, Galati G, Piracci E. Separation of SSR signals by array processing in multilateration systems[J]. IEEE Transactions on Aerospace and Electronic Systems, 2009, 45(3): 965-982. [15] Petrochilos N, Comon P. A zero-cumulant random variable and its applications[J]. Signal Processing, 2006, 86(11): 3334-3338. [16] Rissanen J. Modeling by shortest data description[J]. Automatica, 1978, 14(5): 465-471. [17] 黄桂根, 孟兵, 李品. 一种基于 MDL 原理的信号分选新算法[J]. 数据采集与处理, 2015, 30(3): 656-668. Huang Guigen, Meng Bing, Li Pin. New radar signal deinterleaving algorithm based on MDL criterion[J]. Journal of Data Acquisition and Processing, 2015, 30(3): 656-668. IterativeProjectionAlgorithmtoSeparateGarbledSecondarySurveillanceRadarReplies Liu Lei, Zhang Yu, Tang Bo (504 Research Office, Electronic Engineering Institute, Hefei, 230037, China) To overcome the problem of decoding errors of secondary surveillance radar (SSR) due to the phenomenon of garble, an iterative projection algorithm for separating the garbled replies is proposed. Firstly, a signal model for the garbled replies is established in which the influence factors such as antenna structure, residual carrier frequency and so on are taken a full consideration, and an optimization model with double matrix variables is proposed based on the maximum likelihood estimation of the unknown variable in the model. Then, the initial value of replies is estimated by the algorithm of noncircular complex fast independent component analysis (nc-FastICA). And then, the iterative projection algorithm based on the zero/constant modulus (ZCM) property of SSR replies is proposed to separate garbled SSR replies. Numerical simulations show that the proposed method can separate multiple replies accurately in the complex environment such as shorter distance of the transponders and inaccuracy in the antenna and so on, and it outperforms the algorithm of nc-FastICA obviously in the separation performance. secondary surveillance radar (SSR); blind signal separation (BSS); garbled replies; iterative projection 国家自然科学基金(61671453, 61201379)资助项目;安徽省自然科学基金(120805QF103)资助项目。 2016-03-02; 2016-09-06 TN958.96 A 刘垒(1990-),男,硕士研究生,研究方向:信号与信息处理,E-mail:songshiliulei@163.com。 张玉(1962-),男,教授,研究方向:雷达与通信中的信号处理。 唐波(1985-),男,讲师,博士,研究方向:自适应阵列信号处理、雷达波形设计等。
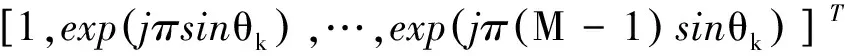
1.2 基于双矩阵变量优化的分选问题建模

2 迭代投影分选算法
2.1 估计初始值

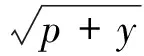
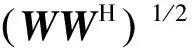
2.2 固定应答信号矩阵求解引导矩阵

2.3 固定引导矩阵求解应答信号矩阵



2.4 分选步骤



3 仿真分析

3.1 仿真实验1




3.2 仿真实验2
4 结束语




