基于推理公式法的小流域洪水计算灵敏度分析

艾力江·克力木

基于推理公式法的小流域洪水计算灵敏度分析

艾力江·克力木

（塔里木河流域喀什管理局，新疆 莎车 844700）

为了提升小流域洪水计算的精确性，需要对影响小流域洪水灵敏度的因素进行精确研究。基于推理公式法，以叶尔羌河为例，对小流域洪水相关指标的灵敏度进行分析，分析了不同参数变化的影响程度对洪水计算灵敏度的影响。相关分析结果对提升小流域洪峰流量计算的精度有重要意义。

叶尔羌河；小流域防洪；科学防洪；灵敏度分析

在对洪水灵敏度进行分析过程中，能够运用的方法较多，比如一院两所法、林平一法、瞬时单位线法、推理公式法以及经验公式法等。我国水文精确普及的程度较低，小流域的暴雨资料、实测径流等有关资料较为缺乏，许多参数需要通过经验估计、地形特征对比等方式来选取。因此，不同的参数值选择会对洪水计算结果产生影响。接下来，基于推理公式法，以叶尔羌河为例，对不同参数及其变化对计算结果灵敏度进行分析，希望能够对识别不同参数变化的影响程度有更加清晰的认知，从而改善叶尔羌河洪水监测及计算的合理性、精确性有积极意义。

1 推理公式法概述

在计算洪峰时，如果根据流域内降雨资料求取，则可以对很多条件进行概化处理，提升计算结果的条件性。这种洪水计算方法被称为推理公式法，又被称为稳定形势公式或者合理化计算方法，它在500km2内小流域洪水的计算中较为适用。

在计算小流域洪峰流量时，采用如下所示的公式。

为了求取流域产流情况，需要对tc与τ的关系进行探讨。

当tc＞τ时，可以通过下式求取流域全面产流：

当tc＜τ时，可以通过下式求取流域部分产流：

式中，Qm—洪峰设计流量，m3/s；ψ—洪峰设计径流系数；Sp—设计频率 p下的降雨力度，mm/h；H24p—频率 p下、24h内的流域最大雨量，mm；Kp—模比系数；τ—汇流时间，h；τ0— ψ=1情形下的汇流时间，h；n—流域内暴雨的衰减指数，可以通过分区统计表查阅而得；F—流域面积，km2；tc—产流形成所经历的时间，h；μ—平均入渗系数，mm/h；m—汇流参数，结合该地区水文情况，可以通过表1查阅确定。

2 推理公式法参数灵敏度分析

以叶尔羌河6～8月工况为例，进行小流域洪水计算灵敏度分析。6月工况为算例1，此时的流域特征值为：F=136.3km2，L=38.37km，J=9‰，汇流参数 m=1.3，流域损失参数 μ=2.3mm/h，最大降雨量H24，1%=325.7mm，雨衰减指数 n1=0.55，n2=0.70。7月工况为算例2，此时的流域特征值为：F=136.3km2，L=38.37km，J=9‰，最大降雨量 H24，1%=323.9mm，汇流参数m=0.749，μ=3.5mm/h，雨衰减指数n1=0.5，n2=0.7。8月工况为算例3，此时的流域特征值为：F=136.3km2，L=38.37km，J=9‰，流域损失参数 μ=3.5mm/h， 最大降雨量 H24，1%=202mm， 汇流参数 m=1.1，雨衰减指数n1=0.60，n2=0.75。

表1 汇流参数m值查用表

2.1 损失参数μ的灵敏度分析

损失参数μ发生变化时，洪峰流量Q也可能相应地发生变化，变化灵敏度计算公式为：

首先，对算例1进行计算。对μ进行扰动，相关指标值会发生变化，变化情况见表2、图1。

图1 Qμ随μ扰动的变化图

接着，对算例2进行计算。对μ进行扰动，相关指标值会发生变化，变化情况如表3、图2所示。

表3 Qμ随μ扰动的计算结果表

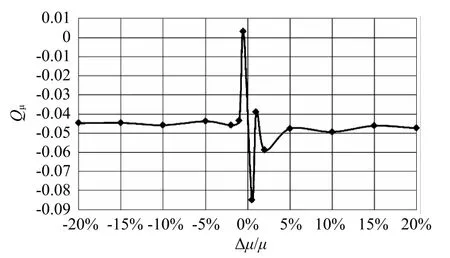
图2 Qμ随μ扰动的变化图

最后，对算例3进行计算。对μ进行扰动，相关指标值会发生变化，变化情况见表4、图3。

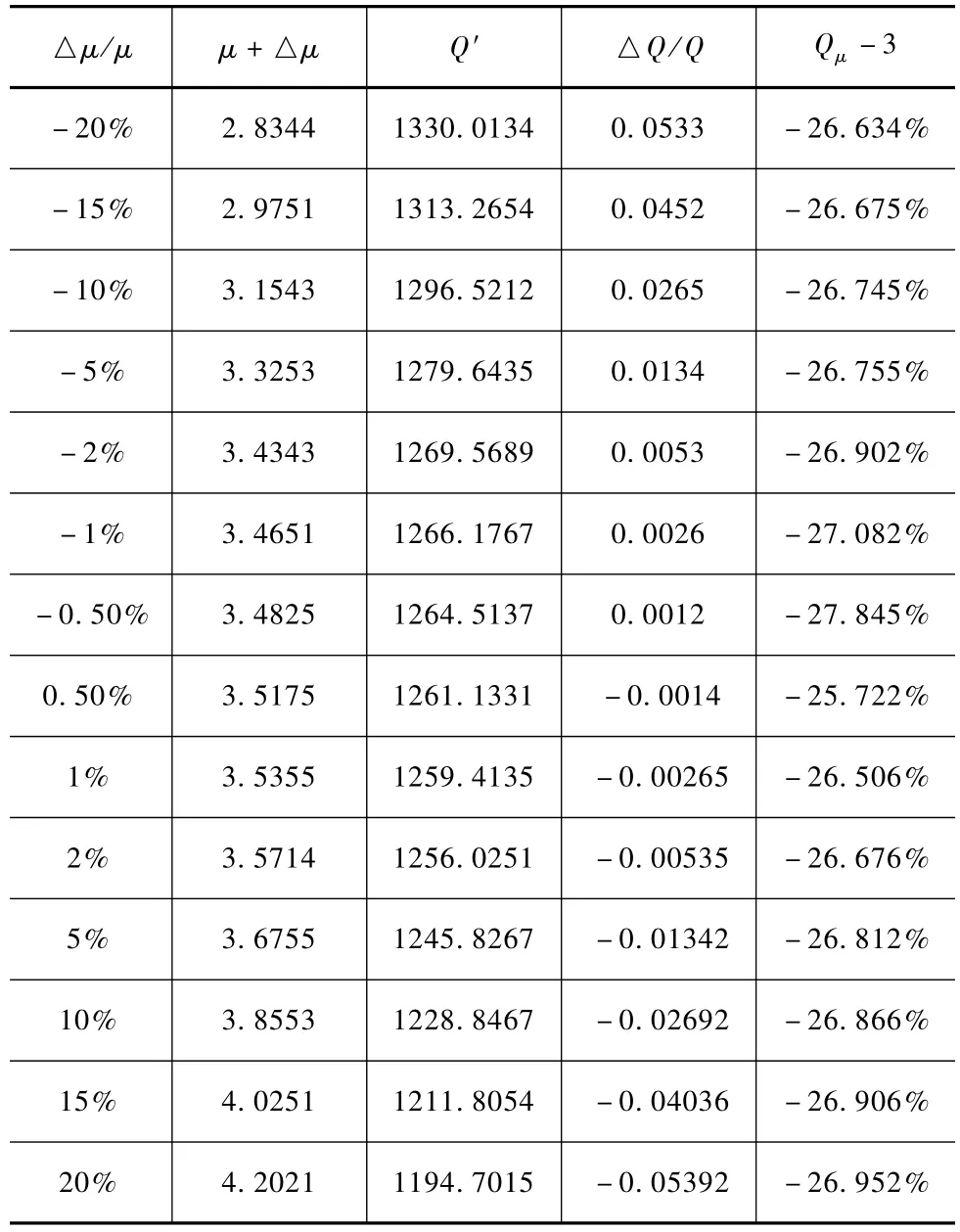
表4 Qμ随μ扰动的计算结果表

图3 Qμ随μ扰动的变化图

从以上3个算例的计算结果可知，损失参数变化对流域洪峰流量产生影响的灵敏度如下：（1）当Qμ的浮动范围为 ±20%时，Qμ值分布在区间［-0.28，0.01］上，其均值为0.1355；Qμ参数的绝对值始终小于0.3，表明μ的灵敏度低于0.3。从这个角度来看，运用推理公式法对洪峰流量进行计算时，计算结果降低了损失参数 μ的误差；（2）在μ扰动的过程中，Qμ总体变化特征较为平稳，变化幅度低于0.1。从这个角度来看，损失参数变化几乎不会对Qμ产生影响。

2.2 汇流参数灵敏度分析

在计算汇流参数m的灵敏度时，需要根据如下公式进行。

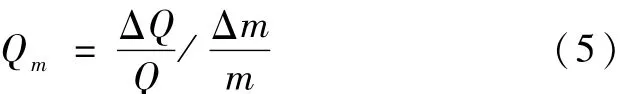
首先，算例1汇流参数m扰动结果见表5，数值变化情况如图4所示。

表5 Qm随m扰动的计算结果表

图4 Qm随m扰动的变化图

接着，对算例2进行计算，汇流参数m计算结果见表6，变化情况如图5所示。

表6 Qm随m扰动的计算结果表

图5 Qm随m扰动的变化图

最后，按照同样的方法对算例3进行计算，计算结果和变化情况分别见表7、图6。

表7 Qm随m扰动的计算结果表

图6 Qm随m扰动的变化图

从三个算例的计算结果可知：（1）当m的浮动范围为 ±20%时，Qm的变化区间为［0.81，1.19］，其均值为0.9933。从波动情况来看，Qm围绕1.0上下浮动，且偏离距离十分小。可见，运用推理公式法对汇流参数m进行计算时，既可能降低m误差，也可能增加其误差。然而，m的灵敏度要大于0.3，主要集中于1.0附近；（2）从计算结果变化图可知，Qm会随着m的增加而降低，反向变化趋势明显。

2.3 河道纵比降的灵敏度

在分析纵比降J时，需要依据如下公式进行：

首先，对算例1的J进行扰动，结果及数值变化情况分别见表8、图7。

表8 QJ随J扰动的计算结果表

图7 QJ随J扰动的变化图

接着，对算例2的J进行扰动，计算结果及变化情况分别见表9、图8。

表9 QJ随J扰动的计算结果表

图8 QJ随J扰动的变化图

从扰动结果可知：（1）J在 ±20%内扰动时，QJ在区间［0.25，0.43］上变化，其绝对值低于0.5，表明J的灵敏度低于0.5。可见，运用推理公式法对洪峰流量进行计算，能够降低J的误差；（2）QJ与J呈显著的反向变化趋势。

2.4 最大降雨量的灵敏度分析

在计算最大降雨量H24时，需要根据如下公式进行：

首先，对算例1进行最大降雨量扰动，扰动结果及变化情况分别见表10、图9。

表10 QH24h随H24扰动的计算结果表

图9 QH24h随 H24扰动的变化图

接着，对算例2进行H24h计算，计算结果及变化情况分别见表11、图10。

表11 QH24h随H24扰动的计算结果表

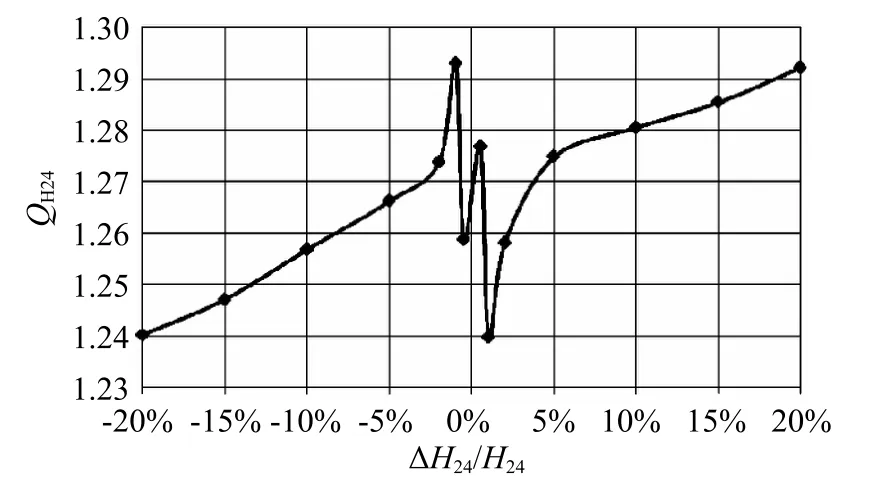
图10 QH24h随H24扰动的变化图

从以上2个算例可知：当H24的浮动范围为±20%时，QH24在区间［1.23，1.60］上变化，其绝对值要大于1.0，这表明 H24的灵敏度高于 1.0。可见，运用推理公式法对洪峰流量进行计算时，能够放大最大降雨量的误差。QH24与H24同向增大。

3 结语

通常情形下，损失参数μ的灵敏度低于0，洪峰流量Q与损失参数μ之间呈负相关，对Q的计算误差有缩小效用；通常情形下，河道纵比降J、汇流参数m以及24h内最大降雨量H24的灵敏度都为正，三者与洪峰流量Q的变化呈正相关，对Q的误差有放大效用；当J、m、μ以及H24的变化幅度为±5%时，所对应的参数灵敏度呈现较大波动。

［1］晁锐，郭建青，冯晓旭，等.推理公式法计算参数的不确定性与灵敏度分析［J］.人民珠江，2015（04）：29-31.

［2］汪集旸，陈建生，陆宝宏，等.同位素水文学的若干回顾与展望［J］.河海大学学报（自然科学版），2015（05）：406-413.

［3］周斌，赵正鹏.广西暴雨洪水计算的局部优化探讨［J］.人民珠江，2015（05）：55-57.

［4］陈哲.基于可靠性的城镇防洪水力计算的研究［D］.西南交通大学，2009.

［5］李立.浅析无资料小流域设计洪水计算——以乌兰察布高原东南部丘陵区为例［J］.水利规划与设计，2016（08）：50-52+76.

［6］石炜，徐永波，陈娟，等.华东地区小流域设计洪水计算方法探讨［J］.水利规划与设计，2015（12）：29-31.

［7］梁宏智.隆德县好水川河小流域坝系工程建设刍议［J］.水利技术监督，2014（05）：21-22+47.

［8］付默菡.锦凌水库库区小流域治理总体布置与措施设计分析［J］.水利技术监督，2015（04）：72-74.

TV122

A

1008-1305（2017）05-0083-06

10.3969/j.issn.1008-1305.2017.05.027

2016-08-31

艾力江·克力木（1973年—），男，工程师。