一种双惯性轮空间倒立摆及其动力学建模和分析

，， ， ，

(1.北京工业大学 信息学部，北京 100124； 2.计算智能与智能系统北京市重点实验室，北京 100124)

一种双惯性轮空间倒立摆及其动力学建模和分析

陈志刚1, 2，阮晓钢1, 2，李元1, 2，林佳1, 2，朱晓庆1, 2

(1.北京工业大学信息学部，北京100124； 2.计算智能与智能系统北京市重点实验室，北京100124)

针对现有的惯性轮倒立摆在模拟多自由度不稳定系统的局限性,提出了一种双惯性轮空间倒立摆系统，其具有四个自由度和两个控制量，可同时模拟不稳定系统俯仰和滚转姿态控制；运用拉格朗日方法建立了双惯性轮空间倒立摆的动力学模型，分别采用模型退化、数值仿真验证了所建立的模型的正确性，并分析了双惯性轮空间倒立摆的动力学特性；建立的双惯性轮空间倒立摆可应用于多自由度非平稳系统的模拟实验，提出的物理结构、模型和相关分析结论为双惯性轮空间倒立摆系统的进一步研究奠定了理论基础。

倒立摆；动力学模型；拉格朗日方程；惯性轮；反作用轮

0 引言

倒立摆控制系统作为典型的复杂、不稳定和欠驱动系统，广泛应用于科学研究[1-5]，是模拟非平稳系统的重要实验装置，尤其可应用于包括火箭、垂直起降飞行器和飞船等航空航天系统姿态控制的模拟验证中。倒立摆按结构形式分为直线倒立摆[6-8]、环形倒立摆[9-11]、平面倒立摆[12]和惯性轮(反作用轮)倒立摆[13-16]等。惯性倒立摆最先由Spong等提出[13,16]，由绕平面旋转的摆杆和布置在摆杆末端的惯性轮组成。在各种倒立摆装置中，惯性轮倒立摆具有简洁的动力学模型，更方便在研究中的推广。另外，基于系统的非线性和欠驱动特性，惯性轮倒立摆适合用于非线性控制的高级控制策略的研究。

近几年，惯性轮倒立摆受到了很多学者的关注[13-19]。Spong等[13-15]对惯性轮倒立摆的动力学建模和非线性控制进行了研究，对惯性轮倒立摆起摆和平衡控制策略进行了讨论。ALONSO等[17]对惯性轮倒立摆建模和参数辨识进行了研究，并建立了包含死区效应和黏性摩擦的摩擦模型。Olivares等[18]针对惯性轮倒立摆的非线性系统，设计了线性控制器。孙宁等[19]对惯性轮倒立摆的镇定控制问题进行了研究，提出了一种无需切换的滑膜鲁棒控制策略。

在垂直起降飞行器、飞船等航空航天器等不稳定系统的姿态调节中，系统做绕机体中心的俯仰和滚转运动，该类系统可等效为一个支点固定，摆杆可绕支点做纵向和横向摆动的倒立摆系统。在现有的倒立摆中，惯性轮倒立摆与此类不稳定系统具有更为相近的运动特性。现有的惯性轮倒立摆物理模型[13-19]中，摆杆只能在一个平面内摆动，摆杆只有一个回转自由度，属于二维模型，可模拟此类不稳定系统的单个运动方向的运动特性，这对模拟多自由度非平稳系统的控制(如火箭、垂直起降飞行器的姿态控制和人形机器人的平衡控制等)有较大的局限性[15-16,20]。

通过增加惯性轮倒立摆的摆杆自由度，可解决惯性轮倒立摆平衡控制与多自由度非平稳系统控制的模型等效问题，可更好的模拟此类多自由度非平稳系统的运动特性和多自由间的耦合特性[4,12]。本文构造了一种四自由度双惯性轮空间倒立摆系统，首先给出双惯性轮空间倒立摆的物理结构；然后，采用拉格朗日方程方法建立了其动力学模型；最后，分别运用了退化验证和数值仿真方法对模型进行了验证，分析了其动力学特性，并给出了本文研究的一些结论。

1 体系结构设计

本文所设计的双惯性轮空间倒立摆由可绕两个方向旋转的摆杆和布置在摆杆末端的可产生两个方向控制力矩的惯性轮构成，结构如图1所示。摆杆与支撑座间采用球销副联接，摆杆可以分别绕纵向和横向方向转动；反作用轮通过电机直接驱动，两组反作用轮在空间上相互正交，可提供纵向和横向的控制力矩；为平衡惯性轮组件的重量分布，分别在与反作用轮相对称的方位处设置有位置可调的配重块，通过调节配重块的位置，使得系统重心与摆杆轴线重合，降低系统重心偏移产生的干扰。

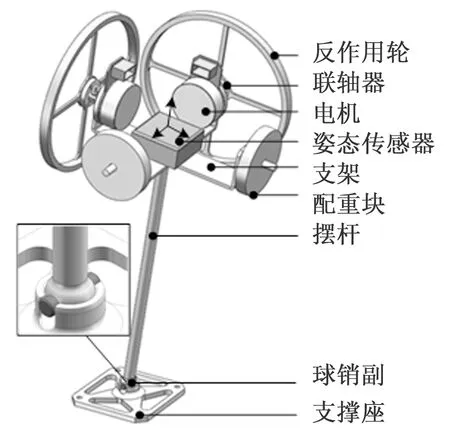
图1 双惯性轮空间倒立摆结构图

本文所构建的倒立摆电路结构示意图如图2所示，姿态传感器布置在摆杆上端，可检测摆杆分别绕横向和纵向偏转的角位置和角加速度；微处理器分别从姿态传感器读取摆杆的姿态角和角加速度、从编码器读取电机的转速，经运算后，通过伺服驱动器驱动两个电机回转，进而带动反作用轮回转产生惯性力矩控制双惯性轮空间倒立摆的姿态平衡。

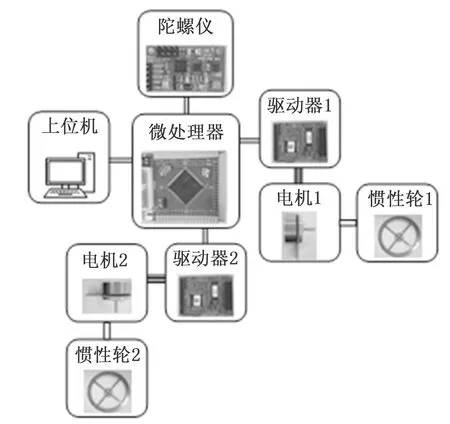
图2 双惯性轮空间倒立摆电器结构图

该双惯性轮空间倒立摆具有四个自由度和两个控制量，四个自由度分别为倒立摆绕横向的摆角、绕纵向的摆角、两个反作用轮的回转角，两个控制量为分别加载在两个电机上的电枢电压。双惯性轮空间倒立摆系统重心位于摆杆上端，属于欠驱动、非平稳系统。与普通惯性轮倒立摆相比，双惯性轮空间倒立摆具有更大的控制难度。双惯性轮空间倒立摆摆杆可指向三维空间内任意方向；在平衡控制中，与火箭、垂直起降飞行器等多自由度不稳定、欠驱动系统具有相似的运动特性，可应用于多自由度非平稳系统的模拟实验。

2 动力学模型

将双惯性轮倒立摆物理系统抽象为多刚体系统，运用拉格朗日方程建立系统的动力学模型。

2.1 参考坐标系定义

双惯性轮空间倒立摆以摆杆的下端回转点为支点，建立以摆杆下端回转点为原点的笛卡尔固定坐标系O-XYZ，如图3所示，其中：摆杆及电机定子的质心Cp到坐标原点O的距离、质量分别为lp、mp；单个惯性轮的质量为mw，惯性轮质心Cw到坐标原点O的距离为lw；摆杆相对于X轴、Y轴的转过角度分别为α、β；惯性轮分别相对于各自轴线转过的角度分别为θ、φ，摆杆和惯性轮相对其质心的转动惯量分别为Jp、Jw。

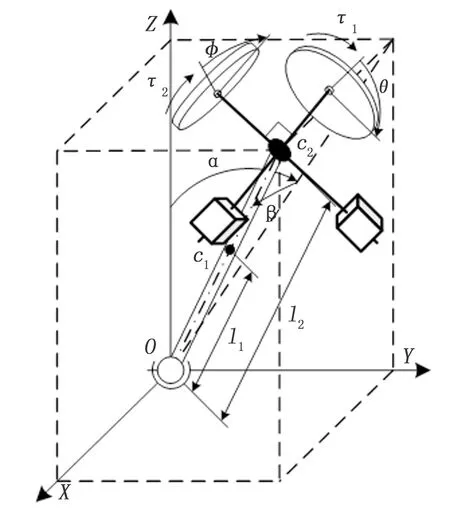
图3 双惯性轮空间倒立摆坐标系

假定摆杆与支撑座的摩擦力、惯性轮受到空气的阻尼力可忽略不计。根据几何关系可知，质心C1、C2在固定坐标系中的坐标为：

(1)

2.2 拉格朗日函数

利用拉格朗日方程方法建模，计算系统动能，其中摆杆的动能为:

(2)

惯性轮组件的动能为:

(3)

则系统的总动能为：

T=Tp+Tw=

(4)

式中,k1=Jp+ 2mwlw2；k2=mplp2+ 2mwlw2。

系统总势能为：

V=k3cosαcosβ

(5)

式中,k3=(mplp+2mwlw)g。

可得拉格朗日函数如下：

L=T-V=

k3cosαcosβ

(6)

2.3 动力学方程

取广义坐标为α、β、θ和φ，拉格朗日方程如下：

(7)

由于双惯性轮空间倒立摆的直流电机采用基于PWM电压控制方式，定义电机力矩常数为Kt，反电动势常数为Kb，电枢电阻为Rm，电枢电感为Lm，两个电机的电枢电压为分别v1、v2，根据直流电机的动力学模型：

(8)

输入力矩τ1,2=Kti1,2，忽略电机电感常数，可推导出电机的力矩方程为：

(9)

式中：a=Kt/Rm；b=Kt2/Rm。

将式(6)、(8)、(9)带入方程(7)中，可求解得系统动力学方程为：

3 模型的验证

由于建模过程中采用了多种近似条件假设，为检验所建模型的正确性，分别采用将模型退化验证和数值仿真系统的零输入响应的方法对模型进行验证。

3.1 退化验证

双惯性轮倒立摆与普通惯性轮倒立摆在结构上存在相似性。当固定双惯性轮倒立摆摆杆的横向或纵向的旋转自由度，双惯性轮倒立摆可转化为普通惯性轮倒立摆，退化后的双惯性轮倒立摆模型应与普通惯性轮倒立摆模型一致。

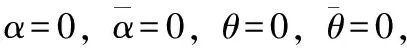
(11)

(12)

对比方程(11)、(12)，可见二者是一致的，退化后的双惯性轮空间倒立摆动力学模型与Spong等[13-15]建立的普通惯性轮倒立摆的模型一致，说明普通惯性轮倒立摆模型为双惯性轮空间倒立摆模型的特例，一定程度上说明本文所建立的双惯性轮空间倒立摆的模型及退化模型是正确的。

3.2 系统零输入响应

系统动力学模型如方程(10)所示，通过数值仿真系统的零输入响应对模型进行验证。假设对α、β角无限位，按照实际情况，两个电机的输入电压为零，除α外，系统其他初始状态均为零，空间倒立摆分别从不同的α0处开始运动，由于受到电机电磁力作用，系统运动中有能量损耗，摆杆应作绕X轴的减幅震荡，最终稳定在180°方位(即垂直向下)；在电磁力和科氏惯性力的共同作用下，与之对应的惯性轮应做微副摆动；摆杆相对于Y轴的回转角β及对应惯性轮的回转角φ应保持为零。系统物理参数如表1所示，α0分别为5°、90°、180°，系统零输入响应曲线如图4所示。

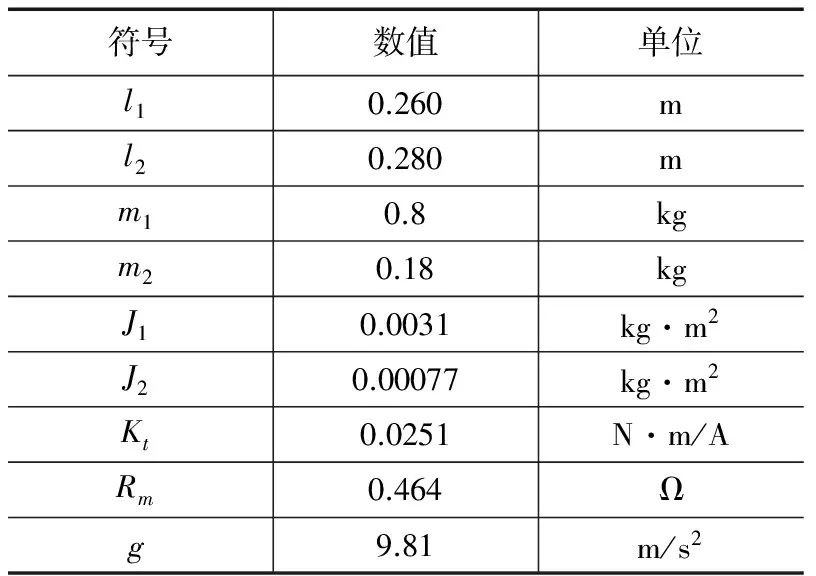
表1 双惯性轮空间倒立摆物理参数

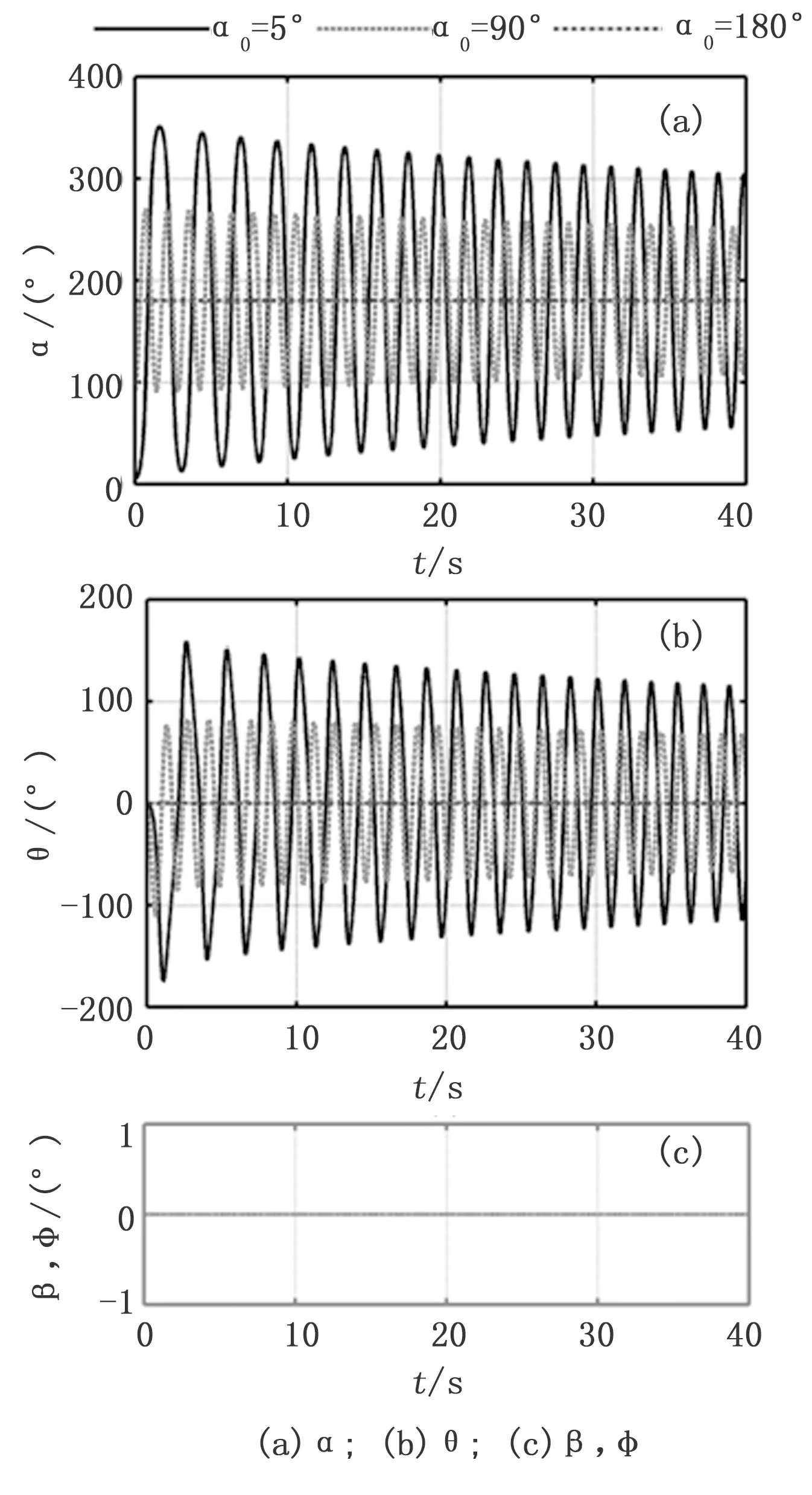
图4 不同α0时系统零输入响应

由图4可见，随时间的变化，摆杆摆角α0从5°开始在区间[5°,342°]内，关于180°的位置作减幅摆动，且摆杆的摆动角速度也呈减幅震荡，并趋向于零，所以摆杆趋向稳定与180°的位置(竖直向下)。当摆杆摆角从90°开始运动时，则α角在区间[90°,268°]内关于180°的位置作减幅摆动。在每个摆动周期中，受惯性力的作用，起始时，惯性轮产生与摆杆摆动方向相反的摆动，随着惯性轮及电机的转速增大，惯性轮及电机受到的电磁力阻力快速增大，使惯性轮减速；β、φ保持为零。

同理，输入电压及系统其他初始状态均为零，空间倒立摆分别从不同的β0开始运动，摆杆应做绕Y轴的减幅震荡，最终稳定在180°方位；对应的惯性轮应做微副摆动；摆杆相对于X轴的回转角α及对应惯性轮的回转角θ应保持为零。系统的零输入响应曲线如图5所示。可见，在不同的初始输入状态下，系统的零输入响应与实际情况一致，从而说明了此模型的正确性。

图5 不同β0时系统零输入响应

4 动力学分析

稳定性是系统的一个基本结构特征，稳定是控制系统能够正常运行的前提，能控性和能观性是从控制和观察的角度表征系统结构的基本特性[21]；重心高度和惯性轮转动惯量大小是系统的两个重要参数，对系统的动力学特性有着重要的影响，对上述参数的分析在系统控制律和结构设计中有重要的指导意义。

4.1 系统稳定性分析

(13)

其中：

采用李雅普诺夫第二方法判定系统稳定性，若系统是稳定系统，给定正定的实对称矩阵Q，且取为6维的单位阵，则存在正定的实对称矩阵P满足:

AT+PA=-Q

(14)

解得矩阵P，通过计算矩阵P的行列式可知其存在小于零的主子式，说明P不是正定矩阵，系统不是渐进稳定的[21]，即双惯性轮空间倒立摆在xe邻域内不是渐进稳定，在受扰动运动中，其无法自行维持平衡倒立姿态。

4.2 系统能控性和能观测性分析

双惯性轮空间倒立摆的运动性能指标一般要求控制摆角α、β在±10°内变化，所以在双惯性轮空间倒立摆的xe邻域内分析其能控性和能观测性。根据系统线性空间状态方程，分别构造系统能控性矩阵和能观测性矩阵:

(15)

4.3 重心高度分析

根据系统动力学方程(10)，令β=0，并带入k1、k2、k3、a、b后，得：

(16)

令α=0，得：

(17)

4.4 惯性轮转动惯量分析

根据系统动力学方程(12)，令α=0，β=0，得：

(18)

5 结论

1)本文提出的双惯性轮空间倒立摆属于自然不稳定、非线性、欠驱动系统，系统具有两个输入量，四个自由度。所建立的双惯性轮空间倒立摆模型的退化模型与普通惯性轮倒立摆模型一致，系统的零输入响应数值仿真结果与实际情况一致，验证了本文所建模型的正确性。

2)双惯性轮倒立摆系统在倒立平衡点非自治稳定和局部可控；同等质量下，系统重心越高，需要的控制力矩越大，控制周期也越大；同等质量下，惯性轮的转动惯量越大，需要的电机最大转速越小。

3)普通惯性轮倒立摆属于双惯性轮倒立摆的特例，双惯性轮空间倒立摆的动力学模型比普通惯性轮倒立摆更复杂，且存在耦合关系，对倒立摆的平衡控制策略提出了新的难度，如何设计双惯性轮空间倒立摆的平衡控制器成为进一步的研究内容。对于双惯性轮空间倒立摆控制的进一步研究也必将促进多自由度不稳定、欠驱动系统控制方法的拓展。

[1] Grasser F, D’Arrigo A, Colombi S, et al. JOE: A Mobile, Inverted Pendulum[J]. IEEE Transactions on Industrial Electronics, 2002,49(1): 107-114.

[2] 周 昆,孙明玮,陈增强. 快速显式预测控制在倒立摆系统中的应用[J]. 仪器仪表学报,2014, 35(9):2037-2044.

[3] 祁 虔,李祖枢,谭 智, 等. 模糊九点控制器及其在倒立摆系统中的应用[J]. 仪器仪表学报,2010, 31(6):1249-1254.

[4] 王家军, 刘栋良, 王宝军. X-Z倒立摆的一种饱和非线性稳定控制方法的研究[J]. 自动化学报, 2013, 39(1): 92-96.

[5] 刘 涵,周党伟,钱富才. 基于支持向量机模糊推理的二级倒立摆控制[J]. 仪器仪表学报,2008, 29(2):330-335.

[6] Brisillar M, Sankaranarayanan V. Nonlinear control of mobile inverted pendulum[J]. Robotics and Autonomous Systems, 2015, 70: 145-155.

[7] 张永立. 空间多级倒立摆非线性控制方法研究[D]. 大连: 大连理工大学, 2011.

[8] Kin S, Kwon S J. Dynamic modeling of a two-wheeled inverted pendulum balancing mobile robot[J]. Int.J.Control Autom. Syst, 2015, 13(4): 926-933.

[9] 刘浩梅,张昌凡. 基于LQR的环形单级倒立摆稳定控制及实现[J]. 中南大学学报(自然科学版), 2012, 43(9): 3496-3501.

[10] Liaow D, Liu Z B, Wen S J, et al. Fractional PID based stability control for a single link rotary inverted pendulum[C]. International Conference on Advanced Mechatronic Systems, 2015: 562-566.

[11] Casanova V, Alcaina J, Salt J, et al. Control of the rotary inverted pendulum through threshold-based communication[J]. ISA Transactions, 2016, 62: 357-366.

[12] Tang Y C, Zhou D Y, Jiang W. A New Fuzzy-Evidential Controller for Stabilization of the Planar Inverted Pendulum System[J]. PLOS ONE, 2016, 11(8): e0160416.

[13] Spong M W, Corke P, Lozano R. Nonlinear control of the Reaction Wheel Pendulum[J]. Automatica, 2001, 37(11): 1845-1851.

[14] Fantoni I, Lozano R, Spong M W. Stabilization of the Reaction Wheel Pendulum Using an Energy Approach[C]. Proceedings of European Control Conference,2001: 2552-2557.

[15] Block D J, Karl J A, Spong M W. The Reaction Wheel Pendulum[J]. Synthesis Lectures on Controls and Mechatronics, 2007, 1(1): 1-105.

[16] Olfatisaber R. Global stabilization of a flat underactuated system: the inertia wheel pendulum[A]. IEEE Conference on Decision & Control[C]. 2001, 4: 3764-3765.

[17] Alonso D, Robbio F, Paolini E, et al. Modelling an Inertia Wheel Pendulum Benchmark[J]. Mathematical and Computer Modelling of Dynamical Systems, 2005, 11(3): 255-272.

[18] Olivares M, Albertos P. Linear control of the flywheel inverted pendulum[J]. ISA Transactions, 2014, 53(5):1396-1403.

[19] 孙 宁, 方勇纯, 陈 鹤. 欠驱动惯性轮摆系统全局滑模控制[J]. 控制理论与应用, 2016, 33(5): 653-661.

[20] 赵 洪, 李建波, 崔 钊. 小型无人涵道飞行器飞行动力学特性[J]. 航空动力学报, 2014, 29(7): 1721-1728.

[21] 张嗣瀛，高立群. 现代系统理论[M]. 北京: 清华大学出版社, 2006: 107-181.

DoubleInertiaWheelSpatialInvertedPendulumandItsModelingandDynamicAnalysis

Chen Zhigang1，2, Ruan Xiaogang1，2, Li Yuan1，2, Lin Jia1，2, Zhu Xiaoqing1，2

(1.Faculty of Information Technology, Beijing University of Technology, Beijing 100124, China; 2.Beijing Key Laboratory of Computational Intelligence and Intelligent System, Beijing 100124, China)

Aiming at limitations of inertia wheel inverted pendulum in simulatingofmulti-freedom and unstable systems. A novel DIWSIPS(double inertia wheel spatial inverted pendulum system)was proposed, which have four freedom and two control variables. A DIWSIPS can be used in attitude control simulation both for pitch and roll simultaneousfor unstable systems. A dynamics model of DIWSIPS was derived from Lagrange equation. The correctness of the model was verified by model degradation and numerical simulation. And the dynamic characteristics of the DIWSIPS has been analyzed based on the dynamic model. The DIWSIPS can be used in simulation experiments of multi-degree of freedom unstable system. The proposed physical structure, dynamic model and analysis results provided theoretical basis for research of the DIWSIPS.

inverted pendulum；dynamics model；Lagrange equation；inertia wheel；reaction wheel

2017-06-22；

2017-08-18。

国家自然科学基金资助项目(61375086)；北京市自然科学基金项目/北京市教育委员会科技计划重点项目(KZ201610005010)。

陈志刚(1987-)，男，内蒙古人，博士研究生，主要从事自平衡机器人方向的研究。

1671-4598(2017)11-0257-05

10.16526/j.cnki.11-4762/tp.2017.11.065

TP273

A