混流式水轮机转轮设计变量耦合强度分析

朱国俊，罗兴锜，冯建军，卢金玲，吴广宽



混流式水轮机转轮设计变量耦合强度分析

朱国俊，罗兴锜※，冯建军，卢金玲，吴广宽

（西安理工大学水利水电学院，西安 710048）

在开展混流式水轮机转轮的多学科优化时通常需要进行设计变量的学科耦合强度分析，以便为建立简洁、高效的多学科优化求解策略提供依据。该文提出了一种基于全局相对灵敏度的转轮设计变量耦合强度分析方法，该方法基于参数化全三维反问题设计理论实现对转轮几何的参数化控制，并通过改进后的Morris OAT法进行各学科目标函数对转轮设计变量的全局相对灵敏度计算，然后以各设计变量的全局相对灵敏度集合为论域，引入模糊隶属度函数量化计算设计变量对各学科目标函数的隶属度。最后，以各设计变量的隶属度值为基础，提出了设计变量的耦合强度判定准则，为设计变量的耦合程度属性确定提供了参考。采用该文所提出的分析方法对某混流式水轮机模型转轮的设计变量开展了耦合强度分析，并根据变量的耦合强度分析结果开展了转轮的优化设计，优化后的转轮不仅使得水轮机在3个优化工况下的水力效率分别提高0.2%、0.82%和1.2%，同时叶片的空化和强度性能也得到改善，该结果表明该文所提出的混流式水轮机转轮设计变量耦合强度分析方法能可靠有效的界定各设计变量的耦合程度属性，从而验证了方法的可行性。

优化；设计；计算机仿真；混流式转轮；全局相对灵敏度；耦合强度分析；改进的Morris OAT 法

0 引 言

混流式水轮机转轮的优化设计方法由于受到传统的串行设计开发模式的桎梏，设计人员通常先针对转轮的流体力学性能开展优化设计[1-6]，然后再进行转轮的固体力学性能分析作为校核。这种方法曾经取得一定的成果，但随着如今国际水电市场的竞争环境越来越激烈，传统方法已难以兼顾水轮机多层次的有时甚至是矛盾的设计需求，该方法的一些弊端（如开发时间长、不同学科的设计人员对任务目标的评价标准有差异而导致设计工作搁置等等）也在设计过程中暴露。为消除传统方法中的弊端，转轮多学科优化设计方法逐渐获得设计人员的关注并应用于工程设计。

在混流式转轮的多学科优化设计过程中，多学科优化求解策略的具体结构决定了优化问题求解的复杂性及难度，而转轮设计变量的学科耦合强度属性则是确定优化求解策略具体结构的关键。目前国内外学者采用的分析设计变量耦合程度属性的方法有决策分析法[7]、基于聚类思想的方法[8-9]以及基于灵敏度分析的方法[10-11]等。在这些方法中，类似于决策分析法的新方法由于应用较少，其可靠性尚待研究；基于聚类思想的方法由于计算过程相对复杂，因此其应用缺乏普适性；而基于灵敏度分析的方法由于出现时间早[12]且理论计算过程简洁，所以获得了相对广泛的应用。但是，混流式转轮多学科优化问题中各设计变量的物理意义不尽相同，导致了目标函数对各设计变量的灵敏度存在量纲及量级上的差异，不利于对比分析。此外，在建立混流式转轮多学科优化求解策略时，所需的设计变量耦合强度属性的类别数通常少于设计变量数目，因此只依靠各设计变量的灵敏度属性难以准确界定设计变量的耦合强度。

为解决基于灵敏度信息判定转轮设计变量耦合强度属性时出现的问题，本文提出了一种实用的设计变量耦合强度分析方法开展混流式转轮多学科优化设计中的变量耦合强度分析。以混流式转轮的参数化全三维反问题设计方法为转轮几何控制策略，该方法首先通过改进原Morris OAT法中的抽样技术提升其计算效率，然后基于改进后的Morris OAT法计算获得各学科目标函数对转轮设计变量的全局相对灵敏度信息，最后以设计变量的全局相对灵敏度数据集合为论域，引入模糊隶属度函数计算获得设计变量对各学科目标函数的隶属度，并以此为基础建立耦合强度判定准则为混流式转轮设计变量的耦合强度属性判定提供参考。

1 参数化全三维反问题设计方法

本文以混流式转轮全三维有旋流动反问题设计方法为基础，引入贝塞尔曲线参数化技术控制全三维反问题设计所需的边界条件，形成了混流式转轮的几何控制策略。混流式转轮全三维反问题设计理论假设转轮内部的流动沿圆周方向呈周期性变化，因此其内部流场可采用周向平均流场与周期性脉动流场的叠加进行模拟。周向平均流场通过由周向平均相对流动流函数和置于叶片中面的源汇所产生的势函数构建流动控制方程进行求解，周期性脉动流场则通过引入周期性锯齿函数构建周期性脉动流动控制方程进行求解，具体的方程形式参见文献[13]。转轮叶片方程根据叶片表面相对速度与叶片表面法向量垂直的物理边界条件构建，并在柱坐标系下最终化简如式（1）。

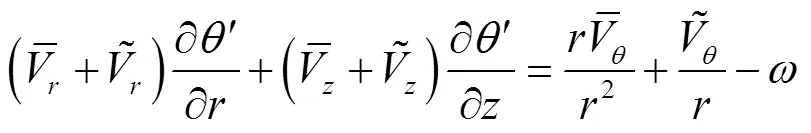
1.1 叶片区速度矩的参数化控制

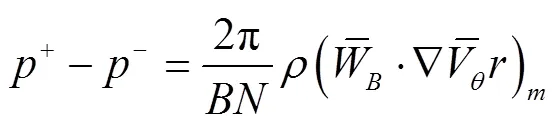
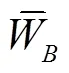
注：H和S分别为上冠、下环处速度矩控制点，=1,2,3,4。

Note:HandSare velocity momentcontrol point in hub and shroud,respectively,=1,2,3,4.

图1 速度矩参数化控制示意图

Fig.1 Schematic diagram of parameterized control of velocity moment

为了实现对叶片区速度矩分布的控制，如图1中所示，采用四阶三次贝塞尔曲线分别对上冠和下环处的速度矩分布实现参数化控制，上冠和下环间其余各轴面流线上的速度矩分布则根据线性分布插值获得。转轮叶片进口处速度矩只受导叶开度影响，所以在优化过程中保持不变。此外，为了保证机组运行的稳定性，维持转轮出口速度矩从上冠至下环等于0，因此转轮叶片区进口和出口处速度矩都固定不变，总结后即得速度矩控制点1、4、1、4不变。剩余可变化的控制点只有2、3、2、3，为了减少设计变量数目，只选择它们的纵坐标y2、y3、y2、y3作为控制变量，最终，叶片区速度矩控制变量数量为4个。

1.2 叶片轴面流道的参数化控制

转轮的轴面流道几何也是全三维反问题设计所需的边界条件，但是由于轴面流道中的下环几何型线的改变会导致标称直径1的变化，同时会使下环出口锥角与尾水管锥管尺寸不匹配，因此本文只将上冠型线的几何作为优化设计的对象，通过控制转轮上冠型线的形状可以改善叶片的空化性能以及调节转轮的过流能力。上冠型线是直接参与加工制造的关键几何形状之一，本文采用五阶贝塞尔曲线对其开展参数化控制，如图2所示。从图2可知，1～5是转轮上冠型线的贝塞尔控制顶点。为了保证转轮上冠与活动导叶流道的光滑连接，优化过程中保持控制点1坐标不变，同时只允许改变控制点2横坐标x2。叶片出口过流断面的面积是影响转轮过流量和叶片空化性能的关键因素，因此控制点4的横坐标x4也被选择为优化变量之一。除此之外，根据精简优化变量的原则，保持控制点3和5不变，则最终的上冠型线控制变量只有x2、x4。

注：P1~P5是转轮上冠型线的贝塞尔控制顶点。

1.3 叶片厚度分布的参数化控制

转轮叶片的厚度分布规律对叶片流体力学性能和强度性能都有直接影响，三维叶片的厚度分布规律主要由各流面上的翼型厚度分布规律组合形成，因此可通过控制各流面上的翼型厚度分布实现对其控制。流面上的翼型厚度分布规律可分解为最大厚度值和相对厚度分布规律两部分，为确保最终三维叶片的正背面光滑，各流面翼型的最大厚度值从上冠到下环按线性进行分布[14]，同时参考相近水头段优秀转轮叶片的最大厚度值分布，确定上冠与下环处翼型最大厚度的关系如式（3）。

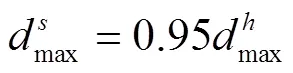
注：T为控制点，=1,2,3,4。

Note:Tiscontrol point,=1,2,3,4.

图3 翼型相对厚度控制示意图

Fig.3 Schematic diagram of foil's relative thickness controlled

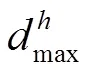
综上所述，混流式转轮叶片的参数化控制策略所需的设计变量参数集合如式（4）。

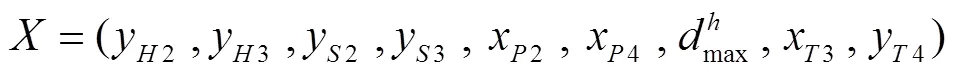
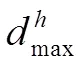
上述变量参数集合中的9个变量涵盖了叶片区载荷控制参数、转轮轴面流道控制参数以及叶片厚度控制参数，基本实现了对整个转轮几何的掌控。

2 目标函数选取及计算方法

转轮优化设计问题的主要目标是获取一个具有良好能量、空化及强度性能的转轮。为了考虑转轮与上下游过流部件的匹配性能，转轮的能量性能采用水轮机的水力效率作为衡量指标。转轮的空化性能采用转轮叶片上的最低压力系数min作为衡量指标，而转轮叶片的强度性能则采用叶片上的最大等效静应力max作为指标。因此，本文中混流式转轮的多学科优化目标函数集合为

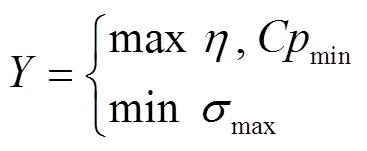
式中水力效率和最低压力系数min为无量纲数，max为最大等效静应力，MPa。

上述目标函数全部通过数值计算方法获取。水力效率和叶片表面最低压力系数通过采用CFX对水轮机进行全三维黏性数值计算获得，叶片最大等效静应力则通过ANSYS有限元分析计算获取。

3 基于改进Morris OAT法全局灵敏度分析

对设计变量参数集合中各设计变量开展耦合强度分析的前提是获得各设计变量的全局灵敏度信息。常用的全局灵敏度计算方法有：Sobol法[19]、傅里叶灵敏度计算法[20]、多元回归分析法[21]以及Morris OAT法[22-23]。Sobol法和傅里叶灵敏度计算法的计算公式复杂，在实际工程中应用较少。多元回归法和Morris OAT法都是基于全局抽样的分析法，其分析计算过程简便所以应用更为广泛，而两者中Morris OAT法以其计算量少的优势又更胜一筹，所以本文采用其作为全局灵敏度计算（global sensitive analysis, GSA）的方法。

常规Morris OAT法中的抽样技术是传统拉丁超立方抽样法，该方法存在所抽取的样本点在设计空间内分布不均匀的缺点，因此通常需要开展3～4次重复抽样计算以确保抽样点在设计空间内分布的均匀性，极大的增加了全局灵敏度分析的计算量。为了改进该方法的缺陷，本文引入优化拉丁超立方抽样技术替代Morris OAT法中的抽样方法。优化拉丁超立方技术是以中心离差度量最小为准则开展设计空间样本点抽取的试验设计方法[24]，其抽取的样本点在设计空间内分布均匀且确保每个样本的每个水平都被覆盖。采用该抽样技术与Morris OAT法相结合开展全局灵敏度计算时，只需进行一次样本点抽取和灵敏度计算即可。通过抽样技术获取所有的设计样本点后，根据以下方法开展各设计变量的全局相对灵敏度计算。

假如设计变量参数集合的维数为，全局灵敏度计算所需抽取的样本点总数为，则对于个设计样本点中的某个样本点X，其表达式如下

X=(x1,x2,…,x,…,x) （6）

式中x代表设计变量参数集合中的第个设计变量x在样本点X处的取值，=1, 2, …,，=1, 2, …,。

则根据Morris OAT法可知[25-26]：在样本点X处，目标函数()对设计变量参数集合中的第个变量x的相对灵敏度为

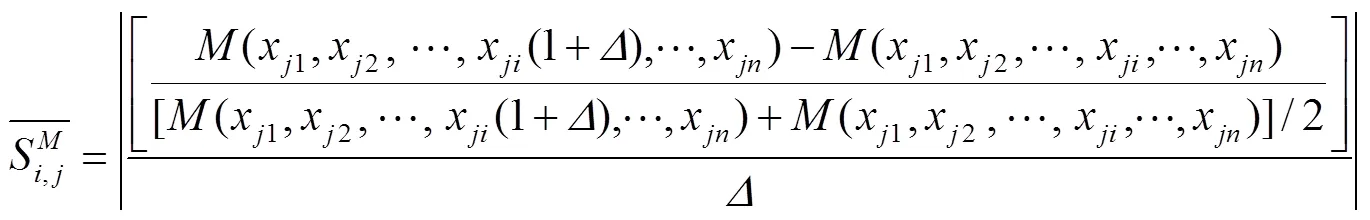
式中(…)为目标函数值，为设计变量x在样本点X处的扰动，=1, 2, …,，=1, 2, …,。样本点X在全局灵敏度的计算过程中也被称为基值点。根据文献[27]，式（7）中各设计变量的扰动可取为5%，然后可通过式（7）计算获得x在所有抽样点处的相对灵敏度。最后，根据Morris OAT法，依据式（8）计算x的全局相对灵敏度。

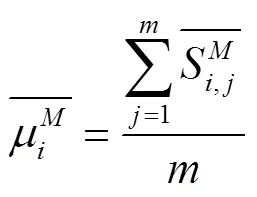
4 耦合强弱程度判定准则的建立

设计变量的耦合强弱程度由其对各学科目标函数的影响程度大小体现。同时对各个学科的目标函数影响程度大的变量即为强耦合变量，只对其中某个学科的目标函数有影响，而对其他学科目标函数影响程度很小或没有影响的变量为弱耦合变量，由此可见，设计变量耦合程度的“强”和“弱”是一个模糊概念。为了对其进行定量划分，本文引入模糊数学中隶属度函数的概念，以各设计变量的全局相对灵敏度数值为基础，通过归一化计算获得设计变量对目标函数的隶属度，如此即可在统一的量化标准下制定设计变量的强弱耦合程度判定准则。

在本文所关注的3个目标函数中，水力效率和最低压力系数min为流体力学学科的目标函数，而叶片的最大等效静应力max则为固体力学学科的目标函数。各目标函数对设计变量的全局相对灵敏度可写成式（9）所示的集合模式。

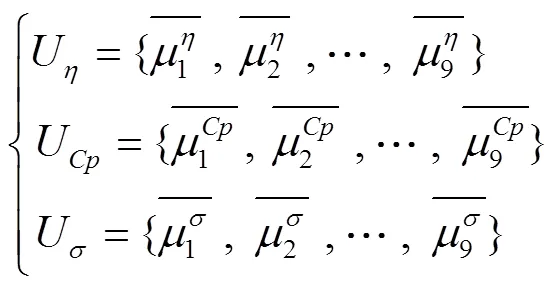
将各目标函数的全局相对灵敏度集合U、U、U分别作为论域，定义“对目标函数影响程度大的设计变量”为论域上的模糊集，则通过该模糊集的隶属度函数即可完成论域中各元素对模糊集的隶属度确定，从而实现论域到隶属度集合的变换。

不同的研究人员会根据自身的习惯和偏好建立或选择不同型式的隶属度函数，尽管隶属度函数在型式上有区别，但在反映、解决实际模糊问题时殊途同归。本文中的模糊集定义是“对目标函数影响程度大的设计变量”，属于寻找论域中“偏大型”元素的模糊问题，因此本文选择了半梯形分布的偏大型函数()作为隶属度函数。

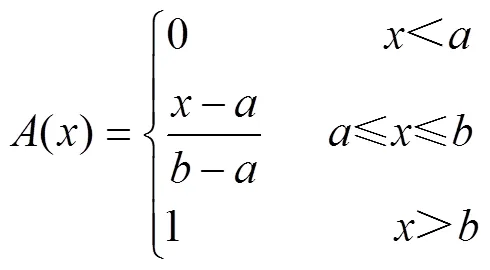
式中取所研究论域中的最小值，取所研究论域中的最大值。通过式（9）和（10），设计变量对各目标函数的隶属度被统一映射到[0,1]的数值区间，并可写成如下形式。

A={a1,a2,…,a9}

A={a1,a2,…,a9} （11）

A={a1,a2,…,a9}

式中a、a、a分别表示设计变量对水力效率、最低压力系数min以及叶片上最大等效静应力max的隶属度值，=1, 2, …, 9。

在获得每个设计变量对各目标函数的隶属度以后，为了使设计变量的耦合强度分类更为合理，本文根据设计变量的隶属度数值将设计变量的耦合强度分为强耦合、中等耦合和弱耦合3种。对于设计变量参数集中的任意一个设计变量，本文将其耦合强度属性分类的原则定义如下：

1）若设计变量对各个学科目标函数的隶属度数值都为1，则该设计变量为强耦合设计变量。

2）若设计变量对各个学科目标函数的隶属度函数值都属于（0,1）的数值区间，或只对其中某个学科目标函数的隶属度函数值为1而对其他学科目标函数的隶属度函数值属于（0,1）的数值区间，则称该设计变量为中等耦合设计变量。

3）若设计变量只对某个学科目标函数的隶属度函数值不为0而对其他学科目标函数的隶属度函数值都为0，则表明该设计变量为弱耦合设计变量。

根据上述设计变量的耦合强度属性定义，对本文所研究的混流式转轮叶片的任一设计变量，可制定其耦合强度判定的隶属度取值原则如表1所示。

表1 设计变量耦合强度判定的隶属度取值原则

注：a、a、a分别代表任一设计变量对目标函数、min及max的隶属度。

Note:,aandarepresent the membership of the design variables to the objective functions,minandmaxrespectively.

针对混流式转轮叶片，综合式（11）中各目标函数隶属度集合中的数据及表1中的判定原则即可判定各设计变量的耦合强度属性，然后再根据设计变量集合中的强、弱耦合变量的数量即可确定多学科优化设计求解策略，为混流式转轮的多学科优化奠定基础。

5 应用算例

5.1 算例相关参数

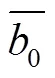
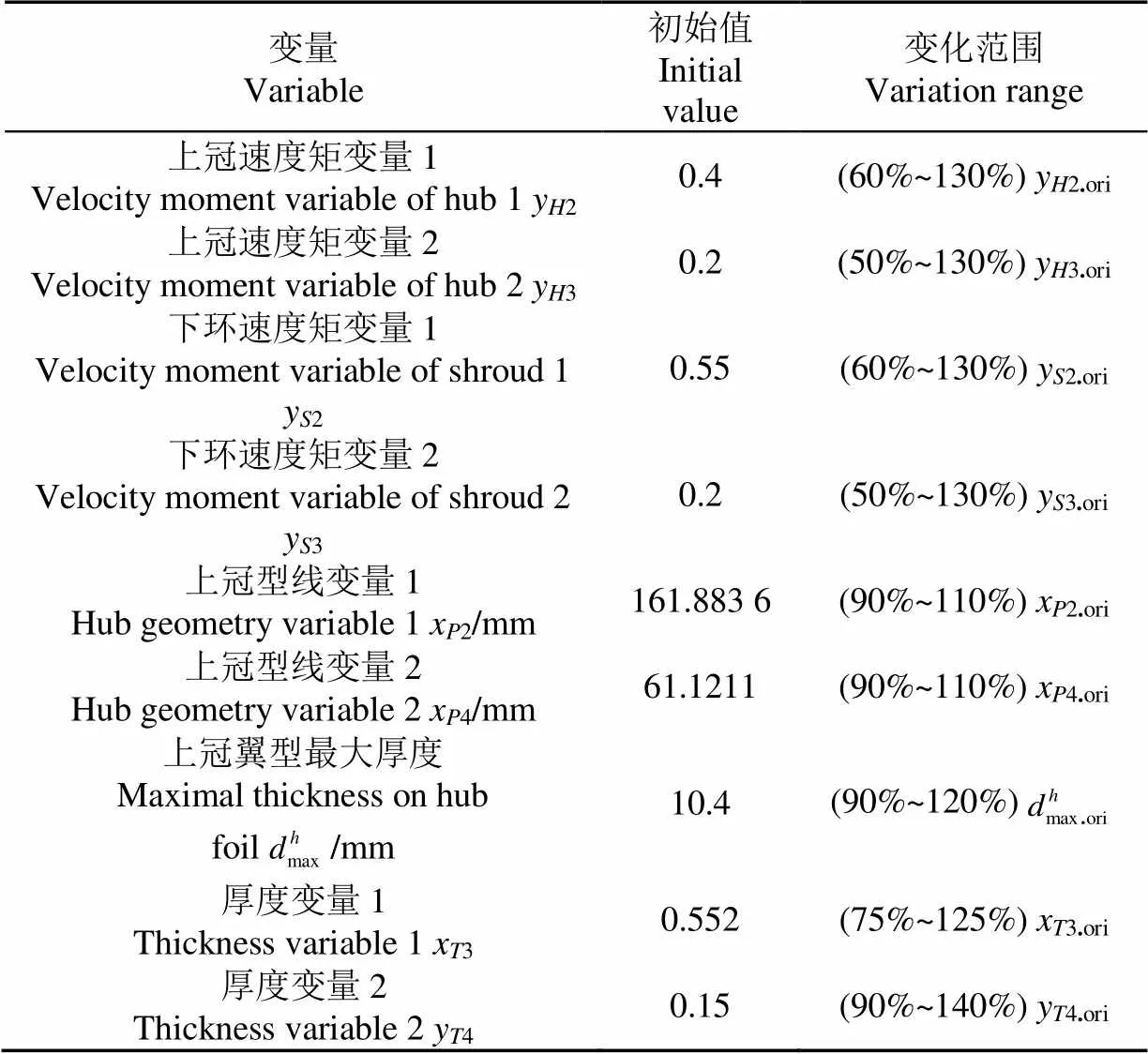
表2 设计变量初始值及变化范围

注：当变量下标中含有.ori时，表示其为对应变量的初始值。

Note: The variable which subscript contains .ori represents the initial value of corresponding variable.

确定设计变量的变化范围后，选取每个设计变量的变化水平数为10，并使水平取值在各变量的变化范围内均布，然后将每个设计变量的10个水平取值分别以1～10的整数进行编码，则根据优化拉丁超立方抽样方法可以产生10个基值点的水平取值矩阵，在确定了基值点以后即可按照本文第3节所述方法开展各设计变量的全局相对灵敏度计算。

5.2 目标函数的计算方法

在相对灵敏度计算过程中，各基值点对应的目标函数值以及设计变量发生扰动后的目标函数值全部通过数值计算方法获取，根据Morris OAT法的计算原理，总共需要开展数值分析的次数为：基值点数×设计变量数=90。

水力效率和最低压力系数min为流体力学学科的目标函数，本文拟通过对水轮机内部流动进行流体动力学分析获得其数值。尽管目前的计算机运算速度已经获得了巨大提升，但是开展90次混流式水轮机全流道计算仍然具有很大的计算工作量，因此，出于减少灵敏度分析过程中计算工作量的目的，本文选择了单周期的活动导叶、转轮与尾水管作为流体动力学计算域开展数值分析，采用六面体结构化网格离散的计算域如图4所示。

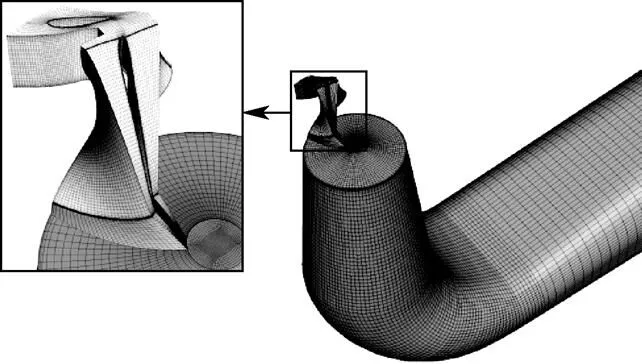
图4 流体力学计算域

由于目标函数对设计变量的敏感度实质是目标函数对转轮几何形状的敏感度，而转轮几何变化对水轮机性能的影响主要体现在2点：第一，转轮几何变化对其自身性能的改变；第二，转轮几何变化对下游尾水管水力性能的影响，因此，选择图4所示计算域进行流体动力学分析足以反映目标函数对转轮设计变量的敏感度。图4所示计算域的进口为活动导叶进口，给定质量流量边界条件，方向为固定导叶出流方向。计算域出口为尾水管出口，给定静压边界条件。所有固壁面都采用无滑移壁面。计算域网格总数经过以水力效率为基准的无关性验证后确定为150万。湍流模型采用SST湍流模型，该模型结合Wilcox模型和模型的优点，并且对于逆压梯度引起的分离流动有较高的预测精度[28-29]。为了检验数值计算的可靠性，在最优单位转速11= 67.5 r/min时，选取了单位流量510、549、588 L/s 3个工况对原始转轮下该模型水轮机的性能进行了数值计算，将计算所得水力效率与试验值进行对比如图5所示，图5中的偏差为绝对偏差，其计算公式如式（12）所示。

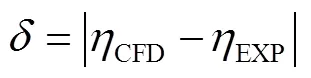
式中ηCFD为数值计算所得水力效率，ηEXP为模型试验的数据值。

从图5的数据对比中发现，尽管由于没考虑蜗壳、固定导叶的损失使得计算值偏高于试验值，但数值偏差小于2%，同时数值计算较好地反映了试验数据的趋势，因此采用本文数值计算方法分析转轮形状变化对水轮机流体力学性能目标函数的影响是可行的。另一个流体力学目标函数min则根据CFD计算结果以式（13）进行计算获得其数值。

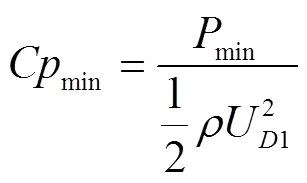
式中min为叶片上压力最低值，Pa；为流体密度，kg/m3；U1为转轮叶片进口标称直径1处的圆周速度，m/s。

固体力学目标函数max通过对叶片进行有限元分析获取。依据文献[30]中的研究结论，为了缩短整个灵敏度计算的时间周期及有限元计算工作量，可只选取叶片作为分析模型研究叶片的强度，因此本文只选取叶片实体域作为有限元分析对象。叶片实体域的计算载荷条件设置如下图6a中所示。

叶片首先需要考虑重力载荷，其次，叶片还受到旋转所引发的离心力作用，因此还需考虑旋转效应。叶片表面设置为流固耦合面，根据叶片的受力特点，叶片实体与上冠、下环的接触端设为固定约束条件。叶片实体采用solid185六面体单元进行离散，划分的叶片实体网格如图6b中所示，叶片实体网格节点总数为238 915。有限元计算中流固耦合面上各节点的水压力载荷按其对应的坐标位置在CFD计算结果中插值获得。计算完成后提取叶片上的最大等效应力作为固体力学的目标函数max。

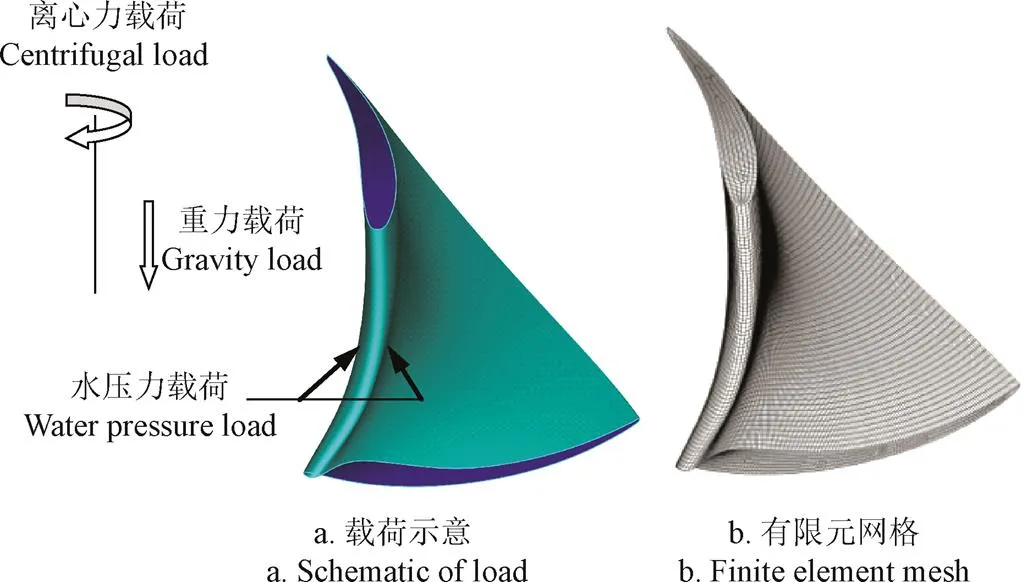
图6 载荷条件与有限元网格

5.3 耦合强度分析结果及有效性验证

在设计点工况下，根据上述目标函数计算方法对本文5.1节中的10个基值点以及各基值点处设计变量发生扰动后的目标函数值进行了计算，然后根据式（7）、（8）计算获得各目标函数对各设计变量的全局相对灵敏度如表3所示。

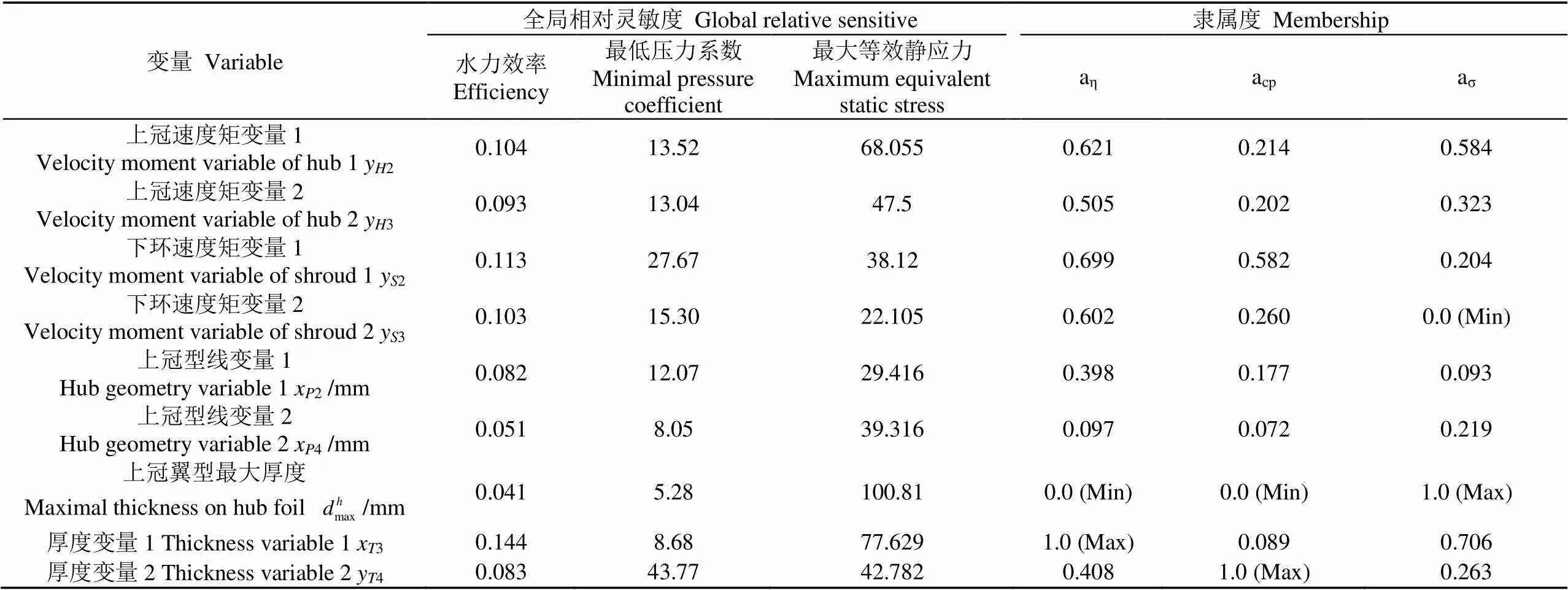
表3 设计变量的全局相对灵敏度和隶属度

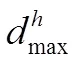
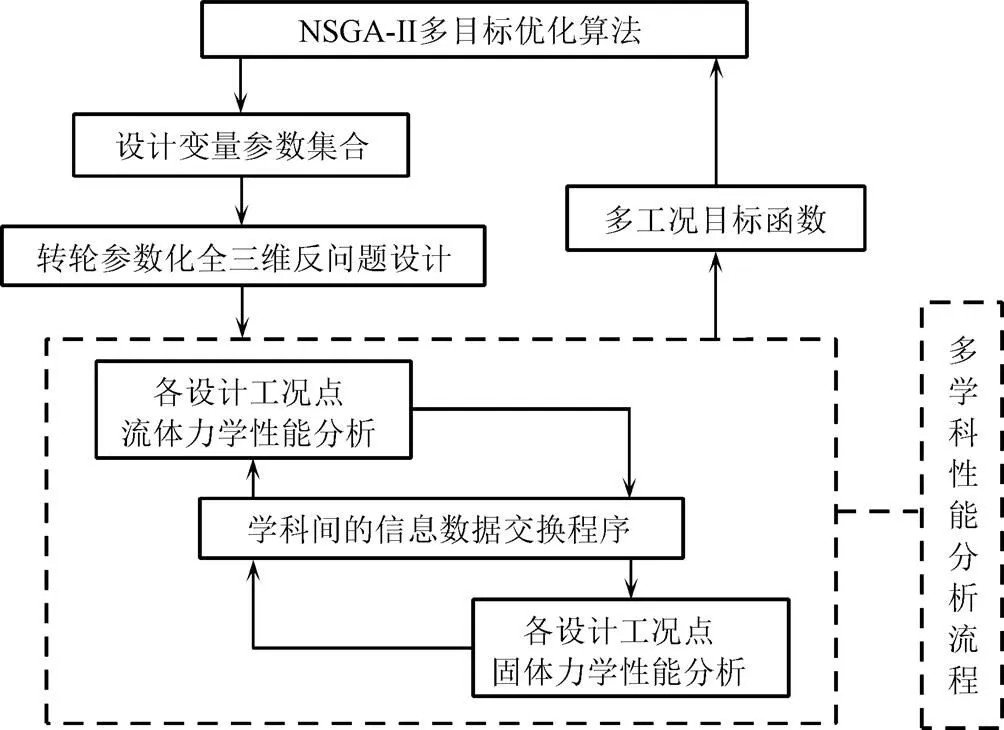
图7 多学科可行性求解策略结构

根据图7的优化求解策略建立具体的优化设计框架结构开展转轮的优化，优化工况点如表4。

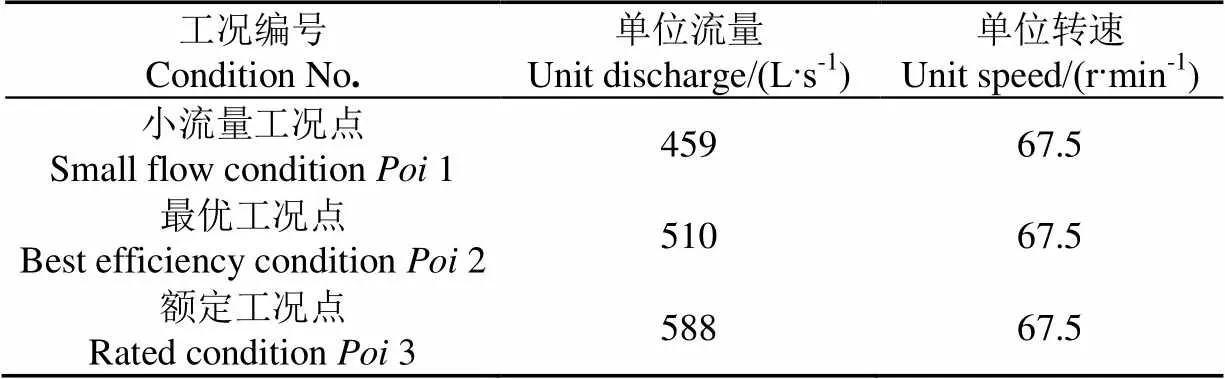
表4 优化工况点

每个工况包含、min和max3个目标函数，目标函数高达9个，使优化问题成为高维优化问题。为有效求解该优化问题，采用作者提出的嵌入设计者偏好的多工况优化设计方法对高维目标函数集合进行了降维处理。该方法通过引入设计者对各目标函数的期望将优化目标转变为：在满足所有约束条件下，寻求设计空间内的一个解，使其在优化工况下的性能与期望性能间的欧几里德距离最小。该方法的可行性和有效性已经获得验证[31]。采用该方法转换后的新目标函数如式（14）～（16）所示，目标函数由9个缩减为3个，优化问题的求解难度极大降低。

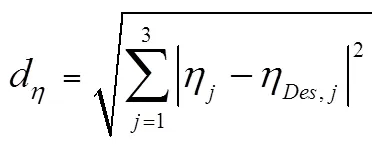
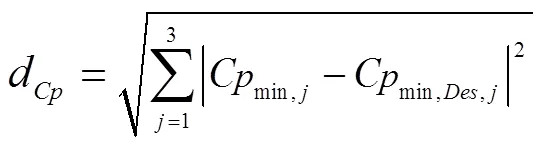
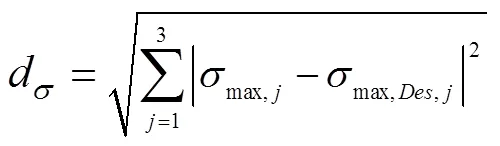
式中d、d和d为新的目标函数；η、min, j和max, j分别为工况下的3个目标函数值；η,j、min,Des,j和max,Des,j则为工况下3个目标函数的期望值，=1,2,3。

限于篇幅，下文只给出转轮的优化结果以验证本文方法的有效性。优化采用的NSGA-II算法的种群数为48，进化代数为35，交叉概率为0.8。优化求解在服务器上完成，优化过程中的种群在各二维目标函数平面内的投影如图8所示。

从计算所得的Pareto解中选取了性能提升较为均衡的解作为优化解，优化前后的几何对比如图9所示。

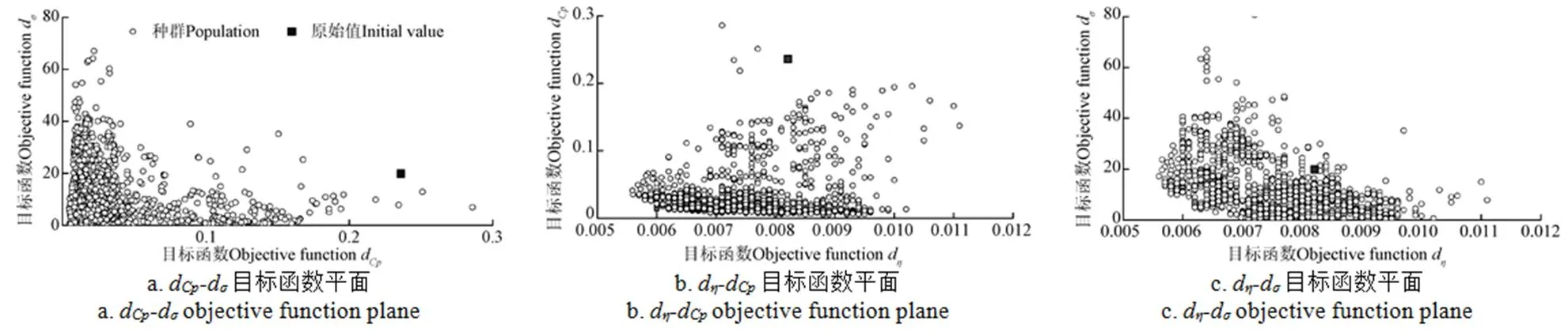
图8 优化中的种群分布

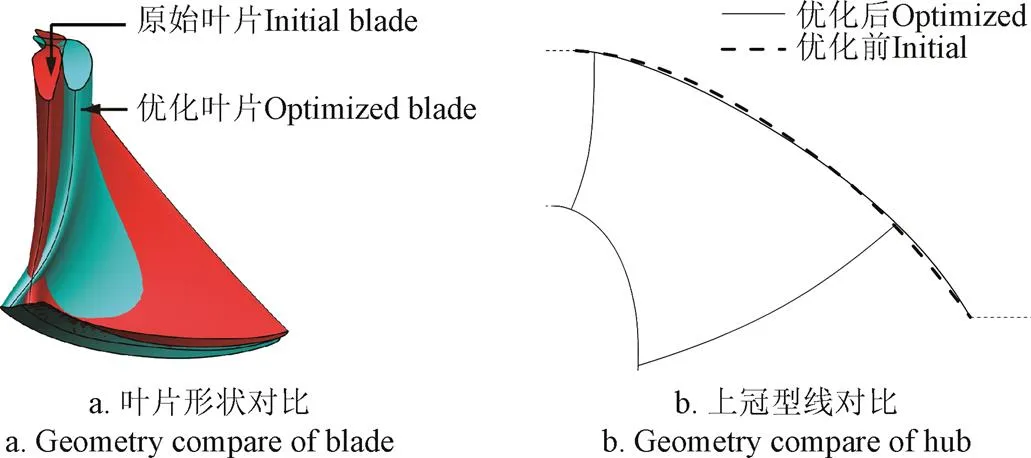
图9 叶片优化前后的几何对比

采用数值计算方法对优化前后的转轮开展全流道性能对比，网格采用经无关性验证后总数为654万的六面体结构化网格，湍流模型采用SST，蜗壳进口边界条件给定质量流量，尾水管出口边界条件给定静压，计算后的性能对比如图10所示。

图10a中给出了转轮优化前后的水轮机效率、转轮叶片上的最低压力系数的对比，图10b则给出了转轮叶片强度性能的对比。综合上述对比结果可知，对于优化的3个工况，机组的水力效率分别提升了0.2%、0.82%和1.2%，同时，转轮叶片的空化性能和强度也获得提升，说明转轮的流体力学和固体力学性能获得了较为全面的改善。优化结果证明了根据耦合强度分析结果选择的优化求解策略的可行性和有效性，也验证了本文所提出的耦合强度分析方法是有效的。

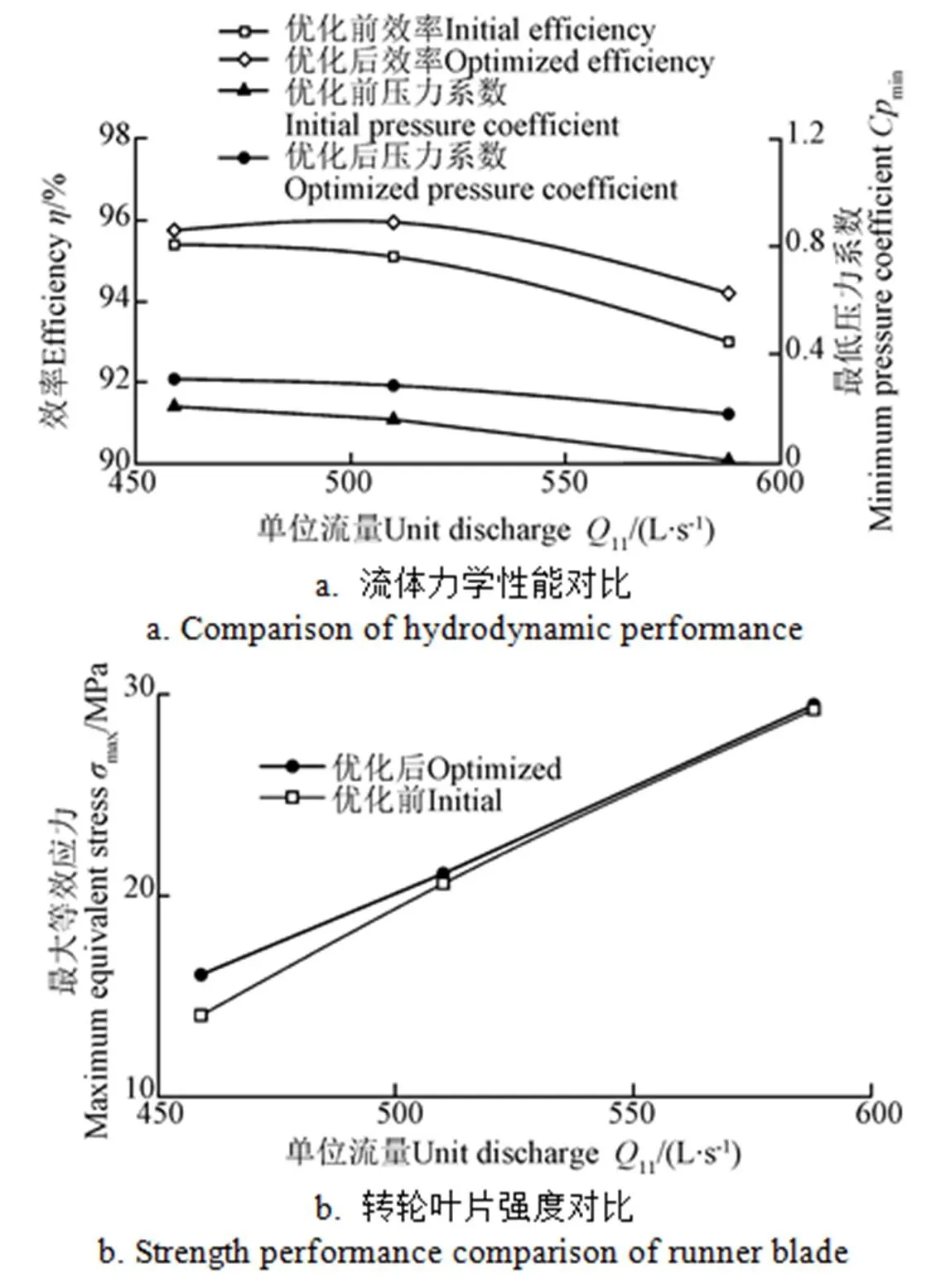
图10 优化前后的水轮机性能对比

6 结 论

1）本文提出了综合最优拉丁超立方抽样技术与Morris OAT法的全局相对灵敏度分析方法，通过该方法在混流式转轮设计变量灵敏度分析中的应用表明，其只需进行一次基值点的抽样计算。与传统Morris OAT法至少需要进行2～3次抽样计算相比，计算工作量减少了50%以上。

2）建立了一种判定混流式转轮设计变量耦合强度的方法，并应用该方法对某混流式模型转轮的设计变量开展了耦合强度分析。结果表明，在该混流式模型转轮的优化设计变量中，除了最大厚度值为弱耦合变量以外，其余变量均为中等耦合变量。同时，分析结果也表明本文所提出的耦合强度分析方法具备可行性。

3）根据耦合强度分析结果选择了综合计算成本低的多学科优化策略开展某混流式模型转轮的优化，最终结果表明优化设计不仅使得水轮机的水力效率在3个优化工况下分别提高了0.2%、0.82%和1.2%，还改善了转轮叶片的空化、强度性能，证明了所选择的优化求解策略的可行性，也验证了本文所提出的耦合强度分析方法是有效的。

[1] Vishnu Prasad, Gahlot V K, Krishnamachar P. CFD approach for design optimization and validation for axial flow hydraulic turbine[J]. Indian Journal of Engineering and Materials Sciences, 2009, 16(4): 229－236.

[2] Derakhshan S H, Mostafavi A. Optimization of GAMM francis turbine runner[J]. World Academy of Science- Engineering and Technology, 2011(59): 717－723.

[3] Priyono Sutikno. Numerical simulation of the Francis Turbine and CAD used to Optimized the Runner Design[C]// The 10thAsian International Conference on Fluid Machinery, Malaysia, 2010: 816－825.

[4] Suthep Kaewnai, Somchai Wongwises. Improvement of the runner design of francis turbine using computational fluid dynamics[J]. American Journal of Engineering and Applied Science, 2011, 4(4): 540－547.

[5] 刘敏，周大庆，吴国颖，等. 超低水头轴流式水轮机CFD优化及流动特性研究[J]. 水电能源科学，2016(1)：150－153.

Liu Min, Zhou Daqing, Wu Guoying, et al. CFD optimization and study of flow characteristics of axial flow turbine with ultra-low head[J]. Water Resources and Power, 2016(1): 150－153. (in Chinese with English abstract)

[6] 孙见波，李颖，徐伟，等. 基于CFD和FEM的混流式水轮机数值模拟研究[J]. 电网与清洁能源，2016，32(9)：146－150.

Sun Jianbo，Li Ying，Xu Wei，et al. Research on numerical simulation of the Francis turbine based on CFD and FEM[J]. Power System and Clean Energy, 2016, 32(9): 146－150. (in Chinese with English abstract)

[7] 曹鹏彬，肖人彬，库琼. 公理设计过程中耦合设计问题的结构化分析方法[J]. 机械工程学报，2006，42(3)：46－55.

Cao Pengbin, Xiao Renbin, Ku Qiong. Structural analytical approach to coupled design in design with axiomatic design[J]. Chinese Journal of Mechanical Engineering, 2006, 42(3): 46－55. (in Chinese with English abstract)

[8] Yao Tsung Ko. A dynamic planning method for new product development management[J]. Journal of the Chinese Institute of Industrial Engineers, 2010, 27(2): 103－120.

[9] 彭翔，刘振宇，谭建荣，等. 基于多重耦合聚类的复杂产品多变量关联设计模型分解[J]. 机械工程学报，2013，49(3)：111－121.

Peng Xiang, Liu Zhenyu, Tan Jianrong, et al. Multivariable correlative model decomposition for complex product design based on clustering with multiple couplings[J]. Journal of Mechanical Engineering, 2013, 49(3): 111－121. (in Chinese with English abstract)

[10] 陈柏鸿，肖人彬，刘继红，等. 复杂产品协同优化设计中耦合因素的研究[J]. 机械工程学报，2001，37(1)：19－23.

Chen Baihong, Xiao Renbin, Liu Jihong, et al. Research on the coupled factors in MDO for complex products[J]. Chinese Journal of Mechanical Engineering, 2001, 37(1): 19－23. (in Chinese with English abstract)

[11] 袁文强，刘玉生，叶晓平，等. 结合拓扑解耦的多学科优化方法[J]. 计算机辅助设计与图形学学报，2015，27(9)：1795－1804.

Yuan Wenqiang, Liu Yusheng, Ye Xiaoping, et al. A multidisciplinary approach combining with topological decoupling[J]. Journal of Computer-Aided Design & Computer Graphics, 2015, 27(9): 1795－1804. (in Chinese with English abstract)

[12] Sobieszczanski-Sobieski J. A linear decomposition method for optimization problems-blueprint for development[R]. NASA Technical Memorandum 83248, 1982.

[13] 罗兴锜. 水力机械现代设计理论及应用[M]. 西安：西安交通大学出版社，1997.

[14] 高建铭，姚志民. 水轮机的水力计算[M]. 北京：电力工业出版社，1982.

[15] 肖若富，王正伟，罗永要. 基于流固耦合的混流式水轮机转轮静应力特性分析[J]. 水力发电学报，2007，26(3)：120－123.

Xiao Ruofu, Wang Zhengwei, Luo Yongyao. Stress analysis of Francis turbine runners based on FSI[J]. Journal of Hydroelectric Engineering, 2007, 26(3): 120－123. (in Chinese with English abstract)

[16] 阚阚，郑源，赵连辉，等. 基于流固耦合的混流式水轮机转轮强度分析[J]. 水电站机电技术，2015(2)：9－11.

Kan Kan, Zheng Yuan, Zhao Lianhui, et al. Strength analysis of Francis turbine runner based on fluid structure interaction[J]. Mechanical & Electrical Technique of Hydropower Station, 2015(2): 9－11. (in Chinese with English abstract)

[17] 崔军玲，余波，廖翔，等. 基于流固耦合的低水头混流式水轮机转轮叶片静力分析[J]. 水力发电，2017，3(3)：77－80.

Cui Junling, Yu Bo, Liao Xiang, et al. Static analysis of low head Francis turbine runner blades based on fluid-structure interaction[J]. Water Power, 2017, 3(3): 77－80. (in Chinese with English abstract)

[18] 吴广宽，罗兴锜，冯建军，等. 基于瞬态流固耦合的混流式转轮叶片裂纹成因分析[J]. 农业工程学报，2015，31(8)：92－98.

Wu Guangkuan, Luo Xingqi, Feng Jianjun, et al. Cracking reason for Francis turbine blades based on transient fluid structure interaction[J]. Transactions of the Chinese Society of Agricultural Engineering(Transactions of CSAE), 2015, 31(8): 92－98. (in Chinese with English abstract)

[19] Sobol I M. Sensitivity estimates for nonlinear mathematical models[J]. Mathematical Modeling Computational Experiments, 1993, 1 (4): 407－414.

[20] Cukier R I, Fortuin C M, Shuler K E, et al. Study of the sensitivity of coupled reaction systems to uncertainties in rate coefficients: I. Theory[J]. The Journal of Chemical Physics, 1973, 59(3): 3873－3878.

[21] 冯海宽，李振海，金秀良，等. 基于EFAST和PLS的苹果叶片等效水厚度高光谱估算[J]. 农业工程学报，2016，32(12)：165－171.

Feng Haikuan, Li Zhenhai, Jin Xiuliang, et al. Estimating equivalent water thickness of apple leaves using hypersecptral data based on EFAST and PLS[J]. Transactions of the Chinese Society of Agricultural Engineering(Transactions of CSAE), 2016, 32(12): 165－171. (in Chinese with English abstract)

[22] Loubière P, Jourdan A, Siarry P, et al. A sensitivity analysis method for driving the artificial bee colony algorithm’s search process[J]. Applied Soft Computing, 2016, 41: 515－531.

[23] Senthamaraikkannan G, Gates I, Prasad V. Development of a multiscale microbial kinetics coupled gas transport model for the simulation of biogenic coal bed methane production[J]. Fuel, 2016, 167: 188－198.

[24] Jin Ruichen, Chen Wei, Agus Sudjianto. An efficient algorithm for constructing optimal design of computer experiments[J]. Journal of Statistical Planning and Inference, 2005, 134(1): 268－287.

[25] van Griensven A, Meixner T, Grunwald S, et al. A global sensitivity analysis tool for the parameters of multi-variable catchment models[J]. Journal of Hydrology, 2006, 324(1): 10－23.

[26] 朱嘉祺，徐向阳，何爽. 基于 LH-OAT的SWMM 模型参数敏感性分析[J]. 中国农村水利水电，2014(3)：84－87.

Zhu Jiaqi, Xu Xiangyang, He Shuang. An analysis of parameter sensitivity of SWMM model based on LH-OAT method[J]. China Rural Water and Hydropower, 2014(3): 84－87. (in Chinese with English abstract)

[27] 李军，梅琨，张明华. 水质模型的全局参数敏感性分析[J]. 浙江农业学报，2012，24(2)：314－320.

Li Jun, Mei Kun, Zhang Minghua. Global parameter sensitivity analysis on water quality model[J]. Acta Agriculturae Zhejiangensis, 2012, 24(2): 314－320. (in Chinese with English abstract)

[28] Menter F R. Two-equation eddy viscosity turbulence models for engineering applications[J]. AIAA Journal, 1994, 32(8): 1598－1605.

[29] Menter F R, Kuntz M, Langtry R. Ten years of industrial experience with the SST turbulence model[C]// 4th Int. Symp. Turbulence, Heat Mass Transfer, Antalya, Turkey, 2003.

[30] 张丽霞. 混流式水轮机转轮叶片疲劳裂纹控制研究[D]. 北京：清华大学，2010.

Zhang Lixia. Research on Fatigue Crack Control for Francis Turbine Blade[D]. Beijing: Tsinghua University. (in Chinese with English abstract)

[31] Luo Xingqi, Zhu Guojun, Feng Jianjun. Multi-point design optimization of hydrofoil for marine current turbine[J]. Journal of Hydrodynamics, Ser. B, 2014, 26(5): 807－817.

朱国俊，罗兴锜，冯建军，卢金玲，吴广宽.混流式水轮机转轮设计变量耦合强度分析[J]. 农业工程学报，2017，33(22)：36－45. doi：10.11975/j.issn.1002-6819.2017.22.005 http://www.tcsae.org

Zhu Guojun, Luo Xingqi, Feng Jianjun, Lu Jinling, Wu Guangkuan. Variable coupling strength analysis of Francis turbine runner design[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33(22): 36－45. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2017.20.005 http://www.tcsae.org

Variable coupling strength analysis of Francis turbine runner design

Zhu Guojun, Luo Xingqi※, Feng Jianjun, Lu Jinling, Wu Guangkuan

(,,710048,)

Hydropower is one of the most reliable source of green energy and is widely used to meet real-time electricity demand. The ever escalating energy demand and iterative development in hydropower have pushed the generation of hydropower towards a low lost-cost and more flexible state which can work in a wider hydrodynamic region without compromising its performance. So the research on multidisciplinary optimization of hydro turbine needs to be carried out. Francis-type turbine is attractive because the efficiency of the unit at its design point exceeds the other types. As mentioned above, with the needs of robust operation in wide region without compromising its performance, the Francis turbine runner has to be optimized under multidisciplinary constraints. Multidisciplinary optimization technology of Francis runners has always been a key point in the field of turbine research. The coupling strength of each variable is the basis for establishing a concise and efficient multidisciplinary optimization strategy. So in the multidisciplinary optimization of Francis runner, it is necessary to analyze the coupling strength of design variables. In this paper, based on the global relative sensitivity of design variables, a coupling strength analysis method of runner design variables has been presented. First, combing three-dimensional (3D) inverse design theory with curve parametric method, a parametric 3D inverse-design method has been developed to control the Francis runner geometry. According to this parametric 3D inverse-design method, the meridional flow passage and geometry of runner blade can be controlled by a set of discrete parameters. These parameters are treated as runner design variables. The hydraulic efficiency of turbine, the minimal pressure coefficient on runner blade and the maximum static stress of blade are selected as objective functions. Then the global relative sensitivity of each objective function to design variables is calculated by an improved Morris OAT method. Compared with the traditional Morris OAT method, an optimal Latin hypercube design technique is adopted in the improved method. The optimal Latin hypercube design technique has a better space filling property than the traditional one. So the sampling only needs to be done once, which reduces the time of global relative sensitivity analysis without compromising its precision. On the basis of the improved Morris OAT method, the speed of global relative sensitivity calculation is improved obviously. Secondly, the set which contains global relative sensitivity of design variables is treated as universe, and the semi-trapezoidal function in fuzzy mathematics is imported to quantify the membership of each variable to objective functions. After obtaining the membership of each variable, a judgment principle of variable’s coupling strength is presented in this paper. According to this judgment principle, the coupling strength property of each design variable can be defined as strong coupling, middle coupling and weak coupling. Finally, based on the coupling strength of each design variable, the multidisciplinary optimization strategy of Francis runner is established. And then the multidisciplinary optimization of Francis runner can be carried out. In order to validate the coupling strength analysis method, an application case is presented in the paper. In that case, the design variables of a Francis turbine runner with the head of 200 m are chosen as the analysis object. From the analysis result, it can be found that only the coupling strength property of maximum thickness is weak coupling, and the others are middle coupling. According to the result, a multidisciplinary optimization strategy is established and used in the optimization of Francis turbine runner. After optimization, both the hydraulic performance and strength property of the optimized runner are improved, demonstrating the effectiveness of the coupling strength analysis method. In conclusion, the method proposed in this paper can be adopted to analyze the coupling strength of design variables of Francis runner.

optimization; design; computer simulation; Francis runner; global relative sensitivity; coupling strength analyze; improved Morris OAT method

10.11975/j.issn.1002-6819.2017.22.005

TK733+.3

A

1002-6819(2017)-22-0036-10

2017-05-16

2017-08-11

国家自然科学基金项目（51379174、51679195）；国家自然科学基金重点项目（51339005）

朱国俊，博士，讲师，研究方向为流体机械优化设计理论、流动分析等。Email：guojun_zhu1984@126.com

罗兴锜，教授，研究方向为流体机械流动理论及优化设计、流体机械振动与稳定性。Email：luoxq@xaut.edu.cn