模糊层次综合评价法在高科技企业公司治理评价中的应用
沈惠文
(河海大学商学院,南京211100)
模糊层次综合评价法在高科技企业公司治理评价中的应用
沈惠文
(河海大学商学院,南京211100)
将模糊综合评价法运用于高科技企业公司治理评价体系中,构建了层次结构模型,运用层次分析法确定了各指标的权重,并通过专家打分确立模糊评价矩阵,进行多级模糊综合评判。最后得到公司治理评价的综合等级,为公司治理的改善提供参考。
高科技企业;公司治理;模糊综合评价法;层次分析法
引言
近年来,我国高科技产业发展迅猛,成为国民经济新的增长点。高新技术企业是指,在《国家重点支持的高新技术领域》内,持续进行研发和技术成果转化,使企业拥有核心自主知识产权,在此基础上进行经营活动,且在中国境内注册一年以上的居民企业。2013年统计表明,我国高科技企业[1]中,电子和通信设备制造业占比最高,达到47.1%;第二是医药制造业,占27.33%,医疗设备和仪器仪表制造业占18.44%,电子计算机和办公设备制造业占比6%,航空航天制造业占1%。相比传统企业,高科技企业有知识和技术密集,创新性,高增值性及高风险性等特点。在公司治理方面,高科技企业多为人力和非人力资本共同治理;企业的发展较多依赖技术创新。公司治理是公司正确决策和有效管理的基础,对公司治理现状进行合理评价,能够发现问题,促进企业公司治理的完善。本文构建了针对高科技企业的公司治理评价体系,除了公司治理评价的通用指标,特别添加了技术人才激励与约束、技术与创新、风险管理及其下级指标。运用模糊层次综合评价法,即用层次分析法确定各影响因素的权重,用模糊综合评价法确定各方案指标,并根据模糊评价集上的值按最大隶属度原则对对象所属等级进行评定,提高了评价的准确性。
一、高科技企业公司治理评价的步骤
(一)建立因素集X
因素集是指评价指标的集合。由于高科技企业公司治理评价系统具有多层次性,本文将全部指标分为四个层次:第一层是目标层X,即高科技企业公司治理评价水平。第二层是一级指标层Xi,包括公司治理评价的六个方面,即股东、董事会监事会、关键人、信息披露、技术与创新、风险管理。第三层是二级指标层Xij,它们是由六个一级指标分成的12个二级指标。第四层是三级指标层Xijk,它们是由12个二级指标分成的31个具体的评价指标。见表1。
(二)建立评语集Y
评语集用来评价各指标的优劣。四个层次指标的评语集是统一的,本文分为5个等级,即Y=(好,较好,一般,较差,差)=(Y1,Y2,Y3,Y4,Y5),其中,90<Y1≤100,80<Y2≤90,70<Y3≤80,60<Y4≤70,0≤Y5≤60。
(三)建立权重集A
本文采用层次分析法确定权重,衡量了各指标对于评价目标的相对重要程度。各层指标对于上一层的权重的和为1。设A1,A2,…A6是一级指标对目标层的影响权重,则权重集;二级指标对一级指标的权重集三级指标对二级指标的权重集是对应于Aij的三级指标权重。
(四)确立模糊评价矩阵R
(五)进行多级模糊综合评判
由于公司治理评价体系包含多层次指标,最终评价集需要根据多级模糊矩阵运算逐级求出。从最底层的三级指标开始,依专家打分统计得到R,再依公式B=A·R=(b1,b2,…bs),s是评判等级数,,得出二级指标模糊评价矩阵;用同样的算法得出一级指标模糊评价矩阵;同理,根据Y=A·B,最终就得到了总目标的评价集。若最终评价集的,需要归一化, 就可以依最大隶属度原则做出评价结论了。

表1 高科技企业公司治理评价指标体系[2,3]
二、案例——某高科技企业公司治理评价
(一)层次分析法确定权重
专家评估构造判断矩阵,先算出层次单排序。方法是将判断矩阵的每行元素相乘,得到的乘积开n次方,再归一化处理,得到的向量就是单层次权重向量。然后需验证判断矩阵A是否有一致性。由公式AW=λmaxW得出A的最大特征根λmax,然后算出一致性指标 CI和检验系数 CR,CI=(λmax-n)/(n-1),CR=CI/RI,RI代表平均随机一致性指标,见表 2。CR的值越大,说明一致性程度越差。CR<0.1时,说明A通过了一致性检验。当CI=0时,A具有完全一致性。CR≥0.1,需重新建立判断矩阵。
故一级指标对总目标的权重A=(0.258 2,0.129 1,0.25 2,0.074 5,0.159 5,0.120 6)。从排序结果可以看出,在影响高科技企业公司治理评价的一级指标中,股东、关键人的影响均占了25.82%,技术与创新的影响占了15.95%,董事会监事会占12.91%,风险管理占12.06%,信息披露占7.45%。
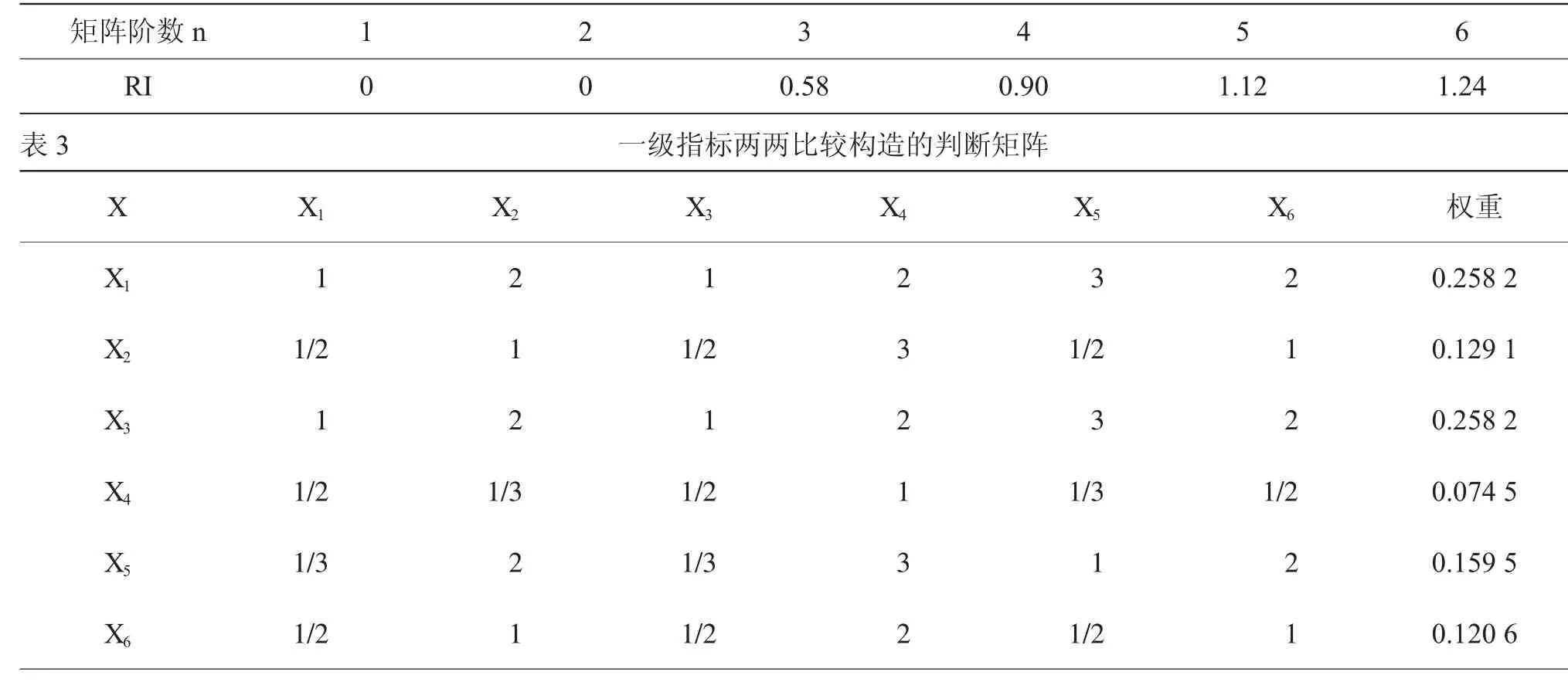
表2 判断矩阵阶数对应的RI的值
同理,求得二级指标对一级指标权重(6个):A1=(0.8,0.2);A2=(0.8333,0.1667);A3=(0.5,0.5);A4=(0.75,0.25);A5=(0.5,0.5);A6=(0.75,0.25),均检验出 CR=0。三级指标对二级指标权重(12 个):A11=(0.75,0.25),CR=0;A12=(0.1429,0.5714,0.2857),CR=0;A21=(0.1449,0.3551,0.3551,0.1449),CR=0.0152<0.1;A22=(0.1005,0.433,0.4665),CR=0.0049<0.1;A31=(0.2,0.6,0.2),CR=0;A32=(0.2599,0.3275,0.4126),CR=0.0462<0.1;A41=(0.75,0.25),CR=0;A42=(0.5,0.5),CR=0;A51=(0.25,0.75),CR=0;A52=(0.5278,0.1396,0.3325),CR=0.0464<0.1;A61=(0.5,0.5),CR=0;A62=(0.25,0.75),CR=0。
(二)专家打分法确立模糊评价矩阵
本文通过专家打分法对每个三级指标依“好,较好,一般,较差,差”进行了等级评定,再算出该指标属于该等级的概率,统计得到12个模糊评价矩阵。

R11表示X111、X112的评价集合,也就是股权构成合理性X111有0.3的概率是等级好,0.5的概率是等级较好,0.2的概率是等级一般;而股权集中度X112有0.2的概率是等级较好,0.1的概率是一般,0.4的概率是较差,0.3的概率是差,评价为差和较差的概率偏高,由此得知该企业的公司治理中的股权集中度有待优化。同理可知,三级指标中的内部人控制、技术人员长期激励薪酬、自行研发专利技术、专利申请数、新产品对营业收入的贡献、信息沟通的有效性等方面需要改善。
(三)多级模糊综合评判的计算
运用公式B=A·R进行第一次模糊矩阵运算。B11=A11·到二级指标的模糊矩阵B1=同理可以得到 B2~B6,


第二次模糊矩阵运算 B1*’=A1·B1,B2*’=A2·B2,B=(B1*,B2*,B3*,B4*,B5*,B6*)T得到一级指标的模糊矩阵B=最后再由Y=A·B进行第三次模糊矩阵运算,就得到综合评价集合 Y=(0.147 8,0.344 6,0.311 8,0.151 1,0.044 7),故而我们可以判断有14.78%的可能性该企业的公司治理水平属于等级“好”,34.46%的概率该企业的公司治理水平属于“较好”,31.18%的把握该企业公司治理水平“一般”,有15.11%的可能性“较差”,也有4.47%的概率其公司治理水平是等级“差”的。由最大隶属度原则,笔者认为,该企业的公司治理水平“较好”[4,5]。如要提高该高科技企业的公司治理评价水平,还需从具体的三级指标进行实际改善。
结语
本文对高科技企业公司治理进行了评价,运用模糊层次综合评价法构建了公司治理评价的层次结构模型,将定性指标予以量化,更为企业提供了公司治理的改善依据。但该模型建立的层次结构模型庞大,计算过程较复杂,专家打分具有主观性,后续还须对模型做进一步改良。需要注意的是,随着企业发展,公司治理的相关利益主体可能进行权力结构配置和调整,公司结构也会常常调整,动态变化,企业的公司治理水平也在相应变化中。
[1]吴晓璐.高科技企业公司治理评价研究[D].合肥:安徽大学,2013:15-53.
[2]李佳.我国高科技企业公司治理对企业投资决策效率的影响研究[D].北京:北京交通大学,2014:8-17.
[3]李梅.我国高科技企业公司治理的分析[J].企业导报,2012,(15):63-64.
[4]谢智学.模糊综合评价在大学生体质健康测试中的应用[J].自动化与仪器仪表,2014,(12):137-139.
[5]夏兴平.基于模糊层次分析法的电信业务网项目后评价研究[J].重庆邮电大学学报:自然科学版,2012,(6):792-797.
F274;F224
A
1673-291X(2017)35-0008-03
2017-05-08
国家社会科学规划基金资助一般项目(15BGL054)
沈惠文(1989-),女,江苏新沂人,硕士研究生,从事财务会计理论与应用研究。
[责任编辑 柯 黎]

