实验室间比对结果的数据处理及测量不确定度评定
张亮亮*
(中航金属材料理化检测科技有限公司,陕西西安,713801)
实验室间比对结果的数据处理及测量不确定度评定
张亮亮*
(中航金属材料理化检测科技有限公司,陕西西安,713801)
某研究总院要求对四组GH4169质控样品中的镍含量进行定值分析,共组织了11家经认证的实验室进行实验室间比对(ILC)。采用了曼德尔 h/k统计分析、科克伦、格拉布斯和狄克逊检验法对数据的一致性和离群值进行了检验。在一致性检验中,对超出临界值hCrit或kCrit数据的取舍情况进行说明,以尽可能地保留超临界数据,使统计结果更为真实、可靠。再利用赋值合理的3个水平的实验数据和期间精密度条件下的质控数据,分别计算偏倚ub和不精密度uR’两者带来的累积效应,以作为不确定度的估计量进行评定。
实验室间比对(ILC);一致性检验;离群值检验;测量不确定度评定
引言
高温合金GH4169(INCONEL 718)是以体心四方的γ''相和面心立方的 γ'相沉淀强化的镍-铬-铁基高温合金,由于该合金具有较高的强度、良好的抗蠕变和抗疲劳性能,以及优越的综合力学性能,因而在航空上主要用于发动机部件,如涡轮盘、叶片、机匣、轴、定子、封严、支撑件、管路、紧固件等。要准确测定GH4169合金中化学成分是判定材料是否合格的重要环节。某研究总院在召开关于GH4169材料化学成分分析报告中指出,各检测机构给出镍的测定结果相差较大,而镍作为主要基体成分对材料的性能有着极为重要的影响。为分析原因,将四组GH4169质控样品分发给11家有资质的实验室,要求各实验室按标准进行检测。
一些研究表明[1-4],采用曼德尔h/k一致性统计分析检查ILC数据的可靠程度,相比其它统计方法[5-9],h/k检验方案更显得简捷直观。本文对各实验室的ILC数据也采用h/k一致性统计分析。并采用 top-down技术[10-12]评定丁二酮肟-EDTA容量法测定GH4169标样中镍含量的不确定度,top-down技术是在期间精密度测量条件下,利用质控和方法确认数据,分别将偏倚 ub和不精密度 uR’两者带来的累积效应,作为不确定度的估计量进行评定。该评定方法操纵性强、易于推广。
1 实验部分
文中数据摘自某研究总院组织 ILC实验结果,组织分发给11家检测机构各四组GH4169质控样品。对于标准分析方法的选用,有2家实验室(1#和2#)选用丁二酮肟重量法[13],其余9家实验室选用丁二酮肟沉淀-EDTA容量法[14]。
评定uR’的数据源自本实验室期间精密度条件下,GH4169质控样品(52.27%±0.07%,编号:YSBC 41503-2012,研制单位:上海材料研究所)两个月的累积数据,分析方法为丁二酮肟沉淀-EDTA容量法[14]。
2 结果与讨论
2.1 一致性检验
2.1.1 k统计量检验
k是实验室内数据一致性的统计量,对各试验结果进行离散型统计分析,即单个实验室内各试验结果与试验结果均值在相比其它实验室下的偏差。设有p家实验室(j)参加比对,n是单个实验室内试验结果数量(x1,j,x2,j,…xi,j…xn-1,j,xn,j),试验室(j)的k统计量见公式(1-4)。
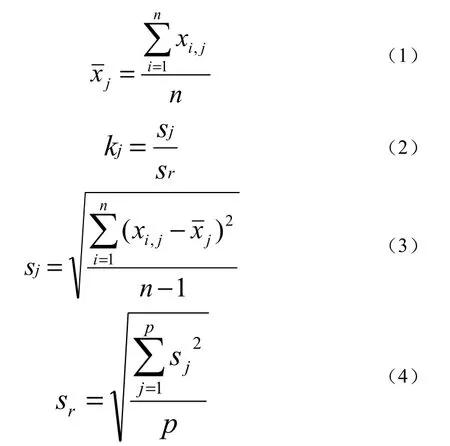
kcrit是衡量测定结果离散程度的检验临界值,见公式(5),当k值超过临界值kcrit,表明试验结果离散程度非常严重,精密度很差,试验结果难予接受。

F(ν1,ν2)为 F-F 分布,自由度 ν1=n-1,ν2=(p-1)(n-1),该值即可通过F分布表获得,也可由Excel函数“=FINV(0.05,ν1,ν2)”获得。
2.1.2 h统计量检验
h是实验室间数据一致性的统计量,确定是否有实验室的数据是离群的,即单个实验室结果均值与所有实验室结果均值的偏差。h值越大,说明试验结果偏差越大,结果准确度越低。设有p家实验室(j)参加比对,各实验室内试验结果数量(),试验室(j)的h统计量见公式(6-9)。


hcrit是衡量单个实验室测定结果准确度的检验临界值,见公式(10),当h值超出临界值hcrit,表明试验结果准确度很差,试验结果不予接受。

t为学生氏概率分布值,其自由度ν=p-2,该值即可通过t分布表获得,也可由Excel函数“=TINV(0.05,ν)”获得。
表1给出了检出水平α=0.05时,Mandel’s h/k统计量临界值。
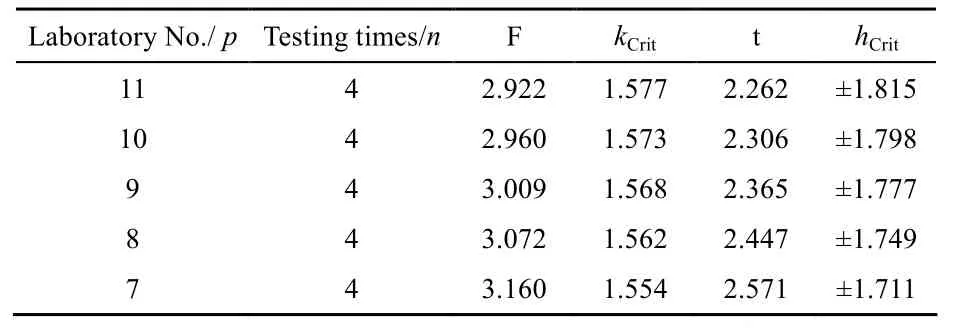
表1 曼德尔h/k统计量临界值(α=0.05)Table 1 The critical value of Mandel’s h/k statistic (α=0.05)
为了尽可能合理的保留各实验室上报的ILC试验数据,首先通过h/k统计公式计算出各实验室的h(j)值和k(j)值,先判定h(j)值是否超出临界值hCrit,若超出hCrit,则应先剔除该组实验室数据,重新计算新一轮的h(j)值和k(j)值,直至h(j)值是在hCrit之内。然而,在运算时存在不断会有新一轮的h(j)值超出 hCrit,但对于略高于hCrit的h(j)应予以保留,否则,若ILC数据牺牲太大,统计结果不能客观反映各实验室间的检测情况。当h(j)判定完成后,再判定预留数据 k(j)值,允许稍高于临界值的 k(j)值,但若 k(j)高出kCrit太多,就应考虑舍去。
表2为各实验室上报的GH4169质控样品中镍含量的统计结果。表中再现性精密度标准差 sR和偏倚 bi的计算见公式(11)和(12),式中,ARV为样品接受参考值或标准认可值。


表2 GH4169货控样品中镍含量的ILC研究(%)Table 2 ILC study of nickel content in GH4169 quality control sample (%)
备注:表中的灰色背景表示该h值或k值统计量超出其临界值,继而在下一次统计运算时将该实验室的试验结果予以剔除;被标上标的数据为按执行h/k统计检验次序得出的h值或k值,若未标记,即为最后一次统计检验结果。如标记为ⅰ时,即第一次对所有实验室的数据值进行统计运算;标记为ⅱ时,即第二次对剩余实验室的数据值进行统计运算,依次类推。
为了便于分析统计情况,通常采用直方图对统计结果进行表述,如图1所示,为①号样品中镍含量的h/k统计分布直方图。

图1 试验结果的h值和k值统计量分布直方图Fig.1 Statistic distribution histogram of h value and k value for test results
表3至表5是各实验室给出的②~④号GH4169质控样品中镍含量统计结果。

表3 GH4169货控样品中镍含量的ILC研究(%)Table 3 ILC study of nickel content in GH4169 quality control sample (%)

表4 GH4169货控样品中镍含量的ILC研究(%)Table 4 ILC study of nickel content in GH4169 quality control sample (%)

表5 GH4169货控样品中镍含量的ILC研究(%)Table 5 ILC study of nickel content in GH4169 quality control sample (%)
由表2~表5的统计结果可以看出,在最后保留的数据中,虽有个别实验室的 h值或 k值超出其临界值,如表3中h(j=3)=1.81>+1.798,k(j=10)=1.73>1.573,但 h(j)值与临界值极为接近,k(j)只是略高于其临界值,分析认为是随机误差所致,在统计时应予以保留。
另外,通过以上分析可以看出:1)与其它实验室相比,4#实验室的准确度和精密度均较差;2)1#实验室的准确度稍差;3)7#实验室和 10#实验室的精密度稍差。这就要求相关实验室需对其实验过程进行质量自查和原因分析,在确保检测数据真实和可靠的同时,进一步提高实验室检测水准。
总得来说,由该研究总院组织的ILC研究基本成功,除了②号样品赋值与各实验室的平均值差异较大外,其它3组的赋值都比较合理。
2.2 离群值检验
2.2.1 科克伦检验[15]
该统计方法是对标准差的最大值进行评定,属于单侧检验。统计过程是先将实验室结果标准差由小到大排列,然后根据标准差的最大值计算科克伦检验的统计量,见公式(13)。查阅Cochran临界值表,通过与同一显著水平下的临界值进行比较,判定最大标准差是否为离群值。如果标准差的最大值是离群值,则将该值舍去后对剩余的标准差重新计算科克伦检验的统计量。

式中,Ci是i水平下科克伦检验的统计量值,sj是实验室内标准偏差,sjmax是sj中最大值。
离群值的判定:
a)当统计量小于等于5%的临界值时,认为该值是正常值;
b)当统计量大于5%的临界值且小于等于1%的临界值时,该值为可疑值;
c)当统计量大于1%的临界值时,认为该值是离群值。
应用科克伦检验,对4个水平保留实验室的方差进行统计运算,统计量C值见表6。

表6 各水平方差的科克伦检验Table 6 Cochran test of variance with different levels
检验结果表明,各水平的实验数据无离群值和可疑值。
2.2.2 格拉布斯检验[15]
格拉布斯检验法是用于判定一组数据中最大值或最小值是否为离群值,属于双侧检验。统计过程是先将实验室结果由小到大排列,并得出该组数据的平均值和标准偏差然后再计算统计量G,见公式(14-16)。查阅Grubbs检验临界表,通过与同一显著水平下的临界值进行比较,判定该试验值是否离群。若数据为离群值,再对剩余数据继续检验,直至数据中无离群值为止。

其中,xp是数据xi(i=1,2,…p)中的最大值,是i水平下数据平均值的标准偏差。

式中,x1为数据xi(i=1,2,…p)中的最小值,是i水平下数据平均值的标准偏差。

离群值的判定:
a)当统计量小于等于5%的临界值时,认为该值是正常值;
b)当统计量大于5%的临界值且小于等于1%的临界值时,该值为可疑值;
c)当统计量大于1%的临界值时,认为该值是离群值。
应用格拉布斯检验,对4个水平保留实验室的x进行统计运算,统计量G值见表7。

表7 各水平平均值的格拉布斯检验Table 7 Grubbs test of mean with different levels
检验结果表明,各水平的实验数据无离群值和可疑值。
2.2.3 狄克逊检验[15]
在异常值检验过程中,重复使用狄克逊检验法的效果比格拉布斯检验法要优越得多,方法有单侧检验和双测检验。本文采用双侧检验法,统计过程是先将实验室结果由小到大排列,即x1≤x2≤...≤xmax-1≤xmax,然后再计算统计量 D,见公式(17-19)。查阅Dixon检验临界表,通过与同一显著水平下的临界值进行比较,判定该试验值是否离群。若数据为离群值,再对剩余数据继续检验,直至数据中无离群值为止。

离群值的判定:
a)当统计量小于等于5%的临界值时,认为该值是正常值;
b)当统计量大于5%的临界值且小于等于1%的临界值时,该值为可疑值;
c)当统计量大于1%的临界值时,认为该值是离群值。

表8 各水平平均值的狄克逊检验Table 8 Dixon test of mean with different levels
检验结果表明,各水平的实验数据无离群值和可疑值。
由此可以看出,通过以上三种离群值检验法,4个水平的实验数据均无离群值和可疑值。这也说明经h/k一致性检验保留的实验数据更为合理,统计结果可靠。
2.3 不确定度评定
2.3.1 ub的评定
依据之前的统计结果,选用其中3组赋值合理的质控样品进行偏倚不确定度评定,ub的统计量参见公式(20)。

其中,ub是偏倚的不确定度分量;n是样品数;是uCref的平均值,当 ARV用中位值或稳健平均值表示时,有用表示时,有L为参加实验室数。通过赋值计算,得出ub=0.202%。
2.3.2 uR’的评定
本实验室选用在期间精密度条件下,GH4169质控样品(52.27%±0.07%)在两个月内的累积数据,按时间顺序记录,结果见表9。通过 Anderson Darling(AD)统计量检验表明(A2(s)=0.204,A2*(s)=0.211,A2(MR)=0.424,A2*(MR)=0.438),实验室数据处于统计受控状态,即有uR’=sR’=0.059%。

表9 货控样品中镍含量测定结果(%)Table 9 Determination results of nickel content in quality control sample (%)
2.3.3 合成不确定度
已知 ub=0.202%,uR’=0.059%,进而采用公式(21)计算合成不确定度uc=0.21%。

因此在 95%概率下,GH4169质控样品的测定结果为52.27%±0.42%,k=2。
3 结束语
本文首先采用曼德尔h/k统计分析对参与ILC的11家实验室试验数据的一致性进行了检验,对超出临界值hCrit或kCrit的实验数据判定其取舍。然后采用科克伦、格拉布斯和狄克逊检验法对各水平保留的实验数据进行了离群值检验,检验结果表明经h/k一致性检验所保留的实验数据更为合理,统计结果可靠。最后利用赋值合理的 3个水平的实验数据和本实验室期间精密度条件下的质控数据,分别计算偏倚ub和不精密度uR’两者带来的累积效应,以作为不确定度的估计量进行评定。此外,为了使ub的评定结果更加准确,在以后的分析中应尽可能加大各水平间的梯度值,且在兼顾风险和成本的前提下,应尽可能增大样本容量,以给出更为合理的不确定度估计量。
[1]徐本平.精密度试验中的数据处理[J].冶金分析,2013,33(11): 74-80.
[2]裴文,田洪祥,刘瑜,等.发射光谱仪检测油料的精密度[J].光谱实验室,2011,28(4): 597-1602.
[3]黄文通,吴卓成.沥青混合料比对实验一致性分析[J].石油沥青,2008,22(5): 56-58.
[4]冯俊杰,齐小勇.车载式路面激光平整度仪实验室间比对结果分析[J].公路交通科技:应用技术版,2013,07: 20-23.
[5]符颖操,罗茜.实验室间比对结果分析统计方法的探讨[J].理化检验:物理分册,2006,42(6): 295-299.
[6]陆娟.一次实验室间比对试验结果分析[J].现代预防医学,2013,40(14): 2700-2702.
[7]陈东,蔡健.海洋环境监测实验室间比对试验结果分析评价[J].化学分析计量,2012,21(5): 79-81.
[8]王承忠.实验室间比对的能力验证及应用实例[J].理化检验:物理分册,2009,45(7): 423-430.
[9]Hayes K,Kinsella A,Coffey N. A note on the use of outlier criteria in Ontario laboratory quality control schemes [J]. Clinical Biochemistry,2007,40(3-4): 147-152.
[10]International organization for standardization. ISO 11352: 2012(E)Water quality-Estimation of measurement uncertainty based on validation and quality control data [S]. Published in Switzerland,2012.
[11]中国合格评定国家认可委员会.CNAS-GL34: 2013基于质控数据环境检测测量不确定度评定指南[S].北京:国家认证认可监督管理委员会,2013.
[12]Magnusson B,Naykki T,Hovind H,et al. Handbook for calculation of measurement uncertainty in environmental laboratories [S]. Nordtest,NT Technical Report 537,NT Progect No. 1589-02,Espoo,Edition2,2004-02.
[13]冶金工业部钢铁研究总院,上海钢铁研究所. GB/T 223.25-1994 钢铁及合金化学分析方法 丁二酮肟重量法测定镍量[S].北京:中国标准出版社,1994.
[14]中国航空工业第一集团公司北京航空材料研究院,哈尔滨东安发动机(集团)有限公司,西安航空发动机公司,沈阳黎明发动机制造公司. HB 5220.23-2008 高温合金化学分析方法 第 23部分: 丁二酮肟沉淀-EDTA容量法测定镍含量[S].北京:中国航空综合技术研究所,2008.
[15]邓勃.分析测试数据的统计处理方法[M].北京:清华大学出版社,1995.
Data Processing of Inter-laboratory Comparison Results and Evaluation of Measurement Uncertainty
ZHANG Liangliang*
(AVIC Metal Test Technology Company Limited,Shanxi Xi'an,713801,China)
A study was conducted to determine the nickel content in four groups GH4169 quality control samples,and eleven accredited laboratories were organized to conduct inter-laboratory comparison (ILC) study. The data consistency and outliers were investigated with Mandel’s h/k statistic analysis,Cochran,Grubbs and Dixon test methods. In order to make the statistical results more realistic and reliable,the supercritical data that is beyond the critical value hCritor kCritshould be retained as soon as possible in the consistency test. Reservation or deletion of the supercritical data was explained. Using three levels of reasonable experimental data and quality control data under the condition of period precision calculated respectively bias uband imprecision uR’,the cumulative effect of the both was evaluated as measurement uncertainty.
Inter-laboratory comparison study (ILC); consistency test; outliers test; measurement uncertainty evaluation
O212.1
A
1672-9129(2017)06-0094-05
10.19551/j.cnki.issn1672-9129.2017.06.033
张亮亮. 实验室间比对结果的数据处理及测量不确定度评定[J]. 数码设计,2017,6(6): 94-98.
Cite:ZHANG Liangliang. Data Processing of Inter-laboratory Comparison Results and Evaluation of Measurement Uncertainty[J]. Peak Data Science,2017,6(6): 94-98.
2017-01-23;
2017-02-26。
张亮亮(1986-),男,陕西西安,助理工程师,硕士研究生,研究方向:化学分析。
E-mail:aconsery@sina.com

