降雨三步抗差修正效果的研究

王玉丽 包为民

(河海大学 水文水资源学院， 南京 210098)

降雨三步抗差修正效果的研究

王玉丽 包为民

(河海大学 水文水资源学院， 南京 210098)

在分析流域降雨分布规律的基础上，利用三步抗差方法修正遥测降雨观测资料中的异常误差．采用陆水流域的11场洪水降雨资料，加上人工生成的不同量级的误差系列，计算比较各步抗差修正的有效性．计算结果表明：在不同量级的异常误差下抗差修正方法是有效的，第一、二、三步相结合的效果最好，一二步结合的效果次之，且随着误差量级的增大抗差有效性增强．

三步抗差； 遥测降雨； 陆水流域； 效果

降雨作为洪水预报系统的重要输入项，其精度直接影响洪水预报的精度，雨量资料的误差是洪水预报模型误差的重要来源[1]．遥测系统能够实时准确快速地将降雨量存入数据库，一定程度上提高了降雨资料的时效性，但也存在着误差．水文遥测系统的误差有两类，一是随机观测误差，二是有偏误差，把含有偏观测误差的降雨观测值视为异常值[2]．将抗差估计方法引入到遥测降雨观测中，利用抗差抵御异常值污染的特性对降雨资料进行修正，确保降雨资料在进入洪水预报系统之前正确无误．

1 方法介绍

具体函数形式为：

每个时段都建立式(2)的降雨函数，其中Ji、Wi表示第n站对应的经纬度，Ri表示该时段的第i站降雨量．因此上式中的7个参数是时变的，即每个时段都会率定出一组参数．

式(2)表示成矩阵形式：

其中

其中n为雨量站的个数．

采用最小二乘法求得的参数X可表示为：

若降雨观测资料中含有异常值，会导致率定出的参数是不精确的，因此引入抗差估计方法与最小二乘法相结合，即抗差最小二乘法求得的参数估值为[6-9]：

式中，P为权阵，其初始值为单位阵I．

式中，σ为加权残差均方差；ε为残差；k1、k2为常数，由未加入异常误差情况下的理想模型试算后取k1=2.7，k2=3.5．

三步抗差修正的第一步是针对时段降雨量，第二步对时段降雨量绝对离差，第三步是对时段降雨量的模拟绝对误差．一个流域的时段降雨量、时段降雨量绝对离差和时段降雨量模拟绝对误差都分布在一定范围内并且有一定的分布特征．根据这些分布特征可以提出以下特征函数[10-14]：

其中的Xi在第1步、第2步和第3步中分别代表时段降雨量、时段降雨量绝对离差和时段降雨量模拟误差．k1、k2是常数，决定着正常区、降权区和淘汰区的大小．

计算步骤：1)分析所有雨量站降雨资料的统计特征，进行排频确定各步的k1、k2值；2)对所有时段降雨量资料，采用相应的抗差特征函数进行误差修正；3)对步骤2)修正后的降雨资料计算时段降雨量绝对离差，利用相应的抗差特征函数进行修正；4)对步骤3)修正后的降雨资料通过式(1)计算时段降雨模拟绝对误差，再利用相应的抗差特征函数修正.

式中，μi为不服从正态分布的低频率误差；R为随机数；emax为影响生成误差大小的常数；T为异常值产生的间隔，控制异常误差产生的间隔频率．

2 应用检验

陆水流域位于湖北省东南部，是长江中游南岸的一级支流，发源于湘鄂赣3省交界的幕阜山北麓通城县境内的黄龙山，流经通城、崇阳、赤壁、嘉鱼4县(市)．整个流域位于北纬29°05′～29°50′，东经113°40′～114°10′．流域面积3 950 km2．干流全长183 km[15]．采用陆水水库11场洪水降雨资料加上式(8)生成不同量级的人工误差，所构成的一系列具有异常误差的降雨观测资料来进行抗差效果的研究，考虑了当1个站、2个站和4个站有异常值情况下的各步修正效果，其中误差添加的雨量站和时段都是随机的．

先对所有雨量站的降雨资料进行排频计算，其分布如图1所示．可以看出陆水流域的时段降雨量主要分布在[0，30]mm区间上，其中[0，10]mm为高频区，频率为98.16%，[10.1，30]mm发生频率为1.84%．时段降雨量绝对离差和时段降雨量模拟绝对误差的排频与降雨量的相似．确定各步的临界值k1和k2值见表1．

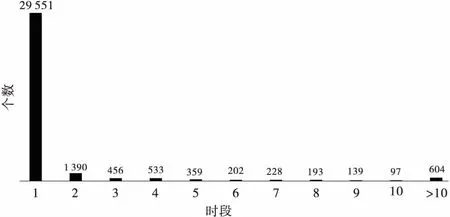
图1 陆水水库降雨频率分布

临界值时段降雨量/mm时段降雨量绝对离差/mm时段降雨量绝对模拟误差/mmk11187k2292012

3 结果与分析

因为三步抗差修正在一个站、两个站和四个站发生异常误差情况的变化规律相似，现以一个站出现异常情况为例进行说明．

不同量级异常误差情况下的三步抗差效果见表2，三步抗差的修正效果(以一个站有异常误差为例)如图2所示．由表2可以看出在不同量级的误差情况下，三步抗差的效果不同．结合表2和图3，可以发现对于小误差，第二步的效果比第一、三步的效果好，第三步的效果也比大误差时好．对于大误差，第一步的效果较好，第二、三步的修正效果则变弱．这是因为异常误差越大，异常值就会越容易被识别出来并得到修正，当第一步抗差效果很好时，余留给第二、三步的误差则会变小，就会放大修正效果，导致后两步有效系数很小．反之，当第一步的修正效果不好时，余留和后两步的误差变大，相应的修正效果也会越明显．可以看出三步在修正过程中相互弥补．随着误差量级的增大，总的修正效果越好．结果中出现负值可能是抗差过度所引起的．

图2 三步抗差的修正效果(以一个站有异常误差为例)

emaxr11r12r13r1tr21r22r23r2tr41r42r43r4t100．3180．4750．0860．3550．1800．0500．0670．0670．1050．052-0．0010．151200．4060．4100．0300．6600．3120．412-．0970．5560．1700．3750．0110．487300．4530．1970．0620．5880．4480．2580．1100．6360．4160．367-0．0530．610400．6310．151-0．0620．6680．6230．2120．1070．7350．5480．3410．0550．718500．7360．119-0．2920．6990．7000．586-．2100．8500．6170．398-0．0620．755600．7750．109-0．0890．7810．7480．131-．1250．7540．6570．459-0．1170．792700．8160．080-0．0970．8150．7770．1390．1520．8370．6720．5110．0010．840800．8420．0450．0330．8540．7950．2060．0200．8400．6880．548-0．0540．851900．8580．0320．0490．8690．8040．2870．0100．8620．6940．577-0．4210．8161000．8700．018-0．1260．8560．8190．3420．0290．8840．7070．602-0．1270．8692000．9100．308-0．0120．9370．8460．649-．0290．9440．7260．683-0．0330．910均值0．6920．177-0．0380．7350．6410．2970．0030．7240．5450．447-0．0730．709

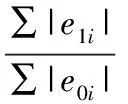
当一个站发生异常误差时第一、二、三步以及总的修正平均效果为0.692、0.177、-0.038、0.736；当两个站发生异常误差时则为0.641、0.297、0.003、0.724；当四个站有异常误差时的效果分别为0.545、0.447、-0.073、0.709．可看出随着发生异常值站数的增多，第一步抗差效果会稍变差，第二修正效果越好，第三步的修正效果不稳定，这是因为随着发生异常值站数的增多，抗差探测异常值的效率降低，进而导致修正有效性略低．

各步抗差修正效果见表3．计算三步抗差中各步的抗差效果，结合表2、3可以看出，当一个、两个、四个站有异常值时，第一步修正效果为0.692，0.641，0.545，第二步修正效果为0.673，0.656，0.578，第三步的效果为0.177，0.178，-0.025，一二步结合的效果为0.729，0.715，0.692，一三步结合的效果为0.575，0.611，0.512，一二三步的效果为0.735，0.724，0.709．第一步的修正效果明显比第二、三步好，而第二步的效果又比第三步的好．单独的第二、三步和一、三步结合在小误差情况下修正效果很差，甚至出现负值．而一、二步结合修正时在小误差情况下效果好．一、二、三步结合的效果比一、二步结合和一、三步结合的效果好，其中一二步结合比一三步结合的效果好．

表3 各步抗差修正效果

4 结 论

1)不同量级的异常误差情况下，遥测降雨的三步抗差效果不同．误差量级越大，抗差效果越好．

2)随着发生异常误差站数的增加，由于异常值被探测效率的降低，导致修正效果降低．

3)第一、二、三步结合的抗差效果比第一步和一二步结合的修正效果好，其中一、二步结合的效果比第一步的好．在三步抗差的过程过各步相互弥补，得到较高的修正有效性．

4)临界值k1、k2是通过试算的方法确定的，具有一定的主观性．因此对于确定k1、k2值得方法有待进一步的研究．

[1] 包为民，瞿思敏，等．遥测系统降雨观测误差估计方法研究[J]．水利学报，2003，34(4)：30-34．

[2] 赵 超．流域实时洪水抗差预报系统研究[D]．南京:河海大学，2006．

[3] 瞿思敏．抗差理论在洪水预报中的应用研究[D]．南京:河海大学，2004．

[4] 瞿思敏，包为民，石 朋，等．降雨观测粗差修正方法研究[J]．武汉大学学报，2005，38(6):32-34．

[5] 周江文，黄幼才，杨元喜，等．抗差最小二乘法[J]．武汉:华中理工大学出版社，1997．

[6] 包为民，嵇海祥，等．抗差理论及在水文学中的应用[J]．水科学进展，2003(4)．

[7] A.Bárdossy， Singh S K． Robust Estimation of Hydrological Model Parameters[J]． Hydrology and Earth System Sciences，2008(12): 1273-1283．

[8] 包为民，林 跃，黄贤庆，等．水库入库河段洪水汇流参数抗差估计研究[J]．武汉大学学报：工学报，2004，37(6):1127-1129．

[9] 包为民，瞿思敏，等．水文系统抗差权函数分析与检验[J]．清华大学学报:自然科学版，2003(8):1127-1129．

[10] Zhao C，Hong H S，Zhu M L． A Three-stepwise Robust Statistical Method for Outlying Rainfall Observation[J]．Journal of the Graduate School of the Chinese Academy of Sciences，2010，27(1):17-26．

[11] 欧吉坤．一种三步抗差方案的设计[J]．测绘学报，1996，25(3):173-179．

[12] Li Qian，Bao Weimin，Qian jinglin． An Error Updating System for Real-time Flood Forecasting based on Robust Procedure[J]．KSCE Journal of Civil Engineering， 2015，19(3):796-803．

[13] Rousseeuw P J，Leroy A M． Robust Regression and Outlier Detection[M]． John Wiley&Sons，NewYork，1987．

[14] Tsuyoshi Hashimoto，Daniel P Loucks，Jery R.Stedinger，Robustness of Water Resources Systems，Water Resources Res，2003，18(1):21-26．

[15] 程孟孟，杜成寿，郑桂平．陆水流域水文特性分析[J]．人民长江，2013，44(18)：56-58．

StudyofThree-stepwiseRobustCorrectEffectofRainfall

Wang Yuli Bao Weiming

(College of Hydrology & Water Resources, Hohai Univ., Nanjing 210098, China)

Based on the analysis of rainfall distribution in the basin,the three-stepwise robust method is used to correct the outliers in the telemetric rainfall observation data. Eleven floods rainfall data of Lushui basin are used; and the error series of different magnitudes are calculated and compared. The results show that: the robust correction method is effective; the combination of the first, second and third steps has the best effect; the combination of first and second steps followed. Furthermore, the effect is better with the increase of the error magnitude.

three stepwise robust； telemetry rainfall； Lushui basin； effect

10.13393/j.cnki.issn.1672-948X.2017.05.007

2016-11-30

国家自然科学基金面上基金(51279057/51479062)；水利部公益性行业科研专项项目(201501059)．

王玉丽(1992-)，女，硕士生，主要从事水文水资源和水文预报方面的研究．E-mail：yuliwang8943@163.com

P332

A

1672-948X(2017)05-0034-04

[责任编辑王迎春]