边坡稳定分析中圆弧与折线滑动面对比分析研究

李建举 李玉莹

(1.中国航空港建设第九工程总队，成都 611430； 2. 长安大学 公路学院，西安 710064)

边坡稳定分析中圆弧与折线滑动面对比分析研究

李建举1李玉莹2

(1.中国航空港建设第九工程总队，成都 611430； 2. 长安大学 公路学院，西安 710064)

以分析圆弧和折线两种滑动面以及简化Bishop法和通用条分法两种方法对边坡稳定分析结果的影响为目标，基于极限平衡理论，采用边坡稳定分析软件Zslope，以均质边坡、加筋边坡以及成层土非均质边坡为例，计算中采用圆弧和折线两种滑动面，以及简化Bishop法和通用条分法两种极限平衡方法，分析比较其安全系数和临界滑动面的差异．研究结果表明，当滑动面为圆弧滑动面时，简化Bishop法与通用条分法计算得到的安全系数和临界滑动面位置基本相同；与圆弧滑动面相比，折线滑动面得到的安全系数偏小，对于加筋边坡以及非均质边坡，折线与圆弧滑动面搜索到的安全系数差别可能会较大，圆弧滑动面容易陷入局部极值，而折线滑动面则更有利于搜索到全局极值．研究成果对于边坡工程设计具有一定的参考价值．

边坡稳定； 圆弧滑动面； 折线滑动面； 安全系数； 通用条分法

边坡稳定分析是岩土工程领域研究的热点问题，其分析方法也一直是学者们研究的重点之一．自从瑞典人彼德森最早提出极限平衡条分法的概念之后[1]，许多学者对于极限平衡理论及其在边坡稳定分析中的应用展开研究，丰富了这一领域的研究成果．基于极限平衡理论的条分法仍然是目前为止工程中常用的边坡稳定分析方法，为广大工程师所熟悉．

在瑞典条分法之后的研究过程中出现了一系列数值分析算法，主要包括适用于非圆弧滑动面的通用条分法、更适用于实际工程的倾斜条分法、能够准确进行理论计算的三维极限平衡法等[2]．卢坤林等[3]将空间内土条划分后条柱间的作用力看作滑动面上的正应力，根据整个滑动土体的静力平衡条件建立方程，提出了一种适用于一般三维滑动面形式的极限平衡法；白桃等[4]为了考察空间内土体参数变异时极限平衡法的适应性，对极限平衡法4种不同算法下得到的安全系数进行了比较，并提出采用安全系数和破坏概率2个指标能够定量化地表述边坡稳定性．王旭等[5]考虑到土体参数变异性和随机性对边坡稳定性的影响，提出将可靠度方法得到的可靠度和破坏概率等指标与确定性方法相结合，可以更好地评价边坡的稳定性；邓东平等[6]基于摩尔-库伦强度理论和滑动面法向力的计算，根据空间内土体的静力平衡条件，提出对于三维滑动土体可以采用不完全满足所有平衡条件的准严格法求解安全系数．代凌辉等[7]采用有限元软件计算分析了抗滑桩的桩长和桩径等参数对于抗滑桩加固后的边坡的安全系数和临界滑动面的影响．但是以往的研究主要集中在极限平衡分析方法对于计算结果的影响上，滑动面的形状对于边坡安全系数以及临界滑动面的影响仍无系统研究，对于均质土坡研究较多，对于加筋边坡以及非均质边坡的研究较少，本文基于边坡稳定分析软件ZSlope，分别设置圆弧滑动面和折线滑动面为初始滑动面，采用极限平衡法中的简化Bishop法和通用条分法两种算法计算，通过均质土边坡、加筋边坡和非均质土边坡算例的计算，比较不同算法得到的安全系数和临界滑动面，归纳总结相应规律，为边坡稳定分析方法的选取提供参考．

1 基本理论

极限平衡法是将滑动土体划分为若干个垂直土条后，分析所划分土条的力和力矩平衡条件，根据静力平衡方程进行分析和计算．该方法假设滑动面发生滑动造成土体破坏，滑动土体服从破坏条件，且土体内滑动面已知[8]．不同的算法采用不同的土条间相互作用关系，也适用于不同的滑动面形状．根据条间力假定的不同，极限平衡法可分为两大类：一类是只满足力与力矩平衡的部分静力平衡条件的方法，例如瑞典条分法、简化Bishop法、简化Janbu法，另一类是严格满足力与力矩平衡的所有静力平衡条件的方法，如Spencer法、Morgenstern-Price法、通用条分法等．

1.1 简化Bishop法

最初毕肖普提出将土体的抗剪强度指标，即粘聚力c和内摩擦角φ的正切值tanφ分别降低为c/F和tanc/F，然后根据静力平衡条件建立方程，其中F即为稳定安全系数；简化Bishop法则是以圆弧滑动面为基础，假设只考虑土条间的水平作用力，忽略切向剪应力的影响，根据滑动面的静力平衡条件求解安全系数[9]．

1.2 通用条分法

通用条分法满足条间力、力与力矩平衡的所有静力平衡条件，并将其合力的大小和方向作为未知数，通过多次定义条间力的倾角函数，经数值迭代求解后，判断是否满足静力平衡条件进而判定其安全系数，该方法既适用于圆弧滑动面，也适用于折线滑动面[9-11]．

1.3 ZSlope软件简介

ZSlope是一款基于极限平衡理论的边坡稳定分析软件[12]．该软件系统不仅提供了规范中所有安全系数求解算法，如瑞典法、简化Bishop法、简化Janbu法、不平衡推力法、通用条分法GLE、Morgenstern-Price法、Spencer法等．软件提供了5种临界滑面搜索算法，其中，圆弧滑动面搜索方法为穷举法[12]，折线形滑动面搜索方法采用常值转角法、随机转角法、节点移动法和变常值转角法[13-15]．本文对于折线滑动面的搜索方法是改进的Monte-Carlo搜索算法，即常值转角法，该方法把随机转角变为了具有更大的搜索范围和更高稳定性的常值转角，使之受初始滑面的影响更小，因此具有更强的适应性[15]．

2 算例分析

本文以均质边坡、加筋边坡以及成层土非均质边坡为例，对比分析不同形状的初始滑动面和不同的算法对安全系数及临界滑动面的影响．

2.1 均质边坡

2.1.1 基本计算模型及参数

首先分析一均质边坡，坡比为1∶0.25，边坡高度12 m，地基厚度6 m，其基本计算模型尺寸如图1所示，土体参数见表1．

图1 算例1计算模型(单位：m)

算例容重γ/kN·m-3饱和容重γsat/(kN·m-3)内摩擦角φ/°粘聚力c/kPa1、218．020．020．035．0

以均质边坡为例的条分法划分如图2～3所示，土条划分数n为25条．

图2 圆弧滑动面条分法划分简图(单位：m)

图3 折线滑动面条分法划分简图(单位：m)

2.1.2 结果分析

经分析计算后，得到的安全系数及其相应临界滑动面(见表2和图4)．

表2 算例1安全系数计算结果

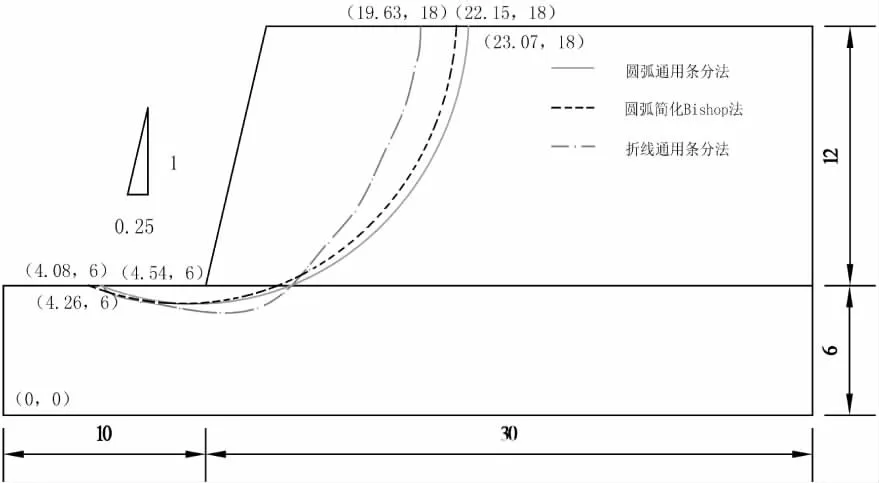
图4 算例1临界滑动面计算结果(单位：m)

由上述计算结果可知，初始滑动面设置为圆弧滑动面时，简化Bishop法与通用条分法计算得到的安全系数和临界滑动面位置基本相同；与圆弧滑动面相比，折线滑动面得到的安全系数偏小，原因在于折线滑动面没有规定具体的滑动面形状，在搜索过程中可以找到更为多样的潜在滑动面，这与文献[16]的研究结果是相同的．

为了验证上述结果的合理性和可行性，进而给出下列两种算例进行分析．

2.2 加筋边坡

2.2.1 基本计算模型及参数

算例2为一土工格栅加筋边坡，即在算例1的基础上增加拉筋带，筋材长度为12 m，基本计算模型尺寸如图5所示，土体参数与算例1相同(见表1)．筋材的抗拉屈服强度为80 kN/m，计算分析中将筋材简化为力增加到土条的力与力矩平衡分析中，计算方法详见文献[17]．

图5 算例2计算模型(单位：m)

2.2.2 结果分析

经分析计算后，得到的安全系数及其相应临界滑动面(见表3和图6)．

表3 算例2安全系数计算结果

图6 算例2临界滑动面计算结果(单位：m)

由算例2的分析结果可知，边坡加筋后的安全系数总体提高，同时也满足在圆弧滑动面下两种算法安全系数和滑动面十分接近；折线滑动面的安全系数比圆弧滑动面小，滑动面有所差别但总体趋势一致．

2.3 成层土非均质边坡

2.3.1 基本计算模型及参数

算例3为延安机场迁建工程的非均质边坡，迁建项目场区处于延安市的东南方，地处宝塔区柳林镇，离市中心约15 km．整体而言，该区西北向偏低，东南向偏高，场区的山体大多被冲沟冲刷为形状各异的侵蚀和剥蚀黄土峁与黄土梁，起伏不平，深切绵延．工程现场的山梁和山峁宽从250 m到450 m不等，梁顶和峁顶的地势相对比较平坦，沟谷宽从75 m至300 m之间变化，谷坡陡峭嶙峋，沟谷底部与梁峁顶部相差大约147 m．依据勘测资料和钻探结果，地层从上到下顺次是植物层、坡洪积粉质黏土、第四系上更新统风积黄土、残积古土壤、中更新统风积黄土和残积古土壤．具体土层划分及基本计算模型尺寸如图7所示，土体参数见表4．

图7 算例3计算模型(单位：m)

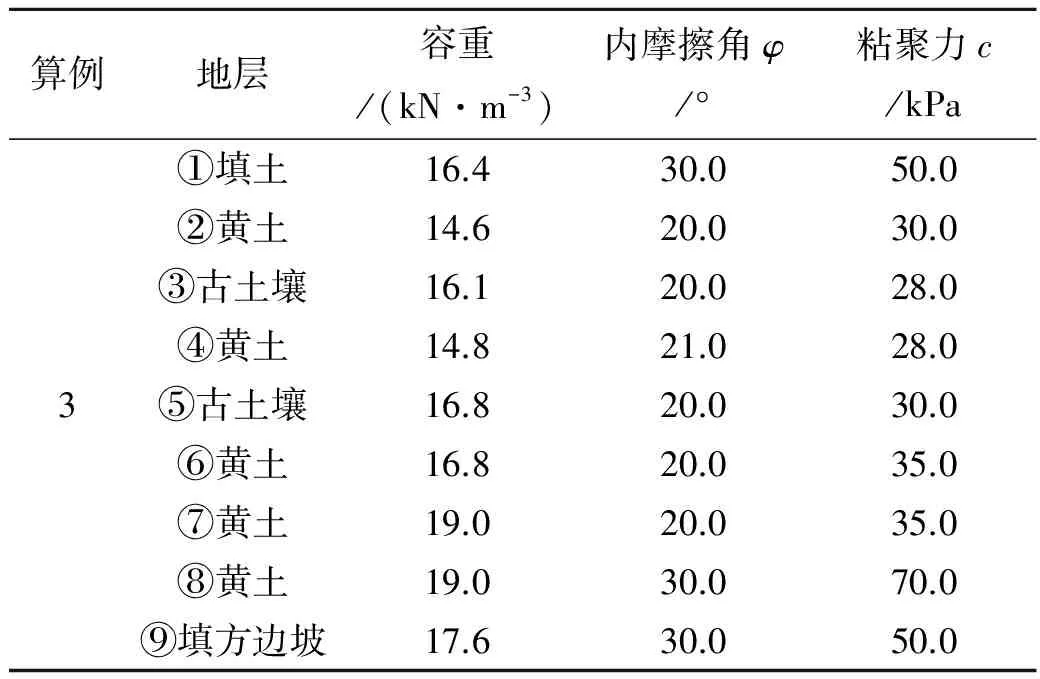
算例地层容重/(kN·m-3)内摩擦角φ/°粘聚力c/kPa3①填土16．430．050．0②黄土14．620．030．0③古土壤16．120．028．0④黄土14．821．028．0⑤古土壤16．820．030．0⑥黄土16．820．035．0⑦黄土19．020．035．0⑧黄土19．030．070．0⑨填方边坡17．630．050．0

2.3.2 结果分析

经分析计算后，得到的安全系数及其相应临界滑动面(见表5和图8)．

表5 算例3安全系数计算结果

图8 算例3临界滑动面计算结果(单位：m)

算例3依旧保留上述结果分析的规律，但折线滑动面与圆弧滑动面计算得到的安全系数相差较大，其主要原因是，由于折线滑动面和圆弧临界滑动面的搜索方法不同，在成层土的情况下，折线和圆弧的临界滑动面差异较大，因此其安全系数差别较大．说明当土体介质较为复杂时，圆弧滑动面在搜索过程中容易陷入局部极值，而折线滑动面容易搜索到全局极值．

3 结 论

1)通过算例对比分析，当滑动面为圆弧滑动面时，简化Bishop法与通用条分法计算得到的安全系数和临界滑动面位置基本相同．

2)不同初始滑动面形式下得到的临界滑动面有一定的差异，但总体趋势相接近；对于几何形状复杂的非均质边坡而言，只有初始滑动面充分接近全局临界滑动面时，搜索过程中才不易陷入局部极值．

3)由于折线滑动面没有规定具体的滑动面形状，因此可以搜索到更为多样和合理的滑动面，故其安全系数比圆弧滑动面方法计算的小，对于均质土坡，折线滑动面与圆弧滑动面的安全系数和临界滑动面相差不大，但对于加筋边坡与非均质边坡，两者有一定的差别，此时应用折线滑动面更容易搜索到全局极值．

[1] 李领先．基于极限平衡法的边坡稳定性计算[J]．科技信息，2009(12)：614-615．

[2] 苏利军．基于极限平衡法和有限元法的土质边坡稳定分析研究[D]．成都：西华大学，2012．

[3] 卢坤林，朱大勇，甘文宁，等．一种边坡稳定性分析的三维极限平衡法及应用[J]．岩土工程学报，2013，35(12)：2276-2282．

[4] 白 桃，黄晓明．考虑土体参数空间变异性的边坡极限平衡法求解[J]．西南交通大学学报，2014，49(4)：662-667．

[5] 王 旭，刘东升，宋强辉，等．基于极限平衡法的边坡稳定性可靠度分析[J]．地下空间与工程学报，2016，12(3)：839-844．

[6] 邓东平，李 亮．基于滑动面应力假设下的三维边坡稳定性极限平衡法研究[J]．岩土力学，2017，38(1)：189-196．

[7] 代凌辉，张 胤，李 建．抗滑桩在加固边坡稳定性中的应用及影响分析[J]．水利水电技术，2016，47(12)：52-55，65．

[8] 刘金龙，陈陆望，王吉利．边坡稳定性分析方法简述[J]．水电能源科学，2008(1)：133-137．

[9] 崔 蕾．简化毕肖普法在不同安全系数体系下应用的对比分析[J]．赤峰学院学报：自然科学版，2008，24(5)：105-108．

[10] Fredlund D G, Krahn J． Comparison of Slope Stability Methods of Analysis[J]． Canadian geotechnical journal， 1977, 14(3)：429-439．

[11] Chugh A K． Variable Interslice Force Inclination in Slope Stability Analysis[J]． Soils and foundations, 2008, 26(1)： 115-121．

[12] 张鲁渝．一个用于边坡稳定分析的通用条分法[J]．岩石力学与工程学报，2005，24(3)：496-501．

[13] 张鲁渝．边坡稳定分析软件ZSlope的开发[J]．岩石力学与工程学报，2004，23(16)：2830-2835．

[14] 张鲁渝，张建民．基于MonteCarlo技术的临界滑面搜索算法的实现及改进[J]．岩土工程学报，2006,28(7)：857-862．

[15] 张鲁渝，张建民．基于滑面段旋转的Monte Carlo搜索技术及改进(I)：转角大小随机[J]．岩土力学，2006,27(11)：1902-1908．

[16] 张鲁渝，张建民．基于滑面段旋转的Monte Carlo搜索技术及改进(Ⅱ)：常值转角[J]．岩土力学，2006,27(12)：2197-2202．

[17] 肖 杰，吴 宏，张锦涛．折线型滑裂面边坡的稳定性问题研究[J]．工程与试验，2015，55(3)：26-29．

[18] Song F, Chen R Y, Ma L Q, et al． A New Method for the Stability Analysis of Geosynthetics-reinforced Slopes[J]． Journal of mountain sciences, 2016, 13(11)：2069-2078．

ComparisonbetweenArcandPolylineFailureSurfacesinSlopeStabilityAnalysis

Li Jianju1Li Yuying2

(1. The 9th General Team of Airport Construction of China, Chengdu 611430, China; 2. School of Highway Engineering, Chang'an University, Xi'an 710064, China)

In this paper, the effects of two kinds of sliding surfaces of arc and polyline and simplified Bishop method and generalized limit equilibrium method (GLE) for slope stability analysis are studied.Taking the homogeneous slope, the reinforced slope and the stratified soil heterogeneous slope as examples, the circular and polyline sliding surfaces are calculated by two algorithms to analyze the difference between the safety factor and the critical slip surface. The results show that when the sliding surface is an arc sliding surface, the simplified Bishop method and the generalized limit equilibrium method have the same safety factor and critical slip surface. Compared with the arc sliding surface, the safety factor obtained by the polyline sliding surface is smaller. It is shown that the arc is easy to fall into local extremum for complex slopes; while the polyline sliding surface is easy to search for global extremum. The study results can provide theoretical references for the design of engineering slopes.

slope stability; arc sliding surface; polyline sliding surface; factor of safety; general limit equilibrium method

10.13393/j.cnki.issn.1672-948X.2017.05.004

2017-08-08

住房与城乡建设部研究开发项目(2015-K2-008)

李建举(1962-)，男，高级工程师，硕士研究生，研究方向为机场工程及管理．E-mail：Lijj1962@outlook.com

TU43

A

1672-948X(2017)05-0017-05

[责任编辑周文凯]

土木水电论坛栏目征文

《三峡大学学报(自然科学版)》是科技部中国科技论文统计源期刊和俄罗斯《文摘杂志》、美国《化学文摘》、英国《INSPEC》收录期刊，并已加入《中国学术期刊(光盘版)》和“中国期刊网”，在水利电力行业有一定的影响力和知名度。本刊自2004年开设了“水电论坛”栏目(现更名为“土木水电论坛”)，主要刊载反映国内外土木水电建设中的最新科研成果和工程应用的论文。欢迎土木水电工程科研和建设单位的广大作者踊跃投稿，我们将以最大的热情和最快的速度为您服务。对您所投的“土木水电”类论文，属省、部级以上基金资助的，我刊将免收版面费，且稿酬从优！