提升数学阅读能力的命题与教学*
朱昌宝
提升数学阅读能力的命题与教学*
朱昌宝
数学阅读理解题有助于考查评价学生的综合学习能力,它需要学生具备洞察力、理解力和执行力,此类题成为当下数学命题的宠儿。数学阅读理解命题应以能力立意,以素养为本,通过科学的命题来促进学生数学阅读能力的提升。
数学阅读;初中数学;命题
《义务教育数学课程标准(2011年版)》在合理设计与实施书面测验中提出:“为考查学生从具体情境中获取信息的能力,可以设计阅读分析的问题。”数学阅读理解题成为中考命题的宠儿。纵观近几年的数学中考试卷,这类试题主要有以下几种类型:阅读解题过程,总结解题的思路和方法;阅读基本模型,研究模型运用;阅读特殊范例,推出一般性结论;阅读新定义,研究新应用。笔者试从教学与命题的角度对其进行分析。
一、数学阅读能力的要素
戏有戏眼,题有题眼。对数学阅读题中可有可无的文字,我们可以“快刀斩乱麻”,去伪存真,筛选出有关键作用的题眼。学生以题眼为纽带,激活大脑中与之相关的各种信息,对思维障碍进行精确“打击”。
2.关键句的解读能力。
关键句的解读能力是基于关键词的理解以及原有知识的认知结构,根据全句的含义,快速破解出与之等价的数学结论或数学模型。如此一来,学生的思维就会如汩汩泉水般涌流不断。
3.图象的甄别能力。
图象是数学题目的重要载体,数形结合思想是初中数学重要的思想方法之一。图象的甄别能力是读图的基本要求,一般通过图象的起点、交点、转折点、对应点、终点来获取原始的信息,通过纵向对比掌握变化规律,通过横向对比寻找互相的联系,最终找到解决问题的方法。
4.信息的综合能力。
(1)支持性心理治疗。信息支持,评估患者相关知识需求,介绍冠心病及PCI相关知识,告诉其可能出现的并发症及预防措施;情感支持,以热情诚恳的态度关心体贴患者,取得患者的信任与合作,每天至少和患者交谈10分钟,以建立良好的护患关系;社会支持,促进患者健全社会支持网络,充分利用社会支持系统,从家庭成员、亲朋好友及医护人员、病友三方面给予其广泛的社会支持。
阅读材料中的每一处信息都可能与其他信息构成某种“超结构”的逻辑关系,作为关联方的“其他信息”,可以同在题目中,也可以在阅读者的知识结构中。信息综合就是发现阅读内容所涉及的、游离于题目之外的各种逻辑关系。没有信息综合,就不会有批评性思维,也不会有全面系统的图式架构,更不会有举一反三、触类旁通的知识迁移。
二、基于数学阅读能力提升的阅读理解题命制
1.把握时代命脉,拓宽数学阅读视域。
数学离不开生活,生活处处是数学。数学阅读理解题融入生活元素,紧跟时代的步伐,这样的题目有新意,让人耳目一新。
例如2016年湖南长沙卷第25题,若抛物线L:y=ax2+bx+c(a,b,c 是常数,abc≠0)与直线 l都经过y轴上的一点P,且抛物线L的顶点Q在直线l上,则称此直线l与抛物线L具有 “一带一路”关系,此时,直线l叫作抛物线L的“带线”,抛物线L叫作直线l的“路线”。(1)若直线y=mx+1与抛物线y=x2-2x+n具有“一带一路”关系,求m、n的值;(2)若某“路线”L的顶点在反比例函数y=的图象上,它的“带线”l的解析式y=2x-4,求此“路线”L的解析式;(3)当常数满足时,求抛物线 L∶y=ax2+(3k2-2k+1)x+k 的 “带线”l与 x轴、y轴所围成的三角形面积的取值范围。
“一带一路”是“丝绸之路经济带”和“21世纪海上丝绸之路”的简称,是国家级顶层战略,对中国的经济发展起着举足轻重的作用。题目借助这一名词,给出“一带一路”新定义,洋溢着强烈的时代信息,有利于改变学生“两耳不闻窗外事,一心只读圣贤书”的习惯。学生解题时应抓住“一带一路”中的“带线”“路线”,解析式之间的内在关系(常数项相同,前者一次项系数是后者一次项系数的一半),化抽象为直观,数形结合,最终求得结果。类似的题目还有2014年四川巴中卷出现的“杨辉三角”阅读理解题、2015年四川资阳卷的“梦之星”阅读理解题、2016年山西卷的“菱形纸片的剪拼”阅读理解题等。
2.强化基本元素,提升数学阅读能力。
初中数学教材中蕴涵着丰富的数学基本知识、常见的数学思想方法和数学的基本模型。数学阅读题借助这些基本元素,由浅入深地设计一些与之相关的问题串,可以达到一题多用的功效,对培养学生阅读思维的深度和广度有着较好的作用。
例如2017年南通启东二模第27题,定义:对于线段MN和点P,当PM=PN,且∠MPN≤120°时,称点P为线段MN的 “等距点”。特别地,当PM=PN,且∠MPN=120°时,称点P为线段MN的“强等距点”。如图1,在平面直角坐标系xOy中,点A的坐标为
(1)若点B是线段OA的“强等距点”,且在第一象限,则点B的坐标为______;
(2)若点 C是线段OA的“等距点”,则点 C的纵坐标t的取值范围是______;
(3)将射线OA绕点O顺时针旋转30°得到射线l,如图2所示。已知点D在射线上,点E在第四象限,且点E既是线段OA的“等距点”,又是线段OD的“强等距点”,求点D的坐标。
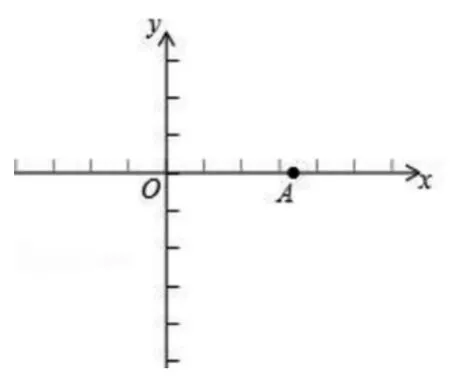
图1
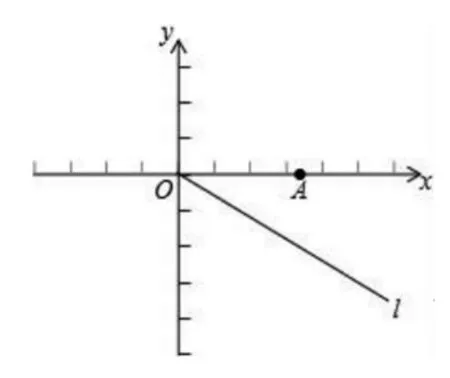
图2
该题以基本知识(等腰三角形的性质、中垂线的性质)、基本图形(平面直角坐标系、等腰三角形)、基本数学思想(数学结合、分类讨论)为抓手,考查了学生运用现有知识和技能探究新情境、解决新问题的能力,符合“最近发展区”理论,培养了学生的应用意识、创新意识。类似的还有2016年重庆卷的“最佳分解”、2016年浙江衢州卷的“垂美四边形”、2016年辽宁大连卷的“线段倍数关系”的阅读理解题。
3.立足知识衔接,夯实数学阅读基础。
中考既是毕业考试,又是为高中输送人才的选拔考试。为了试题具备一定的区分度,命题者往往将高中的知识作为数学阅读题的阅读内容,考查学生利用已有知识和解题经验进行灵活应变的能力。通过挖掘一些新定义的本质加深对新概念的理解与运用,为高中数学的学习做铺垫,为有效培养学生阅读思维的深刻性打下坚实的基础。
例如2016年北京市海淀区初三期末试题:如图3,在平面直角坐标系xOy中,定义直线x=m与双曲线的交点 Am,n(m、n 为正整数)为“双曲格点”,双曲线在第一象限内的部分沿着竖直方向平移或以平行于轴的直线为对称轴进行翻折之后得到的函数图象为其“派生曲线”。
(1)①“双曲格点”A2,1的坐标为______;②若线段 A4,3A4,n的长为 1 个单位长度,则 n=_____;

图3
本题重点考查函数图象及其变换,这是高中研究函数的重要方法,解题过程中体现出浓厚的数形结合思想,更重要的是在数学思想方法上体现初高中数学知识的衔接,借助双曲线的“派生曲线”考查函数图象、函数图象的变换,使学生做一题,会一类,最终收获满满。类似的试题有2015年浙江衢州卷的“旋转函数”、2015年浙江宁波卷的“智慧角”、2012年北京卷的“非常距离”等。
三、基于提升数学阅读能力的命题
数学阅读理解题命题的环节与步骤较多,需要深思熟虑,不宜一气呵成。命题者需要立足于提升学生的数学阅读能力进行命题,具体而言有如下几点。
1.宏观上对准“面”。
在着手数学阅读命题前,命题者需要明确以下两点——
首先,不可让阅读理解题像解答题那样侧重基本能力考查。为了保证阅读理解题应有的区分度,也为了考查出学生在数学阅读能力方面的差异,阅读理解题的命题应该有自身的目标,即考查学生在阅读时是否能够捕捉相应的信息,记住并使之在记忆中保持活跃,所以阅读理解题对学生的迅即反应和短时记忆能力的要求较高。
其次,要避免考察面过窄。数学阅读题提供的阅读材料应该为学生全面展示应有的阅读能力提供充足空间,教师设计的问题应尽可能多地覆盖文本的解读成果。换言之,文本材料对各种阅读能力的覆盖率、题目设计对阅读目标的覆盖率都应该遵循宜高不宜低的原则,否则就不能准确反映学生阅读思维能力的差异。
2.中观上布好“线”。
目前的数学阅读题基本均由填空、解答、证明等多种形式组成,这几种题型都是学生阅读能力水平的控制线。命题者一方面要确定某种类型题应该淘汰哪一种水平的学生,进而将所有题目的水平控制线规划出合理梯度;另一方面还须为这些“线”赋予不同方面或层次上的属性特征,避免几种类型的问题处于同一水平。另外,整个阅读理解题应该有一条主线贯穿其中,如上例中的“一带一路”“派生曲线”等。
3.微观上整合“点”。
阅读理解的问题都应该与阅读内容息息相关,学生围绕考查的知识点而展开的答题思维应该集中在同一个主题空间之中,设计的问题应循序渐进、拾阶而上。不同问题的难度设置要适当且合理,这样有利于学生有的放矢,以点带面,各个击破。
聚焦于提升阅读能力的数学阅读理解命题,实际上是数学教师基于学生的认知规律和能力水平,在假想中与答题中进行的思维活动。一道好的阅读题,需要命题者精心打磨与统筹,这样的题目才能彰显其应有的价值要义,更好地推动学生数学阅读能力的提升。
[1]林志诚.基于考查学生“学习能力”的命题方式——福建省漳州市中考“阅读分析题”命题感悟[J].中国数学教育:初中,2016(11).
[2]刘旭亮.“一带一路”新定义 数形结合现本质[J].中学数学教学参考,2016(23).
G633.6
A
1005-6009(2017)75-0045-03
朱昌宝,江苏省南通市通州区平潮实验初中(江苏南通,226361)教师,高级教师,南通市学科带头人。
*本文系江苏省教育科学“十二五”规划2011年度初中专项课题“农村初中生数学阅读力培养的实践研究”(课题编号:E-c/2011/52)的研究成果。

