2017年高考“数学文化类”试题赏析
山东 尹承利
2017年高考“数学文化类”试题赏析
山东 尹承利
2017年高考在万众瞩目下落下了帷幕,在高考试题中渗透数学文化成为今年数学高考的一大亮点,全国的一、二卷和高考改革地区的浙江卷都做了有益的尝试和探索,体现了高考“增加数学文化”的要求.先睹为快,笔者就2017年高考中的数学文化类试题特点予以梳理并赏析,与诸位同仁分享.
一、以古代数学名题为题源
【例1】(2017·全国卷Ⅱ理3)我国古代数学名著《算法统宗》中有如下问题:“远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”意思是:一座7层塔共挂了381盏灯,且相邻两层中的下一层灯数是上一层灯数的2倍,则塔的顶层共有灯
( )
A.1盏 B.3盏
C.5盏 D.9盏
【解析】可设最顶层灯塔所挂灯数为a,则第二层为2a,第三层为4a,……,第七层为64a,所以本题实质是考查等比数列求和公式,故127a=381,可得a=3,故选B.
【点评】我国古代数学有着极其辉煌的成就,出现过像刘徽、祖冲之、秦九韶、杨辉等伟大的数学家,以及《九章算术》、《数书九章》、《算数书》、祖暅原理等数学名著、名题,以这些名著、名题为试题背景,可以引导我们理解数学,感受数学家的崇高品质以及探究、解决数学问题的过程,进而体会中国古代数学的伟大贡献,增强爱国主义情怀.程大位是我国明代伟大的数学家,被誉为“珠算之父”,他的应用数学巨著《算法统宗》的问世,标志着我国的算法由筹算到珠算转变的完成.程大位在《算法统宗》中常以诗歌的形式呈现数学问题,体现了数学的“文化美”.
尤其指出是:2017年《教学考试》数学第1期题组变式训练(二)《数列与推理》第4题押中了该高考题,说明了《教学考试》(数学)在研究高考命题规律方面具备很深的造诣.
【变式1】我国古代数学名著《算法统宗》中有一首叫“宝塔装灯”的诗,内容为“远望巍巍塔七层,红灯点点倍加增,共灯三百八十一,请问尖头几盏灯?”(“倍加增”指灯的数量从塔的顶层到底层按公比为2的等比数列递增),根据此诗,可以得出塔的顶层和底层共有
( )
A.3盏灯 B.192盏灯
C.195盏灯 D.200盏灯

【变式2】我国古代数学名著《算法统宗》中有一道“竹筒容米”问题:“家有九节竹一茎,为因盛米不均平,下头三节三升九,上梢四节贮三升,唯有中间二节竹,要将米数次第盛,若有先生能算法,也教算得到天明.”([注释]三升九:3.9升.次第盛:盛米容积依次相差同一数量.)用你所学的数学知识求得中间两节的容积为
( )
A.1.9升 B.2.1升
C.2.2升 D.2.3升

二、以古代著名方法为背景命题
【例2】(2017·浙江11)我国古代数学家刘徽创立的“割圆术”可以估算圆周率π,理论上能把π的值计算到任意精度.祖冲之继承并发展了“割圆术”,将π的值精确到小数点后七位,其结果领先世界一千多年.“割圆术”的第一步是计算单位圆内接正六边形的面积S6,S6=________.
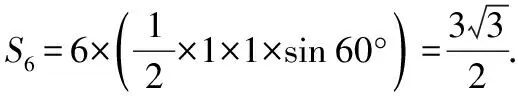
【点评】说到圆周率π,自然想到我们引以为豪的“徽率”和“祖率”,它的历史饶有趣味.我国古代数学家对圆周率方面的研究工作,成绩十分地突出.本题所介绍的祖冲之研究圆周率π的成果,使我们感到无比的自豪和骄傲.古代科学家在艰难的环境中研究科学的精神和崇高品质,是值得我们尊敬和学习的.
【变式3】割圆术是我国古代数学家刘徽创造的一种求周长和面积的方法:随着圆内接正多边形边数的增加,它的周长和面积越来越接近圆周长和圆面积,“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣”.试用这个方法解决问题:如图,⊙O的内接多边形周长为3,⊙O的外切多边形周长为3.9,则下列各数中与此圆的周长最接近的是
( )



【解析】圆外切多边形的周长大于圆周长,圆内接多边形的周长小于圆周长.圆的内接多边形周长为3,外切多边形周长为3.9,所以圆周长在3与3.9之间.只有C选项满足条件.故选C.
三、以古代经典图形为背景命题
【例3】(2017·全国卷Ⅰ文4、理2)如图,正方形ABCD内的图形来自中国古代的太极图.正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称.在正方形内随机取一点,则此点取自黑色部分的概率是
( )



【点评】我国传统文化中很多内容体现了数学的“对称美”.如图所示的太极图是由黑白两个鱼形纹组成的圆形图案,充分体现了相互转化、对称统一的形式美、和谐美.
【变式4】大衍数列来源于《乾坤谱》中对易传“大衍之数五十”的推论.主要用于解释中国传统文化中的太极衍生原理.数列中的每一项,都代表太极衍生过程中,曾经经历过的两仪数量总和.是中华传统文化中隐藏着的世界数学史上第一道数列题.其前10项依次是0,2,4,8,12,18,24,32,40,50,…,则此数列第20项为
( )
A.180 B.200
C.128 D.162
【答案】B
【变式5】给出定义:能够将圆O的周长和面积同时平分的函数称为这个圆的“优美函数”.给出下列命题:
①对于任意一个圆O,其“优美函数”有无数个;

③正弦函数y=sinx可以同时是无数个圆的“优美函数”;
④函数y=f(x)是“优美函数”的充要条件为函数y=f(x)的图象是中心对称图形.
其中正确的有
( )
A.①③ B.①③④
C.②③ D.①④
【答案】A
四、推理论证常考常新
【例4】(2017·全国卷Ⅱ文9、理7)甲、乙、丙、丁四位同学一起去向老师询问成语竞赛的成绩,老师说:你们四人中有2位优秀,2位良好,我现在给甲看乙、丙的成绩,给乙看丙的成绩,给丁看甲的成绩.看后甲对大家说:我还是不知道我的成绩,根据以上信息,则
( )
A.乙可以知道四人的成绩
B.丁可以知道四人的成绩
C.乙、丁可以知道对方的成绩
D.乙、丁可以知道自己的成绩
【解析】由甲说不知道自己成绩且看过乙和丙的成绩,可推出乙和丙一优一良,又因为乙看过丙的成绩,所以乙可以推测出自己的成绩,因为已经推出乙和丙一优一良,所以甲和丁也是一优一良,并且条件已给出丁看过甲的成绩,所以丁也可以推测出自己成绩,故选D.
【点评】推理论证问题是近几年高考中常考常新的重要题型,2014年高考全国卷Ⅰ文、理14题曾做过考查,今年卷Ⅱ又再一次考查到.以逻辑推理问题命制高考题,既能创造宽松又竞争的环境,拉近考生与数学的心理距离,又能考查学生的阅读理解能力和逻辑推理能力.乍看这类问题,高中所学的知识好像在此全无用武之地,练就百遍的解题技巧似乎也在此搁浅,然而数学思维能力,却在此大放光彩.
【变式6】在一个俱乐部里,有老实人和骗子两类成员,老实人永远说真话,骗子永远说假话.一次我们和俱乐部的四个成员谈天,我们便问他们:“你们是什么人,是老实人?还是骗子?”这四个人的回答如下:
第一个人说:“我们四个人全都是骗子”.
第二个人说:“我们当中只有一个人是骗子”.
第三个人说:“我们四个人中有两个人是骗子”.
第四个人说:“我是老实人”.
请判断一下,第四个人是老实人吗?________.(请用“是”或“否”作答)
【解析】(1)四个人当中一定有老实人,因为如果四个人都是骗子,则谁也不会说“我们四个人全都是骗子”,所以第一个人是骗子.
(2)第二个人为骗子,因为他如果是老实人,由于已经判断了第一个人是骗子,则第二,三,四个人都是老实人.但第三个人的回答与他矛盾,两个人不可能是同类的,故第二个人说的是假话,他是骗子.

山东省泰安英雄山中学)

