一种相控阵天线REV幅相校正方法的仿真与实践

，，

(1.北京空间飞行器总体设计部，北京 100094; 2.北京市电磁兼容与天线测试工程技术研究中心，北京 100094

一种相控阵天线REV幅相校正方法的仿真与实践

张橹1，杜海龙2，卢铮1

(1.北京空间飞行器总体设计部，北京100094; 2.北京市电磁兼容与天线测试工程技术研究中心，北京100094

介绍了基于傅里叶分析的旋转矢量算法(REV)，并将该算法应用于相控阵天线各单元的初始幅相误差校正，给出了它的仿真分析和工程实现方法;所使用的校正方法区别于以往采用的REV校正方法，利于减少校正天线对相控阵收发信号的影响;仿真结果显示，校正后各通道的相位和幅度与人为设置的相位、幅度只差一个常数，表明方法是有效的；通过实际测试，校正后的天线方向图与近场校正结果逼近，EIRP比校正前提高1.4 dB以上，验证了校正方法的功能和性能。

相控阵天线；幅相校正；傅里叶分析；旋转矩量法

0 引言

相控阵天线的性能依赖各个阵元的相对相位和位置。由于射频通道的幅度相位存在误差，各个阵元工作时的幅度和相位关系与期望值有差别，使波束变形，性能恶化[1,2,3]。因此，需要检测相控阵单元的初始幅相误差。文献[4]提出的旋转矢量(REV,rotating-element electric-field vector)校正方法，可以检测出这种相控阵单元通道的幅度和相位误差。

然而，现有的文献均未能给出该算法的具体实现方法。因此，本文在研究基于傅里叶分析的旋转矢量方法的基础[5]上，给出了基于REV算法相控阵天线幅相校正的实现方法。该方法区别与以往采用的REV校正方法，可以减少校正天线对相控阵收发信号的影响。基于所给的工程实现方法，开展了系统仿真和实物测试。通过仿真，验证了所给出的幅相校正方法的正确性；通过实际测试，验证了其校正和监测功能。根据实测结果，得出一些有益结论。

1 基于傅里叶分析的旋转矢量(REV)校正方法

旋转矢量法是一种检测相控阵各单元通道幅度和相位误差的方法，该方法对发射阵和接收阵都适用[6]。图1是旋转矢量法校正系统组成，这种方法通过依次改变被校正单元的移相器的值，测量相应电场矢量幅度的变化值，就可以计算出该单元天线的幅度和相位值。

图1 旋转矢量法校正系统组成

如图2所示，旋转矢量法考虑两个复信号A1exp(jØ1)和A2exp(jØ2)，它们的和信号记为Eexp(jØ)。其中，是A2exp(jØ2)旋转单元的信号，A1exp(jØ1)是其他阵元的信号之和。利用移相器对A2exp(jØ2)引入额外相移Δ。

图2 合成电场矢量和单元天线电场矢量

将Δ从0依次变化到2π，记录E的最大值、最小值，以及使E达到最大时移时所引入的相移增量Δ，可以计算出A1，A2和Ø2-Ø1。但是对于广泛使用的数字移相器，只能提供离散的相位状态，不能准确知道Δ。文献[5]使用傅立叶分析的方法 , 求解旋转矢量法中的固定信号分量和旋转信号分量 , 提高了计算速度和精度。

当移相器为n位数字移相器时，移相器只能提供N=2n个相位状态。其相位分辨率为δ=2π/N，当移相器从状态0变化到状态N-1，完成一个周期的变化，测得的信号序列功率为E2(iδ),i=0,1,…N-1。当移相器为第i个相位状态时，Δ=iδ有:

E2(iδ) =A12+A22+ 2A1A2cos(∅2-∅1+iδ)

i=0,1,2,3…M-1

(1)

为测量得到的移相器在不同相位状态时的功率序列。

令：

(2)

(3)

(4)

可计算得出：

(5)

令

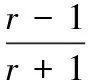
(6)

可得，校正单元的相对相位X为

(7)

式中，X的单位为角度。应根据Г+cosΔ的符号对所求的X进行修正[7]。由此可以补偿相控阵单元的初始相位误差。校正单元的幅度K为

(8)

2 基于傅里叶分析的旋转矢量(REV)校正仿真

构建一个二维矩形相控阵天线模型，对所给出的REV校正方法的效果进行仿真，相控阵天线模型如图3所示。在仿真过程中，选取阵列中位置较为典型的13个通道，均匀的分布在天线阵面上，并且覆盖了阵面中心和边缘的各个不同位置，图中以实心圆点表示。

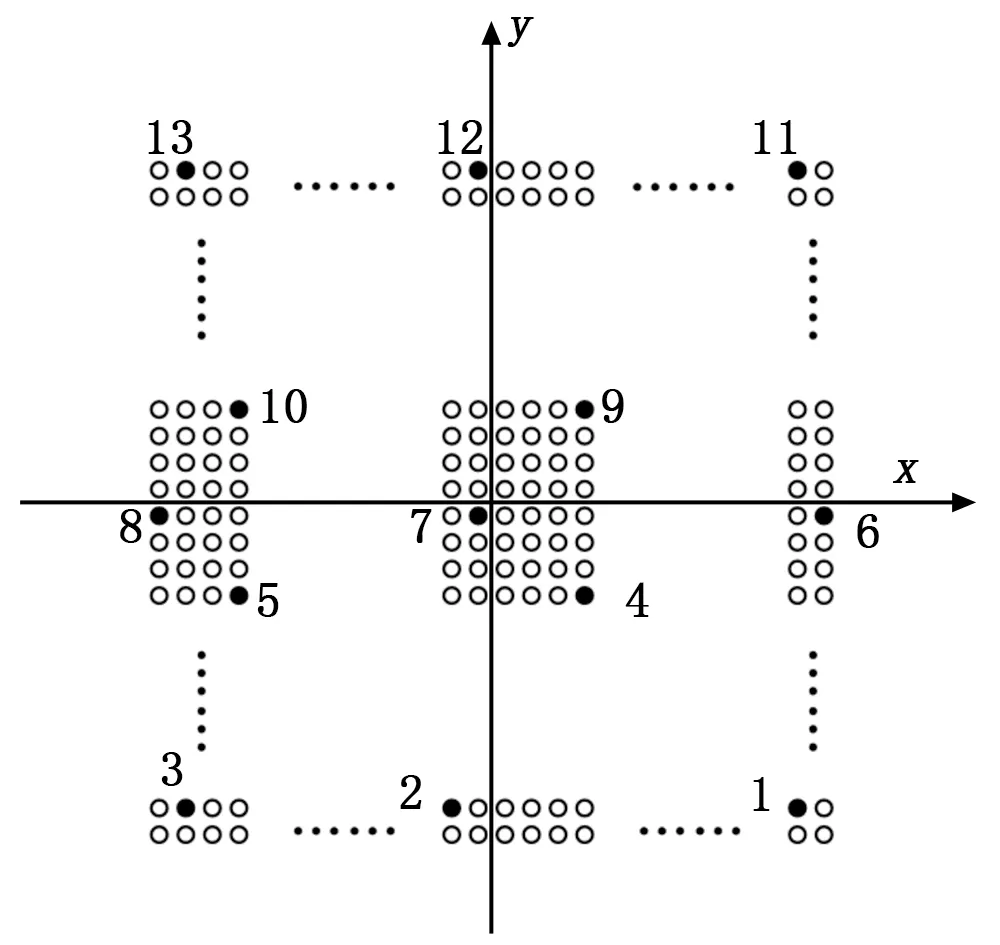
图3 用于仿真的相控阵天线阵面布局图

幅相校正性能表现在两个层次上，一是体现在系统指标的层面如相控阵的EIRP、G/T，副瓣电平和指向误差等指标；另一个层次是通道间的幅相误差。幅相校正的性能本质上是体现在通道间的幅相误差上，通道间的幅相误差得到修正后，系统指标自然而然会得到修正，反之系统指标自然会恶化。

使用MATLAB对幅相校正算法的性能进行仿真，仿真的主要步骤包括：1)在MATLAB中构建一个二维矩形相控阵天线模型；2)在模型中选取位置较为典型的13个通道，均匀的分布在天线阵面上，且覆盖了阵面中心和边缘的各个不同位置；3)对选取的13个通道设置各自的初始幅度与相位，理想状态下，各个通道应具有相同的幅度与相位特性，因此此处将各个通道的初始幅度与相位均设为“0”；4)当相控阵天线各通道性能发生变化时，其初始幅度与相位特性也将发生变化，因此在选取的13个通道上叠加一个随机的相位误差和幅度误差；5)在MATLAB环境下运行幅相校正算法，对所选13个通道的幅度与相位进行校正，并得到校正后的幅度与相位修正量；6)校正后的幅度与相位修正量与步骤4)中所设置的随机幅度误差与相位误差进行比较，得到叠加了幅度与相位修正量后各个通道之间的幅度与相位误差；7)对步骤6)的结果进行分析，评估幅相校正算法的性能。

2.1 幅相校正仿真结果

幅相校正仿真在通道间幅相误差的层面进行，针对选取的13个通道，首先在相控阵等幅同相的状态下，对全部的辐射单元设置随机的±65°范围内的相位误差，针对选取的13个通道设置幅度误差，然后通过校正计算出在通道间存在幅相误差情况下的相位、幅度，该相位、幅度与设置相位、设置幅度的差值，即可表征修正后通道间的幅相误差，并可间接的反映幅相校正的性能。

等幅同相状态和存在幅相误差状态的原始数据分别见图4和图5，从图中可以看出，通过设置随机相位误差以及幅度误差后，选取通道在不同移相状态下的幅度均发生了明显的变化。

图4 等幅同相状态校正仿真原始数据

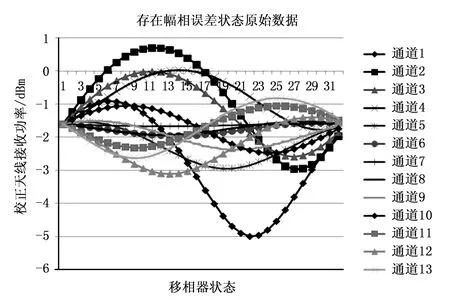
图5 设置幅相误差后的仿真原始数据

通过校正仿真计算的结果如表1所示，从表中可以看出，选取的13个通道校正后的相位修正量与设置的初始相位的差值在-53.67°～-53.69°之间变化，各通道间的相位差值变化小于0.02°；13个通道校正后的幅度修正量与设置的初始幅度的差值均为3.21 dB，各通道间的幅度差值为0。由此可知，经过幅相校正后，幅相校正算法补偿了各个通道的初始相位和幅度误差，补偿后各通道间的相位误差小于0.02°，幅度误差为0，表明所使用的幅相校正方法是有效的。

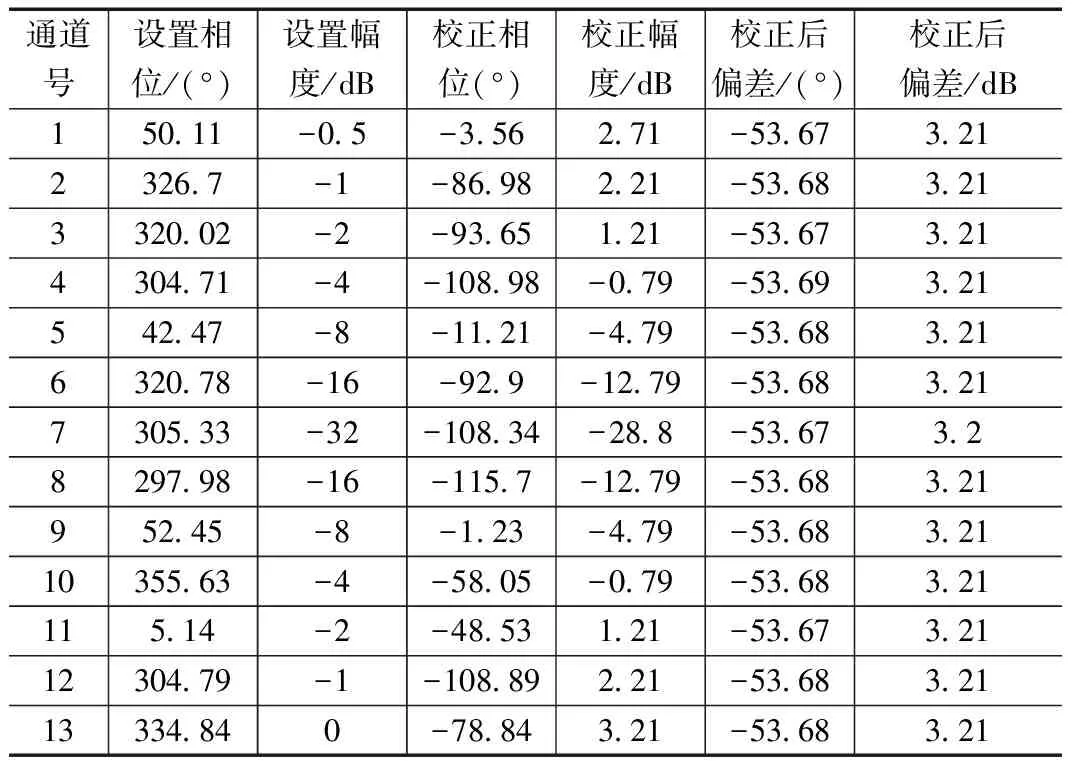
表1 校正仿真计算结果

3 REV校正及测试结果

使用一个二维相控阵天线对REV校正的性能进行验证，幅相校正的测试系统框图如图1所示。验证的主要步骤包括：1)在未进行任何校正补偿的状态下，在微波暗室中测试被测天线的方向图[10-11]和EIRP (Effective Isotropic Radiated Power，有效全向辐射功率)[12-14]；2)在平面近场中对被测天线进行近场校正，得到近场校正后的幅度与相位修正量；3)使用步骤2)中得到的幅度与相位修正量对被测相控阵天线进行幅度和相位补偿，并在微波暗室中测试被测天线的方向图和EIRP，由于近场校正能够有效的补偿相控阵天线各通道间的幅度和相位误差，因此可近似的认为近场校正后的天线方向图和EIRP为理想状态下(各个通道具有相同的幅度和相位特性)相控阵天线的方向图和EIRP；4)在未进行任何校正补偿的状态下，使用图1所示的校正测试系统对被测天线进行幅相校正，得到幅相校正后的幅度与相位修正量；5)使用步骤4)中得到的幅度与相位修正量对被测相控阵天线进行幅度和相位补偿，并在微波暗室中测试被测天线的方向图和EIRP；6)在步骤4)的基础上，使用图1所示的校正测试系统再次对被测天线进行幅相校正，得到幅相校正后的幅度与相位修正量；7)使用步骤6)中得到的幅度与相位修正量对被测相控阵天线进行幅度和相位补偿，并在微波暗室中测试被测天线的方向图和EIRP；8)在步骤6)的基础上，使用图1所示的校正测试系统对被测天线进行第三次幅相校正，得到幅相校正后的幅度与相位修正量；9)使用步骤8)中得到的幅度与相位修正量对被测相控阵天线进行幅度和相位补偿，并在微波暗室中测试被测天线的方向图和EIRP；10)将5次测试得到的方向图和EIRP测试结果进行对比，即可验证幅相校正方法对于天方向图和EIRP性能的改善效果。

3.1 方向图测试

方向图测试数据有5组，分别为初始状态方向图、3次校正后的方向图和近场校正的方向图，如图6所示。每个状态分别测试了对0°，30°，60°扫描的方向图。

图6 相控阵天线正方向图测试结果

表2给出了对应的测试数据。测试数据表明幅相校正后的结果向近场校正的结果逼近，三次校正后的结果差异不大，表明校正是有效的。实际相控阵进行一次校正即可，多次校正不会提高校正效果。

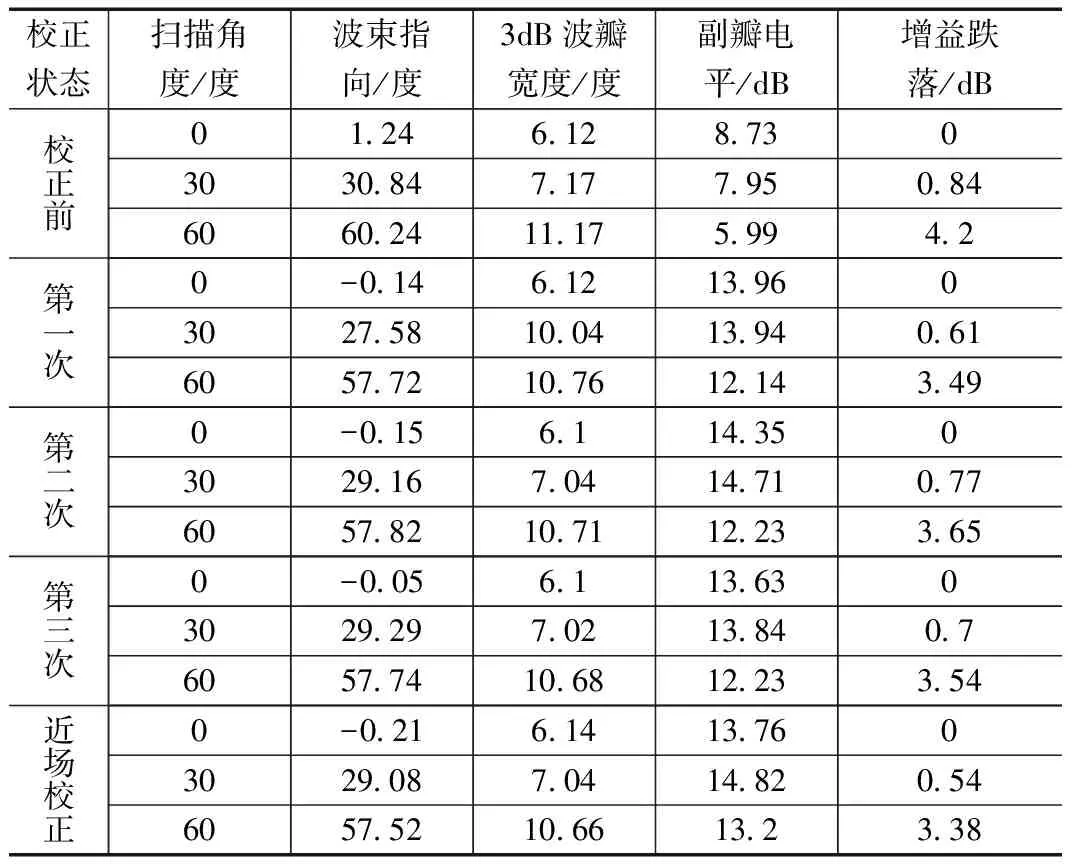
表2 方向图测试结果

3.2 EIRP测试

为了进一步验证校正的效果，分别对校正前、三次校正后和近场校正补偿后进行了EIRP测试。EIRP即有效全向辐射功率，它的定义是天线发送出的功率(P)和该天线增益(G)的乘积，即：EIRP=P*G。如果用dB计算，则为：

EIRP(dBW)=P(dBW)+G(dBW)

(9)

根据测试数据，绘制出了如图7所示的测试曲线。

图7 EIRP测试结果

EIRP测试结果表明，校正前EIRP比近场校正的EIRP低2 dB；校正后，饱和状态下的EIRP比近场校正的EIRP低0.3 dB；P-1点校正后EIRP比近场校正的EIRP低0.6 dB。3次校正后的EIRP非常相近。因此，实际相控阵进行一次校正即可，多次校正不会提高校正效果。测试结果表明校正有效。

4 结束语

本文给出了一种基于REV算法的相控阵天线的幅相校正方法，并给出了它的仿真分析和工程实现方法。仿真结果表明提出的幅相校正方法可以消除相控阵天线各通道间的幅度与相位误差。通过实际的方向图与EIRP测试可知，校正后的方向图与近场校正结果逼近，EIRP比校正前提高1.4 dB以上，进一步验证了校正方法的有效性和实际性能。同时，实测结果表明，多次校正的结果与一次校正相近，因此在实际操作中只需进行一次校正即可。综上，该方法可用于相控阵天线幅相校正的工程实践中。

[1]方 敏. 星载相控阵天线波束校正[D].成都：电子科技大学,2007.

[2] 王 渊. 相控阵天线的幅相误差校正算法及工程实现[D].西安：西安电子科技大学,2013.

[3] 熊 哲. 幅相误差对相控阵天线的性能影响研究[D].中国舰船研究院,2012.

[4]Yonezawa, R; Konishi, Y; Chiba, I;et al.. Beam-shape correction in deployable phased arrays [J].Antennas and Propagation, IEEE Transactions on,1999, 47(3):482-486.

[5]刘明罡,冯正和. 分组旋转矢量法校正大规模相控阵天线[J]. 电波科学学报,2007,03:380-384.

[6]崔卫东,钟 华. 基于旋转矢量法的有源相控阵天线中场测量[J].现代电子技术,2011,15:117-120.

[7]翟 禹,苏东林. 旋转矢量法解的二义性及其消除方法[J]. 北京航空航天大学学报,2012,11:1450-1453.

[8] J J Lee, Edward M Ferren, D Pat Woollen, et al . Near- field probe used as a diagnostic tool to locate defective elements in an array antenna[J] . Antennas and Propagation, IEEE Transactions on,1988, 36( 6) :884- 889.

[9] 熊 旋,王乃彪,焦永昌.一种实用的相控阵近场诊断新方法[J].电波科学学报,2004,19(5):573-576.

[10] 李为玉. 有源相控阵天线发射方向图测试简易方法[J]. 现代电子技术,2012,15:95-96.

[11] 王 侃,王 真. 大型电扫相控阵雷达的天线方向图测试[J]. 现代雷达,2015,08:55-57+64.

[12] 蔡木仁,杨文丽,刘 波,等. 导航卫星在轨EIRP测试方法研究[A]. 第二届中国卫星导航学术年会电子文集[C].中国卫星导航系统管理办公室、科学技术部高新技术发展及产业化司、国防科工局系统工程一司、交通运输部综合规划司、教育部科学技术司、中国卫星导航定位应用管理中心、中国科学院高技术研究与发展局、上海市科学技术委员会,2011:3.

[13] SS Oh, Young-Hwan Lee, Michael Yan Wah Chia. An EIRP Measurement Method for Base-Station Antennas Using Field Strengths Measured along a Single Straight Line[J]. International Journal of Antennas and Propagation,2013.

[14] SS Oh, Woo-Su Kim, Young-Hwan Lee, Ding-Bing Lin. EIRP Characterization of Electrically Large Wireless Equipment with Integrated Signal Generator in a Compact Environment[J]. International Journal of Antennas and Propagation, 2015.

[15] 李 迪. 相控阵天线监测技术研究[D].南京:南京理工大学,2008.

[16] 王晓鹏,赵海明,张远航,等. 基于近场测试的相控阵天线自动化校准与阵面监测方法[J]. 微波学报,2012,S3:229-232.

SimulationandRealizationofREVAmplitudeandPhaseCorrectionforPhasedArrayAntenna

Zhang Lu1, Du Hailong2, Lu Zheng1

(1. Institute of Spacecraft System Engineering, Beijing 100094,China; 2.Beijing Engineering Research Center of EMC and Antenna Test Technology, Beijing 100094,China)

The REV algorithm for correcting the initial amplitude and phase error of the phased array antenna based on Fourier analysis is introduced, and its simulation as well as engineering realization method is given. The given method,which can reduce the interference of the correction antenna to the communication signals, is different from traditional REV method. The simulation result shows that, the amplitude and phase after correction for each element has only a constant difference from the one before correction, which can proof the effection of the given method. Through actual test, the antenna pattern has a good approximation to the pattern after near field correction, the EIRP increased for more than 1.4 dB, compared with the one before REV correction, and the function as well as performance of the given method is verified.

phased array antenna; amplitude and phase correction; Fourier analysis; REV

2017-05-27；

2017-06-20。

张 橹(1983-)，男，福建南平人，硕士，主要从事空间电子信息技术方向的研究。

杜海龙(1974-)，男，内蒙古包头人，博士，主要从事星载相控阵天线技术方向的研究。

卢 铮(1987-)，男，河南信阳人，博士，主要从事空间电子信息技术方向的研究。

1671-4598(2017)09-0254-04

10.16526/j.cnki.11-4762/tp.2017.09.065

TN914

A