锚泊状态下船载测控系统对塔相位标校研究

， ，

(中国卫星海上测控部，江苏 江阴 214434)

锚泊状态下船载测控系统对塔相位标校研究

杨稳竞，吴昊，杨国

(中国卫星海上测控部，江苏江阴214434)

航天器海上测量船是搭载着船载测控系统的海上平台，主要完成对目标的海上测控任务；测量船在新建之时或大修之后均要对搭载的测控系统进行标校，主要是进行海上合作目标校飞；海上校飞过程中锚泊状态下天线对塔相位标校必不可少，对此进行研究有助于提高锚泊状态下对塔相位标校过程的认识，提升船载测控系统的标校精度；研究过程首先分析了我国测量船所采用的差模双通道单脉冲雷达的跟踪原理和天线对塔校相原理，然后再结合锚泊状态下大型海上测量船的运动规律，建立了船体运动对锚泊状态下对塔校相精度影响的数学模型，最后在远场条件下对数学模型进行了的仿真，分析了测量船锚泊时不同运动模式对相位标校的影响，并进一步给出了锚泊状态下船载测控天线对塔校相的建议。

对塔校相；锚泊；船载测控天线

0 引言

测控雷达系统用来捕获和跟踪空间目标，良好的系统跟踪接收机性能是捕获和跟踪的前提。对于大型船载精密测控雷达系统更是如此，在试验任务之前，科研试验人员都要对其跟踪接收机的方位、俯仰交叉藕合及定向灵敏度进行精确标定，这一工作是保证雷达完成目标捕获及稳定跟踪的必要前提[1-2]，也必不可少。为了保证在海上测控任务中船载测控雷达系统能具有良好的跟踪性能，跟踪接收机系统方位、俯仰必须具有良好的拉偏线性度，即方位、俯仰的交叉藕合度要小，也就是天线在方位上运动时俯仰方向的跟随运动要小，在俯仰上运动时方位方向的跟随运动要小，且方位、俯仰定向灵敏度满足系统要求，也即天线相对于目标运动所产生的偏置电压不大也不小，太大过于敏感，太小过于迟钝，这一工作是通过对跟踪接收机进行标校完成的[3-4]，即相关文献中常说的校相。

目前，常用的校相方法主要有标校塔法、卫星法和射电星法3种[3-5]。标校塔法具体是找一个一定高度的固定目标，在其是架设标校设备，主要是喇叭、信号源等，然后将待标定的系统天线对准标校喇叭，进行技术指标标定，对于测量船来说在码头专门有标校塔，在近海进行校飞则需要人员上岸临时选定建筑物架设标校设备。标校塔法是一种传统的校相方法，具有简单、实时性好，校相结果稳定度高等优点[6-7]，而卫星法和射电星法都依赖地球外的目标，时间上有限制。因此，尽管存在卫星法和射电星法等其它方法，测量船在近海校飞期间仍选择上岸架标的方式进行接收机标校[7]。

航天测量船是我国完成空间目标的主要海基平台，在我国航天器测控任务中发挥着不可替代的作用。对于航天测量船来说，不管是新的航天测量船建造或旧的航天测量船大修，都要进行设备的精度标校，这一工作具体是通过合作目标近海校飞的方式对船载测控系统进行精度标校完成的[8]，由于标校塔法的优点，在锚泊状态下接收机对塔相位标校工作就成为其中重要的一项，具体实施时，人员选定岸上建筑物，将喇叭、信号源等标校设备运至建筑物，船舶则锚泊在海上，天线对准标校喇叭进行相位标定工作。锚泊状态下船体是运动的，这不同于岸基的天线，也不同于船舶在码头的状态，船舶的运动会对校相精度产生影响，影响的大小如何，如何减低影响是本文的研究重点。本文在分析差模双通道单脉冲雷达的跟踪原理、校相原理基础上，结合锚泊状态下船体运动规律对此展开研究，分析船体运动对校相精度的影响，并进一步给出锚泊状态下对塔校相的建议。

1 校相理论基础[9-10]

1.1 双通道单脉冲角误差信号的形成机理

我国的航天测量船上有不同频段的测控系统，其天线都是采用的单脉冲双通道角跟踪体制。这一体制的工作机理如图1所示，主跟踪接收模块分为和通道、差通道两通道，和通道主要是完成载波信号的接收与捕获，给出目标信号大小与锁定状态，输送给天线的伺服系统，天线伺服系统对其进行判断，完成对目标的确认。但对目标跟踪的完成是通过差通道给出的信号来完成的。

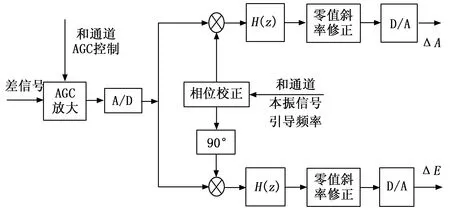
图1 双通道单脉冲体制角误差解调示意图

差通道包含了目标相对天线指向在方位和俯仰方向上的偏离程度，即角误差信号。通过相关幅度检波完成角误差信号解调，并进一步输出给天线伺服系统，天线伺服系统通过角误差信号完成对目标运动方向的识别，进而完成跟踪。天线跟踪目标过程中角误差信号形成的原理如图2所示，设测控天线的辐射中心为O点,空间目标位置为P点，空间目标的视轴方向OP,测控天线电轴方向OO′，OO′与OP的空间夹角为θ，该角度为目标偏离天线电轴方向的任一空间角，可以分解为天线的方位方向和俯仰方向的角度。又定义φ是天线电轴与目标P点构成的平面与水平面的夹角，只考虑来波及地面天线均为理想的圆极化的情况。设P点目标的信标信号为Us=Ue-jwt,与目标偏离的空间角度θ和水平夹角φ无关。首先，P点的信标信号在馈源(正交模耦合器)激励起基模TE11，也即和信号，该信号在馈源和端口输出为数学表达为：

u∑(t)=Ucosωt

(1)

式中,ω为信标信号角频率。

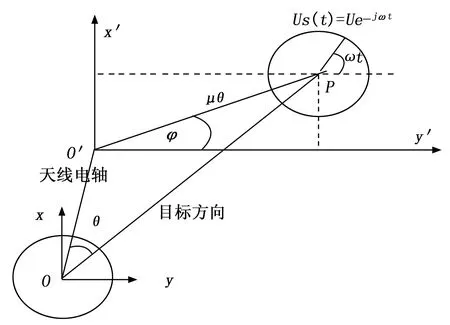
图2 双通道单脉冲角误差信号示意图

由于目标偏离天线轴向，信标信号同时在馈源的跟踪模耦合器中激励起高次模TE21，此为差信号，其通过差信道输出，具体的数学表达的误差电压为：

uΔ(t)=μθUsin(ωt+φ)=

μθUcosφsinωt+μθUsinφcosωt

(2)

式中,μ为差方向图归一化斜率；U为信号强度。

式中，φ为误差信号的取向角，也即信号与方位(水平)方向的夹角，当φ=0°时，只有方位角误差分量，信号为uΔAZ(t)，也即式(3)；当φ=90°时,只有俯仰角误差，信号为uΔEL(t)，也即式(4)。

uΔAZ(t)=μθUcosφsinωt

(3)

uΔEL(t)=μθUsinφcosωt

(4)

1.2 双通道单脉冲角误差信号的解调原理

双通道单脉冲角误差信号的处理过程如图1所示，测控天线主跟踪接收模块接收到和路信号，将其AGC控制信号送给差路，完成差路信号的AGC控制。再进行归一化处理，可以得到和u∑(t)、差uΔ(t)信号分别为：

u∑(t)=cos(ω′t+φ1)

(5)

(6)

式中：ω′为跟踪接收机角鉴相器前信号的中频角频率；φ1、φ2为分别为测控天线的和、差两信道引入的相移；KD、KS为分别为测控天线的和、差信道的传输系数。

测控天线接收的和u∑(t)、差uΔ(t)信号通过角鉴相器鉴相、低通滤波器滤波处理之后得到:

(7)

如果测控系统经过标校，接收处理较好,没有交叉耦合出现，且天线的和信道、差信道的相移差φ2-φ1=0°或φ2-φ1=180°，那么系统只产生方位方向的角误差，俯仰方向的角误差分量为0。

上述是方位方向角误差信号的解调，俯仰方向的误差信号的解调与此相类似，只是处理时要将和信号经90°移相后，再与差信号一同经角鉴相器鉴相，低通滤波器滤波处理后得到：

(8)

当天线的和信道、差信道的相移差φ2-φ1=0°或φ2-φ1=180°时，得到俯仰误差电压为：

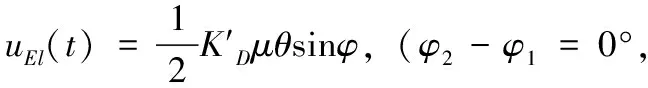
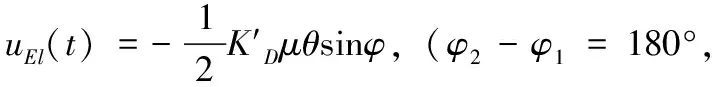
1.3 测控天线校相的基本原理

从上述过程看出，当天线的和信道、差信道的相移差不为0度或180度时，目标在天线方位方向上运动不仅会引起方位误差，还会引起俯仰误差，也即交叉藕合。为了确保输出的角误差不存在交叉藕合项，就必须对和差通道引入的相移进行处理，使得最终呈现的相移φ2-φ1等于0°或180°，这一工作即是测控系统的跟踪接收机通过校相来完成的。目前，实际应用过程中对塔校相时只对方位俯仰中的一路进行校相，计算出相移处理角度，另一路则加上90度即可，一般进行方位的校相，其具体步骤如下：

(1)找目标零点，即使天线对准标校目标，此时天线敏感的目标方位、俯仰角误差均为零，此为零点；

(2)控制天线旋转，使目标在天线方位上偏开一定角度θE，一般为3 mil，俯仰方向上不变。此时水平夹角φ=0°，公式(7)变为：

(9)

调整和支路移相器，从0度开始以一定角度为间隔(一般为0.35度)步进加入附加相位Δφ，寻找使接收到的方位角误差信号uAz(t)为0的相移处理角度，即φ2-(φ1+Δφ)=90°，则以和支路为参考的和差支路相位差φ2-φ1=90°+Δφ，此即为需代入的相位修正值。

2 锚泊状态下校相过程

依据文献[11]的仿真研究，长度200米以上的船在锚泊状态下的运动轨迹近似圆周，圆周中心为锚点，此处简化为船在水平面内进行平移与旋转运动。如图3所示，假设天线初始中心为O0，目标为P，目标的垂直高度为H，与天线中心的水平距离为L。以O0点为中心建立坐标系O0X0Y0Z0，O0X0Y0为水平面，P在O0Y0Z0平面内，并在O0X0Y0内的投影为O1，O1X1平行于O0X0。校相时，天线偏开θE然后软件开始计算相位，这需要一定时间，假设此时间内天线中心随船平移至O点，坐标为(x0,y0,0)。此时，天线空间实际指向由O0P变为OP′，尽管这两个指向在空间中是平行的，但目标P在天线的视场内的位置已发生改变。由于校相时天线始终处于大地工作方式，可以认为船的旋转不影响天线在空间中的指向。

图3 锚泊时角误差信号的形成示意图

依据测控天线对塔的校相过程，测控天线指向偏开目标一定角度θE，此时天线实际指向再次发生改变，变为OP″。由1.2节介绍，天线获得的方位误差电压为：

(10)

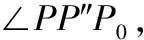
由于校相过程中首先求得使uAz(t)=0的Δφ，此处记为Δφ1，即：

(11)

由式(11)可以看出计算Δφ1与θ没有关系，θ只影响了定向灵敏度。

进一步有：

cosφcos(φ2-φ1-Δφ1)=sinφsin(φ2-φ1-Δφ1)

(12)

可得：

(13)

若没有船舶移动，计算的结果为Δφ0=φ2-φ1-90°。

两者差值为：

(14)

(15)

3 仿真分析

文献[8]给出了船载USB统一测控天线的远场条件，如表1所示。

表1 船载USB统一测控系统远场条件统计表

考虑到海上测量船锚泊、架标均有一定自由度，此处即选定表1中的参数作仿真条件，即高度为115米，距离为2208米，测控系统相位标定时，一般测控天线方位方向上正偏3个密位，即θE≈0.003 rad，此条件下对船舶X方向、Y方向进行运动仿真，分析的结果如下：

(1)测量船X方向的位移与相位误差关系如图4所示，从图中可以看出在天线方位方向正偏3个密位的情况下，随着测量船X方向位移大于-6米时，标定的相位误差急剧变，并随着测量船Y方向位移增大而变大，这意味着水流导致测量船向负X方向运动时，标定的相位误差有很大的不确定性。从图4还可以看出。在测量船X正方向位移处误差几乎没有，所以此处建议在锚泊状态下对塔校相时首先观察水流导致的测量船在X轴上的运动方向，具体做法是大地方式下天线对准信标，观察目标方位误差电压变化情况，如果变正，则意味着船舶向X轴负向运动，此时校相时应进行方位负偏，反之进行正偏。

图4 测量船X方向的位移与相位误差关系图

(2)测量船Y方向的位移与相位误差关系如图5所示，从图中可以看出标定的相位校正误差随着测量船Y方向位移增大而增大，且测量船X方向上的位移越大，这种影响越小。此意味着锚泊地选择时或对塔相位标定时应考虑水流的方向，尽量使水流方向与天线和信标连线方向垂直，这样可以减少标定的相位误差。

图5 测量船Y方向的位移与相位误差关系图

(3)信标高度与标定的相位误差关系如图6所示，从图中可以看出信标高度越低，误差越小，但考虑到仰角太低，多径效应引起的误差明显。因此，架标时在满足多径效应误差要求的情况，信标越低越好。

图6 信标高度与相位误差关系图

(4)不同信标高度下测量船和信标的水平距离与相位误差关系如图7所示(X=1米，Y=1米)，从图中可以看出，同一距离下信标越低，误差越小，同上一段结论，并且随着距离大于2公里后，误差变化已不明显。但距离太远后，同一高度的信标相对低仰角要低，因此，此处建议锚泊距离在2公里即可。

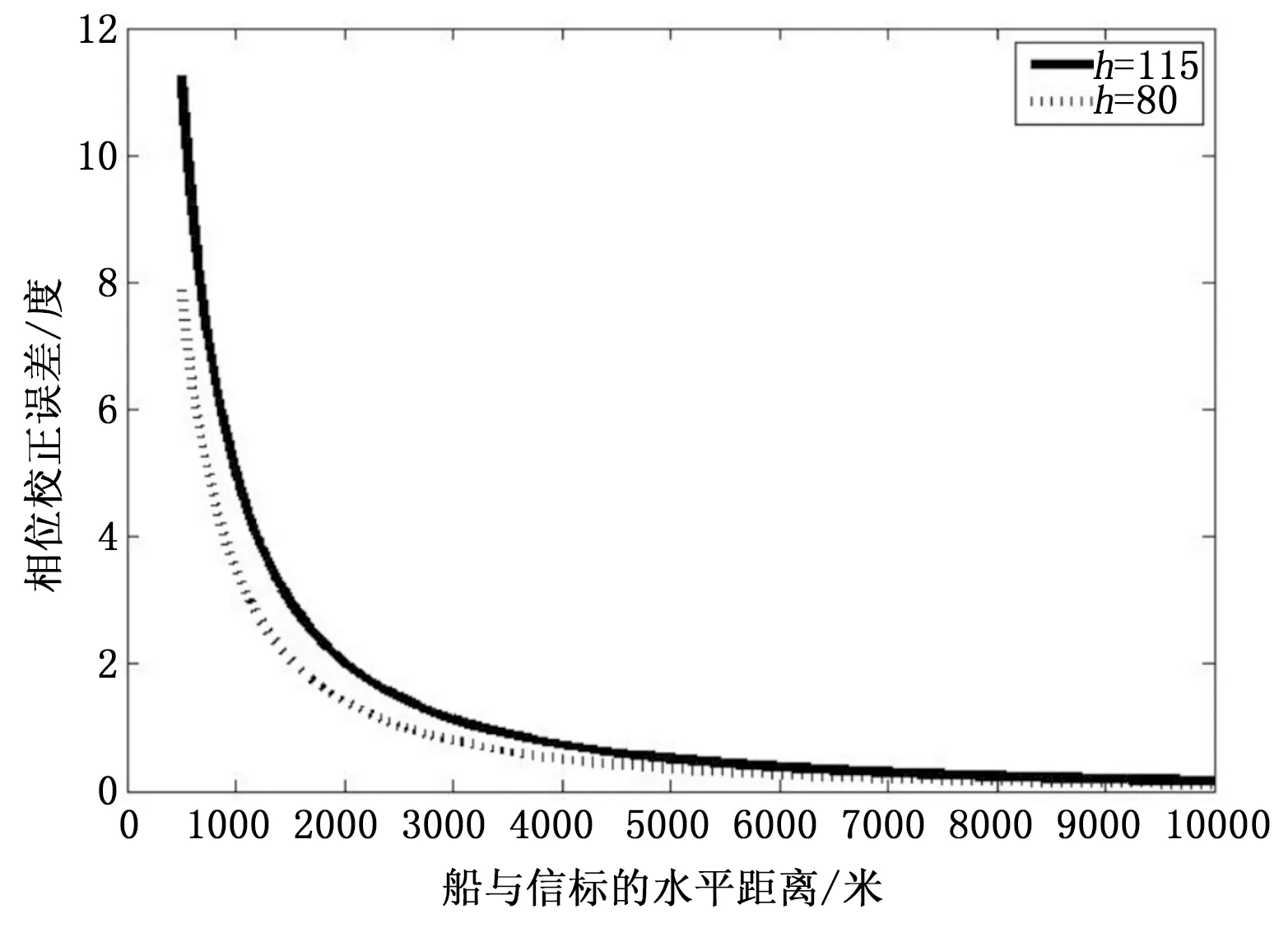
图7 船和信标的水平距离与相位误差关系图

4 结论

海上测量船是我国航天测控网中不可或缺的重要一环，也是目前唯一的海基测控平台，对高精度的海上测控系统进行研究非常必要。本文针对海上测量船在新建和大修中必需进行的海上校飞工作为研究对象，重点分析研究了锚泊状态下船载测控天线对塔校相的过程。论文首先分析了差模双通道单脉冲雷达的跟踪原理以及具体的校相过程，并在此基础上，结合锚泊状态下海上测量船的运动规律，对校相误差进行了定量分析，建立了相位误差模型，并对模型进行仿真分析，仿真结果表明船舶在与船信标平面相垂直的方向上的运动对校相误差影响较大，尤其是当船舶运动方向与校相过程中天线的偏置方向相同时误差极大。为减少此影响，本文建议天线方位偏置方向应与船舶运动方向一致。另外信标设备的高度对校相也有一定影响，本文建议上岸架标时在满足多径效应影响的前提下尽量将信标架低。

[1] 房新兵,毛南平,刘向前,等.船载测控雷达无塔角度标校新方法[J]. 电讯技术, 2010, 50(12):116-120.

[2] 毛南平,丛 波.近场效应对一种C频段统一测控雷达角度标校数据的影响分析[J].电讯技术,2004,48(4):65-68.

[3] 魏明山,葛铁志,杜潇淞,等.大口径天线多模馈源跟踪系统校相参数的计算[J].电讯技术,2015,55(7):741-745.

[4] 胡乐宏.波束波导天线馈源与校相技术研究[D].南京：南京理工大学，2012.

[5] 瞿元新, 毛南平.船载X频段微波统一测控系统快速校相方法[J].遥测遥控, 2014, 45(3): 69 -72.

[6] 苏 勋,席文君，等.双通道跟踪接收机对地校相技术[J].电讯技术,2012,52(3):268-272.

[7] 张振庄,耿大孝.船载天线动态校相技术研究与实现[J].无线电通信技术, 2015, 41(1): 52-55.

[8] 瞿元新. 船载微波统一测控系统概论[M].北京:国防工业出版社出版,2015.

[9] 刘童岭,邵长宝,周成刚.船载雷达无塔动态相位标校方法研究[J]. 科学技术与工程,2011,24(8):5989-5993.

[10] 仇三山.双通道单脉冲跟踪快速校相改进算法[J].四川兵工学报, 2013, 34(5): 96-98.

[11] 宋 扬.基于AIS数据的大型船舶锚泊半径及船间距的研究[D].大连:大连海事大学，2010.

StudyonTowerPhaseCalibrationforShip-borneTTamp;CSystematAnchor

Yang Wenjing, Wu Hao, Yang Guo

(China Satellite Maritime Tracking and Control Department, Jiangyin 214431, China)

An instrumentation ship of spacecraft is an offshore platform with ship-borne TTamp;C system. Its role is to marine measurement and control mission. When the instrumentation ship is built or overhauled, the ship-borne TTamp;C system shall be calibrated. The tower phase calibration for ship-borne TTamp;C system at anchor is essential. This study will help to improve the understanding of the calibration process of tower phase calibration under mooring conditions and improve the calibration accuracy of ship-borne TTamp;C system. Based on the differential mode tracking principle and phase calibrating principle of dual-channel monopulse radar, the relationship between phase calibration error and ship movement was analysed and simulated under the condition of far field. According to the simulation conclusion, some proposals about phase calibration of ship-borne TTamp;C system at anchor are offered in this paper.

tower phase calibration; at anchor; ship-borne TTamp;C system

2017-02-26；

2017-03-24。

杨稳竞(1985-)，男，江苏滨海人，硕士，工程师，主要从事航天器海上测控方向的研究。

1671-4598(2017)09-0001-04

10.16526/j.cnki.11-4762/tp.2017.09.001

TN95

A