基于混合搜索的多种群人工蜂群算法

陈 皓,张 洁,杨清萍,董娅娅,肖利雪,冀敏杰

(西安邮电大学 计算机学院,西安 710121) (*通信作者电子邮箱chenhao@xupt.edu.cn)

基于混合搜索的多种群人工蜂群算法

陈 皓*,张 洁,杨清萍,董娅娅,肖利雪,冀敏杰

(西安邮电大学 计算机学院,西安 710121) (*通信作者电子邮箱chenhao@xupt.edu.cn)

针对经典人工蜂群(ABC)算法搜索策略存在搜索机制单一、群体全局搜索与局部搜索运算耦合性较高的问题，提出一种基于混合搜索的多种群人工蜂群(MPABC) 算法。首先，将种群按照适应度值进行排序，得到一个有序队列，进而将其划分为随机子群、核心子群和平衡子群三类有序子群；其次，针对不同子群结合相应的个体选择机制与搜索策略，构建出不同的差异向量；最后，在群体的搜索过程中，通过三类子群实现对具有不同适应度函数值个体的有效控制，来增强群体全局搜索和局部搜索的平衡能力。通过对16个标准测试函数进行仿真实验并与具有可变搜索策略的人工蜂群(ABCVSS)算法、基于选择概率的改进人工蜂群(MABC)算法、基于粒子群策略的多精英人工蜂群(PS-MEABC)算法、基于符号函数的多搜索策略人工蜂群(MSSABC)算法和优化高维复杂函数的改进人工蜂群(IABC)算法共五种典型的蜂群算法进行了对比，实验结果显示MPABC具有较好的优化效果；与ABC算法相比，MPABC在求解高维(100维)复杂问题上的收敛速度提高了约23%，且求解精度更优。

人工蜂群算法；个体选择机制；差分搜索；群体分类控制策略

0 引言

人工蜂群(Artificial Bee Colony, ABC)算法[1]具有结构简单、控制参数少、性能优良等特点,目前已被应用于解决多种不同的实际优化问题[2-5],并取得了较好的实验结果。但在ABC中,雇佣蜂和观察蜂所采取的搜索策略在求解复杂函数时存在着过早收敛、容易陷入局部最优、求解精度不高等缺点。为此,研究者提出了许多不同的搜索策略来改善算法性能,其中的代表性研究工作是关于如何改进解搜索方程或提出新的解搜索方程[6]。Zhu等[7]受粒子群优化(Particle Swarm Optimization, PSO)算法启发,提出在解搜索方程中加入全局最优解gbest信息引导ABC算法。另一研究趋势是探索如何与其他搜索算子相结合来提高算法搜索性能。比如,Gao等[8]通过将ABC与局部搜索Powell方法相结合,有效地提高了ABC的性能。

上述通过直接修改进化操作算子的方法虽一定程度上提高了算法性能,但其都是在具体操作层面上的改进,并没有充分考虑种群全局结构和局部算子的个体能力问题[9],没有从根本上解决在提高算法收敛性的同时该如何增加种群的多样性、避免陷入局部最优的问题,其根本原因在于搜索策略的调节仍是被动适应[10]。因而,为有效解决蜂群间通信方式单一、协作不足所引发的种群在全局探索与局部寻优不平衡的问题，本文通过研究个体选择方式与搜索运算的性能特点间的联系,提出了一种基于混合搜索的多种群人工蜂群(Multi-Population ABC, MPABC)算法,该算法利用个体选择机制提升其在进化过程中的自我调节能力,并通过融合多种进化策略改进种群的搜索效率与抗早熟能力。

1 ABC算法的基本计算机制

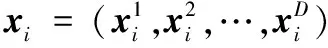
(1)

2)观察蜂阶段。雇佣蜂完成勘探后,观察蜂根据雇佣蜂分享的信息,以轮盘赌方式选择一个食物源进一步开采,则食物源被选中的概率为:

(2)

其中:fiti为第i个食物源的适应度函数值。对于最小化问题,fiti与问题空间S的目标函数值trueFiti对应关系为:

(3)

3)侦察蜂阶段。当雇佣蜂对应食物源的适应值连续limit次未更新,表明该食物源已被开采尽,则对应雇佣蜂就放弃该食物源并变成侦察蜂,同时随机产生一新食物源:

(4)

为进一步研究ABC算法的计算机制,图1～2给出了单峰函数F06(Step)与多峰函数F09(Rastrigin)利用ABC在搜索最优解过程中函数收敛曲线与群体多样性曲线。参数设置为:迭代次数Max.FE=1 000次；控制参数limit=10,80次;收敛精度为10-5。其中，收敛精度取对数后，所得函数值为-5，则收敛精度曲线与横坐标相互重合。

为了便于对ABC性能的分析,首先给出一些基本定义:

定义1 个体xi和xj之间的相似性可通过欧氏距离比Disij来度量:

Disij=Dis(xi,xj)=‖xi-xj‖/‖xub-xlb‖

(5)

其中:‖xi-xj‖表示两个实数向量的欧几里得范数。显然Disij在区间[0,1]内,Disij愈趋近0,个体差异性越小;反之则相反。

定义2 群体的平均间距meanDis为:

(6)

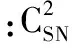
图1 函数收敛曲线

图2 函数多样性曲线

limit作为ABC算法中衡量全局搜索代价的重要参数,直接关系到算法的计算性能与收敛速度。如图1～2所示,当函数F06与F09的limit值较小时,算法虽然具有较强的随机性能与全局搜索性能,但其收敛速度非常缓慢且精度远没有达到实验要求；当limit较大时,算法虽然增强了局部搜索能力,提升了收敛速度,但却因受到局部最优解的束缚而陷入早熟收敛。以上分析说明limit的取值差异使式(1)参数倾向于不同搜索策略,偏向全局搜索的参数使曲线表现出过度的全局搜索趋势,偏向局部搜索的参数使曲线表现出过度的局部搜索趋势,其根本原因在于ABC单一搜索模式具有的较高的耦合性,难以实现全局搜索和局部搜索间的有效协调。

2 基于子群与多进化策略的改进机制

2.1 子群的构造机制

针对上述研究中的不足,通过对个体间编码差异及其问题空间的分布与其所参与搜索运算的性能特点间存在的联系[11]进行研究,发现其主要表现为个体编码差异对搜索运算的控制,或是个体空间分布形态所形成的结构对系统整体计算的调节,但这种隐式的结构关系并不利于其对计算过程的主动控制。因此,就需要设计出一种更为明显的种群关系。

队列作为实际生活中一种常见的有序群体,其特点是队头与队尾个体差异较大,中间个体差异较小且数目众多,这说明有序队列不同位置中的个体之间具有一定间距关系。基于以上分析,本文提出一种新思路,将种群先按适应值大小进行排序,分为三类有序子群;再通过子群控制个体的选择范围,以构建出不同的差异向量进行群体搜索。

(7)

其中:Rg、Cg和Bg分别表示随机子群、核心子群和平衡子群;Nrand表示随机子群的个体总数;Nother=SN-Nrand表示Cg和Bg的个体总数;μ是群体划分比例,实验取值为0.3。

图3是由式(7)得到的种群类结构图,子群内个体相似性最大,而子群间差异性最大。因而,本文利用这三类子群实现对具有不同适应度函数值个体的有效控制,以达到调节全局和局部搜索的目的。

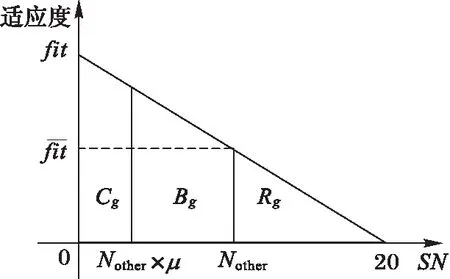
图3 基于适应值排序的种群类结构

2.2 分类机制对群体搜索状态的影响分析

2.2.1 利用分类结构调节全局和局部搜索过程

本节从两方面分析算法是如何利用三类子群实现对群体搜索过程的调节：一是通过对三类子群的平均间距进行分析,说明其可调节全局与局部搜索的原因；二是利用个体选择机制实现其对搜索过程的调节。图4和图5分别表示函数F03(SumPower)运用MPABC算法在搜索最优解过程中子群的平均间距meanDis与个体数目number的变化曲线,实验结果为20次独立实验(参数为D=30,Max.FE=1 000)的平均值。

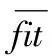
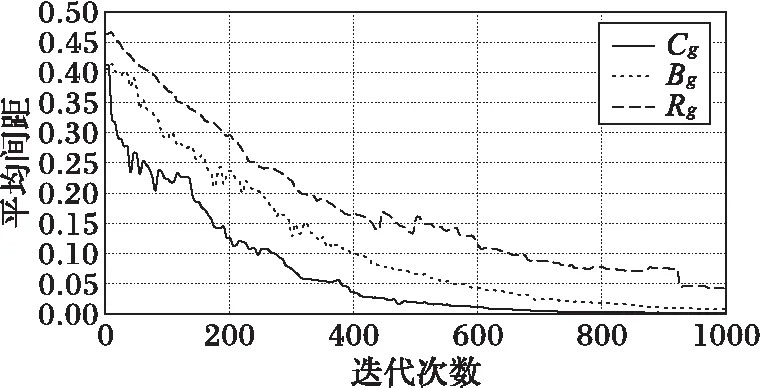
图4 三类子群平均间距在进化过程中的变化曲线

另外,根据三类子群间独立又彼此联系的结构,可以方便地将具有不同计算结构和运算特性的搜索方法有效结合在一起,通过个体选择机制实现对群体全局和局部搜索的动态调节。如图5所示,进化过程分为三个阶段,其中,Cg与Bg的个体数目不断增大,Rg数目却逐渐减小,这种变化使看起来独立的各类子群之间又彼此关联。

图5 进化过程Cg、Bg和Rg的个体数目变化曲线

基于以上分析,针对不同的搜索水平设计出一种新型的个体选择机制:

Cg的局部搜索:

{ci|ci∈Cg,i=p1,p2}

(8)

Bg的全局到局部的过渡搜索:

{bi|bi∈Bg,i=p1,p2}

(9)

Rg的全局搜索:

{ri|ri∈Cg∪Bg∪Rg,i=p1,p2,…,p5}

(10)

其中:ci表示在Cg中随机选出2个个体,记为cp1和cp2;同理bi与ri分别表示在Bg与Rg中选出的个体。

进化搜索中三类子群的搜索频率由个体数目决定,故其取值大小将直接影响每代进行全局及局部搜索的比例。进化前期,Rg在群体中number值比重最大且Bg与Cg比重较小,形成以“全局搜索方式为主与其他搜索方式为辅”的计算机制,有效地丰富了群体多样性并降低了算法早熟收敛的可能;进化中期,三类子群number值均处于一种相对稳定的状态,形成了一种“过渡搜索+全局搜索+局部搜索”的搜索组合;而随着Cg中number逐渐增大,其他子群值的不断减小,使得进化后期形成了以“局部搜索和过渡搜索为主与全局搜索方式为辅”的计算机制,从而提高了算法寻找最优解的速度。

2.2.2 基于分类调节的新型差分进化算法计算机制的性能分析

为有效降低ABC算法搜索机制因单一盲目性所带来的负面影响,在分类调节机制的基础上通过进一步引入差分进化(Differential Evolution, DE)算法的多种搜索方式,有效地提高了系统的计算效率。为了便于研究,将DE的五种进化模式分为三类[12],其特点是:第一类模式中个体自由探索性突出,全局收敛较强,不易陷入局部最优,但收敛速度较慢；第二类模式的个体在该区域的自由探索性相对较弱,局部收敛性和继承性较强,收敛速度较快,但易陷入局部最优；第三类模式特点是群体自由探索性和继承性相对保持均衡,具有良好的适应性。

通过以上分析,为有效提升算法的搜索性能，本文按照子群平均间距值对种群的搜索水平进行类别划分,则三类子群的搜索机制如下:

Cg搜索策略:

(11)

Bg搜索策略:

(12)

Rg搜索策略:

(13)

根据每个个体在搜索过程中的不同表现,对于不同子群的个体,在寻优过程中它需要加强该子群所需要的能力。即,在Cg中加强局部寻优来搜索极值点,Rg中通过全局搜索来增强算法的勘探能力,而Bg主要是对算法全局搜索能力和局部搜索能力的协调。

2.3 基于多进化模式协作的人工蜂群算法

在前述基础上提出了一种新算法MPABC,即在分类调节机制的基础上进一步引入DE计算机制来改进全局与局部的计算效果。图6为MPABC的架构。

图6 MPABC的架构

如图6所示, MPABC计算模式分为三大模块:模块一是系统初始化,包括种群初始化与子群的构建,最后得到三类有序子群体;模块二针对不同子群设计出一种更具针对性且协调性更佳的搜索机制组合,实现对搜索过程的调节;模块三是利用观察蜂进行局部寻优来找出最优解。先通过式(8)～(9)计算出观察蜂的搜索区间,再利用式(11)进行局部搜索,进一步提升算法的寻优能力。

3 仿真实验及结果分析

为验证MPABC的求解性能,采用16个典型的Benchmark[13]146函数(F01～F16)用于仿真实验。其中：F01～F08是单峰函数；F06是非连续函数；F07是带噪声函数,在维度大于3时为多峰函数;F09～F16是多峰函数。通常单峰函数用于测试算法的寻优精度以及考察算法的执行性能。而多峰函数中的局部最优点会伴随维数的增加而指数增长,常用于检验算法跳出局部最优的能力。

整个实验分为两部分：第一部分是对ABC和MPABC的优化性能与测试结果进行比较；第二部分是将其与近年的ABC变种算法进行比较分析,包括具有可变搜索策略的人工蜂群算法(ABC algorithm with Variable Search Strategy, ABCVSS)[13]148-151、基于选择概率的改进人工蜂群算法(Modified ABC algorithm based on selection probability, MABC)[13]152、基于粒子群策略的多精英人工蜂群(Particle Swarm-inspired Multi-Elitist ABC, PS-MEABC)算法[14]、基于符号函数的多搜索策略人工蜂群(Multi-Search Strategy of the ABC, MSSABC)算法[15]和优化高维复杂函数的改进人工蜂群算法(Improved ABC algorithm for optimizing high-dimensional complex functions, IABC)[16]。

3.1 MPABC和ABC的收敛性比较

为验证MPABC的寻优能力在复杂高维函数的有效性。将MPABC与ABC从结果精度、收敛速度和维度扩展性三个方面进行比较分析。实验参数设置为:NP=40;limit=200;D=30,60,100;Max.FE=5 000;收敛精度为10-5。表1给出了当D=30,60,100时算法的测试结果(每个函数独立运行20次)。其中：最优值和最差值反映了解的质量,平均值反映了在给定最大评价次数时算法的求解精度,标准差则反映了算法的稳定性和鲁棒性。

由表1计算结果可以看出：在30维情况下,MPABC在大部分函数上的性能要显著优于ABC。对部分函数(如F05、F07、F08、F12和F14),两者性能相当;尤其是在函数F06、F09～F11上,ABC与MPABC均能取得理论最优值0。而对于其他函数(F01～F04),MPABC的收敛精度比ABC则有了大幅度提升。并且随着维度的增长,MPABC的求解结果仍要优于或同ABC一样得到理论最优值0(如函数F06、F11)。

函数无论是在30、60还是100维上,MPABC算法的最优值和最差值的精度与ABC相比得到明显提高,并且对各测试函数均具有较高的寻优精度,尤其在函数F01～F04、F10、F11上。其次,在相同迭代次数下,针对绝大部分函数(F01、F03、F6～F11、F13～F14),MPABC算法寻优速度更快。其中一部分原因是系统利用种群分类结构直接控制群体的搜索过程,实现对全局和局部搜索过程的调节;另一部分是因为在分类调节机制的基础上进一步引入DE计算机制来改进全局与局部的计算效果,使MPABC在计算的不同阶段形成更具针对性且协调性更佳的搜索机制组合,实现了在不同复杂结构的问题空间中更高效、稳定的搜索。

表1 ABC与MPABC算法的测试结果

为了直观反映MPABC的收敛性能,图7～8给出了两种算法对于部分测试函数在D=30,Max.FE=200时的收敛曲线与群体多样性图。从图7～8可以看出,MPABC虽然在迭代初期的性能略差,但随着迭代次数的增加,函数收敛曲线和群体多样性曲线的下降速度明显高于ABC算法,有利于群体在后期快速收敛到较高精度的解。

由图7的收敛曲线可以看出:MPABC算法不但在函数F06上找到理论最优值0,而且其收敛速度明显高于ABC;在复杂非线性函数F08和多模态函数F15上,MPABC的性能仅略优于ABC;而对多模态函数F13和F14,MPABC的收敛精度和速度均显著高于ABC。由图8的多样性曲线可以看出,MPABC的群体多样性值在前期仅略高于ABC,能够较好地减缓算法在前期的收敛速度;随后MPABC算法的群体多样性迅速降低并逐渐趋于0,其多样性明显低于ABC算法。此时群体差异性最小,促使其加速收敛到最优值。综上,说明改进后的MPABC算法性能优于ABC。

图7 函数的收敛曲线

图8 函数的多样性曲线

3.2 MPABC和其他改进算法的比较

将MPABC与近几年所提出的改进算法ABCVSS、MABC、PS-MEABC、MSSABC、IABC在D=30时进行比较。为了比较的公平性,MPABC参数设置为Max.FE=5 000,limit=200;另外5种算法参数均为Max.FE=5 000×D,limit=SN×D,其余参数保持不变,实验数据直接取自各文献。

由表2可以看出,在16个基准测试函数中,6种算法在函数F06、F09～F11上都能求得理论最优值;对于其他函数,MPABC在解的精度和稳定性上明显优于ABCVSS、MABC、PS-MEABC、MSSABC,在绝大部分函数上则优于IABC。

从上述实验结果可以看出,MPABC算法可以在较小的评价次数下达到相同甚至更高的精度。不仅具有较强的全局搜索能力,而且具有较强的局部搜索能力,能有效克服ABC算法收敛速度慢和易陷入局部最优的缺陷,并随着函数维度的增加,仍能保持较好的有效性和鲁棒性。

4 结语

本文提出在种群分类调节机制的基础上进一步引入DE计算机制来改进种群全局与局部的计算效果,形成了一种新型的进化搜索算法,基于混合搜索的多种群人工蜂群算法。对16个基准测试函数的仿真实验结果表明,算法有效克服了ABC演化过程中局部停滞的问题,能有效处理高维函数优化问题并获得较高的寻优精度。但其也存在局限性,例如对Schwefel 2.26(F12)函数的求解效果并不理想。因而,如何使算法能够在函数上表现出更好的性能以及将本文算法应用到多目标优化、约束优化等领域将是下一步的研究工作。

表2 ABCVSS、MABC、PS-MEABC、MSSABC、IABC和MPABC算法结果对比

References)

[1] KARABOGA D. An idea based on honey bee swarm for numerical optimization: TR06[R]. Kayseri: Erciyes University, Engineering Faculty, 2005: 10.

[2] 冀俊忠, 魏红凯, 刘椿年, 等. 基于引导素更新和扩散机制的人工蜂群算法[J]. 计算机研究与发展, 2013, 50(9): 2005-2014. (JI J Z, WEI H K, LIU C N, et al. Artificial colony algorithm based on introductory updating and diffusion mechanism[J]. Journal of Computer Research and Development, 2013, 50(9): 2005-2014.)

[3] EBRAHIMNEJAD A, TAVANA M, ALREZAAMIRI H. A novel artificial bee colony algorithm for shortest path problems with fuzzy arc weights[J]. Measurement, 2016, 93: 48-56.

[4] YIN P Y, CHUANG Y L. Adaptive memory artificial bee colony algorithm for green vehicle routing with cross-docking[J]. Applied Mathematical Modelling, 2016, 40(21/22): 9302-9315.

[5] NSEEF S K, ABDULLAH S, TURKY A, et al. An adaptive multi-population artificial bee colony algorithm for dynamic optimization problems[J]. Knowledge-Based Systems, 2016, 104: 14-23.

[6] 周新宇, 吴志健, 王明文. 基于正交实验设计的人工蜂群算法[J]. 软件学报, 2015, 26(9): 2167-2190. (ZHOU X Y, WU Z J, WANG M W. Artificial colony algorithm based on orthogonal experiment design [J]. Journal of Software, 2015, 26(9): 2167-2190.)

[7] ZHU G, KWONG S. Gbest-guided artificial bee colony algorithm for numerical function optimization[J]. Applied Mathematics amp; Computation, 2010, 217(7): 3166-3173.

[8] GAO W F, LIU S Y, HUANG L L. A novel artificial bee colony algorithm with Powell’s method[J]. Applied Soft Computing, 2013, 13(9): 3763-3775.

[9] 李文锋, 梁晓磊, 张煜. 具有异构分簇的粒子群优化算法研究[J]. 电子学报, 2012, 40(11): 2194-2199. (LI W F, LIANG X L, ZHANG Y. Research on particle swarm optimization algorithm with heterogeneous clustering [J]. Acta Electronica Sinica, 2012, 40(11): 2194-2199.)[10] 周传华, 谢安世. 一种基于动态小生境的自组织学习算法[J]. 软件学报, 2011, 22(8): 1738-1748. (ZHOU C H, XIE A S. A self-organizing learning algorithm based on dynamic niche [J]. Journal of Software, 2011, 22(8): 1738-1748.)

[11] 陈皓, 潘晓英. 类搜索算法[J]. 软件学报, 2015, 26(7): 1557-1573. (CHEN H, PAN X Y. Clustering search algorithm[J]. Journal of Software, 2015, 26(7): 1557-1573.)

[12] 贺毅朝, 王熙照, 刘坤起, 等.差分演化的收敛性分析与算法改进[J]. 软件学报, 2010, 21(5): 875-885. (HE Y Z, WANG X Z, LIU K Q, et al. Convergence analysis and algorithm improvement of differential evolution[J]. Journal of Software, 2010, 21(5): 875-885.)

[13] KIRAN M S, HAKLI H, GUNDUZ M, et al. Artificial bee colony algorithm with variable search strategy for continuous optimization[J]. Information Sciences, 2015, 300(1): 140-157.

[14] MA W, SUN Z, LI J, et al. An improved artificial bee colony algorithm based on the strategy of global reconnaissance[J]. Soft Computing, 2015, 20(12): 4825-4857.

[15] 王志刚, 王明刚. 基于符号函数的多搜索策略人工蜂群算法[J]. 控制与决策, 2016, 31(11): 2038-2044. (WANG Z G, WANG M G. Multi-search strategy based on symbolic function artificial bee colony algorithm [J]. Control and Decision, 2016, 31(11) : 2038-2044.)

[16] 王志刚, 王明刚. 优化高维复杂函数的改进人工蜂群算法[J]. 东北师大学报 (自然科学版), 2016, 48(2): 56-64. (WANG Z G, WANG M G. An improved artificial bee colony algorithm for optimizing high dimensional complex functions[J]. Journal of Northeast Normal University (Natural Science Edition), 2016, 48(2): 56-64.)

Multi-populationartificialbeecolonyalgorithmbasedonhybridsearch

CHEN Hao*, ZHANG Jie, YANG Qingping, DONG Yaya, XIAO Lixue, JI Minjie

(SchoolofComputerScienceandTechnology,Xi’anUniversityofPostsamp;Telecommunications,Xi’anShaanxi710121,China)

Aiming at the problems of Artificial Bee Colony (ABC) algorithm, which are the single search mechanism and the high coupling between global search and local search, a Multi-Population ABC (MPABC) algorithm based on hybrid search was proposed. Firstly, the population was sorted according to the fitness value to get an ordered queue, which was divided into three sorted subgroups including random subgroup, core subgroup and balanced subgroup. Secondly, different difference vectors were constructed according to the corresponding individual selection mechanism and search strategy to different subgroups. Finally, in the process of group search, the effective control of individuals with different fitness functions was realized through three subgroups, thus improving the balance ability of global search and local search. The simulation results based on 16 benchmark functions show that compared with ABC algorithm with Variable Search Strategy (ABCVSS), Modified ABC algorithm based on selection probability (MABC), Particle Swarm-inspired Multi-Elitist ABC (PS-MEABC) algorithm, Multi-Search Strategy of the ABC (MSSABC) and Improved ABC algorithm for optimizing high-dimensional complex functions (IABC), MPABC achieves a better optimization effect; and on the solution of high dimensional (100 dimensions) problems, compared with ABC, MPABC has higher convergence speed which is increased by about 23% and better search accuracy.

Artificial Bee Colony (ABC) algorithm; individual selection mechanism; differential search; group classification control strategy

2017- 05- 02;

2017- 07- 19。

国家自然科学基金资助项目(61203311,61105064);西安邮电大学创新基金资助项目(114- 602080126)。

陈皓(1978—),男,河北安新人,副教授,博士,CCF会员,主要研究方向:进化计算、工程优化; 张洁(1992—),女,陕西咸阳人,硕士研究生,主要研究方向:计算智能、数据挖掘; 杨清萍(1992—),女,湖北襄阳人,硕士研究生,主要研究方向:机器学习; 董娅娅(1991—),女,陕西韩城人,硕士研究生,主要研究方向:自然语言处理、数据挖掘; 肖利雪(1992—),女,内蒙赤峰人,硕士研究生,主要研究方向:计算智能、数据挖掘; 冀敏杰(1990—),男,陕西渭南人,硕士研究生,主要研究方向:计算智能、数据挖掘。

1001- 9081(2017)10- 2773- 07

10.11772/j.issn.1001- 9081.2017.10.2773

TP301.6

A

This work is partially supported by the National Natural Science Foundation of China (61203311, 61105064), the Innovation Foundation of Xi’an University of Posts amp; Telecommunications (114-602080126).

CHENHao, born in 1978, Ph. D., associate professor. His research interests include evolutionary computing, engineering optimization.

ZHANGJie, born in 1992, M. S. candidate. Her research interests include computational intelligence, data mining.

YANGQingping, born in 1992, M. S. candidate. Her research interests include machine learning.

DONGYaya, born in 1991, M. S. candidate. Her research interests include natural language processing, data mining.

XIAOLixue, born in 1992, M. S. candidate. Her research interests include computational intelligence, data mining.

JIMinjie, born in 1990, M. S. candidate. His research interests include computational intelligence, data mining.