基于双模糊信息的特征选择算法*

李素姝，王士同，李 滔

江南大学 数字媒体学院，江苏 无锡 214122

基于双模糊信息的特征选择算法*

李素姝+，王士同，李 滔

江南大学 数字媒体学院，江苏 无锡 214122

在对传统特征选择算法进行研究的基础上，提出了一种基于双模糊信息的特征选择算法（feature selection algorithm based on doubly fuzziness information，FSA-DFI）。第一种模糊体现在对最小学习机（least learning machine，LLM）进行模糊化后得到模糊最小学习机（fuzzy least learning machine，FUZZYLLM）中；另一种模糊则是在基于贡献率模糊补充这一方法中体现的，其中贡献率高的特征才可能被选入最终的特征子集。算法FSA-DFI是将FUZZY-LLM和基于贡献率的模糊补充方法结合得到的。实验表明，和其他算法相比，所提特征选择算法FSA-DFI能得到更好的分类准确率、更好的降维效果以及更快的学习速度。

特征选择；双模糊；最小学习机；模糊隶属度；模糊补充

1 引言

大数据的兴起需要更多性能优良的机器学习算法和特征选择新方法。特征选择的目标是为了找到具有代表性的特征子集，能表示出整个数据域的特性。在一个典型的特征选择方法中，包括产生候选子集、评估子集、终止选择以及验证子集是否有效这几步。

对特征选择算法的研究最早可以追溯到20世纪60年代，当时的研究领域主要是在统计学和信号处理方向，涉及到的特征也很少。90年代以来，对大规模数据的预处理问题不断涌现，原有的特征选择算法已不能满足需求，许多学者开始研究新算法。基于互信息的特征选择（mutual information-based feature selection，MIFS）算法[1]是由Battiti给出的一种考虑特征之间相关性的方法，此种方法需要预先指定与特征冗余程度有关的参数。基于最小冗余最大相关（minimum redundancy maximum relevance，mRMR）算法[2]，使用互信息衡量特征的相关性和冗余度，并使用信息差和信息熵两个代价函数来寻找特征子集，但是计算速度比较慢，冗余度和相关性评价方法单一，也不能根据用户需求设置特征维度。基于条件互信息（conditional mutual information，CMI）算法[3]，融入聚类思想，其在特征选择过程中一直保持特征互信息不变。Fleuret提出基于条件互信息最大化选择（conditional mutual information maximization，CMIM）算法[4]，采取一种变通的方式，使用单个已选特征代替整个已选子集以估算条件互信息。另外还有双方联合信息（joint mutual information，JMI）方法[5]、双输入对称相关（double input symmetrical relevance，DISR）方法[6]、条件最大熵特征提取（conditional infomax feature extraction，CIFE）[7]以 及 ICAP（interaction capping）[7]方法等可以用来进行特征选择。然而，上述算法都是在全局范围内对数据进行操控，并且难以兼顾泛化性能、学习效率和降维性能。

近年来，有关人工神经网络的研究发展迅速，而在其实际应用中，大部分的神经网络模型是基于BP神经网络及其变化形式。BP算法虽然有神经网络的普遍优点，但存在如收敛速度慢、易陷入局部最优等问题[8]。针对这些问题，Wang等人通过揭示单层前向神经网络（single-layer feedforward neural network，SLFN）的极限学习机（extreme learning machine，ELM）[9]以及中心化的岭回归之间的关系，提出了SLFN的最小学习机（least learning machine，LLM）理论[10]。与BP算法相比，LLM算法具有较高的学习效率和较强的泛化性能，也适用于求解大规模样本问题。然而，在实际应用中发现一些输入样本并不能被准确地分配到相应的类别[11]，因此LLM算法仍然存在一些局限性。对LLM引入模糊隶属度，从而得到模糊最小学习机FUZZY-LLM的概念，使得不同的输入样本会对输出结果的学习产生不同的影响。

为了弥补传统特征选择算法难以兼顾泛化性能、学习效率和高辨识能力特征子集获取的不足，同时改进LLM算法存在的一些局限性，本文提出了一种新算法——基于双模糊信息的特征选择算法（feature selection algorithm based on doubly fuzziness information，FSA-DFI），其双模糊具体体现在FUZZY-LLM算法以及基于贡献率的模糊补充方法中。具体来说，首先将FUZZY-LLM作为一种训练样本方法运用于每个特征对其进行分类，此时即可得到第一种模糊信息；然后使用一种新的模糊隶属度函数将其映射到模糊子空间，即可得到每个特征对应的模糊隶属度集；接着利用模糊隶属度集和基于贡献率的模糊补充方法可得到第二种模糊信息，用这种模糊信息指导特征选择过程的进行，将贡献率高的特征加入最终的特征子集。

2 LLM与FUZZY-LLM

2.1 LLM

假定已有构造好的L个无限可微的核函数g(xi,θ1),g(xi,θ2),…,g(xi,θL)，L表示隐含层节点个数，其中θ1,θ2,…,θL表示核的L个不同的参数向量，例如ELM中的wi,bi。关于样本集D={xi,yi,i=1,2,…,N}中输入、输出样本的逼近问题，可用下述的岭回归实现：

式中，C为正则化参数，令H=[h1,h2,…,hN]T。其中，hi=[g(xi,θ1),g(xi,θ2),…,g(xi,θL)]，T=[t1,t2,…,tN]T。

根据文献[12]的数据中心化思想，式（1）对应的岭回归还可等价于下述中心化岭回归问题的解。即令，其中IN×N是对角元素值为1，其余元素为0的N×N单位矩阵，1∈RN为一个所有元素为实数1的列向量，可以看出LT=L。因此，式（1）的解为：

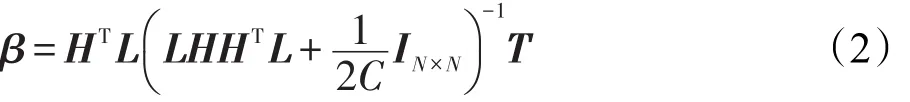
当C非常大时，β退化为：

其中，(LH)†为LH的伪逆（Moore-Penrose generalized inverse）。

LLM算法实现简单且学习效率非常高，能以较强的泛化能力实现函数逼近，也适用于求解大规模样本问题。LLM算法还可应用于回归问题及深度学习领域[13-14]。

2.2 FUZZY-LLM

在分类问题中，有些训练样本比其他样本更重要，重要的训练样本应该被正确地分类，而那些被噪声破坏的样本意义不大，可以被丢弃。换句话说，存在一个模糊隶属度si(0＜si≤1)和每个训练样本xi有关。在分类问题中，模糊隶属度si可以看成是相应的训练样本对某一类的重要程度。选择合适的模糊隶属度也是比较容易的。首先，选择σ＞0作为模糊隶属度较低的边界；其次，定义时间为主要属性，使得模糊隶属度si成为时间ti的函数：

其中，t1≤t2≤…≤tN是样本到达系统的时间。这里假设最后一个样本xN最重要，令sN=f(tN)=1，第一个样本x1最不重要，使得s1=f(t1)=σ。若要使得模糊隶属度与时间成线性关系，可以令

再应用边界条件得到：

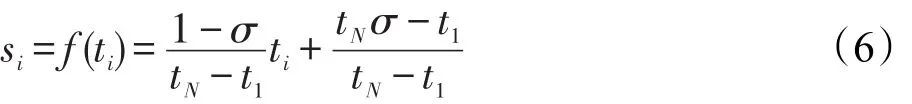
若要使得模糊隶属度为时间的二次函数，可以令

再应用边界条件可得：

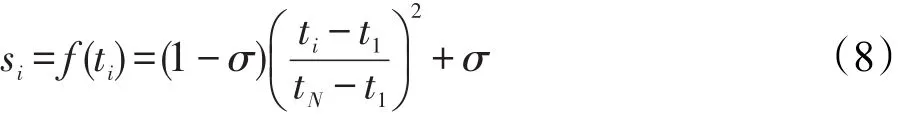
因此，对LLM进行模糊化后得到FUZZY-LLM。

考虑一个带有类标及模糊隶属度的训练样本集合D={xi,yi,si,i=1,2,…,N},yi∈{+1,-1}，yi表示类标，其中每个样本，模糊隶属度σ≤si≤1，σ表示一个大于0的较小值。前面提到，模糊隶属度si是相应的训练样本对某一类的重要程度，而参数是对错误的一个衡量，那么式子就是对不同权重错误的衡量。关于样本集D中输入、输出样本的逼近问题，可用下述的岭回归实现：

基于KKT理论，训练模糊LLM等价于解决下述对偶最优化问题：

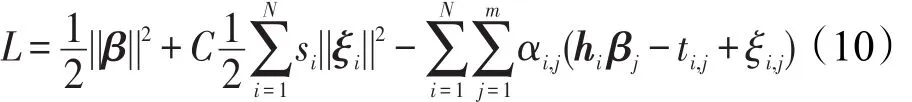
使用KKT相应的最佳性条件如下：

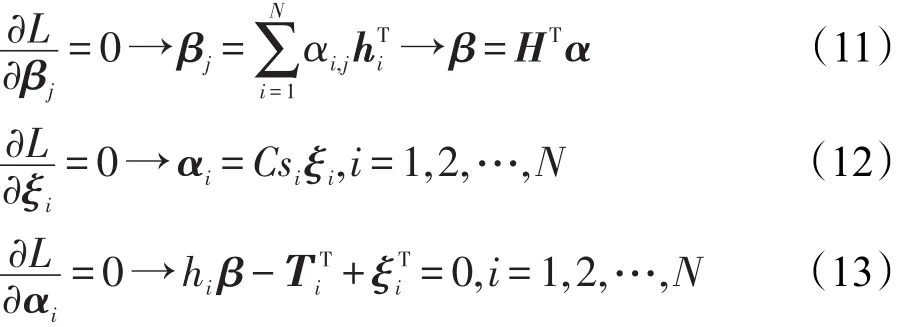
将式（11）和式（12）放入式（13）中替换，等式可以写成：

其中，T=[t1,t2,…,tN]T；模糊矩阵为：

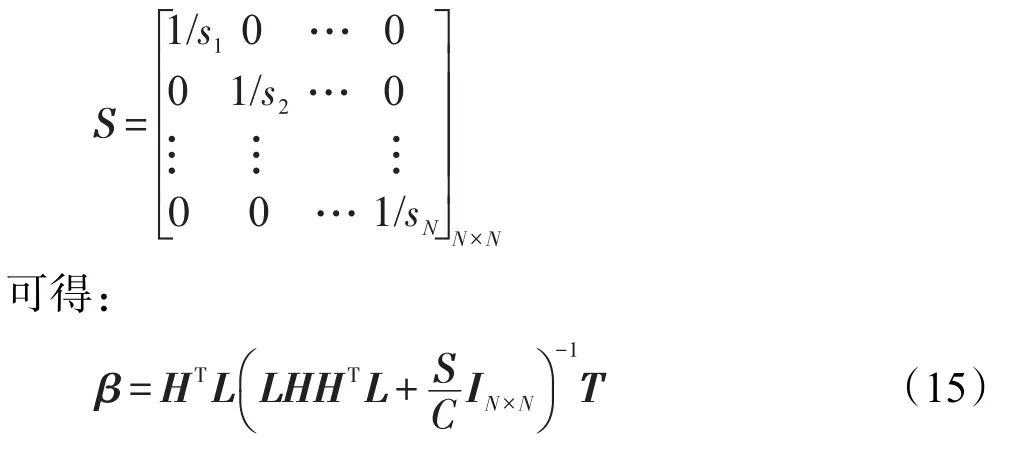
因此，不同模糊矩阵的输入样本点会对输出权重β的学习产生不同的影响。根据文献[15]，当训练样本个数较小时，FUZZY-LLM分类器的决策函数表达如下：

当训练样本个数较大时，对应的决策函数为：

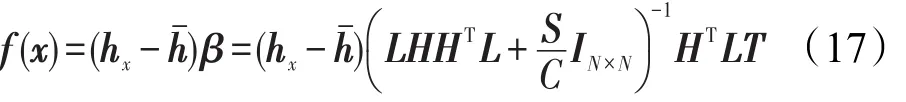
对于二分类问题，FUZZY-LLM只有一个输出节点且最终的决策值是。针对多分类问题，可以使用一对余方法（one versus rest，OVR）[16]，训练样本的预测类标就是有最高决策值的输出节点的序列数：

2.3 FUZZY-LLM实验研究

用UCI（http://archive.ics.uci.edu/ml/）中的7个数据集Wine、Cleveland、Ionosphere、Dermatology、Wdbc、Glass、Sonar进行实验，观察LLM和FUZZY-LLM算法性能的表现差异。在LLM、FUZZY-LLM中使用的激励函数形式是sigmoid型，隐含节点数为20，C为220，FUZZY-LLM中σ设为0.1。表1是两种算法测试准确率和训练时间的比较。可以看出，LLM和FUZZY-LLM的训练速度都很快，FUZZY-LLM的学习性能并不比LLM差。

在本文算法的双模糊信息中，将模糊隶属度的概念引入到LLM中即可得到FUZZY-LLM算法，那么使用该算法对输入样本进行训练即可得到第一种模糊信息。由于FUZZY-LLM学习性能很好，本文用这种新算法作为一种训练方法，即将这种方法用于每个特征的训练样本对其分类，得到所有分类器的决策值，用于后文将要介绍的模糊隶属度函数的求解。

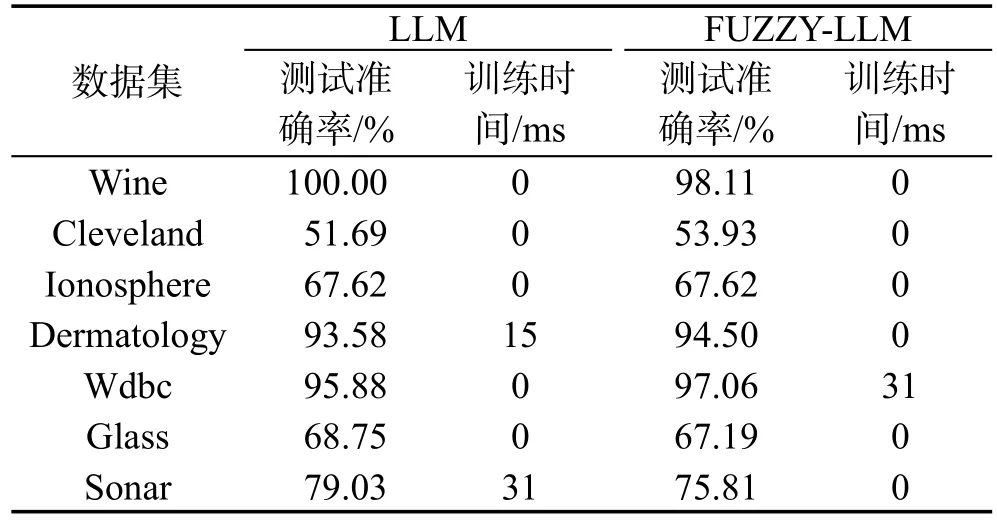
Table 1 Performance comparison of LLM and FUZZY-LLM表1LLM和FUZZY-LLM性能比较

3 特征选择

本章主要介绍本文所提出的第二种模糊，即使用基于贡献率的模糊补充方法来进行特征选择。首先介绍一种求样本模糊隶属度的新方法，通过该方法进而可以得到每个特征的模糊隶属度集；接着利用模糊隶属度集和基于贡献率的模糊补充方法可得到第二种模糊信息，用其可以指导特征选择过程的进行，以得到最佳特征子集。

3.1 模糊隶属度集

D中的训练样本根据类标排列如下：

对于有M类的样本集，用FUZZY-LLM方法对每个特征单独训练以获得每个样本对所属类的模糊隶属度。但是模糊隶属度不仅仅是由所属类的决策函数值决定，还和其他分类器的输出值有关。用xi,j表示样本xi的第j个特征，i=1,2,…,N。Ak(xi,j)∈[0,1]表示样本xi,j对所属第k类的模糊隶属度，fk(xi,j)表示由xi,j训练的第k个分类器的决策值，MXi,j,k表示由剩下的(K-1)个分类器获得的最大决策值：

则模糊隶属度函数中的自变量Fk(xi,j)表示如下：

模糊隶属度函数Ak(xi,j)的表达式可以计算如下：

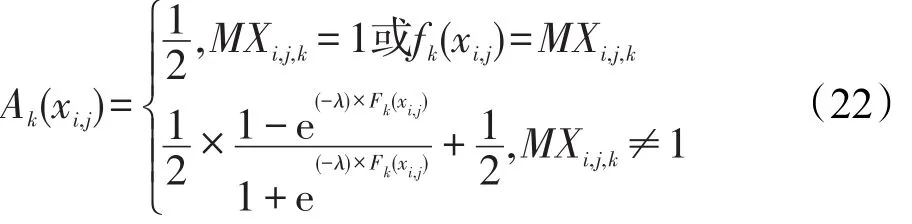
（1）当fk(xi,j)＞MXi,j,k时，表明样本对所在类的模糊隶属度比较高，Ak(xi,j)∈[0.5,1]。

（2）当fk(xi,j)＜MXi,j,k时，表明样本对所在类的模糊隶属度比较低，Ak(xi,j)∈[0,0.5]。

（3）当fk(xi,j)=MXi,j,k或MXi,j,k=1时，模糊隶属度为0.5，表明样本的分类情况不确定。另外，λ为可调参数，其对样本所属类别的模糊隶属度有较大影响。

现在将第k类中样本的模糊隶属度用一个集合表示，如式（23）所示：

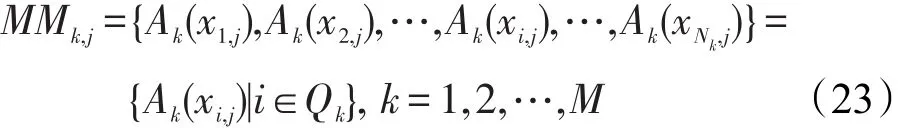
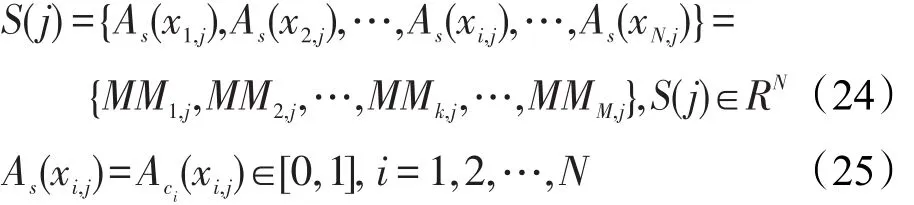
其中，ci表示样本xi,j所属类的类标。S(j)还可用下式定义：

其中，As(xi,j)表示xi,j对模糊集S的隶属程度。

为了客观地描述上述概念，图1描绘了第j个特征的模糊隶属度集S(j)与训练样本分布之间的关系。从图中可以看出，大部分样本都有较高的模糊隶属度（超过0.5），表明只考虑单个特征j时，能够很好地将这些样本区分开。而小部分样本有比较低的模糊隶属度（小于0.5），表明特征j并不能将它们正确区分开。S(j)关注的是与每个样本有关的局部特性。

模糊隶属度集S(j)的基数就是模糊隶属度集中元素累加之和，表示如下：

Fig.1 Relationship betweenS(j)and distribution of training patterns图1 S(j)与训练样本分布之间的关系

基数值|S(j)|主要是用来直观地评判一个特征的分类能力。若S(j)中绝大部分样本As(xi,j)的值都接近于1，则|S(j)|的值也比较大，就可以得出这一特征中训练样本的分类是比较正确的，由此可推出此特征的分类性能相对较高。而若|S(j)|的值比较低，也可说明其中很多样本都被分错，则此特征的分类性能较差。基数|S(j)|注重于对特征分类能力的整体评判。

3.2 基于贡献率的模糊补充方法

3.2.1 模糊域中相关定义

定义1两个模糊隶属度集合S(j)和S(q)的并集可以用S-norm[17]来定义，这里采用S3(A,B)=max(A,B)形式如下（http://www.nicodubois.com/bois5.2.htm）：

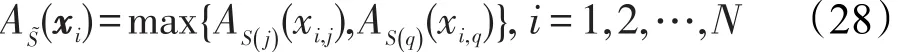
定义2(S(j)|-|S(q))两个特征模糊隶属度集合的差值定义如下[18]：

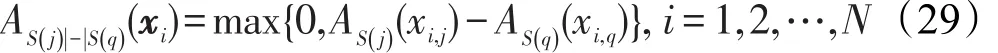
定义3(G(t))让表示被选上的t个特征的集合，G(t)表示包含在F(t)中所有特征的模糊隶属度集合的并集，其提供了一种近似方法去评估在第t次迭代中已选特征所获得的数据覆盖的质量：

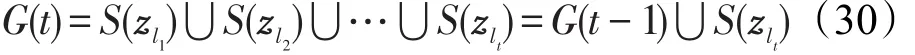
定义4(ES(zlt))若是在第t次迭代中的一个候选特征。表示特征和G(t-1)有关的额外贡献，是由提供的隶属度的剩余部分，G(t-1)表示在迭代中累积的并集。候选特征的额外贡献可用下式表达：

3.2.2 基于贡献率的模糊补充方法描述

在已选择第一个特征后，进行如下算法1过程：

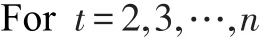
（2）选择特征判定条件：

基于贡献率的模糊补充特征方法能够促进特征之间的合作，确保新加入进来的特征具有补充意义。换句话说，新加入进来的特征能够为已选特征子集带来更高的模糊隶属度，而不是被之前已经选择出来的特征所完全覆盖。

3.3 FSA-DFI算法过程描述

本文提出了一种基于双模糊信息的特征选择新算法FSA-DFI。首先将FUZZY-LLM作为一种训练样本方法运用于每个特征对其进行分类得到第一种模糊信息；然后使用一种新的模糊隶属度函数得到每个特征对应的模糊隶属度集，最后使用模糊隶属度集和基于贡献率的模糊补充方法得到第二种模糊信息，用这种模糊信息指导特征选择过程的进行以得到最佳特征子集。若初始特征集合，n表示特征总数。本文算法步骤描述如下：

（1）初始化，定义初始模糊隶属度并集G(0)=∅,初始已选特征子集F(0)=∅，设定阈值E，设定可调参数λ。

（2）计算特征的模糊隶属度集，根据前述3.1节的式（20）～（24），计算特征集fs中每个特征的模糊隶属度集合S(zj),j=1,2,…,n。

（3）选择第一个特征，计算所有特征的模糊隶属度集基数，选择使得基数最大的特征：

（4）进行3.2.2小节中算法1的过程。

（5）输出最后被选择出来的特征集合。

3.4 FSA-DFI算法结束条件

将FSA-DFI算法应用在Wine数据集上，观察随着特征数目变化，分类精度和贡献率的变化情况。这里数据集划分为训练和测试部分（70%，30%），产生的特征子集通过KNN1分类器进行评估，阈值E设为0.1%。图2展示了被选择特征数目相对应的分类精度变化和贡献率的变化。贡献率一开始呈指数下降，而分类精度呈上升趋势后趋于稳定。阈值E作为算法结束条件，获得了9个特征，分类精度达到稳定值98.11%。

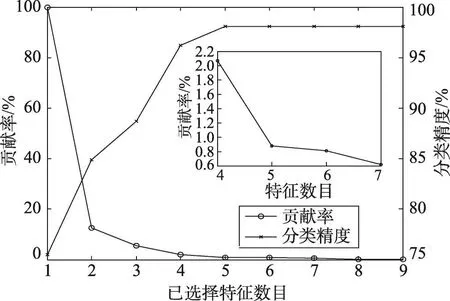
Fig.2 Evolution of contribution rateand classification rate versus number of selected features图2 被选择特征数目相对应的分类精度变化和贡献率的变化

4 实验研究与结果分析

4.1 实验数据集及实验平台简介

本文采用9个来自UCI的真实数据集进行实验，如表2所示。为避免结果的偶然性，对数据集随机抽取其中的70%作为训练样本，剩下的30%作为测试样本并进行10重交叉验证。特征选择结束后得到的特征子集使用KNN1分类器对其进行测试，得到最终的实验结果。

Table 2 List of datasets表2 数据集列表

实验平台：所有数据集在Intel Core i3-3240×2 CPU，主频为3.4 GHz，内存为4 GB，编程环境为Matlab2013a上进行仿真实验。

4.2 参数设置

（1）经过实验发现，式（22）中的参数λ在{1.0,1.5,2.0,2.5,3.0,3.5}中取值。这里选取3个数据集（Iris、Vehicle、Cleveland）观察λ对本文算法FSA-DFI泛化性能的影响，如图3所示，可发现在这3个数据集中，该参数是比较敏感的。

（2）算法中的阈值E从{0.1,0.2,…,1.0}中选择。E的值越小，表明选择的特征数目越多，降维程度越低，但能获得更高的测试准确率，反之亦然。

（3）FUZZY-LLM算法中正则参数C取值为220，隐含层节点数L取为20，算法最常用的激励函数形式为sigmoid型。

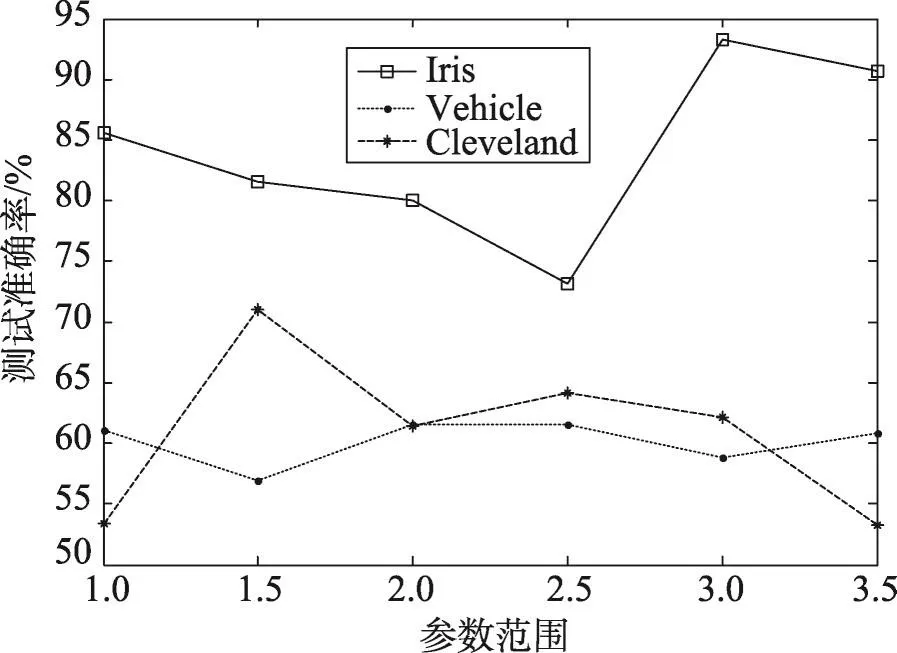
Fig.3 Effect of parameterλon accuracy of FSA-DFI algorithm图3 参数λ对FSA-DFI算法准确率的影响

4.3 评价指标

实验主要以测试准确率、降维程度(DR)和特征选择时间作为主要评价指标。其中，测试准确率是由10次随机划分所得准确率求均值得到，降维程度计算如下：

4.4 算法性能比较分析

本文的对比实验分为两部分：第一部分9组实验是对不同特征选择方法的泛化性能进行比较分析，与FSA-DFI算法进行比较的有CMIM[4]、JMI[5]、DISR[6]、CIFE[7]、ICAP[7]、MIFS[1]、CMI[3]、mRMR[2]算法，实验结果如表3所示。为方便比较，使得CMIM、JMI、DISR、CIFE、ICAP、MIFS、CMI和mRMR这几种算法最终选择的特征数目和本文算法FSA-DFI相同，即降维程度相同。表3中第二列是数据集在不同特征选择算法中所选择的特征数目。这些算法运行效率都很高，运行时间几乎为0，不进行比较。

第二部分9组实验是在本文的特征选择算法中采用不同训练方法进行比较的结果，与FUZZY-LLM方法进行比较的是 SVM[19]、LS-SVM[20]、FSVM[21]和LLM。其中，SVM、LS-SVM和FSVM的核函数是高斯RBF形式，如式（34）所示：

Table 3 Evaluation of test accuracy表3 测试准确率对比

SVM、LS-SVM、FSVM实验中正则参数C设为220，σ为1，参数λ值同FUZZY-LLM；FSVM中模糊隶属度si的计算同FUZZY-LLM，FSVM中SMO（sequential minimal optimization）算法的参数TolKKT为0.001，MaxIter为 15 000，KKTViolationLevel为 0，KernelCacheLimit为5 000。LLM方法中所有参数同FUZZY-LLM。实验结果如表4～表6所示，最优结果都用粗体标出。

从表3中可以看出，本文所提出的FSA-DFI算法泛化性能很高，其中在 Wdbc、Wine、Vehicle、Cleveland、Glass这5个数据集上具有最高的测试准确率，在其他几个数据集上也具有不错的性能。

从表4～表6中可以看出，本文提出的训练方法FUZZY-LLM 在 Heart、Wine、Cleveland、Ionosphere、Wdbc和Glass这6个数据集中都具有很高的准确率，而且在Cleveland和Glass这两个数据集中，本文算法的准确率要远高于SVM及其延伸算法。另外，在Heart、Wine、Iris、Cleveland、Ionosphere、Wdbc、Vehicle和Glass这8个数据集中，本文算法时间花费很少，可见其学习效率非常高，同时在这些数据集中也能保持不错的降维效果。同FUZZY-LLM相比，SVM算法通过牺牲学习效率以换取较高的测试准确率；LS-SVM算法也是通过牺牲准确率以换取较高的降维性能；而FSVM和LLM的总体性能也不如FUZZYLLM。在大规模数据集Wdbc、Vehicle和Segment中，相比于其他算法，采用FUZZY-LLM这种训练方法的效率依然很高，可见该算法可以很好地解决大规模数据集的分类问题。总之，本文算法既能得到很好的泛化能力，又能获得不错的降维效果，同时还具有非常高的学习效率，三者兼顾，还可以用于解决大规模数据集的分类问题。

Table 4 Comparison results of different training methods in Iris、Wine and Glass datasets表4 在Iris、Wine和Glass数据集中采用不同训练样本方法的比较结果

Table 6 Comparison results of different training methods in Wdbc、Vehicle and Segment datasets表6 在Wdbc、Vehicle和Segment数据集中采用不同训练样本方法的比较结果

5 实际问题实验探究

本文算法FSA-DFI将在4个真实存在的高维生物医学数据集上进行测试，如表7所示。其中，Leukemia和Colon数据集取自于http://datam.i2r.a-star.edu.sg/datasets/krbd/index.html，SRBCT和DLBCL数据集取自于http://www.gems-system.org/，这些数据集都是基因表达数据。

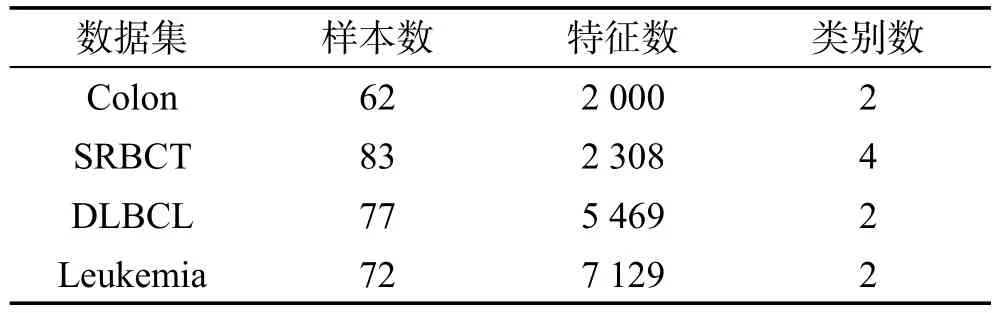
Table 7 List of high dimensional datasets表7 高维数据集列表

Colon数据集的样品是患者体内取出后20 min内在液氮中快速冷冻的结肠腺癌样品，其包括22个正常（标为“positive”）和40个肿瘤样品（标为“negative”）,每个样品有 2 000 个基因；Small，round blue cell tumors(SRBCT)of childhood，小圆形蓝色肿瘤数据集有83个样品，每个样品有2 308个基因，分为EWS、RMS、BL、NB这4类；Diffuse large b-cell lymphomas(DLBCL)and follicular lymphomas，弥漫性大b细胞淋巴瘤和滤泡性淋巴瘤有72个样品，每个样品有5 469个基因，分为DLBCL和FL这两类；Leukemia数据集取自于Golub报道的白血病患者样品的集合，数据集由72个样品组成，包含对应于来自骨髓和外周血的急性淋巴母细胞性白血病（ALL）的25个样品和急性髓细胞性白血病（AML）的47个样品，每个样品测量超过7 129个基因。

Colon、SRBCT、DLBCL和Leukemia数据集经过算法FSA-DFI测试后选择出来的特征数目依次是8、12、7、3。从表8可知，与传统特征选择方法相比，本文算法FSA-DFI在高维数据集中的分类精度依然很高。从图4和图5可得，与现存的其他分类方法相比，本文所提出的基于分类方法FUZZY-LLM所进行的特征选择算法在应用到实际的生物医学数据集问题中依然能够获得很高的泛化性能和学习效率。另外，基于这几种分类方法进行特征选择后得到的降维程度都接近100%，这里不予表示。FSA-DFI算法应用在Colon、SRBCT、DLBCL和Leukemia数据集中的降维度分别为99.59%、99.47%、99.87%、99.96%。因而可得，本文所提出的基于分类方法FUZZY-LLM所进行的特征选择算法FSA-DFI在应用到实际的高维生物医学数据集问题中依然能够兼顾泛化性能、降维程度以及学习效率。

6 结束语

本文提出了一种基于双模糊信息的特征选择新算法FSA-DFI，该算法能够在获取高辨识能力特征子集的同时获得很好的泛化性能，最突出的特点就是学习效率高，甚至在许多高维数据集中能获得比较优良的性能，因此可以很好地解决高维数据集、大规模数据集的分类问题。该算法的双模糊具体体现在FUZZY-LLM算法以及基于贡献率的模糊补充方法中。具体来说，首先将FUZZY-LLM作为一种训练样本方法运用于每个特征对其进行分类，此时即可得到第一种模糊信息；然后使用一种新的模糊隶属度函数得到每个特征对应的模糊隶属度集，第二种模糊信息是从模糊隶属度集和基于贡献率的模糊补充方法中得到的，用其可以指导特征选择过程的进行，以得到最佳特征子集，这种方式加强了特征间的协作关系，从而得到具有最小冗余最大相关性的特征子集。

Table 8 Comparison results of different feature selection methods in Colon,SRBCT,DLBCLand Leukemia datasets表8 在Colon、SRBCT、DLBCL和Leukemia数据集中应用不同特征选择方法的比较结果

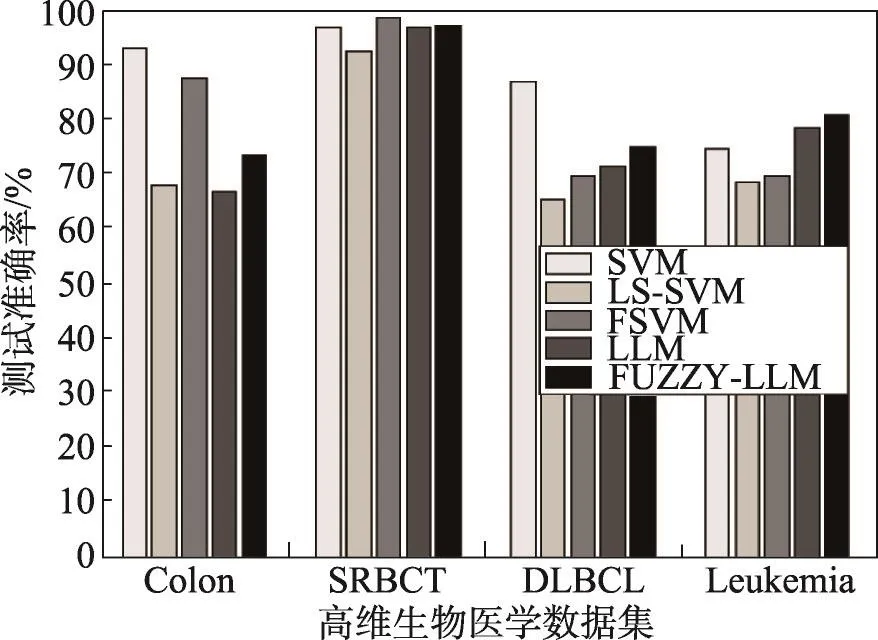
Fig.4 Comparison of test accuracy results using different classification methods in Colon,SRBCT,DLBCL and Leukemia datasets图4 在Colon、SRBCT、DLBCL和Leukemia数据集中采用不同分类方法测试准确率的比较

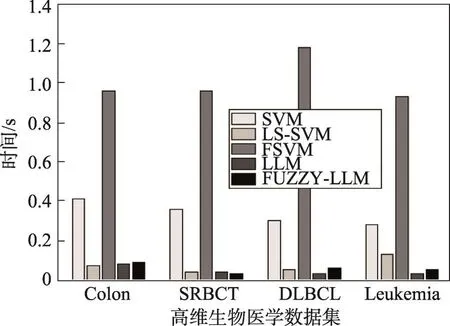
Fig.5 Comparison of feature selection time using different classification methods in Colon,SRBCT,DLBCL and Leukemia datasets图5 在Colon、SRBCT、DLBCL和Leukemia数据集中采用不同分类方法特征选择时间的比较

[1]Battiti R.Using mutual information for selecting features in supervised neural net learning[J].IEEE Transactions on Neural Networks,1994,5(4):537-550.

[2]Zhang Ning,Zhou You,Huang Tao,et al.Discriminating between lysine sumoylation and lysine acetylation using mRMR feature selection and analysis[J].PLOS One,2014,9(9):e107464.

[3]Sotoca J M,Pla F.Supervised feature selection by clustering using conditional mutual information-based distances[J].Pattern Recognition,2010,43(6):2068-2081.

[4]Fleuret F.Fast binary feature selection with conditional mutual information[J].Journal of Machine Learning Research,2004,5(3):1531-1555.

[5]Kerroum M A,Hammouch A,Aboutajdine D.Textural feature selection by joint mutual information based on Gaussian mixture model for multispectral image classification[J].Pattern Recognition Letters,2010,31(10):1168-1174.

[6]Bennasar M,Hicks Y,Setchi R.Feature selection using joint mutual information maximisation[J].Expert Systems with Applications,2015,42(22):8520-8532.

[7]Brown G,Pocock A,Zhao Mingjie,et al.Conditional likelihood maximisation:a unifying framework for information theoretic feature selection[J].Journal of Machine Learning Research,2012,13(1):27-66.

[8]Jing Guolin,Du Wenting,Guo Yingying.Studies on prediction of separation percent in electrodialysis process via BP neural networks and improved BP algorithms[J].Desalination,2012,291(14):78-93.

[9]Huang Guangbin,Zhou Hongming,Ding Xiaojian,et al.Extreme learning machine for regression and multiclass classification[J].IEEE Transactions on Systems,Man&Cybernetics:Part B Cybernetics,2012,42(2):513-529.

[10]Wang Shitong,Chung F L.On least learning machine[J].Journal of Jiangnan University:Natural Science Edition,2010,9(5):505-510.

[11]Zhang W B,Ji H B.Fuzzy extreme learning machine for classification[J].Electronics Letters,2013,49(7):448-450.

[12]Zhang Changshui,Nie Feiping,Xiang Shiming.A general kernelization framework for learning algorithms based on kernel PCA[J].Neurocomputing,2010,73(4/6):959-967.

[13]Wang Shitong,Chung F L,Wu Jun,et al.Least learning machine and its experimental studies on regression capability[J].Applied Soft Computing,2014,21(8):677-684.

[14]Wang Shitong,Jiang Yizhang,Chung F L,et al.Feedforward kernel neural networks,generalized least learning machine,and its deep learning with application to image classification[J].Applied Soft Computing,2015,37(C):125-141.

[15]Huang Guangbin,Zhu Qinyu,Siew C K.Extreme learning machine:theory and applications[J].Neurocomputing,2006,70(1/3):489-501.

[16]Student S,Fujarewicz K.Stable feature selection and classification algorithms for multiclass microarray data[J].Biology Direct,2012,7(1):33.

[17]Azadeh A,Aryaee M,Zarrin M,et al.A novel performance measurement approach based on trust context using fuzzy T-norm and S-norm operators:the case study of energy consumption[J].Energy Exploration&Exploitation,2016,34(4):561-585.

[18]Dereli T,Baykasoglu A,Altun K,et al.Industrial applications of type-2 fuzzy sets and systems:a concise review[J].Computers in Industry,2011,62(2):125-137.

[19]Chang C C,Lin C J.LIBSVM:a library for support vector machines[J].ACM Transactions on Intelligent Systems and Technology,2011,2(3):389-396.

[20]Suykens J A K,Gestel T V,Brabanter J D,et al.Least squares support vector machines[J].Euphytica,2002,2(2):1599-1604.

[21]Lin Chunfu,Wang Shengde.Fuzzy support vector machines[J].IEEE Transactions on Neural Networks,2002,13(2):464-471.

附中文参考文献：

[10]王士同,钟富礼.最小学习机[J].江南大学学报:自然科学版,2010,9(5):505-510.

Feature SelectionAlgorithm Based on Doubly Fuzziness Information*

LI Sushu+,WANG Shitong,LI Tao

School of Digital Media,Jiangnan University,Wuxi,Jiangsu 214122,China

2016-10,Accepted 2016-12.

Based on the traditional feature selection algorithms,this paper proposes a new feature selection algorithm based on doubly fuzziness information(FSA-DFI).One fuzziness is involved in the fuzzified version of least learning machine(LLM),i.e.,FUZZY-LLM,and the other fuzziness is involved in the contribution-rate based fuzzy complementary method in which the features with high contribution rates may be finally selected.The proposed feature selection algorithm is built on the combination of FUZZY-LLM and the contribution-rate based fuzzy complementary method.Experiments indicate that the proposed feature selection algorithm has better classification accuracy,better dimension reduction and faster learning speed,in contrast to other comparative algorithms.

feature selection;doubly fuzziness;least learning machine;fuzzy membership degree;fuzzy complementary

+Corresponding author:E-mail:lss85318977@163.com

10.3778/j.issn.1673-9418.1610058

*The National Natural Science Foundation of China under Grant No.61170122(国家自然科学基金).

CNKI网络优先出版:2017-01-03,http://www.cnki.net/kcms/detail/11.5602.TP.20170103.1028.002.html

LI Sushu,WANG Shitong,LI Tao.Feature selection algorithm based on doubly fuzziness information.Journal of Frontiers of Computer Science and Technology,2017,11(12):1993-2003.

A

TP181

LI Sushu was born in 1993.She is an M.S.candidate at School of Digital Media,Jiangnan University.Her research interests include artificial intelligence and pattern recognition,etc.

李素姝（1993—），女，江苏南通人，江南大学数字媒体技术学院硕士研究生，主要研究领域为人工智能，模式识别。

WANG Shitong was born in 1964.He is a professor and Ph.D.supervisor at School of Digital Media,Jiangnan University,and the member of CCF.His research interests include artificial intelligence and pattern recognition,etc.

王士同（1964—），男，江苏扬州人，江南大学数字媒体技术学院教授、博士生导师，CCF会员，主要研究领域为人工智能，模式识别等。

LI Tao was born in 1990.He is an M.S.candidate at School of Digital Media,Jiangnan University.His research interests include artificial intelligence and pattern recognition,etc.

李滔（1990—），男，四川绵阳人，江南大学数字媒体技术学院硕士研究生，主要研究领域为人工智能，模式识别等。