80 m球径螺栓球节点单层球面网壳强震失效机理

曹正罡，严佳川,周传波

(1. 结构工程灾变与控制教育部重点实验室(哈尔滨工业大学)，哈尔滨 150090；2. 哈尔滨工业大学 土木工程学院，哈尔滨 150090；3. 湖南大学 土木工程学院，长沙 410082)

80 m球径螺栓球节点单层球面网壳强震失效机理

曹正罡1,2，严佳川1,2,周传波3

(1. 结构工程灾变与控制教育部重点实验室(哈尔滨工业大学)，哈尔滨 150090；2. 哈尔滨工业大学 土木工程学院，哈尔滨 150090；3. 湖南大学 土木工程学院，长沙 410082)

为探究半刚性节点单层球面网壳在强震作用下的失效机理，以沈北新区80 m球径螺栓球节点单层球面网壳为研究对象，采用通用有限元软件ANSYS，引入节点试验和数值分析数据来模拟实际工程中螺栓球节点的抗弯性能，建立可考虑节点实际连接刚度的精细化数值模型，并进一步考虑局部杆件和节点加强、壳体外表面安装维护材料等不同结构条件的变化，在此基础上，对其开展强震作用下的失效机理研究.分析结果表明：沈北新区80 m球径螺栓球节点单层球面网壳的失效机理为局部节点瞬时大量破坏导致的结构动力失稳倒塌.局部加固网壳只能改善结构正常使用状态的各项响应指标，无法提高结构极限承载力.在现有结构表面安装维护面板，其各项响应指标(位移、支座反力等)皆明显增大，极限承载力下降57.1%，抗震能力明显降低.

半刚性节点；单层球面网壳；有限元模拟；时程分析；失效机理

单层球面网壳具有自重轻、受力合理、造型优美等一系列特点，常被应用于国家或地区的标志性建筑[1].当前单层球面网壳结构设计中，从安全性角度考虑，通常采用焊接球节点，此种节点焊接量大、工序复杂、施工质量无法保证，而传统的螺栓球节点标准化加工、装配方便、定位精准、外形优美，特别适用于单层通透性网格结构[2].在实际应用过程中，由于螺栓球节点锥头、套筒位置杆件截面的削弱，规程[3]中规定螺栓球节点假设为铰接节点，忽略其抗弯刚度，因此，中国仅在一些小跨度或作为维护结构的单层网壳中应用螺栓球节点[4].实际上螺栓球节点并非理想铰接节点，具有一定抗弯刚度，文献[5]研究表明，螺栓球节点球面网壳极限承载力最高可达刚接节点的98%，最低超过36%.对于螺栓球节点的抗弯性能早在20世纪90年代就有学者开始关注，英国研究人员对螺栓连接节点构造进行了总结和分类[6]，日本学者Shibata、Kato等[7-8]对螺栓球节点网壳进行了理论分析、数值模拟和试验研究，形成比较系统的分析方法，但对其失效机理的研究较少.国内学者范峰、支旭东等[9-11]进行考虑损伤累积、下部支承结构耦合效应和地震动空间变化性效应的单层球面网壳失效机理研究，其研究主要针对刚性节点.

本文针对单层螺栓球网壳示范性工程——沈阳沈北新区市民健身中心80 m球径单层球面网壳，对其在强震作用下的失效机理进行系统研究，同时探讨局部开洞以及洞口杆件加强和壳体外表面安装维护面板等对其极限承载力的影响规律.

1 工程概况及有限元模型

1.1 工程概况

沈北新区市民健身中心钢结构采用短程线型螺栓球节点单层球面网壳，球径80 m，矢高66.7 m，落地处跨度56 m，结构全貌见图1(a)，结构尺寸见图1(b)，采用材质为Q345B的无缝钢管，节点1 217个，均为传统螺栓球节点，支座采用成品固定铰支座，目前工程已经竣工.

1.2 有限元模型

利用ANSYS软件进行整体结构的模拟时，首先进行螺栓球与杆件连接处的自由度关系模拟，根据实际情况(图2(a)、2(b))，假设球节点和杆件之间没有相对轴向拉伸与压缩变形，仅考虑节点弯曲和扭转刚度影响，因此将其3个平动自由度直接耦合在一起，而3个转动自由度分别用3个弹簧单元(Combin39)来模拟[12]，依据每个圆形杆件的方位来建立局部坐标系，X方向弹簧模拟节点绕轴向的扭转刚度，Y、Z方向弹簧模拟节点的弯曲刚度，Combin39弹簧单元基本属性直接引入文献[12]中不同型号螺栓球节点弯矩-转角曲线，曲线中的极限弯矩或极限扭矩为实际节点螺栓屈服对应的内力.

图1 结构全貌及几何模型

采用Beam189梁单元模拟网壳中的杆件，其材料特性符合Q345B理想弹塑性模型假定.壳面节点所辖区域内重力荷载按等效原则以质量单元的形式集中在网壳节点上.按上述原则即可建立一个精细化的半刚性节点单层网壳的动力分析数值模型，选取EL-Centro地震动三向输入，采用时程分析法研究沈北市民健身中心网壳强震作用下的失效机理.同时考虑局部加固和安装维护面板后网壳的极限承载力变化规律，本文共建立3个分析模型，见表1.

图2 杆件与螺栓球节点的连接

类型简称结构特点实际工程模型模型1实际工程模型是表面不覆盖任何盖板,屋面恒荷载0.1kN/m2局部加固模型模型2局部加固模型是大小门周边节点采用刚性节点,屋面恒荷载0.1kN/m2加玻璃板模型模型3加玻璃面板模型,屋面恒荷载0.8kN/m2

2 研究方法及典型失效模式

2.1 研究方法

本文建立ANSYS有限元分析模型，采用多重响应的全荷载域动力时程分析法，考察网壳结构的强震失效机理.在分析中主要考察以下特征响应：

1)最大节点位移及其时程曲线.取结构振动幅度最大节点在整个动力时程内的最大振动幅值，宏观上体现结构的刚度水平，而通过节点振动时程曲线可判别节点振动是否平衡或结构已振动发散.

2)不同屈服程度杆件比例.结构中出现不同截面屈服程度的杆件比例，按照截面屈服程度不同定义为1P、3P、5P和8P，1P表示杆件截面上8个积分点中至少1个进入塑性，3P表示杆件截面上8个积分点中至少3个进入塑性，其余类推，宏观上体现结构的应力水平.

3)节点域受力特征.取内力最大节点域在整个动力时程内的最大值，判断螺栓球节点是否破坏.

4)支座反力.取反力最大支座在时程内的幅值，评价支座的安全性，判断结构失效时是否会发生整体倾覆.

2.2 典型失效模式

单层球面网壳在失效之前会出现各种不同的响应，文献[13]根据刚性节点球面网壳结构在地震作用下的特征响应总结和定义两种典型的失效模式，分别是动力失稳和强度破坏.

1)动力失稳.在这种破坏形式中，结构的几何非线性起到更为主要的作用，当各节点的振动平衡位置发生一定偏移后，结构即不能维持其总体平衡形状，失稳前内部塑性发展并不严重，结构位移较小.

2)强度破坏.结构随荷载幅值增大，要经受较大的反复塑性变形发展，结构刚度逐渐削弱,各节点的振动平衡位置发生越来越大的偏移，最后由于塑性损伤的过度累积导致结构再也不能维持其稳定振动状态而发生大塑性状态下的倒塌.

3 强震下网壳特征响应

3.1 节点位移

随着地震荷载幅值的不断增大，模型1和模型2中最大节点位移随之增长(见图3)，最终竣工网壳和局部加固网壳呈现倒塌趋势时的荷载均为700 gal，此时两者所对应的最大节点位移分别为0.925 m和0.412 m，加固后极限位移减小近55.5%，由此可知，局部节点加固虽然无法提高本球面网壳在强震作用下的承载力，但可有效限制网壳中最大节点位移.观察图3(b)，顶点位置节点位移随荷载幅值大致呈线性增长趋势，因此可以断定结构中发生最大位移节点位置出现在网壳薄弱区域(开洞处).若在现有竣工网壳表面安装维护面板(模型3)，其抗震能力急剧降低，当荷载幅值超过300 gal后结构中最大节点位移值开始发散，故仅从抗震角度考虑，在竣工网壳表面安装维护面板这一方案较为不妥.

为了确定3种模型在强震作用下的极限承载力，本文以模型1为例，研究其在不同峰值加速度地震动(EL-Centro)作用下的最大节点位移时程(图4)，研究发现，随着荷载幅值的增大，结构中节点偏离原平衡位置越来越远，当荷载幅值达到700 gal时，其位移阶跃到新的平台振动，并呈现发散迹象，结构存在倒塌趋势.综合分析节点位移时程曲线，可保守确定3个模型对应的极限承载力分别为700、700和300 gal.

3.2 塑性发展

图5(a)为沈北新区单层球面网壳(模型1)杆件进入塑性比例随荷载幅值变化的响应曲线，当荷载幅值小于500 gal时，结构中无杆件进入塑性，整个网壳处于弹性状态；荷载幅值超过500 gal后，杆件进入塑性的比例急剧增大，但总量较小，荷载幅值为700 gal时，网壳中杆件截面至少1个积分点进入塑性的比例为0.6%，而全截面进入塑性的比例仅为0.5%，由此可见网壳发生破坏时内部塑性发展不大，沈北网壳的破坏不具有强度破坏的典型特征.

图3 荷载幅值-节点位移曲线

图4 模型1最大节点位移时程曲线

局部加固网壳(模型2)和安装维护面板网壳(模型3)中杆件进入塑性比例随荷载幅值变化规律见图5(b)和5(c).模型2中的杆件在荷载幅值为400 gal时开始进入塑性，当荷载幅值达到700 gal时，网壳中杆件1P以上进入塑性比例为1.0%，全截面进入塑性比例为0.7%，相比模型1，各项比例值均有不同程度增大.究其原因，局部加固导致门柱附近节点刚度增加，相应杆件上分担的内力亦随之增大，故而相同荷载幅值作用下模型2中进入塑性杆件更多.模型3中的杆件从100 gal开始进入塑性，300 gal时，网壳中杆件1P以上进入塑性比例为0.44%，而全截面进入塑性比例仅为0.22%，该网壳破坏时杆件进入塑性比例更小.由上述现象可知，3种模型最终破坏模式都不具有强度破坏的典型特征.

图5 不同网壳进入塑性杆件比例

3.3 节点域内力

分析3种模型中螺栓球节点球端内力随荷载幅值的变化规律(扭矩和弯矩皆取绝对值)，见图6.模型1和模型3在常遇地震作用时有螺栓球节点球端达到极限扭矩，但达到极限弯矩时对应的荷载幅值不同，其中模型1中的节点400 gal开始达到极限弯矩，模型3则对应220 gal，由此可知，网壳表面安装维护面板会使节点域内力显著增大，造成大量节点因达到其极限扭矩、弯矩而破坏.模型2中的螺栓球球端扭矩维持在0.3～0.4 kN·m范围内，最大弯矩小于最大扭矩40 kN·m，因此局部加固的网壳直到发生结构倒塌之前无节点破坏.

基于上文的研究结果，进一步探讨3种模型中节点破坏比例和单个荷载步下网壳节点最大破坏比例随荷载幅值的变化规律.图7显示随着荷载幅值的增大，在接近极限荷载时，模型1和模型3中的节点破坏总数急剧增多，结构中发生大量节点破坏，综合以上分析结果可知，网壳中螺栓球节点破坏是探究网壳失效模式必须考虑的关键影响因素.

图6 球端力-荷载幅值曲线

图7 节点破坏个数-荷载幅值曲线

3.4 支座反力

从图8(a)可知，当荷载幅值不超过300 gal时，模型1中的最大支座反力与荷载幅值基本呈线性关系，随着荷载幅值的继续增大，结构中的最大支座反力呈现非线性变化，当达到极限荷载700 gal时，沈北单层球面网壳(模型1)中的最大支座反力为4 586.6 kN，随后最大支座反力急剧增大.模型3中支座反力变化规律与模型1相似，当达到极限荷载300 gal时，最大支座反力为3 726.8 kN，随后也是急剧增大，最终结构破坏.模型2的变化规律与前两种网壳不同，网壳直至破坏时最大支座反力与荷载幅值都呈现线性关系，支座反力无急剧增大现象，极限荷载时其最大支座反力为4 248.6 kN.

进行时程分析时，3种结构中支座部位都出现了不同大小的拔力，其中结构中最大支座拔力随荷载幅值的变化规律见图8(b)，3种模型达到各自极限荷载时，支座中出现拔力最大的是模型1，其值为3 510.9 kN，而图9则给出出现拔力支座个数随荷载幅值的变化规律，700 gal时，模型1中出现拔力的支座个数达到27个，接近总支座个数(51)的52.9%，且连片出现，因而结构有发生倾覆危险.模型3和模型2达到各自极限荷载时支座拔力分别为3 105.5 kN和2 781.4 kN，因此从网壳支座反力考虑，加固后的结构性能亦更优.

图8 荷载幅值-支座反力曲线

结合图9分析，3种结构从220 gal开始，单荷载步结构中出现拔力支座个数维持在较高的水平(35.3%以上)，因此针对此种单层球面网壳，必须考虑结构在地震作用下是否发生倾覆.

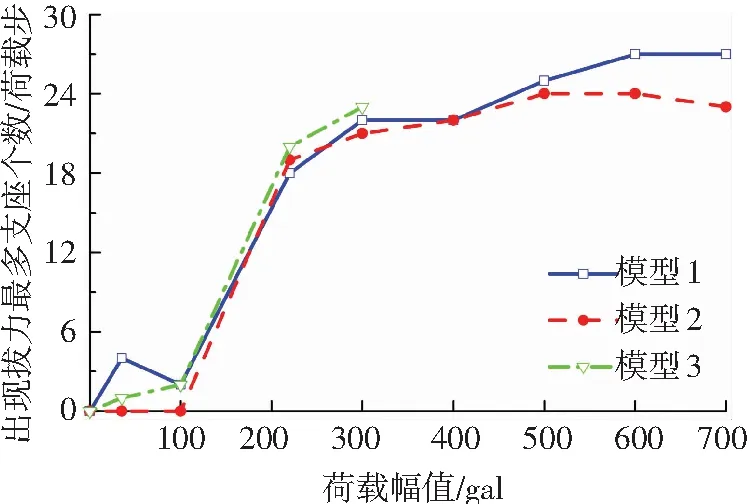
图9 单荷载步出现拔力支座个数-荷载幅值曲线

Fig.9 The number of bearings with pulling per load steps-acceleration amplitude

4 网壳失效机理

分析发现沈北单层球面网壳破坏前内部塑性发展并不严重，结构位移相对较小，结构破坏比较突然，其失效模式符合动力失稳的一般特征，但造成失稳的原因与通常意义的动力失稳不一样，下文将重点对模型1在破坏荷载作用时对应的时程过程来研究结构失稳原因.

由3.3节研究结论，选择网壳失效机理探索的切入点为结构中的节点，图10绘出模型1和模型2对应荷载幅值800 gal，模型3对应荷载幅值400 gal时节点破坏个数时程，3种网壳在最后破坏时，节点破坏个数发生阶跃，结构中发生瞬时大量节点破坏.

图10 节点破坏比例时程曲线

进一步研究模型1在极限荷载作用下破坏瞬间杆件和节点状态，分析发现在结构破坏瞬间，大门左侧局部区域大量杆件或者节点位移瞬间增大，见图11，结构发生破坏瞬间，在一个区域，大量节点发生破坏，与结构局部失稳的位置基本重合，由此可知瞬间大量节点破坏是导致结构失稳的直接原因.

在上文分析基础上，研究结构破坏与杆件塑性发展的关系，图12呈现了结构破坏瞬间模型1中杆件的塑性发展，结构在破坏瞬间，无大量杆件进入塑性，进入塑性杆件总量所占比例很小，塑性杆件位于第16～20环，大门左侧，这是因为该位置为网壳中杆件截面变化位置，且处于X轴方向，X向地震动贡献大，网壳中杆件内力较大.破坏瞬间，仅新增少量塑性杆件，新增塑性杆件位于节点破坏区域上方，这主要是因为瞬时节点大量破坏，失效节点区域杆件内力减小，导致失效区域附近杆件内力增大,部分杆件进入塑性.

沈北螺栓球节点单层球面网壳的失稳破坏是由于网壳局部区域瞬时大量节点受弯或者受扭破坏(图11)，节点瞬间破坏数为总节点的2.6% (图10)，导致壳面大门左侧区域凹陷，局部承载力丧失，最终网壳动力失稳破坏.

图11 不同时刻模型1破坏节点位置

图12 不同时刻模型1杆件塑性发展

5 结 论

1)沈北新区单层球面网壳的极限荷载为700 gal，网壳发生破坏时内部塑性发展不大，破坏瞬间大量节点发生破坏，其失效机理为局部节点瞬时大量破坏导致的结构动力失稳倒塌.

2)局部加固网壳的极限荷载为700 gal，加固后极限位移减小近55.5%，极限荷载时杆件进入塑性比例增加56.5%，最大支座反力减小7.4%，局部加固能改善结构正常使用状态的各项响应指标，无法提高结构极限承载力.

3)在现有结构表面安装维护面板，其极限荷载为300 gal，各项响应指标(位移、支座反力等)均大于竣工网壳，极限承载力下降57.1%，抗震性能明显降低.

[1] 王策, 沈世钊. 单层球面网壳结构动力稳定分析[J]. 土木工程学报, 2000, 33(6): 17-24.

WANG Ce, SHEN Shizhao. Analysis on stability of single layer spherical lattice shell[J]. China Civil Engineering Journal, 2000, 33(6): 17-24.

[2] 刘才玮, 张毅刚, 吴金志. 考虑螺栓球节点半刚性的网格结构有限元模型修正研究[J]. 振动与冲击, 2014, 33(6): 35-43.

LIU Caiwei, ZHANG Yigang, WU Jinzhi. Finite element model updating of single-layer latticed cylindrical shell in consideration of the semi-rigid characters of bolt-ball joint[J]. Journal of Vibration and Shock, 2014, 33(6): 35-43.

[3] 空间网格结构技术规程：JGJ 7—2010[S]. 北京:中国建筑工业出版社, 2010.

Technical specification for space frame structures: JGJ 7—2010[S]. Beijing: China Building Industry Press, 2010.

[4] 赵宪忠, 沈祖炎, 陈以一，等. 上海东方明珠国际会议中心单层球网壳整体模型试验研究[J]. 建筑结构学报, 2000,21(3): 16-22.

ZHAO Xianzhong, SHEN Zuyan, CHEN Yiyi. Experimental research on single layer spherical lattice shell of Shanghai Oriental pearl international conference center[J]. Journal of Building Structures, 2000, 21 (3): 16-22.

[5] 曹正罡, 范峰, 马会环，等. 螺栓球节点试验及在单层网壳结构中的应用性[J]. 哈尔滨工业大学学报, 2010,42(4):525-530.

CAO Zhenggang, FAN Feng, MA Huihuan，et al. Experiment of bolt-ball joint and its applicationin single-layer reticulated shells[J]. Journal of Harbin Institute of Technology, 2010, 42(4): 525-530.

[6] CHENAGHLOU M R. Semi-rigidity of connection in space structure[D]. Guildford: University of Surrey, 1997.

[7] SHIBATA R, KATO S, YAMADA S. Experimental study on the ultimate strength of single-layer reticular domes[C]//Proceeding of the Fourth International Conference of Space Structures. UK Surrey: University of Surrey, 1993: 387-395.

[8] KATO S, MUTOH I, SHOMURA M. Collapse of semi-rigidly jointed reticulated domes with initial geometric imperfections[J]. Journal of Constructional Steel Research, 1998, 48: 145-168.

[9] 支旭东, 聂桂波, 范峰,等. 大跨度单层球面网壳的损伤模型及强震失效[J]. 哈尔滨工业大学学报, 2009,41(8): 6-11.

ZHI Xudong, NIE Guibo, FAN Feng. Damage model and failure mechnism of long-span single layer spherical lattice domes under earthquakes[J]. Journal of Harbin Institute of Technology, 2009,41(8): 6-11.

[10]于志伟, 支旭东, 范峰,等. 单层球面网壳与支承结构整体强震失效特征[J]. 哈尔滨工业大学学报, 2010,42(10):1519-1523.

YU Zhiwei, ZHI Xudong, FAN Feng, et al. Failure behavior of reticulated domes with substructures subjected to the severe earthquake[J]. Journal of Harbin Institute of Technology, 2010,42(10): 1519-1523.

[11]王燕丽. 单层球面网壳考虑地震空间相关性效应的参数分析研究[D]. 哈尔滨:哈尔滨工业大学, 2013.

WANG Yanli. Parameter analysis of seismic spatial correlation effects on single-layer reticulated domes[D].Harbin: Harbin Institute of Technology, 2013.

[12]马会环. 半刚性节点单层网壳稳定性能及设计方法研究[D]. 哈尔滨: 哈尔滨工业大学, 2012.

MA Huihuan. Stability analysis of semi-rigidity single layer spherical reticulated shells and design method research [D]. Harbin: Harbin Institute of Technology, 2012.

[13]ZHI X, FENG F, SHEN S. Failure mechanisms of single-layer reticulated domes subjected to earthquakes[J]. Journal of the International Association for Shell and Spatial Structures, 2007, 48(1): 29-44.

(编辑赵丽莹)

Failuremechanismofan80metersspansingle-layerreticulateddomewithbolt-balljointssubjectedtosevereearthquakes

CAO Zhenggang1,2, YAN Jiachuan1,2,ZHOU Chuanbo3

(1.Key Laboratory of Structures Dynamic Behavior and Control (Harbin Institute of Technology), Ministry of Education, Harbin 150090, China; 2. School of Civil Engineering, Harbin Institute of Technology, Harbin 150090, China; 3. School of Civil Engineering, Hunan University, Changsha 410082, China)

Taking an 80-meters-span singer-layer reticulated dome which have been constructed in the Shenbei New District as an example, the failure mechanism of the singer-layer reticulated dome under severe earthquakes were analyzed with the FE software ANSYS. Based on the data of the numerical analysis and the test of the joints, the bending performance of bolt-ball joints were obtained and introduced into the numerical analysis considering the joint stiffness. Different structure models were established to investigate the effect of structure model changes, including the strengthening the local members and joints and installing maintenance materials on the surface of the structure. The analysis indicates that the failure mechanism of this structure is the collapse due to the dynamic instability of the structures while the local joints are damaged instantaneously and massively. The reinforcement of the reticulated dome merely improves the behavior of the structures in normal service condition, but it cannot improve the ultimate bearing capacity. The seismic response including displacement and support reaction increase obviously by installing maintenance panels on the existing surface, while the ultimate bearing capacity of the structures reduces by 57.1% and its seismic capacity decreases largely.

semi-rigid joint; single-layer reticulated shell; finite element simulation; time-history analysis; failure mechanism

10.11918/j.issn.0367-6234.201603155

TU393.3

A

0367-6234(2017)12-0039-06

2016-03-31

国家自然科学基金面上项目(51378147);

国家自然科学基金青年基金(51308155)

曹正罡(1975—)，男，副教授，博士生导师

周传波，hitzhoucb@163.com