无底柱分段崩落法不同放矿方式下崩矿步距研究

金爱兵，孙浩，孟新秋，高永涛，吴琼，张光

(北京科技大学 土木与资源工程学院，北京，100083)

无底柱分段崩落法不同放矿方式下崩矿步距研究

金爱兵，孙浩，孟新秋，高永涛，吴琼，张光

(北京科技大学 土木与资源工程学院，北京，100083)

以梅山铁矿为研究对象，在分段高度×进路间距为18 m×20 m的大结构参数下，设置不同的步距，分别采用无贫化放矿、低贫化放矿和现行截止品位放矿3种方式进行相似材料模拟实验。结合PFC2D数值模拟，分别从正面和侧面2个方向对矿石回收及废石混入进行模拟分析。研究结果表明：无贫化放矿、低贫化放矿和截止品位放矿3种出矿方式的最优崩矿步距分别为4. 5，3.8和3.8 m。无贫化放矿方式基本不破坏矿岩界面的完整性，减少矿岩的混杂机会，因而能最大限度地降低贫化；不同的放矿方式有不同最优放矿步距，当终止出矿时，步距较大，则混入废石主要来源于上部，正面残留较多；当步距较小时，正面废石会过早混入，整体回收率低；当步距适中时，正面废石和上部废石同时混入，回收效果较好。

无底柱分段崩落；放矿方式；崩矿步距；相似材料模拟；数值模拟

目前，在国内有85%的铁矿山在地下开采时采用崩落法开采，在国外，大约有25%的矿山采用崩落法开采[1]。由于崩落法采矿法具有覆岩下放矿的特点，采出矿石的损失与贫化都很大，加上采场结构参数不是最优及放矿管理不当，造成大量矿产资源浪费，直接导致矿山经济效益下降[2]。一条回采巷道通常要进行多次崩矿，对于当前步距崩落的矿石，其上部和正面是被废石包围的，在铲运机出矿的过程中，不同的结构参数可能产生不同情况的废石混入。正面废石可能早于上部废石混入矿石产生贫化，也可能晚于或与上部废石同时混入矿石。目前研究放矿的方法主要有室内相似材料模拟实验、现场原位实验和数值模拟实验3大类。在室内相似模拟实验中，主要针对对回收效果影响最大的3个因素(即进路间距、分段高度以及崩矿步距)进行研究[3−10]。现场原位实验能真实反应现场情况，但费时费力，一个实验从设计到完成可能需要若干年，周期较长，而且受现场爆破等生产条件影响较大[11]。随着计算机技术的发展，数值模拟计算方法得到越来越广泛的关注和使用[12−13]。颗粒流程序(PFC)是基于离散单元法对非连续介质进行研究的方法，既可以模拟圆形颗粒间的运动和相互作用，在研究非连续介质的力学问题方面有很大的优势，也可以模拟矿石颗粒的运移过程，因此，近年来在放矿领域得到广泛应用[14−19]。梅山铁矿为一大型缓倾斜极厚矿体，采用无底柱分段崩落法进行开采。实际生产段的进路间距×分段高度仍为 15 m×15 m，崩矿步距为2.4 m；现阶段正在−318 m水平进行现场原位实验，分段高度×进路间距为18 m×20 m，崩矿最大步距为2.8 m。但由于爆破效果不佳，极易造成大块堵塞现象；同时，梅山铁矿采用截止品位放矿方式进行出矿管理，贫化率较高，因此，有必要对不同放矿方式下最优崩落步距进行研究。无底柱分段崩落法放矿方式可分 3种：截止品位放矿、无贫化放矿和低贫化放矿。每种放矿方式都有其对应的最优崩矿步距。本文作者以梅山铁矿为研究对象，在确定分段高度和进路间距的前提下，通过相似材料模拟实验，研究崩矿步距及放矿方式对矿石回收率及贫化率的影响。在此基础上，采用PFC2D软件对其结果进行数值模拟分析，并与室内试验结果进行对比。

1 相似材料模拟实验

1.1 实验基本情况

试验采用的模型实体及装料情况如图1所示。模型相似比为1:100，分3个分段，每分段4～5个进路，分段高度×进路间距为18 m×20 m。模型高×宽×长为 1.0 m×0.25 m×1.0 m，进路宽×高为 5.4 cm×3.8 cm。

实验中所使用的松散材料应满足在放矿过程中不破碎，能长期保持原有物理力学性质，且矿石与废石的颜色有显著区别，易于分选。因此，在保证实验准确性的基础上，为方便矿岩分选，本次实验中废石采用品位为 0的大理石，矿石采用梅山的磁铁矿，矿石和废石粒径范围为5～10 mm，矿石密度kρ′为3.8 g/cm3，装填密度kρ为2.8 g/cm3，废石密度fρ′为2.20 g/cm3，装填密度fρ为1.4 g/cm3。化验所得磁铁矿平均品位为39.79%，近似为40%。

共设计3种不同贫化程度的放矿实验方案，停止出矿时当次矿岩品位分别为 C0=40%(无贫化)，CCj1=30%(低贫化)和 CCj2=25%(截止品位)，每个放矿口单次出矿200 g左右称量1次。为便于实际操作，将截止出矿品位换算成废石与矿岩质量比，换算结果如表1所示(如方案Ⅱ中，废石混入率为25%表示当次放出矿岩中废石占矿岩总质量25%时停止出矿)。

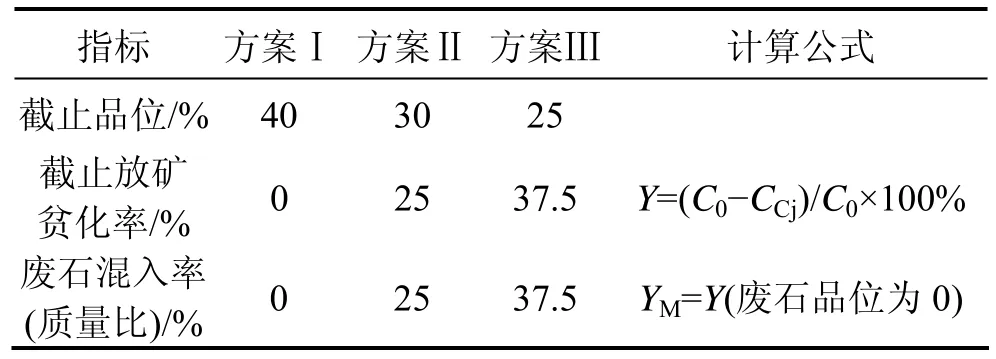
表1 指标换算Table 1 Indicators conversions

1.2 实验结果及分析

图1 相似材料实验Fig. 1 Similar material experiments

设置4，5，6和7 m这4种放矿步距，针对上述3种不同贫化程度的放矿方式，每种进行4次放矿实验，共计12次实验，以步距为6 m、采用截止品位方式放矿为例，分段放矿如图1所示。装矿前用隔板插入插槽隔开矿石和正面废石，装填到3个分段高度后抽出隔板，在矿岩上部继续装废石形成上部覆岩，装填结束后模型正视图如图1(a)所示。图1(b)，(c)和(d)所示分别为第1，2和3分段放矿结束时状况。

实验结果如表2和表3所示，其中：无贫化(a)和低贫化(a)分别表示相应实验中的第3分段截止出矿条件采用无贫化和低贫化的放矿方式；无贫化(b)和低贫化(b)均表示相应实验中的第3分段截止出矿条件采用截止品位放矿方式。

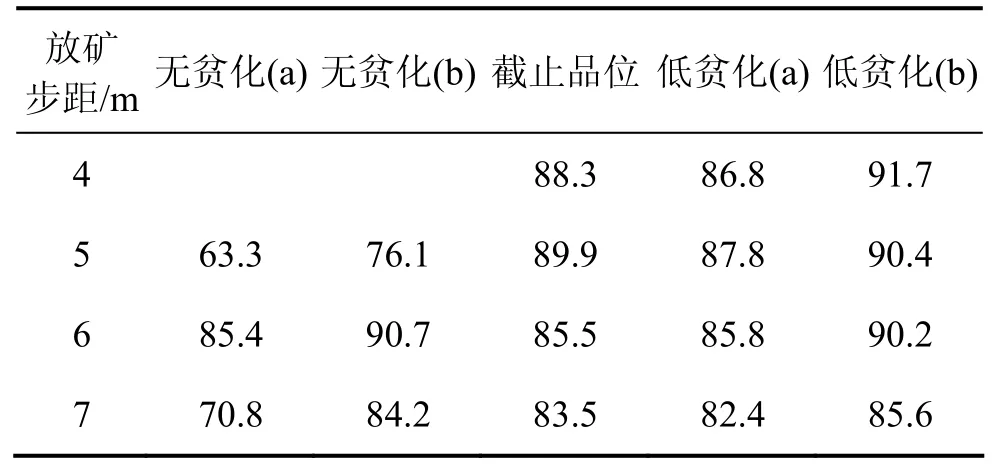
表2 回收率与步距关系Table 2 Relationship between recovery rate and caving steps%

表3 回贫差与步距关系Table 3 Relationship between caving steps and subtraction of recovery and dilution %

在放矿步距为5 m，以无贫化放矿方式进行回收的放矿实验操作过程中，当上部矿石离放矿口仍有一段距离时，正面废石已经开始混入，回收效果较差，由此推断放矿步距为4 m时这种情况会更早发生，回收效果会更差，因此，没有进行相关实验。

根据表2绘制总回收率随步距变化关系曲线，如图2所示。从图2(a)可以看出：在第3分段截止出矿条件分别采用各自的放矿方式进行时，无贫化放矿方式受步距影响非常大；在放矿步距为6 m时，3种放矿方式总回收率十分接近；在其他步距情况下，截止品位放矿回收率均大于低贫化放矿的回收率。从图2(b)可以看出：在第 3分段截止出矿条件均采用截止品位放矿方式进行时，无贫化放矿方式在放矿步距为5 m时总回收率依然很低，但在放矿步距为6 m时，其总回收率比其他2种放矿方式的高，在放矿步距为7 m时3种放矿方式总回收率相近。

图2 回收率随步距变化关系Fig. 2 Relationship between caving steps and recovery rate

图3 所示为回贫差随放矿步距的变化关系曲线。考虑到废石混入率这一回收指标，以回贫差作为衡量回收效果的标准。从图3可以看出：无论第3分段采用何种放矿方式作为截止出矿条件，无贫化、低贫化、截止品位3种放矿方式对应的回贫差都分别在放矿步距为6，5和5 m时最大，所以，3种放矿方式对应的最优放矿步距分别为6，5和5 m。采用低贫化出矿方式下，步距对回收率影响最小，而且在4个不同放矿步距下，低贫化放矿方式的回贫差均高于截止品位放矿方式的回贫差。

图3 回贫差随步距变化关系Fig. 3 Relationship between caving steps and subtraction of recovery and dilution

2 PFC数值模拟研究

颗粒流(PFC)作为一种特殊的离散元，主要用于研究岩石类材料基本特性、颗粒物质动力响应、岩石类介质破裂和破裂发展等基础性问题。因此，该方法非常适合研究崩落法条件下矿岩运移规律。本文作者采用PFC2D数值模拟软件分别就脊部残留和正面残留以及靠壁残留3个矿石残留体的回收情况及矿石回收过程废石混入情况进行研究。

2.1 模型建立

图4所示为模型示意图。其中，正面放矿模型与相似模拟实验的结构参数相对应，分3个分段，每个分段高度为18 m，上覆废石层厚度为18 m(图4(a))；端部放矿模型矿石层厚度为36 m，中间部分为脊部残留，最下部分为出矿进路(图 4(b))。其他结构参数如图4所示。PFC建模首先需要将建模所需细观力学参数与宏观试验参数匹配，即进行细观力学参数调试。本次模拟采用的细观力学参数如表4所示。其中，矿岩颗粒密度为实际矿岩散体的实体密度，孔隙率及摩擦因数分别通过装料情况和自然安息角计算获得，而墙体及矿岩颗粒的刚度则经反复调试后确定。当采用表4中所示法向和切向刚度时，数值实验所得物理力学参数与实际矿岩散体的宏观物理力学参数基本吻合。

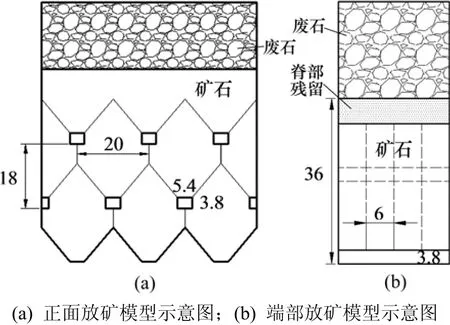
图4 模型示意图Fig. 4 Schematic diagrams of the model

表4 颗粒细观力学参数Table 4 Particle mesomechanics parameters

2.2 模拟过程及结果

采用Fish语言编写代码，第1分段放矿时固定边孔角及放矿口以下的颗粒，每隔一定步数统计落入放矿口区域内的矿岩平均品位，与设定的截止品位对比，之后删除落入放矿口内的颗粒，一旦平均品位小于截止品位即终止出矿。对于无贫化放矿，当落入放矿口内矿岩平均品位低于40%时，停止出矿。第1分段放矿完成之后解除下一分段颗粒的约束，重复上述操作进行下一分段放矿。

图5所示为其脊部残留回收数值模拟过程。无贫化放矿一旦遇到废石就停止出矿，矿岩界面的完整性基本不受破坏，在整个开采期间呈曲线状均匀下降，在出矿水平以上形成废石隔离层，能够隔离废石与矿石，大大减少矿岩混入的机会。放出体形态为近似椭球体。从图5可以看出：崩落矿石残留体的形态与放出体形态保持一致，上一分段脊部残留的矿石在下一分段能够很好地得到回收，从而使放矿取得良好的效果。因此，矿石残留体对于采用无贫化放矿取得良好放矿效果是极为重要的。

图5 脊部残留回收数值模拟过程Fig. 5 Numerical simulation of recycling processes of ridges residue

图6 所示为端部出矿的数值模拟过程。图中上层颗粒层表示上覆废石层，中间颗粒层表示脊部残留体，下层颗粒层表示当前分段未崩落矿体。由于第1步距的矿石正面为切割形成的自由面，不存在崩落的松散废石，所以，模拟过程以右墙替代，而第2步距的放矿废石来源有正面和上面2个面。由图6可知：当步距为5 m时，可以看出上部废石距离出矿口还有一段距离，在本步距很多矿石未放出时，正面废石率先混入导致贫化，矿石回收率较低；当步距为6 m时，正面废石和上部废石基本同时到达出矿口；当步距为 7 m时，上部废石到达出矿口时，正面废石仍未到达，导致正面残留较多，导致回收率低；整个放矿过程靠壁残留体较少。

本次数值模拟实验中矿石回收效果与相似材料实验结果基本一致，即以回贫差作为判断指标，无贫化、低贫化和截止品位3种放矿方式对应的回贫差分别在放矿步距为6，5和5 m时达到最大，且采用低贫化放矿方式的回贫差均高于截止品位放矿方式的回贫差。因此，在条件允许的情况下，当分段高度×进路间距为18 m×20 m时，建议优先考虑低贫化或无贫化放矿方式，放矿步距为5 m或6 m左右。

图6 端部出矿数值模拟过程Fig. 6 Numerical simulation of recycling process of face-end

3 讨论

在实际生产过程中，品位低于一定值的矿石及围岩都被定义为废石，也就是说废石中会含有一定量的铁矿石。达到终止出矿条件时实际生产过程中的废石混入量要比室内相似材料模拟试验的大，但由于混入的废石中除了含有品位为0的岩石之外，还含有一定的铁矿石，所以，2种试验结果并无太大差别，张志贵等[11]的研究也证明了这一观点。

崩矿步距为回采爆破过程每次崩落的矿石层厚度，放矿步距是爆破之后松散的矿岩厚度。限于室内相似模拟实验无法模拟爆破，装填的矿石废石均为松散的颗粒，所以，实验得到的步距均为放矿步距。张成舜等[20]的研究表明：存在1个步距系数K，能够反映实验室模拟实验与实际工业实验之间的关系。K为放矿步距与崩矿步距的比值，其范围为1.00～2.00，梅山铁矿步距系数则为1.32左右。本文室内试验结果表明3种放矿方式下的最优放矿步距分别为：无贫化的为6 m，低贫化和截止品位的为5 m，所以其对应的最优崩矿步距应分别为4.5，3.8和3.8 m。

无贫化放矿形成的矿石残留体，因具有“前面留、后面收”的特点而可以得到充分回收，使崩落矿石残留体的形态最大限度地与放出体形态保持一致，从而使放矿取得良好的回收效果；图7所示为无贫化和截止品位放矿对比。由图7可知：采用无贫化放矿方式回采的过程中(图7(a)～(b))，矿岩接触较采用截止品位的(图7(c)～(d))要少很多，有明显的废石隔离层，减少了矿岩混杂的机会。脊部残留在后一分段(图 7(b))可以很好地回收。截止品位一般都比较低，截止放矿时的岩石混入率通常在50%左右[11]。采用截止品位放矿，每个步距、每个分段都要放出大量的废石，废石移动漏斗都会产生破裂并发展到极限，这样不仅增加了矿岩接触面的面积，而且明显增加了矿岩相互混杂的程度。矿岩混杂程度的增加和接触面积的增大，必然造成矿岩混杂层的体积增加并使混杂层的岩石的含量增高，从而造成更大的矿岩混杂损失。

图 7 无贫化和截止品位放矿对比Fig. 7 Comparison between cut-off grade drawing method and non-dilution drawing method

相似材料模拟实验所得3分段回收情况如表5所示。第3分段均采用截止品位方式回收。表中数据为每个分段各自的回收率，由于第2和第3分段回采时会回收上部分残留的矿石，所以该分段回收率大于100.00%。从表5可以看出：采用3种方式的最终总回收率相差不大。无贫化、低贫化、截止品位3种放矿方式在各自最优步距下的回贫差分别为 85.4%，82.6%和77.5%。因此，无贫化放矿具有“上丢下采”的特点，能最大限度地降低贫化，减少矿岩的混杂机会，取得良好的回收效果。

表5 3种放矿方式回收率Table 5 Recovery rates of three drawing modes %

但在实际生产实践过程中矿体不可能是完全的块状矿体，无贫化放矿遇到废石就停止出矿显然不合实际，而低贫化放矿简单可操作，不像截止品位放矿那样以完全以矿块为回采单元，贫化率极大。此外，低贫化放矿室内相似材料模拟实验结果也很理想，所以很适合在矿山使用。

4 结论

1) 采用不同放矿方式有不同的最优崩矿步距，无贫化放矿、低贫化放矿和截止品位3种放矿方式的最优的崩矿步距分别为4.5，3.8和3.8 m。

2) 无贫化放矿基本上不破坏矿岩界面的完整性，减少矿岩的混杂机会，能最大限度地降低贫化，在条件允许的情况下回收效果最好，但实际生践过程较难实现，且受步距影响较大。

3) 低贫化放矿回收效果较截止品位放矿效果好，在一定范围内步距对其影响较小。

4) 不同的放矿方式有不同最优放矿步距。终止出矿时步距较大则混入的废石主要来源于上部，正面残留较大；步距较小时正面废石会过早混入，整体回收率低；步距适中时正面废石和上部废石同时混入，回收效果较好。

[1] 刘兴国. 放矿理论基础[M]. 北京: 冶金工业出版社, 1995:90−116.LIU Xingguo. Theoretical base of ore flow[M]. Beijing:Metallurgical Industry Press, 1995: 90−116.

[2] 任凤玉. 随机介质放矿理论及其应用[M]. 北京: 冶金工业出版社, 1994: 114−128.REN Fengyu. The stochastic medium method of ore-drawing and its application[M]. Beijing: Metallurgical Industry Press,1994: 114−128.

[3] 程爱平, 许梦国, 刘艳章, 等. 金山店铁矿低贫化放矿试验研究[J]. 金属矿山, 2010(7): 23−25.CHENG Aiping, XU Mengguo, LIU Yanzhang, et al.Experimental study on low dilution ore drawing in Jinshadian iron mine[J]. Metal Mine, 2010(7): 23−25.

[4] 陶干强, 杨仕教, 任凤玉. 崩落矿岩散粒体流动性能试验研究[J]. 岩土力学, 2009, 30(10): 2950−2954.TAO Ganqiang, YANG Shijiao, REN Fengyu. Experimental research on granular flow characters of caved ore and rock[J].Rock and Soil Mechanics, 2009, 30(10): 2950−2954.

[5] 安龙, 徐帅, 李元辉, 等. 基于多方法联合的崩落法崩矿步距优化[J]. 岩石力学与工程学报, 2013, 32(4): 754−759.AN Long, XU Shuai, LI Yuanhui, et al. Optimization of rate of advance during ore breaking of caving method based on multi-method joint application[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(4): 754−759.

[6] 王洪江, 尹升华, 吴爱祥, 等. 崩落矿岩流动特性及影响因素实验研究[J]. 中国矿业大学学报, 2010, 39(5): 693−698.WANG Hongjiang, YIN Shenghua, WU Aixiang, et al.Experimental study of the factors affecting the ore flow mechanism during block caving[J]. Journal of China University of Mining and Technology, 2010, 39(5): 693−698.

[7] 余健. 高分段大间距无底柱分段崩落采矿贫化损失预测与结构参数优化研究[D]. 长沙: 中南大学资源与安全工程学院,2007: 58−98.YU Jian. Research on the predietion of ore dilution and loss rate and the optimization of structural parameters of high sublevel large-space drive interval pillar1ess sublevel caving[D].Changsha: Central South University. School of Resources and Safety Engineering, 2007: 58−98.

[8] 宋卫东, 何明华. 程潮铁矿采场结构参数的调整与优化研究[J]. 中国矿业, 2002, 11(4): 35−38.SONG Weidong, HE Minghua. Adjustment and optimization of mining technological data in Chengchao Iron Ore Mine[J]. China Mining, 2002, 11(4): 35−38.

[9] 程爱平. 金山店铁矿低贫化放矿试验与应用研究[D]. 武汉:武汉科技大学资源与环境工程学院, 2011: 42−47.CHENG Aiping. Experimental study and application research on low dilution ore drawing in Jinshadian Iron Mine[D]. Wuhan:Wuhan University of Science and Technology. School of Resources and Environmental Engineering, 2011: 42−47.

[10] 安龙. 梅山铁矿多端壁倾角下崩矿步距的优化研究[D]. 沈阳:东北大学资源与土木工程学院, 2011: 31−89.AN Long. The optimization study of ore breaking under different angle at Meishan iron mine[D]. Shenyang: Northeastern University. College of Resources and Civil Engineering, 2011:31−89.

[11] 张志贵, 刘兴国, 于国立. 无底柱分段崩落法无贫化放矿−无贫化放矿理论及其在矿山的实践[M]. 沈阳: 东北大学出版社,2007: 48−95.ZHANG Zhigui, LIU Xingguo, YU Guoli. Sublevel caving method of none dilution-no dilution ore theory and practice the mine[M]. Shenyang: Northeastern University Press, 2007:48−95.

[12] CHITOMBO G P. Caving mining—16 years after Laubscher’s 1994 paper ‘Cave mining-state of the art’[C]// Proceedings of the 2nd International Symposium on Block and Sublevel Caving,Perth. Australia: Australian Centre for Geomechanics, 2010:45−61.

[13] CASTRO R. Study of the mechanisms of gravity flow for block caving[D]. Brisbane: University of Queensland. Sustainable Minerals Institute, 2006: 7−34.

[14] 王培涛, 杨天鸿, 柳小波, 等. 边孔角对无底柱分段崩落法放矿影响的颗粒流数值模拟研究[J]. 金属矿山, 2010(3): 12−16.WANG Peitao, YANG Tianheng, LIU Xiaobo, et al. Particle flow numeral simulation investigation on influence of lateral opening angle on ore drawing with sublevel pillar less caving[J]. Metal Mine, 2010(3): 12−16.

[15] 仝庆亮, 严荣富. 低贫化放矿的PFC2D数值模拟[J]. 现代矿业,2014(3): 1−3.TONG Qingliang, YAN Rongfu, Numerical simulation research on the low dilution ore drawing based on PFC2D[J], Modern Mining, 2014(3): 1−3.

[16] 朱焕春. PFC及其在矿山崩落开采研究中的应用[J]. 岩石力学与工程学报, 2006, 25(9): 1927−1931.ZHU Huanchun. PFC and application case of caving study[J].Chinese Journal of Rock Mechanics and Engineering, 2006,25(9): 1927−1931.

[17] 陆玉根, 章林, 孙国权, 等. 高变分段低贫化放矿及其参数优化试验研究[J]. 金属矿山, 2014(4): 12−16.LU Yugen, ZHANG Lin, SUN Guoquan, et al. Experimental study on low dilution drawing of high and variable sublevel and its parameter optimization[J], Modern Mining, 2014(4): 12−16.

[18] 孙浩, 金爱兵, 高永涛, 等. 崩落法采矿中放出体流动特性的影响因素[J]. 工程科学学报, 2015, 37(9): 1111−1117.SUN Hao, JIN Aibing, GAO Yongtao, et al. Influencing factors on the flow characteristics of an isolated extraction zone in caving mining[J]. Chinese Journal of Engineering, 2015, 37(9):1111−1117.

[19] 孙浩, 金爱兵, 高永涛, 等. 复杂边界条件下崩落矿岩流动特性[J]. 中南大学学报(自然科学版), 2015, 46(10): 3782−3788.SUN Hao, JIN Aibing, GAO Yongtao, et al. Flow characteristics of caved ore and rock under complex boundary conditions[J].Journal of Central South University (Science and Technology),2015, 46(10): 3782−3788.

[20] 张成舜, 鞠玉忠. 关于无底柱分段崩落采矿法的放矿步距和崩矿步距[J]. 金属矿山, 1979(4): 11−13.ZHANG Chengshun, JU Yuzhong. The drawing pace and independent advance of ore breaking of sublevel caving method[J]. Metal Mine, 1979(4): 11−13.

Study of best caving steps under different ore methods of sublevel caving

JIN Aibing, SUN Hao, MENG Xinqiu, GAO Yongtao, WU Qiong, ZHANG Guang

(School of Civil and Resource Engineering, University of Science and Technology Beijing, Beijing 100083, China)

Choosing Meishan iron mine as the subject, similar material simulation experiments were conducted with large structural parameters of 18 m×20 m. By setting up different caving steps, three caving methods, i.e., none dilution caving method, low dilution caving method and the current cutoff caving method under different caving steps, were used.Then, the details of ore recycling and rock mixing were simulated by using PFC2Dnumerical simulation software. The results show that the best caving step of these three caving methods are 4.5, 3.8 and 3.8 m, respectively. Non-dilution drawing mode essentially does not destroy the integrity of the ore mine rock interface, and reduces the opportunities for mine rock hybrid, which can minimize dilution. Different methods have different optimal caving steps. When the caving step is large, waste rocks mixed in ore come from the upper and leave more positive residual. On the contrary, when the caving step is small, waste rocks from the front firstly mix into ore, resulting in low recoveries. When the caving step is medium, waste rocks from the front and up mix into ores at the same time, resulting in good recovery.

sublevel caving; ore method; caving step distance; similar material simulation; numerical simulation

TD85

A

1672−7207(2017)11−3037−07

10.11817/j.issn.1672-7207.2017.11.026

2016−12−25；

2017−02−16

国家自然科学基金资助项目(51374032，51674015)；科技北京百名领军人才培养工程基金资助项目(Z151100000315014)(Projects(51374032, 51674015) supported by the National Natural Science Foundation of China; Project(Z151100000315014) supported by the Beijing Training Project for the Leading Talents in Science and Technology)

金爱兵，博士，教授，从事岩土工程灾害治理研究；E-mail: jinaibing@ustb.edu.cn

(编辑 伍锦花)