青冈栎次生林林木综合竞争压力指数研究

吕 勇，钱升平，吕飞舟，朱光玉

（中南林业科技大学，湖南 长沙410004）

青冈栎次生林林木综合竞争压力指数研究

吕 勇，钱升平，吕飞舟，朱光玉

（中南林业科技大学，湖南 长沙410004）

以研究青冈栎林木竞争、掌握青冈栎林分竞争结构规律、为评价林木竞争压力状况提供新方法为目的。以中南林业科技大学芦头林场青冈栎次生林为研究对象，构建青冈栎优势木冠幅模型，并采取平均离差百分数调整法对模型进行调整得到青冈栎自由树冠幅模型。分别利用样地偏移法和影响力因子判别法确定对象木和竞争木。基于单木影响圈构建单木影响体，同时结合竞争压力指数（CSI）提出综合竞争压力指数（C-CSI）概念。分析得到 CSI、 C-CSI以及简单竞争指数CI与胸径均为指数函数关系。三个竞争指数均表明林木胸径越大其受到的竞争压力越小，但综合竞争压力指数C-CSI比CSI和CI有更高的相关性，说明竞争指数考虑树高的必要性，用C-CSI评价林木在林分中受到的竞争压力要优于CSI和CI。

青冈栎次生林；林木竞争；冠幅模型；综合竞争压力指数

林木竞争是指林木个体间的相互作用。干扰和竞争不仅影响着林木个体的形态、生长、发育，也影响着森林群落的结构及种群演替动态；竞争的产生主要是由于树木共享资源的有限性，研究林木竞争对于揭示林木生态适应机理、掌握林分结构规律和森林演替动态以及森林可持续经营有着重要意义。

林木竞争状况多采用林木竞争指数来反映，竞争指数是指用定量的方式描述林木之间的竞争，它在形式上反映的是林木个体生长与生存空间的关系，实质是反映树木对环境资源需求及其争取环境资源所承受的竞争压力[1]。基于不同的目的和条件，前人创立了很多的林木竞争评价指标，例如，视角竞争指数[2]、以胸高断面积为基础的竞争指数[3]、基于自由树冠幅重叠面积和林木间距的竞争压力指数[4]、基于直径和距离的Hegyi竞争指数[5]、树冠体积竞争指数[6]、以相对直径为指标的竞争指数[7-9]、包含冠幅和冠长的林木竞争指数[10]、基于交角的竞争指数[11]、基于加权Voronoi图的林木竞争指数[12]等等。它们大致可分为完备型指标和非完备型指标两大类[13]，或者分为与距离有关的单木竞争指标和与距离无关的单木竞争指标[14]。竞争指标虽然多，但是少有同时基于自由树冠幅、树高和树木间距离三个因子从三维空间考虑林木竞争的指标，本研究基于这三个因子提出了综合竞争压力指数来描述林木之间的竞争状况。

1 材料与方法

1.1 研究区概况

中南林业科技大学芦头林场位于湖南省岳阳市平江县东南部，连云山东面，地理坐标 为 113°51′52″～ 113°58′24″E，28°31′17″～28°38′00″N。境内地貌类型以中山、低山为主，但山势都较陡，海拔为124～1 273 m，林场处于湿润的大陆性季风气候区，属中亚热带向北亚热带过渡气候带，温暖湿润，日照充足，降水充沛，四季分明，年平均降水量为1 624.8 mm，年平均气温16.8℃。森林植被在全国植被区划中属亚热带常绿阔叶林区，天然植被繁茂，树种结构及林分层复杂，阔叶林主要有青冈栎Cyclobalanopsis glauca、 苦 槠Castanopsis sclerophyllus、 甜 槠Castanopsis eyrei、 木 荷Schima superba、 梧 桐Firmiana simplex、麻栎Quercus acutissima等。

1.2 材料来源

在芦头林场设置了8块青冈栎次生林标准地，标准地大小均为20 m×20 m，采用每木检尺的调查方式，调查每株树木的胸径、树高、冠幅、和坐标等基本因子，同时调查了样地的林分平均高、平均胸径、海拔、坡度、坡向、树种等因子，并利用优势木对比法选出生长状况较好的青冈栎优势木，标准地基本信息如表1所示。其中乔木总数为443株，青冈栎有378株，占85.3%，其它树种有茅栗、苦槠、甜槠等共65株，占14.7%，选择的青冈栎优势木共89株。

1.3 研究方法

1.3.1 自由树冠幅模型构建方法

构建自由树冠幅模型首先要选择优势木，利用优势木对比法，以候选优势木为中心，在立地条件相对一致的10 m半径范围内，选取出仅次于候选优势木的3～5株优势木，实测并计算其平均高、胸径与材积，如果候选优势木生长指标超过测量的规定指标，即可入选。基于青冈栎次生林中的优势木数据，利用SPSS软件对优势木的胸径与冠幅进行相关性分析，并采用线性回归分析法，构建青冈栎优势木冠幅模型。采用标准表编制时的平均离差百分数调整法对模型进行调整，得到青冈栎自由树冠幅模型。

表1 青冈栎次生林样地概况Table 1 Sampling plots overview of Cyclobalanopsis glauca secondary forests

1.3.2 对象木与竞争木的确定

单木竞争指标的计算首先就是要确定竞争木，竞争木的确定主要考虑的问题就是边缘效应，对于位于样地边缘的树木，其竞争木可能位于样地外，所以竞争指数的计算时可能导致其数值有偏差。消除边缘效应的方法有多种，如镜像和偏移法，这两种方法原理相同，即设想样地周围的情况与样地一致，样地内的林木全可以作为对象木，这两种方法可以减小边缘木竞争指数计算的偏差；此外还有距离缓冲法，即将样地边缘向样地内以一定距离进行平移，建立缓冲区，该区内的树木只选作竞争木，此法会减少研究的样本数量，考虑到本研究样地面积较小，为保证样本数量，采用平移法消除边缘效应。

本研究采用的竞争压力指数涉及到了自由树冠幅重叠面积，故采用树冠重叠法确定竞争木，即当邻近木自由树冠幅与对象木自由树冠幅面积有重叠就可选作该对象木的竞争木，这里采用影响力因子[15]进行判定，公式如下：

式（1）中：Iij为第i株树与第j株树的影响力因子，Lij为第i株树与第j株树之间的距离（m），Ri为第i株树的自由树冠幅半径（m），Rj为第j株树的自由树冠幅半径（m）。当Iij＞0时，两株树存在冠幅重叠，否者不重叠。

1.3.3 单木影响体构建

影响圈[14]（见图1）是指林木潜在生长得以充分发挥时所需要的最大生长空间，常以自由树的树冠面积表示。但是树木生长所需要的空间并不只表现在平面上，应该是一个立体的生长空间。因此，基于树木的影响圈，结合树高，拓展形成圆柱体，将这个三维圆柱体空间定义为该树木的影响体（见图2），以此来表示林木潜在生长得以充分发挥时所需要的三维生长空间，这样更能反映树木的生长需求。

对于对象木3，假设其存在两株竞争木1和2，则其影响圈示意图如图1所示，影响体示意图如图2所示。

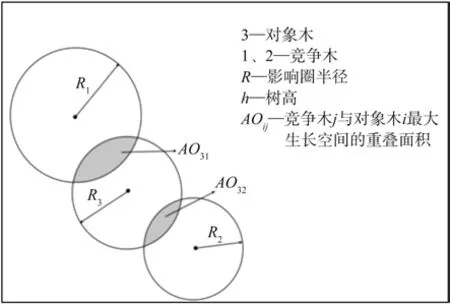
图1 林木影响圈示意Fig.1 Diagram of circle of influence

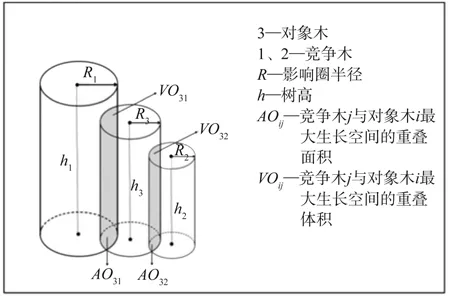
图2 林木影响体示意Fig.2 Diagram of cylinder of influence

2 结果与分析

2.1 青冈栎自由树冠幅模型构建

树冠是树木主要测树因子之一，是树木进行光合作用的重要场所，树冠大小在很大程度上可以反映林木在竞争生长中所处的地位，而冠幅是反映树冠大小的重要特征因子。自由树是指其周围没有竞争木与其争夺生长空间，可以充分生长的林木[15]。在现实中，要寻找数量相当的自由树是难以实现的，而优势木的生长最接近于自由树，故本文以优势木数据为对象，利用优势木胸径与冠幅的关系，建立冠幅模型。

对8块标准地中的89株青冈栎次生林优势木按胸径大小进行排序，编号从第1号到第89号。利用SPSS对优势木的胸径、冠幅（以东西和南北冠幅的平均值表示）作散点图并进行相关性分析，分析结果见表2和图3，从图中可以看出其树木胸径与冠幅之间呈线性相关。并拟合得到芦头林场青冈栎次生林优势木的冠幅模型如式2。

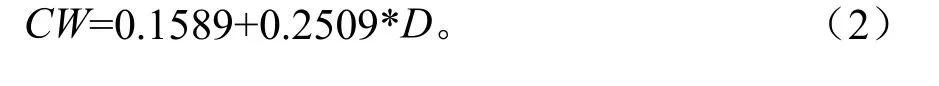
表2 模型汇总和参数估计†Table 2 The model and parameter estimation

图3 胸径与冠幅散点Fig.3 The scatter diagram of DBH and canopy

虽然优势木的生长与林分中自由树的生长接近，但利用优势木所建立的模型表现的是优势木生长的平均水平，与自由树的生长还是有一定的差距，所建立出的青冈栎冠幅模型还不能达到自由树冠幅模型的要求。本研究中为解决这问题，采用标准表编制时所用的系数平均离差百分数调整法，将青冈栎优势木冠幅模型系数进行提升。从89株优势木中选取出模型线以上的优势木7号、21号、73号、84号这4株青冈栎优势木作为进行系数调整的数据，建立出系数调整模型，模型如下：

式（3）、（4）中：q为冠幅相对误差值，CWi为林木自由树冠幅，CWj为林木实际冠幅（m），Q为整体调整系数。

4株优势木概况及调整系数详见表3。

表3 调整系数计算Table 3 Adjustment coefficient calculation

利用调整系数模型，计算得出这4株优势木的冠幅相对误差值分别为0.132 6、0.099 0、0.053 0、0.130 3，Q=1.115 7。将原系数乘以Q后得到调整后的青冈栎次生林林木自由树冠幅模型为：

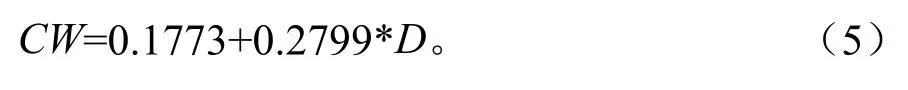
2.2 综合竞争压力指数

2.2.1 林木综合竞争压力指数的提出

林木竞争是普遍存在的，评价林木的竞争状况通常采用林木竞争指标，林木竞争指标的种类很多，根据其涉及的林木基本因子可以将其归为3类，仅仅考虑对象木和竞争木的水平方向上的大小或垂直方向上的大小，如直径、胸高断面积、冠幅、树高，所构建的林木竞争指标，称之为一维林木竞争指标；考虑对象木和竞争木的水平方向上的大小或垂直方向的大小和两者之间的距离所构建的林木竞争指标，称之为二维林木竞争指标；综合考虑对象木和竞争木在水平方向的大小和垂直方向的大小以及对象木和竞争木之间的距离所构建的林木竞争指标，称之为三维林木竞争指标。三维及以上的林木竞争指标就可称之为林木综合竞争指标。

林分中任意单木，都有自身的影响圈和影响体。根据对象木和竞争木的影响圈重叠部分的面积大小构建的林木竞争压力指数[4]可用来表达林木间竞争强烈程度，但林木竞争压力指数只考虑对象木和竞争木在水平方向上的分布，没有考虑对象木和竞争木在垂直方向上的分布，所以，综合考虑对象木和竞争木在水平方向和垂直方向上的分布，根据对象木和竞争木的影响体重叠部分的体积大小构建的林木竞争指标则能更全面地表达林木间竞争强烈程度。

因此，基于自由树的影响体和Arney提出的林木竞争压力指数CSI（Competition Stress Index），提出了林木综合竞争压力指数（Comprehensive-CSI）用来全面表达对象木和竞争木之间的干扰程度，并构建其计量模型。

对于林分任意对象木i，其竞争压力指数CSI计量模型如式6。

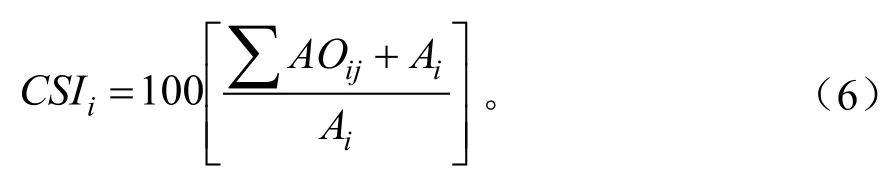
式中：CSIi为对象木i的竞争压力指数；AOij为竞争木j与对象木i最大生长空间的重叠面积（如图1）；Ai为对象木i的影响圈面积。

而其林木竞争压力综合指数C-CSI计量模型如式7。

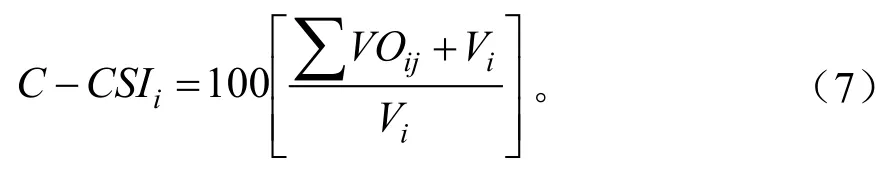
式中：C-CSIi为对象木i的综合竞争压力指数；VOij为竞争木j与对象木i最大生长空间的重叠体积（如图2）；Vi为对象木i的影响体体积。

2.2.2 单木C-CSI案例分析

在第Ⅰ号样地中随机选择出第5号样木，其树高为12.3，胸径为14.0 cm。利用构建的青冈栎自由树冠幅模型CW=0.177 3+0.279 9*D，求出该树的自由树冠幅为4.095 3 m，结合林分调查的树木坐标数据和其它青冈栎林木的自由树冠幅大小以及树木之间的距离，利用影响力因子判别法可判断该青冈栎林木有11株竞争木，再利用相关的数学方法计算对象木与竞争木的自由树重叠面积和重叠体积详见表4。

则利用相应的CSI计算模型（式6），可求得其CSI为342，利用相应的C-CSI计算模型（式7）可求得其C-CSI为314。

2.3 竞争指数与胸径的关系

林木之间的竞争会影响林木的生长发育，对林木胸径、树高、冠幅等都有一定的影响，但是林木的胸径、树高等生长因子也在一定程度上反映了林木在林分受到的竞争压力状况。由于外业调查时胸径的测量精度大于树高[16]，故采用Ⅰ-Ⅷ号8个样地378株青冈栎的CSI及C-CSI值分别分析它们与胸径因子的关系，样地CSI及C-CSI概况见表5。1974年Hegyi提出了简单竞争指标CI，该指标操作简便，运用广泛，本文同时分析了以四邻体计算的简单竞争指数CI与胸径的关系，并进行比较，详见图4。

表4 第5号样木竞争木信息Table 4 Competition tree information of No. 5 tree

表5 8个样地竞争指数均值Table 5 Average of competition index of 8 sample plot

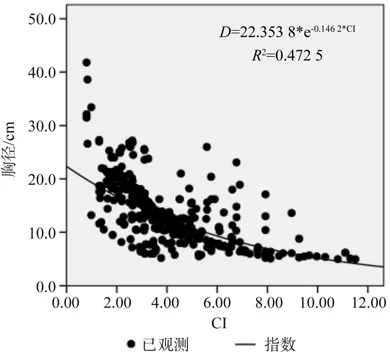
图4 竞争指数与胸径相关图Fig.4 Competition index and DBH related diagrams

从表中可以看出，8个样地的CSI和C-CSI都不算大，表明芦头林场青冈栎竞争压力不大，竞争状况良好；从图中可以看出CI、CSI、C-CSI三个竞争指数具有一致的趋势，均表明胸径越大，竞争指数越小；C-CSI的拟合度比CSI好，说明在评价林木竞争状况时考虑树高的必要性；C-CSI比CSI和CI的相关性更高，说明C-CSI更能表达竞争指数与胸径的关系，更加能表达林木受到的竞争压力状况。

3 结论与讨论

（1）通过分析芦头林场青冈栎次生林优势木数据，得出其胸径与冠幅呈显著线性相关，从而构建了青冈栎优势木冠幅模型为CW=0.159+0.251*D，自由树冠幅模型为CW=0.1773+0.2799*D。

（2）基于自由树的影响圈，结合自由树的树高，拓展形成圆柱体，构建了单木影响体，从三维空间分析林木的生长空间。

（3）基于影响体，结合竞争压力指数，提出了综合竞争压力指数C-CSI，从三维空间研究林木竞争，并构建了综合竞争压力指数的计量模型为：

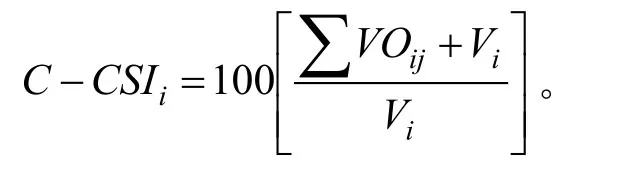
（4）以1号样地的5号样木为研究对象进行综合竞争压力指数的案例分析，得出其竞争木有11株，经计算其CSI为342，C-CSI为314。

（5）芦头林场青冈栎竞争压力不大，竞争状况良好；林木胸径越大其受到的竞争压力越小，综合竞争压力指数C-CSI比CSI和CI有更高的相关性，C-CSI更能表达林木在林分中受到的竞争压力状况。

研究在CSI的基础上结合树高提出了C-CSI，同时考虑了林木之间距离以及林木在水平和垂直方向上的分布，从三维空间分析林木之间的竞争关系，相比以前的竞争指数，该指数更加全面。该指数的计算涉及树高，虽然目前树高的测量可以达到很精确的水准，但在以后的研究中如果可以利树高曲线模型获取树高该指数将有很大的应用前景。

[1]汤孟平.森林空间结构分析[M].北京:科学出版社,2003.

[2]Newham R M. The development of a stand model for Douglasfir[J].PhD thesis.Forestry University B C,1964,21(5):37-42.

[3]Opie J E. Predictabilility of individual tree growth using various definitions of competing basal area[J]. Forest Science, 1968,14(3): 314 -323.

[4]Arney J D.Tables for quantifying competitive stress on individual trees[J]. Pacific forest research centre, 1973, 15(3): 511-518.

[5]Hegyi F. A simulation model for managing jack-pine stands Fries[J]. Growth models for tree and stand simulation.Stockholm: Royal College of Forestry, 1974, 74-90.

[6] Biging GS, Dobbertin MA.Comparison of diameter-dependent competition measures for height and basal area growth of individual conifer trees[J]. Forest Science,1992,38(3):659-720.

[7]孟宪宇,张 弘.闽北杉木人工林单木模型[J].北京林业大学学报,1996,18(2):1-8.

[8]马友平,马友金,马家龙.日本落叶松人工林单木模型的研究[J].湖北民族学院学报,2000,20(2):15-17.

[9]姚东和,吕 勇.基于人工神经网络的杉木竞争生长模型研究[J].中南林学院学报,2001,21(1):17-20.

[10] 陈东来,刘丽华,张景兰.林分密度的新指标一冠积指数[J].东北林业大学学报,2003,31(5):15-17.

[11] 惠刚盈,胡艳波,赵中华, 等.基于交角的林木竞争指数[J].林业科学,2003,49(6):68-73.

[12] 李际平,房晓娜,封 尧, 等.基于加权Voronoi图的林木竞争指数[J].北京林业大学学报,2005, 37(3):61-68.

[13] 关玉秀,张守攻.竞争指标的分类与评价[J].北京林业大学学报,1992, 14(4):1-7.

[14] 孟宪宇.测树学[M].北京:中国林业出版社,2012.

[15] 吕飞舟,吕 勇,等.蒙古栎次生林林木竞争压力指数研究[J].林业资源管理,2015(2): 71-76.

[16] 欧阳君祥.天然次生林择伐木的控制技术[J].中南林业科技大学学报,2015,35(8):32-35.

[本文编校：吴 彬]

Study on comprehensive competition stress index ofCyclobalanopsis glaucasecondary forest

LV Yong, QIAN Shengping, LV Feizhou, ZHU Guangyu
(Central South University of Forestry & Technology, Changsha 410004, Hunan, China)

The aim of this study is to learn the trees competition and the competition structure law of forest stand ofCyclobalanopsis glauca, provide a new method forevaluating trees competition. This study used theCyclobalanopsis glaucasecondary forest of LuTou tree farm as the research object，builtthe open-growing tree canopy model ofCyclobalanopsis glaucafrom dominant trees canopy model by referencing the method of average deviationpercentageadjustment. Determined the object trees by sample area migration method and determined the competitive trees by the influential factor decision method. Built Cylinder of influencebase on the Circle of influence, came up with the comprehensive-competition stress index. The relation between CSI、C-CSI、CI and DBH were exponential function. The three competition indexes showed that the bigger the DBH was, the smaller the value of competition index was, C-CSI got highercorrelation than CSI and CI, it showed the necessity for competition indextaking into account the height of tree, and the C-CSI was better than CSI and CI when evaluating the trees competition.

Cyclobalanopsis glaucasecondary forest; trees competition; crown model; comprehensivecompetition stress index

S792.18；S718.54 文献标志码：A 文章编号：1673-923X(2017)10-0001-06

10.14067/j.cnki.1673-923x.2017.10.001

http: //qks.csuft.edu.cn

2016-06-07

林业公益性行业科研专项（201504301）；国家自然科学基金项目（31570631）；湖南省研究生科研基金创新项目（CX2015B293）；中南林业科技大学研究生创新基金项目（CX2015B13）

吕 勇，教授，博导；E-mail：727065572@qq.com

吕 勇，钱升平，吕飞舟，等. 青冈栎次生林林木综合竞争压力指数研究[J].中南林业科技大学学报，2017, 37(10): 1-6.