系泊系统的优化设计

陈桂糖++任驰远++邓秋福++余莎++黄辉红++蒲思蓓

DOI：10.16661/j.cnki.1672-3791.2017.30.040

摘 要：对于系泊系统的设计问题，以悬链线方程为基础，通过静力平衡和刚体力矩平衡理论确定系泊系统中各个参数之间的联系，推导出系泊系统整体的数学模型。再利用牛顿-拉夫逊迭代对其进行求解，最终得到不同海况下钢桶和各节钢管的倾角、浮标的吃水深度及游动区域、锚链的形状及约束条件下的重物球的质量等结果，并给出最优系泊系统设计的方案。

关键词：系泊系统 悬链线 静力平衡 钢体力矩平衡 牛顿-拉夫逊迭代

中图分类号：P75 文献标识码：A 文章编号：1672-3791（2017）10（c）-0040-04

系泊系统是近浅海观测网的重要组成部分，如何设计最优的系泊系统从而促进信号的传播具有重要意义。针对系泊系统设计问题，基于2016年全国大学生数学建模竞赛A题所提供的近浅海观测网传输接点的相关数据，首先运用悬链线方程推导出锚链的数学模型，再根据静力平衡和力矩平衡理论建立其余各部件的平衡状态方程，通过Newton-Raphson迭代对其进行求解，最终得到系泊系统整体的数学模型。在模型的基础上，给出具体的设计结果，即确定锚链的型号、长度和重物球的质量，使得系泊系统能够在风速和水速最大时以及潮汐现象导致的海水深度变化的情况下，使得浮标的吃水深度和游动区域及钢桶的倾斜角度尽可能小。

1 模型假设

（1）静力分析时，忽略波浪对系统载荷的影响。

（2）忽略锚链的弹性形变[1]。

（3）浮标所受的风力方向平行于海平面方向。

（4）在风力作用下，浮标的上表面平行于海平面，不与海平面呈一定夹角。

（5）锚泊系统各部件视为钢体，不会发生形变。

2 模型建立

2.1 結构简图

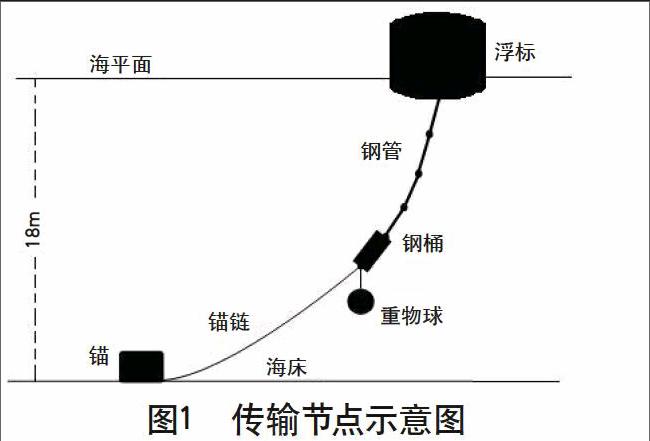
近浅海观测网的某传输节点结构简图如图1所示。

2.2 锚链的受力分析

如图2所示，锚链受到的力有自身重力WS、锚拉力T1、钢桶拉力T2。

不考虑锚链的弹性，按照静力悬链线理论可以推导出锚链的数学模型[2]：

其中，S为锚链长度；TH为锚链水平拉力；H为悬链线水平距离；Z为悬链线竖直距离；θ1为锚链末端与海床的夹角；θ2为锚链上接点切线方向与水平方向的夹角；W为单位长度质量。

2.3 钢桶的受力分析

如图3所示，钢桶受到的力有自身重力G2、重物球的重力G0、浮力B2、锚链拉力Tx1与Ty1、钢管拉力Tx2与Ty2。

钢桶处于静力平衡状态，将钢桶视为质点，根据钢桶的垂直和水平方向受力平衡可以得到：

同时，将钢桶视为钢体，它处于力矩平衡状态，因此，以钢桶上铰链接点为转轴，按照力矩平衡关系得到：

其中，钢桶的质量m2和重物球的质量m0，有钢桶重力G2=m2g，重物球重力G0=m0g；钢桶的直径d2及长度l2，有钢桶的浮力为：

2.4 钢管和浮标的受力分析

钢管和浮标的受力分析[3]与钢桶类似，在此不再赘述了。

2.5 临界条件分析

在水平风力较大时，锚链被拉紧，锚链的海底夹角为正，即θ1≥0，按照前述的悬链线模型可以求解；而当风力较小时，锚链下端沉在海底，此时不能使用标准的悬链线模型描述锚链状态。因此，需要单独对拖地形态下的锚链建立数学模型。锚链拖地状态如图4所示。

当锚链拖底时，拖底段的锚链是一条直线，不满足悬链线模型，只有锚链开始从海底升起后，才满足悬链线方程。此时，锚链与海底相切，即锚链与海底的夹角为零，即将θ1为恒值0，得到锚链的数学模型如下：

3 模型求解

3.1 问题1的求解

3.1.1 临界风速

风速较大时，锚链不会拖底，而风速较小时，锚链拖底，本文称使得锚链恰好拖底时的风速为临界风速。由于高于和低于临界风速的锚链模型不同，因此本文首先找出锚泊系统的临界风速。本文首先使用标准悬链线模型模拟不同风速下的锚链海底夹角，如图5所示。

由图5可知，当风速大于22.34m/s时，锚链的海底夹角大于0°，而当风速小于22.34m/s时，该夹角小于0°，这与海底是平面矛盾，因此，得到该锚泊系统的临界风速约为22.34m/s。

3.1.2 不同风速的结果

当风速分别为12m/s和24m/s时，钢桶和各钢管与竖直方向的倾斜角度、吃水深度、浮标游动区域如表1所示。

3.1.3 不同风速下的锚泊系统几何形态

根据MATLAB编程绘图，可以得到风速分别为12m/s和24m/s时系泊系统锚链的形状，并且可以得到浮标的具体位置，如图6所示。

3.2 问题2的求解

风速为36m/s时，重物球质量1200kg的锚泊系统状态，结果如表2所示。

由表2可知，在海面风速为36m/s，重物球的质量为1200kg条件下，钢桶的倾斜角度9.59°>5°，使得设备的工作效果较差，锚链在锚点与海床的夹角20.53°>16°，使得锚会被拖行，故我们需要不断调节重物球的质量，使得钢桶的倾斜角度不超过度，锚链在锚点与海床的夹角不超过16°。

3.2.1 重物球质量的优化

根据题设，调节重物球的质量，使得钢桶的倾角β1≤5°，且锚链在锚点与海床的夹角θ1≤16°，利用MATLAB编程得到临界重物球的质量介于2140～2150kg之间，绘制图7，故重物球的质量应满足m0≥2140kg。

本文进行重物球大概范围的查找，可以得到随着重物球质量的增加，倾斜角度随之减小，得到最小重物球质量应该在2140～2150kg之间；再对重物球的质量进行细分，使之达到最优，由图7可知，满足钢桶的倾角β1≤5°条件的最小质量为2050kg，满足锚链在锚点与海床的夹角θ1≤16°条件的最小质量为2148kg，当同时满足这两项条件的重物球质量应2148kg。

3.2.2 优化后的锚泊系统状态

优化后，当重物球的质量为2148kg时，锚泊系统各参数的值如表3所示。

且得到浮标的具体位置，如图8所示。

4 结语

在系泊系统的设计中，本文使用静力平衡、钢体力矩平衡将实际问题转化为数学模型，再利用迭代运算将抽象的问题具体化，从而给出了最优系泊系统设计的方案。

优点：问题1，2建立的是二维空间下锚泊系统的数学模型，在一定程度上简化了模型，使模型更容易实现。模型的计算采用专业数学软件，可行度高，便于推广。

缺点：在模型的建立过程中，本文把锚泊系统的各部件都视为了刚体，不发生形变，但实际上锚泊系统的各部件会发生形变。因此模型求得的结果与实际结果还是有一定差距。

参考文献

[1] 肖越.系泊系统时域非线性计算分析[D].大连理工大学船舶工程学院，2006.

[2] 杨鑫.锚泊系统的快速计算及其应用[D].大连理工大学，2015.

[3] 王磊.单点系泊系统的动力学研究[D].中国海洋大学，2012.endprint