基于分数阶小波变换的图像隐写分析

赵鸿图 刘 芳 侯守明

(河南理工大学计算机科学与技术学院 河南 焦作 454000)

基于分数阶小波变换的图像隐写分析

赵鸿图 刘 芳 侯守明

(河南理工大学计算机科学与技术学院 河南 焦作 454000)

为了提高现有的图像隐写分析算法的检测性能，提出一种基于分数阶小波变换的图像隐写分析算法。该算法首先通过二维分数阶小波变换将图像映射到分数阶小波时频域内。然后在时频域内使用主成分分析提取隐写图像高频子带的主成分特征统计量、计算主成分的信息熵、构建敏感特征向量。最后采用支持向量机(SVM)对该算法所提特征进行分类。通过仿真实验利用所提算法分别对三种隐写算法下不同嵌入率的隐写结果进行检测，结果表明该算法可有效提高隐写分析准确率。

隐写 隐写分析 分数阶小波变换 主成分分析 支持向量机

0 引 言

隐写是在不影响视觉和使用的情况下将秘密信息隐藏在公开的信息中。隐写分析是隐写的反过程，主要根据信息嵌入载体中而引起载体统计特性发生改变这一特点，检测或者提取出隐藏在载体中的秘密信息[1]。目前隐写分析根据检测的目标不同可分为专用隐写分析和通用隐写分析[2]。由于通用隐写分析具有广泛的适用性，因此成为隐写分析研究的重点和难点，本文主要讨论通用隐写方法。

传统隐写分析大都基于离散小波变换DWT(Discrete wavelet transform)实现隐写图像检测。文献[3]根据载体图像和预测误差图像的小波域高频系数的不同，利用线性回归模型检测灰度图像的秘密信息，实现LSB替换隐写分析。文献[4]利用小波域内低频子带系数和的高频子带系数相关性的统计分析，提出了基于整数提升小波变换的彩色图像隐写分析。文献[5]将图像进行小波分解得到子带，并对第一级小波对角子带进一步分解得到新的子带，提取这些子带特征用于分类。文献[6]通过载体图像及其预测误差图像进行最优小波包分解得到的子带系数，提取各子带的直方图特征函数多阶矩作用于分类，并结合遗传算法优化分类。文献[7]利用小波变换将图像分解成不同频率子频带并用最优小波包变换来分析秘密信息系数，提出了基于小波变换的通用隐写分析。

由于DWT对信号的分析仅局限于时频域，导致对随机隐写噪声的敏感度较弱，适用性较低，检测率不高。此外关于离散分数阶小波变换DFRWT(Discrete fractional wavelet transform)在隐写分析领域中的研究成果还比较少，因此本文提出了基于离散分数阶小波变换DFRWT(Discrete fractional wavelet transform)的隐写分析检测算法。该算法将小波变换的多分辨分析优点和分数Fourier变换FRFT(fractional Fourier transform)的分数域表征功能相结合，使本文的图像隐写分析算法在时间-分数阶域具有表征信号特征的能力。相较与传统的DWT，增加了可选阶次，可灵活地调节小波系数，对隐写噪声信息更加敏感。

1 分数阶小波变换

1.1 FRWT定义

Mendlovic与Huang分别于1997年和1998年先后提出了FRFT[8]和分数阶小波包变换[9]，以上两种定义是将信号进行分数阶Fourier变换(FRFT)映射到分数阶域内，再进行小波变换WT(wavelet transform)，但其结果不具备时-分数域局部化特征。Shi等[11]从时频分析角度分析了FRWT的基本性质，提出具有时-分数阶域局部变化新型FRWT。

通过一族分析宽度不断变化的基函数ψp;a,b(t)对信号f(t)进行分数阶卷积分析，得到p阶FRWT表达式[11]：

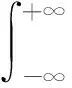
(1)

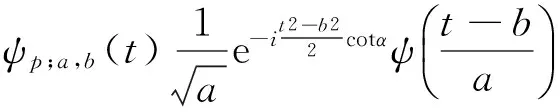
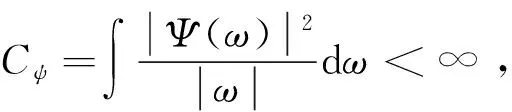
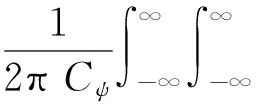
(2)

1.2 二维DFRWT分析

二维FRWT是在一维连续FRWT表达式的基础上进行扩展，则二维连续FRWT为：

Wp1,p2;x,y(a,b1,b2)=

(3)

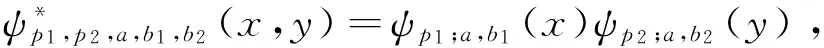
其中:α1=p1π/2,α2=p2π/2为分数阶Fourier域与时域夹角，p1,p2为二维FRWT的阶次，a、b1、b2分别是尺度因子和时移因子。当p1=p2=1,α1=α2=π/2时，Wp1,p2;x,y(α1,α2;b1,b2)将变成二维WT。

2 DFRWT 系数分解与重构

2.1 DFRWT系数分解

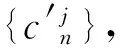
(4)

同理可得：

(5)

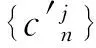
2.2 FDFRWT系数重构

〈fj+1(t),φp,j,k(t)〉+〈Dj+1(t),ψp,j,k(t)〉=

(6)

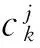
(7)

其中，

g0(k)=〈φj+1,0(t),φj,k〉=h0(N-1-k)

g1(k)=〈ψj+1,0(t),φj,k〉=(-1)k+1h0(k)

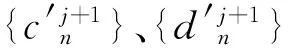
二维的DFRWT分解与重构是对一维DFRWT进行二维扩展，而二维图像分解为分数域低频、水平分数域高频、垂直分数域高频、对角分数域高频子带形式。

3 PCA

主成分分析PCA,又称K-L变换，是寻求有效的线性变换的经典方法之一[13]。主要研究如何通过少数主成分来解释多变量的方差，并尽可能地保留原始数据的大部分信息，且彼此之间互不相关，从而达到对特征空间降维的目的。

该特性常用于信号特征的提取。设x=[x1,x2,…,xn]T为n维列向量，A为n维列向量组成正交矩阵。AT=A-1,AAT=I,I为单位矩阵。Y在A上的投影为Y+AX，Y中的元素相互独立且不相关。若X已被标准量化处理，则Y的协方差为：

Cy=Cov(YYT)=E(YYT)=

E(ATXXTA)=E(ATRA)=Λ

(8)

其中:R为X的自相关矩阵，

4 基于DFRWT的隐写分析算法

4.1 算法分析

隐写是在不影响视觉感官的情况下把秘密信息潜入到图像中。在信号处理时，一般把秘密信息作为可用随机过程来描述的随机噪声。设秘密信息为高斯白噪声，其均值为0，方差为σ2。则加性噪声隐写模型：

x=s+αw

(9)

其中:x为加密信号，s为载体信号，w为秘密信号，α为嵌入系数，s和w相互独立，且E(w)=0。

依据DFRWT线性变换的叠加性可知[14]，x经过DFRWT后等于载体信号s和噪声信号w各自经过DFRWT的叠加，因此将两边同时做DFRWT可得：

Xp=Sp+αWp

(10)

其中：Xp、Sp和Wp分别表示离散信号x、s和w的离散DFRWT，p表示FRWT的阶数。

隐写后的图像经过DWT变换后，隐写噪声主要集中在高频子带中，而传统的DWT对随机噪声的敏感度不理想。利用DFRWT对图像进行多尺度分解后，低频分量和高频分量随p值变化而变化。p值在1附近时，高频分量仍能保持稀疏性，但不再集中在少数系数上，所占比例增大，而低频分量有所降低。即在一定的范围内，p值的下降对低频分量能量和高频分量能量有反向变化影响。将Lena图像嵌入隐写信息，分别采用DFRWT和DWT对隐写后的Lena图像进行分析比较，如图1、图2所示。

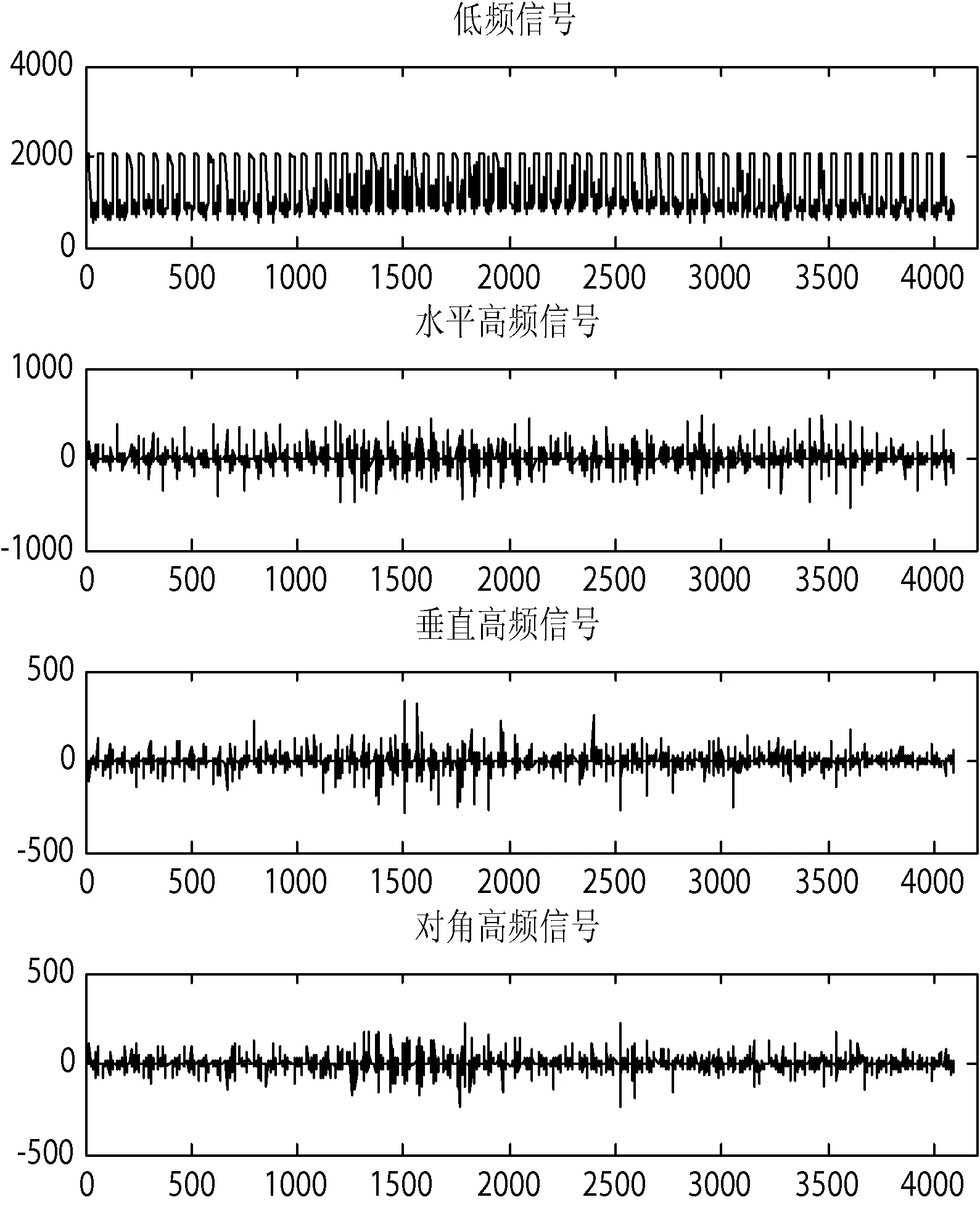
图1 WT分解提取低、高频信号结构图

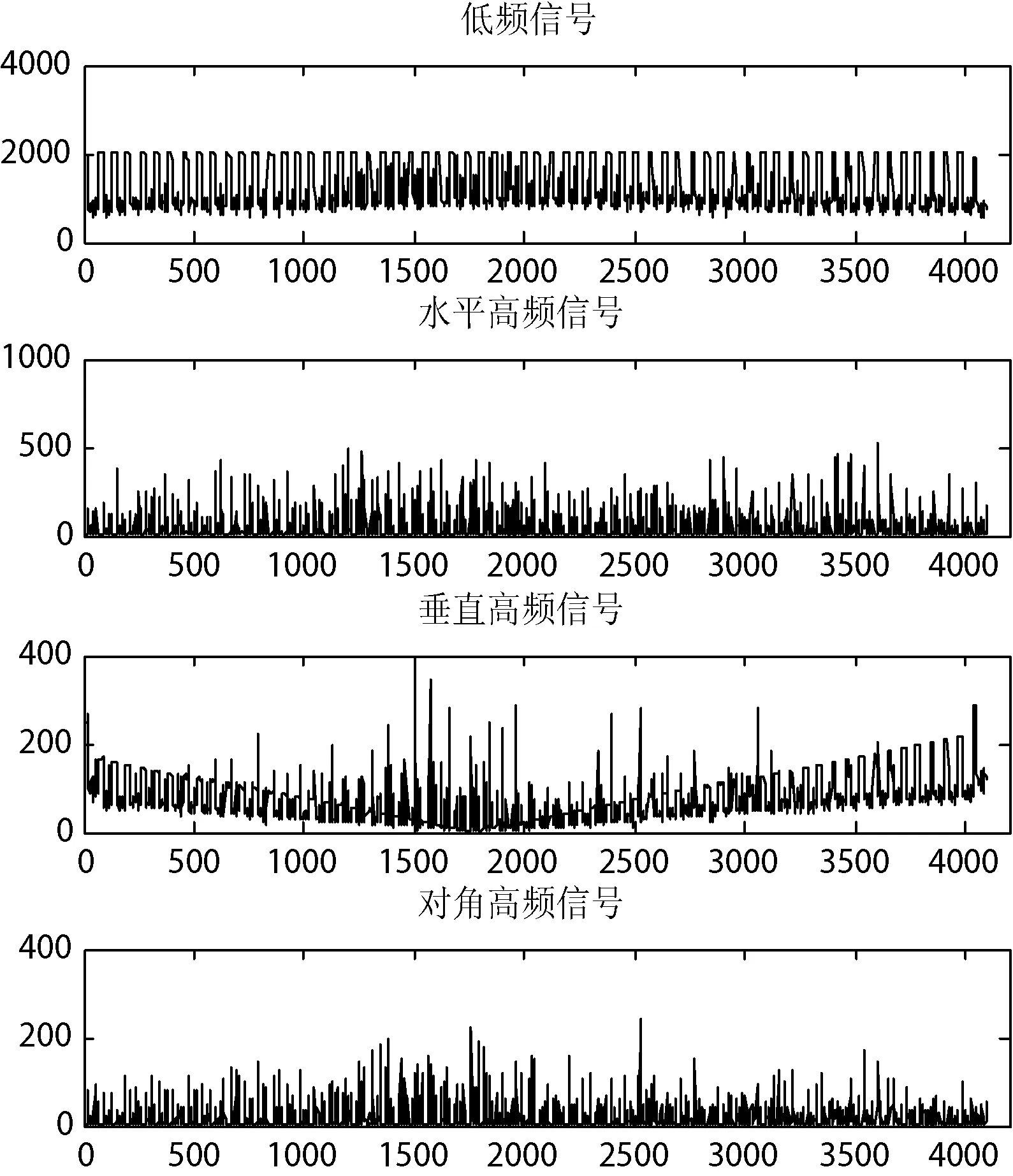
图2 DFRWT分解提取低、高频信号结构图

图1是图像经过DWT分解后的低频子带及水平、垂直、对角高频子带分解系数。图2是图像经过DFRWT(p1=p2=0.9)分解后的分数域低频子带及水平、垂直、对角线3个方向的分数域高频子带分解系数。从图1和图2对比可得，隐写后的图像经过DFRWT提取高频子带信息和传统的DWT提取高频子带信息相比较，DFRWT对高频信息更加敏感，提取的信息更加丰富。

按照PCA原理，由式(8)得Y的协方差：

Cy=Cov(XXT)=E(XXT)+

E((a(Sp+αWp))(a(Sp+αWp))T)=

(11)

其中，定义对角矩阵Λs={λs11,λs22,…,λsnn}，Λw={λw11,λw22,…,λwnn} ，则对角矩阵Λ={α2(λs11+λw11),α2(λs22+λw22),…,α2(λs33+λw33)}。

由式(11)可得，载体图像嵌入秘密信息改变了载体图像中主成分特征值。因此，可以提取并分析图像隐写前后的主成分特征值，并将主特征值的信息熵作为检测秘密信息是否存在的评价指标。

4.2 算法流程

图像隐写分析可分为以下三步骤：

(1) 提取高频系数

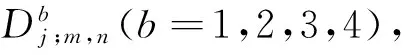
(2) 构建敏感特征向量Vfeatures

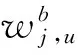
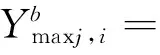
(12)

(13)

(14)

(15)

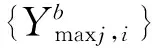
根据式(14)和式(15)分别计算主元特征的方差和信息熵，将其作为隐写图像的敏感特征，并构建敏感特征向量。

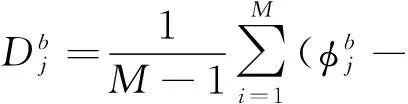
(16)

(17)

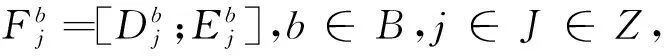
(3) 特征向量Vfeatures分类

利用SVM对基于DFRWT算法提取的向量特征Vfeatures进行分类。其中SVM内积函数采用核函数RBF，RBF核支持向量机的分类性能由可调节参数 (惩罚参数c和核函数参数g)决定。因此，本文采用交叉验证CV(Cross Validation)的方法求解最优参数c和g[14]。

5 实验仿真

从标准图像库BOSSbase[15]中随机选取1 000张大小为512×512的图片作为实验样本，实验平台为Matlab 7.0。本算法针对LSB替换算法、LSB匹配算法以及nsf5算法的隐写结果分类检测，和经典spam隐写分析算法进行比较[16]。分别在三种隐写算法下对实验样本嵌入0.1、0.25、0.5、0.75、1 bpp秘密信息，生成相应的隐秘图片库用于实验。对于每次随机选出的1 000张图片隐写前后形成的2 000张图片分为训练样本和验证样本。实验结果如表1-表3所示。

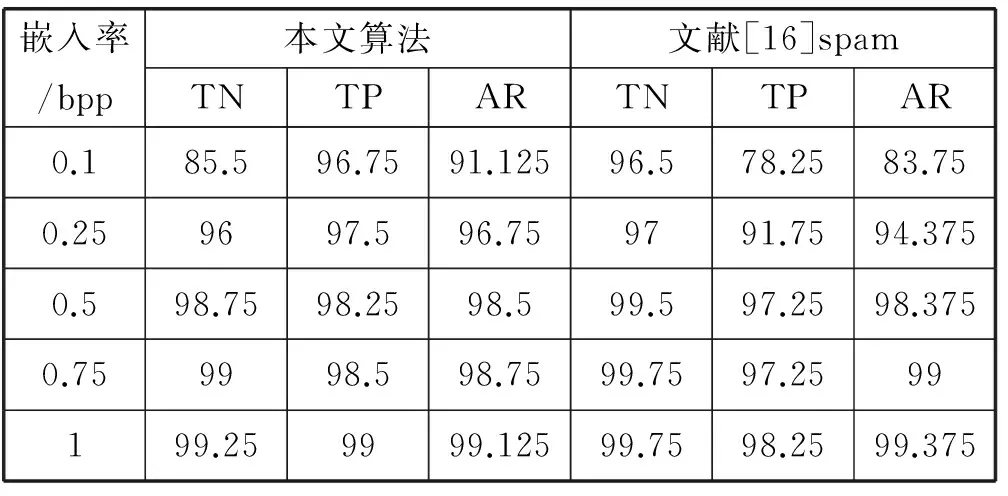
表1 检测LSB替换的实验数据表(p=0.8)

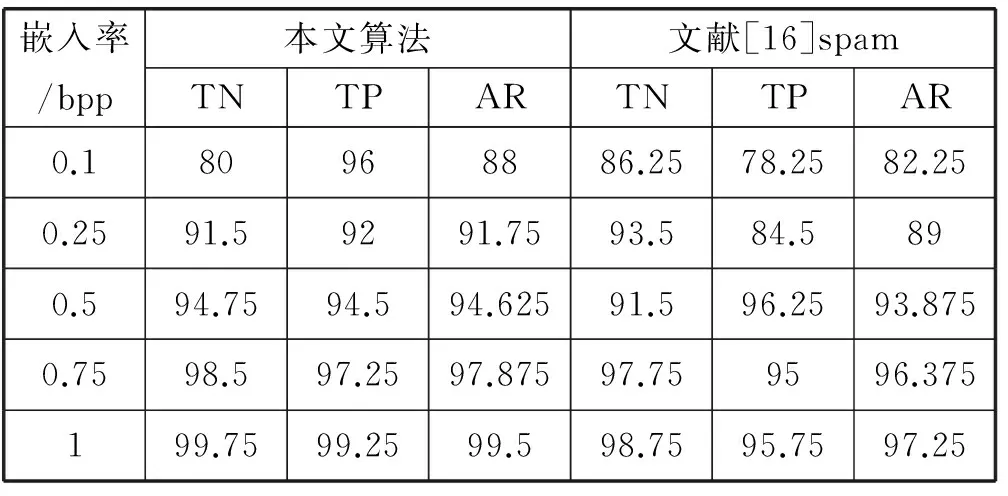
表2 检测LSB matching的实验数据表(p=0.8)

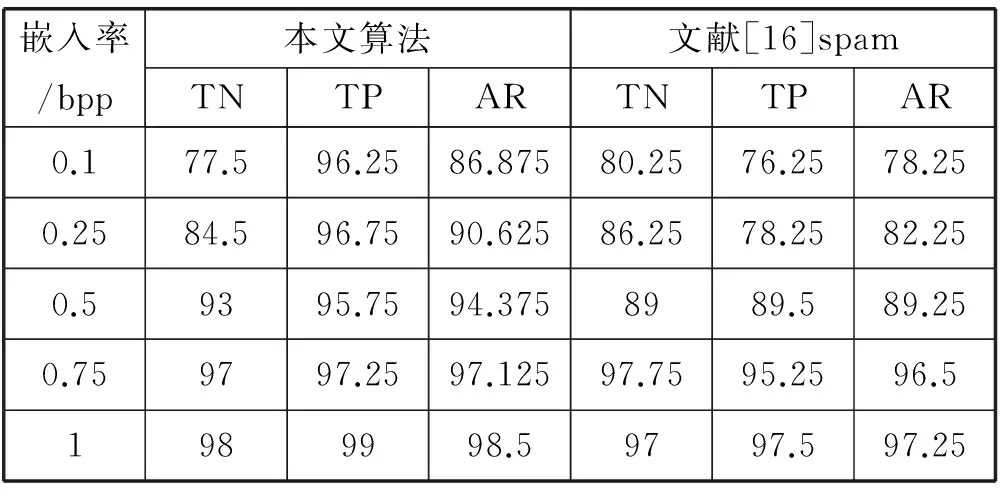
表3 检测nsf5的实验数据表(p=0.9)

表中TN为真阴率，即载体图像检测为载体图像的概率，TP为真阳率，表示加密图像检测为加密图像的概率，AR是平均正确率。实验对比分析表明，最优阶数p分别取0.8、0.8、0.9取得较好的分类结果。

从表中可以看出，对于LSB替换算法、LSB匹配算法以及nsf5算法的隐写结果，检测正确率随着嵌入率增大而增大。在LSB替换算法嵌入率为0.1、0.25和0.5 bpp时，本文算法正确率高于文献[16]方法。针对LSB匹配算法以及nsf5隐写算法，本文算法较文献[16]方法在检测正确率上平均提高了3%～4.5%，具有较好的分类效果。

6 结 语

本文提出了一种基于分数阶小波变换的图片隐写分析方法。该方法首先对隐写过后的图像进行DFRWT，将隐写图片映射到分数阶小波域，然后利用PAC提取高频子带信号，计算信息熵，构建敏感特征向量，最后输入到SVM中进行检测。同经典的spam隐写分析方法进行实验对比，实验结果表明，该方法提高了检测正确率。

[1] 黄炜,赵险峰,冯登国,等.基于主成分分析进行特征融合的JPEG隐写分析[J].软件学报,2012,23(7):1869-1879.

[2] Chen D Y,Zhong S P.A Universal Steganalysis Algorithm for JPEG Image Based on Selective SVMs Ensemble[J].Advanced Materials Research,2012,532-533:1548-1552.

[3] Wei J,Wang D.Steganalysis of LSB replacement based on wavelet transform[J].Journal of Tsinghua University,2007,47(4):595-598.

[4] Qin J,Sun X,Xiang X.Steganalysis Based on Lifting Wavelet Transform for Palette Images[C]//International Conference on Computational Intelligence and Security Workshops.IEEE,2007:672-675.

[5] Wang Y,Moulin P.Optimized Feature Extraction for Learning-Based Image Steganalysis[J].IEEE Transactions on Information Forensics & Security,2007,2(1):31-45.

[6] Zhou Z P,Zhang X X,Hui M M.Steganalysis based on wavelet packet transform and genetic algorithm[J].Systems Engineering-Theory & Practice,2010,30(10):1864-1869.

[7] Omrani L,Faez K.Universal JPEG steganalysis based on special frequency regions from wavelet transform[C]//International Symposium on Telecommunications.IEEE,2012:971-975.

[8] Mendlovic D,Zalevsky Z,Mas D,et al.Fractional wavelet transform[J].Applied Optics,1997,36(20):4801-4806.

[9] Huang Y,Suter B.The Fractional Wave Packet Transform[C]//Digital Signal Processing Workshop Proceedings,1998:399-402.

[10] XU Xiaojun,Wang Y R.Novel Image Denoising Method Based on Discrete Fractional Orthogonal Wavelet Transform[J].Tien Tzu Hsueh Pao/acta Electronica Sinica,2014,42(2):280-287.

[11] Shi J,Zhang N T A.A novel fractional wavelet transform and its applications[J].Science China Information Sciences,2012,55(6):1270-1279.

[12] Neeti N,Eastman J R.Novel approaches in Extended Principal Component Analysis to compare spatio-temporal patterns among multiple image time series[J].Remote Sensing of Environment,2014,148:84-96.

[13] Lu K,Xie J,Shu J.A Fast Training Method for Transductive Support Vector Machine in Semi-supervised Learning[M]//High Performance Computing and Applications.Springer International Publishing,2015.

[14] Dai H,Zheng Z,Wang W.A new fractional wavelet transform[J].Communications in Nonlinear Science & Numerical Simulation,2016,44:19-36.

[15] BOSS.base[OL].(2011-5).http://boss.gipsa-lab.grenoble-inp.fr/.

[16] Pevny T,Bas P,Fridrich J.Steganalysis by subtractive pixel adjacency matrix[J].IEEE Transactions on Information Forensics & Security,2010,5(2):215-224.

IMAGESTEGANALYSISBASEDONFRACTIONWAVELETTRANSFORM

Zhao Hongtu Liu Fang Hou Shouming

(CollegeofComputerScienceandTechnology,HenanPolytechnicUniversity,Jiaozuo454000,Henan,China)

In order to improve the detection performance of the existing image steganography algorithm, a novel image steganalysis algorithm based on fractional wavelet transform is proposed. First, the image was simply mapped into the time-frequency domain of the fractional wavelet by two-dimensional fractional wavelet transform. Then, principal component analysis was used to extract the principal component characteristic statistics of the high frequency subbed in the time-frequency domain, the principal component information entropy was calculated, and the sensitive feature was constructed. Finally, extraction features in this paper were classified by a support vector machine. Through the simulation experiment, this paper used the presented algorithm to detect the steganalysis results in multi-rate of three kinds of steganography algorithm. Simulation results show that the proposed algorithm can effectively improve the accuracy of steganalysis.

Steganography Steganalysis Fractional wavelet transform Principal component analysis Support vector machine

2016-12-19。国家自然科学基金项目(61503124)；河南省高校科学技术研究重点项目(15A520016，15A520070)。赵鸿图，副教授，主研领域：电力市场与信息处理。刘芳，硕士生。侯守明，教授。

TP3

A

10.3969/j.issn.1000-386x.2017.11.053