基于RSSI测距定位算法的研究和改进

何沃林

摘要：RSSI的定位算法在实际应用中的定位精度较低。通过研究分析通信距离、环境参数和信号干扰等各种因素对RSSI值测量的影响，为提出高效的定位算法提供研究思路。结合缩短通信距离、改进节点坐标计算方法等几种方法的综合应用，实现对RSSI定位算法的改进和参数优化，提高其定位精度和抗干扰能力。通过对RSSI定位算法的改进和参数优化，提高其定位精度和抗干扰能力。

关键词：无线传感器网络；测距；RSSI；定位算法

中图分类号：TP273 文献标识码：A 文章编号：1007-9416（2017）09-0134-02

接收信号强度测距法RSSI（Received Signal Strength Indication）为基础的定位算法，被普遍运用于无线传感器网络节点定位之中。其理想情况是定位结果坐标为一个正确的位置点，但由于传输距离、信号干扰等诸多因素的影响，往往无法确保RSSI测量结果的精确度，使定位点位于一个存在一定误差的区域内，改正思路是在实际的应用中，对传统的RSSI定位算法进行改进和参数的优化，尽可能缩小这个误差区域。

1 影响RSSI定位精度的因素

1.1 通信距离与障碍物

通信距离将影响到无线电信号衰减量，在长距离传输过程中，信号受环境干扰较大。另外信道内存在障碍物，通过对信号的折射、反射等，会使得信号衰减不断加剧，最终也会对RSSI数值测量结果产生影响。在以下实验过程中，对四组典型环境参数进行选取，A均取值为41，n则分别取值为2.6、2.8、3.0以及3.2。具体结果参见图1。可以看到，在测距距离不断加大的同时，各组环境参数之下的误差曲线均体现出误差持续增加的特性。若保持在5米之内，则误差增长相对缓慢，而一旦超过这一数值，则误差的增加将极为显著[1]。

此外，因为障碍物存在于信道之中，往往会产生反射、折射等影响，在加大通信距离之后，上述影响将因此而增大。RSSI数值的测量将因为障碍物而受到影响，导致传播进程中的信号损耗。

1.2 环境参数

在对RSSI数值进行计算时，所应用的环境参数是否和实际环境相符，是决定定位误差大小的关键。在上述不同通信距离定位误差测试的实验中，当参数A以及n分别为41以及2.8时，则此时获得的定位结果精确度最高，而当参数A以及n分别为41以及3.2时，则取得的定位结果精确度最差[1]。

由此可认识到，定位精确度很大程度上会因为微小的环境参数变化而受到影响。从室内环境来看，障碍物会把室内空间分隔成多个相对独立的子区域，使用单一的环境参数无法适用于整体区域。

1.3 信号干扰

（1）突发干扰。测量RSSI值时，不论是环境的突然改变、还是人员走动等，均会对此产生突发干扰。因为突发干扰的存在，对RSSI值产生了显著影响，且比障碍物存在于信道时的影响程度明显更高。

（2）隨机干扰。信号在传播过程中受到信号反射、衍射以及测量节点内部噪声和量化噪声等因素的影响，使得节点测量获得的RSSI数值产生随机误差[2]。在RSSI测量进程中，随机干扰持续存在，使测量值不断波动，而且因为无规则变化，使得其数值的正负、大小等无法被预测[2]。

（3）噪声干扰。RSSI值测量的整体进程均会受到噪声影响，使得最终获得的是噪声和测量值混合后的数据[3]。对比随机干扰导致的RSSI数值波动，噪声干扰之下的数值波动显然更强，而导致较大脉冲的出现，数据变化更无规律可循[3]。

2 RSSI定位算法的改进和优化

2.1 通信距离和区域布局的调整

从上面的实验数据可以看出，当通信距离达到5米以上时，则将出现显著的定位误差增加，5米距离之内的定位误差增长相对缓慢。通过结合对参考节点密度的增加，使得两类节点的通信距离得以缩短，同时划分整体区域为多个子区域，以5米作为衡量其大小的具体依据[1]。在分割子区域以后，未知节点需符合如下要求，即至少和三个小于5米临界距离的参考节点相互通信，图2为子区域分割的示意图。

在具体运用时，需结合室内整体布局，对子区域的分割方案予以合理设计，尽量减少由障碍物导致的影响。在通信距离方面只需保持在临界距离以内，不需要对子区域进行完全相等的划分。在分割区域以后，在拟合环境参数时，以各子区域作为操作环境，最终获得的环境参数和子区域相符。

2.2 环境参数自适应

为使系统具备和实际环境较为接近的信号衰减模型参数，当网络之中全部参考节点已经加入，未知节点广播信号以前，设置为环境参数的自适应阶段。对距离已知的参考节点进行测量，并校准信号衰减模型的所有参数[4]。

在选取的测距公式之中，在对A值进行测量时，要将参考节点设定为圆心，在半径为1米的圆周之上，有多个参考节点平均分布，随后对圆周之上全部参考节点的RSSI值进行测量，并进行平均值求取，具体参见如下公式（1）。

n为传播损耗系数，环境因素的影响很大，属于一种需重点修正的参数。由于参考节点位置坐标已知，通过和附近的参考节点测距后，就会得到N个到附近参考节点的距离值，即可对N个传播损耗系数n进行计算，同时求取平均值。另外，RSSI值在不同时间内也会有一定波动产生，在参数n进行计算以前，需要对不同时间段的RSSI值进行收集，以其平均值开展计算工作，具体参见式（2）：

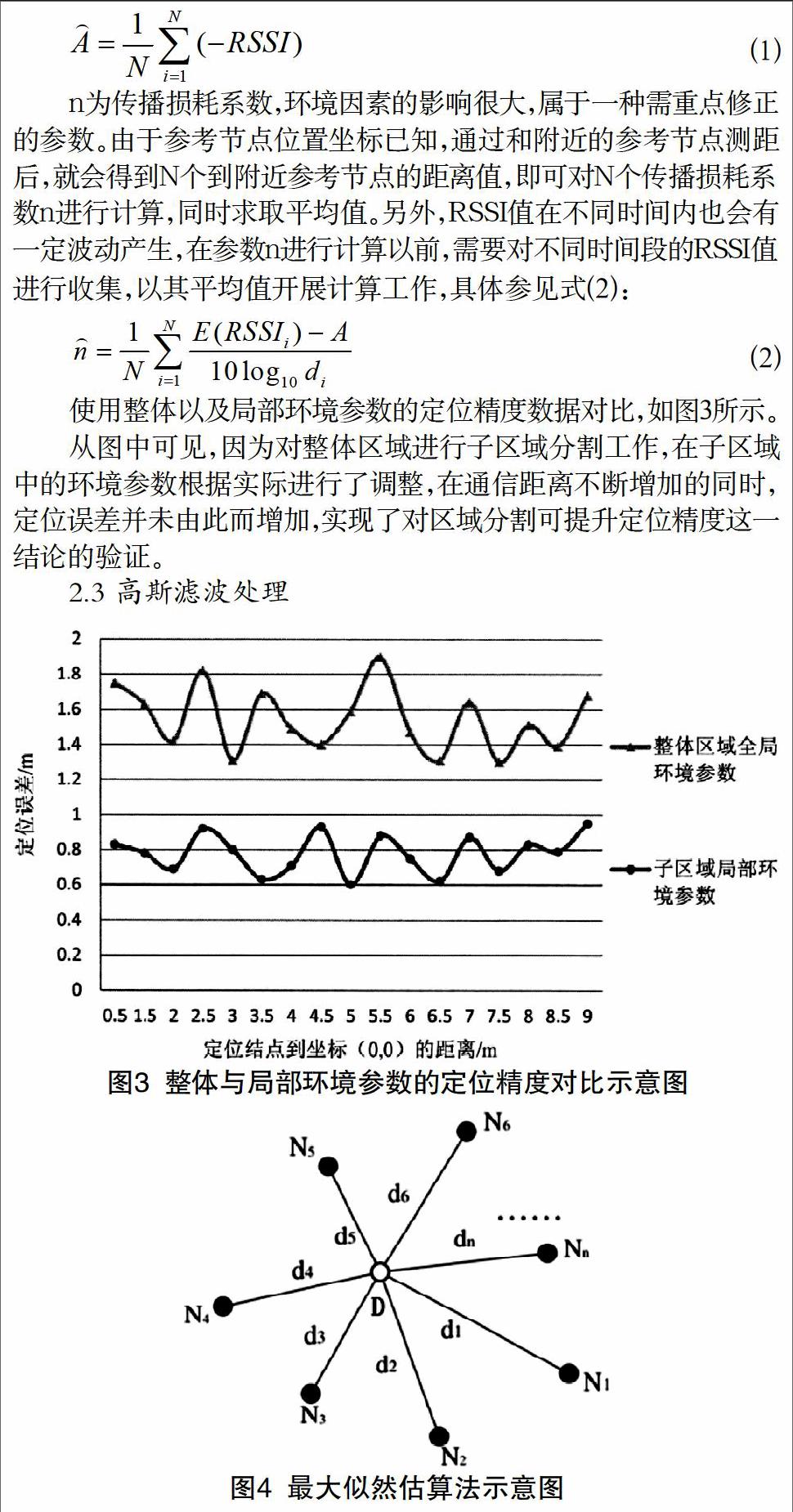
使用整体以及局部环境参数的定位精度数据对比，如图3所示。

从图中可见，因为对整体区域进行子区域分割工作，在子区域中的环境参数根据实际进行了调整，在通信距离不断增加的同时，定位误差并未由此而增加，实现了对区域分割可提升定位精度这一结论的验证。

2.3 高斯滤波处理

结合研究数据得出，在某个位置之上同一节点获得的RSSI数值，其误差存在随机性，符合或近似符合正态分布，通过高斯模型的运用，对高概率区的RSSI数值进行选取，可使得大干扰、小概率事件对RSSI值测量的影响得以减少，也让定位变得更为准确。对应的高斯密度分布函数见式（3）、（4）、（5）所示。endprint

在发生概率相对较高的区域，即概率超过0.6（经验值）的范围进行选取，如式（6），过滤了因为干扰而导致的误差较大的RSSI测量值。

本方法的软件编程设计思路较为简单，也就是在未知节点将n组数据快速的发送给参考节点，由参考节点在相应数组Rssi—val[ ]内进行存储，再结合高斯模型来开展数据滤波处理工作。系统的临界值为0.6，结合高斯密度分布函数公式，可对概率结果进行输出，然后在最终确认数组Rssi_val_gauss[ ]内存放。在处理数据并进行存储操作之后，结合式（7）即可对几何均值进行求取[5]。

3 节点坐标计算方法的改进

3.1 采用最大似然估算法

研究证明，实际的信号传输损耗符合对数-正态分布阴影模型，参见式（8）：

Xσ是一个标准偏差为σ、平均值为0的正态随机变量 。

设在dO处的信号强度为A，Xσ的平均值为0，通过简化后得到式（9）可知：

在分析测距模型之后可认识到，RSSI实际上是一个正态随机变量，其标准偏差为σ。从矩阵相关理论分析，在符合正态分布的情况下，则最小二乘法和最大似然估算法具有相同的计算结果，均属于最小均方差时的最优解[6]，所以选用最大似然估算法，如图4所示.它需要三个或以上的参考节点来计算未知节点的坐标，通过对参考节点的RSSI均值的大小进行排序，选取最强的几个信号进行定位计算，让定位误差得到显著减小。

3.2 定位结果修正

通过定位计算得到的节点位置坐标，一般都和实际位置存在一定的误差，任意一次定位结果均带有随机性，但都是以实际位置为中心而产生的一些相应偏差。为减少定位误差，可以通过多次測量和迭代的方法，对定位结果进行修正。可以采用迭代去噪法参见式 （10），主要结合第k+1的测量值以及第k次的估算值，对第k+1次估算值进行计算，不仅简单，且效果显著，实现起来较为容易[6]。

4 结语

RSSI的定位算法的无线定位系统，不论是功耗、还是硬件需求等方面都是最低的，而且传感器节点本身就具有无线信号收发能力，市场上多种常见的无线通信模块可以在不添加任何硬件的条件下测出RSSI值。因此RSSI是一种容易实现、成本低、复杂度低的无线测距方法，其技术和市场已经相当的成熟，后期可以在实际使用环境的基础上，通过对RSSI定位算法的改进和参数优化，提高其定位精度和抗干扰能力。

参考文献

[1]张苍松.基于RSSI的室内定位算法优化技术[D].西北大学，2014.

[2]Abousetta M M，Cooper D C. Noise analysis of digitised FMCW radar waveforms[C]//Radar， Sonar and Navigation， IEE Proceedings.IET，1998，145（4）：209-215.

[3]李冰.射频信号噪声消除与抑制研究[D].大连理工大学，2009.

[4]孟东阳，何秀凤，桑文刚.基于无线网络传感器的定位技术研究[J].电子测量技术，2012，（09）：10-15.

[5]黄勇，徐耀，曾刚，王波，黄林.基于无线传感器网络的室内停车场定位系统研究[J].湖北民族学院学报（自然科学版），2014，32（01）：102-105.

[6]郭金铭，邹刚伟，胡斌杰，曹国雄.基于ZigBee的无线传感器网络定位技术研究[J].移动通信，2013，（18）：74-79.endprint