一类具有时滞的经济模型Hopf分岔*

王嘉薇

(安徽财经大学金融学院，安徽 蚌埠 233030)

一类具有时滞的经济模型Hopf分岔*

王嘉薇

(安徽财经大学金融学院，安徽 蚌埠 233030)

利用特征值方法，讨论了一类具有时滞的宏观经济模型局部渐近稳定和局部Hopf分岔的存在性，得到模型产生局部Hopf分岔的时滞临界点.研究表明，有效控制或者延迟Hopf分岔的产生，有利于市场的健康发展.最后利用仿真示例，验证了所得结果的正确性.

时滞；经济模型；Hopf分岔

引言

在微分方程的定性理论中，稳定性和分岔理论作为其中的一个重要分支，受到国内外众多研究学者的关注，尤其是在捕食系统模型、传染病模型方面取得了诸多成果[1～3].近年来，有不少研究学者，利用微分方程稳定性理论和分岔理论中的成果，对能源价格模型[4,5]、经济学模型[6]进行了深入研究.文献[7]根据具有疾病的捕食系统模型提出下列关于投资企业之间的一类经济模型：

(1)

其中，x(t)表示投资项目在时刻t的数量，y1(t)表示正常运营的投资公司在时刻t的数量，y2(t)表示面临倒闭的投资公司在时刻t的数量.r1,r2,b1,b2,d1,d2,a,和c均为模型(1)的系数，并且均为正常数.其中，r1(r2)表示投资项目(正常运营的投资公司)的自然增长率；b1(b2)表示投资项目与正常运营的投资公司(面临倒闭的投资公司)之间的作用系数；d1(d2)表示正常运营的投资公司(面临倒闭的投资公司)的自然衰退率；a表示投资项目受已有项目数的抑制系数；c表示正常运营的投资公司因获得投资项目而具有的发展率.文献[8]在模型(1)的基础上增加了宏观调控，得到具有宏观调控的时滞经济模型：

(2)

其中，τ为投资项目的成熟期时滞，K为国家对投资项目宏观调控的作用系数.文献[7]研究了模型(2)的稳定性.但是文献[7]忽略了一点，即正常运营的投资公司走向倒闭，需要经过一个过渡期.基于此，本文在模型(2)的基础进一步引入正常运营的投资公司向面临倒闭的公司过渡期时滞，得到下列具有两个时滞的宏观经济模型：

(3)

其中，τ1为投资项目的成熟期时滞，τ2为正常运营的投资公司向面临倒闭的公司过渡期时滞.本文只讨论当τ1=τ2的情形.当τ1=τ2时，模型(3)变为

(4)

本文主要以时滞τ为分岔参数，利用文献[9]中的Hopf分岔定理讨论模型(4)Hopf分岔的存在性.

1 Hopf分岔的存在性

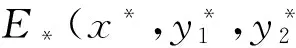
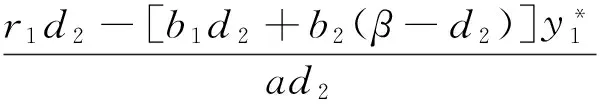
(5)

其中，

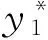
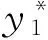
λ3+A2λ2+A1λ+A0+(B2λ2+B1λ+B0)e-λτ+(C1λ+C0)e-2λτ=0.

(6)

其中，

A0=a1a6a7+a2a4a8-a1a5a8,

A1=a1a5+a1a8+a5a8-a2a4-a6a7,

A2=-(a1+a5+a8),

B0=a1a6b2+a2a4b3-a3a4b2-b1(a6a7+a5a8+a1a5),

B1=b1(a5+a8)+b3(a1+a5)-a6b2,

B2=-(b1+b3),C0=a6b1b2-a5b1b3,C1=b1b3,

在方程(6)左右两边同时乘以eλτ，方程(6)变为下列形式

B2λ2+B1λ+B0+(λ3+A2λ2+A1λ+A0)eλτ+(C1λ+C0)e-λτ=0.

(7)

当τ=0时，得到

λ3+(A2+B2)λ2+(A1+B1+C1)λ+A0+B0+C0=0.

(8)

显然，根据赫尔维茨稳定性判据可知，当A0+B0+C0>0,A2+B2>0，且(A2+B2)(A0+B0+C0)>A1+B1+C1时，方程(7)的根均具有负实部.此时模型(4)局部渐近稳定.

当τ>0时，令λ=iω(ω>0)为方程(7)的根，则有

(9)

其中，

P1(ω)=C1ω-A1ω+ω3,P2(ω)=C0+A0-A2ω2,

P3(ω)=B2ω2-B0,P4(ω)=C1ω+A1ω-ω3,

P5(ω)=C0-A0+A2ω2,P6(ω)=-B1ω.

因此，根据方程(9)，有

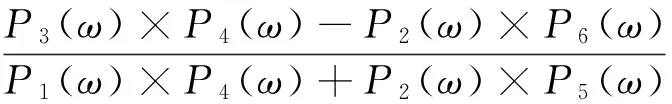
根据sin2(τω)+cos2(τω)=1，并且sin(τω)和cos(τω)的表达式已知，可以得到下列关于ω的代数方程

[P3(ω)×P4(ω)-P2(ω)×P6(ω)]2+[P1(ω)×P6(ω)+P3(ω)×P5(ω)]2
=[P1(ω)×P4(ω)+P2(ω)×P5(ω)]2

(10)

对方程(7)左右两边同时求λ关于τ的导数，可以得到

(11)

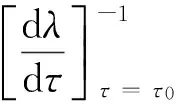
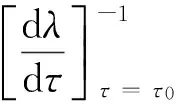
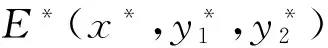
2 仿真示例

为了验证以上本文所得结果的正确性，我们给出一个仿真示例.选取文献[7]中相同的参数值：r1=r2=0.1,a=0.1,b1=b2=0.5,c=0.5,d1=0.36,d2=0.1,β=0.3,K=0.5.考虑如下示例：

(12)

根据文献[7]的计算结果可知，示例模型(12)存在唯一正平衡点E*(0.019 6,0.065 4,0.130 7).借助于Matlab软件容易验证当τ=0时，示例模型(12)的正平衡点E*(0.019 6,0.065 4,0.130 7)是局部渐近稳定的.当τ>0时，计算得到ω0=0.296 2，τ0=1.596 0.因此，当τ∈[0,τ0=1.596 0)时，E*(0.019 6,0.065 4,0.130 7)是局部渐近稳定的，仿真效果如图1所示.当τ>τ0=1.596 0时，E*(0.350 3,0.346 7)失去稳定性，并在τ0=1.596 0时产生Hopf分岔，以及分岔周期解.仿真效果如图2所示.另外，如果K=0，对于模型(4)来说，如果国家不对投资项目进行宏观调控的情况下，可以计算得到τ00=12.728 9.相应的仿真效果如图3～4所示.因此，可以看出，宏观调控政策对于维持市场稳定持续发展，的确起到了一定的积极作用.

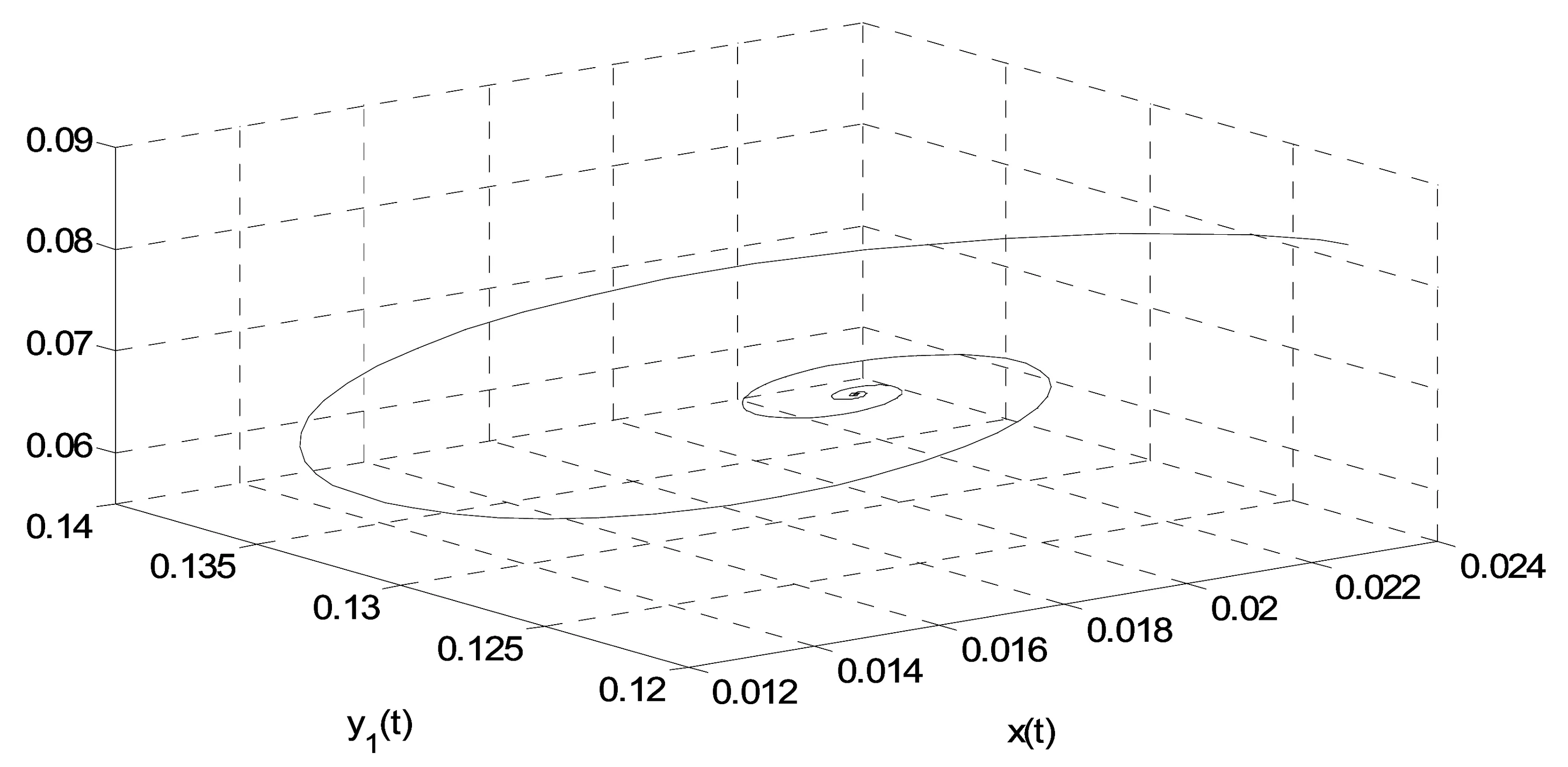
图1 当K=0.5,τ=1.05<τ0时，E*(0.019 6,0.065 4,0.130 7)局部渐近稳定

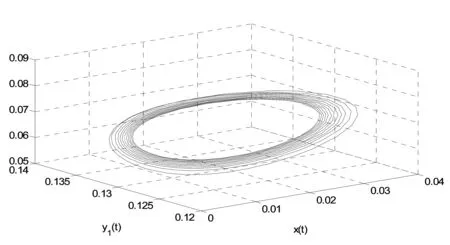
图2 当K=0.5,τ=1.73>τ0时,E*(0.019 6,0.065 4,0.130 7)失去稳定并产生Hopf分岔

图3 当K=0,τ=8.65<τ00时，E*(0.019 6,0.065 4,0.130 7)局部渐近稳定

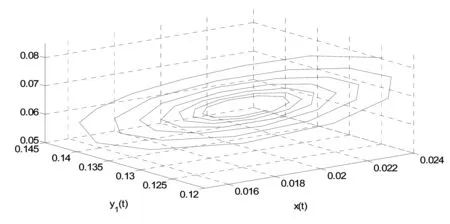
图4 当K=0,τ=21.85>τ00时，E*(0.019 6,0.065 4,0.130 7)失去稳定并产生Hopf分岔

3 小结

本文在文献[7]的基础上，进一步引入了正常运营的投资公司向面临倒闭的公司过渡期时滞，研究了另外一种情形的具有时滞的宏观经济模型.首先，以时滞为分岔参数，通过分析模型相应特征方程根的分布情况，讨论了Hopf分岔的存在性，给出模型局部渐近稳定和产生Hopf分岔的充分条件.研究表明，国家出台宏观调控政策，的确有利于保持市场的持续稳定发展，所得结果和文献[7]一致.同时，本文又在文献[7]的基础上，研究了另外一种时滞对模型稳定性的影响,所得结果又是对文献[7]的适当补充.

[1]Song Y. L, Yuan S. L, Zhang J. M. Bifurcation analysis in the delayed Leslie-Gower predator-prey system [J]. Applied Mathematical Modelling, 2009,33 (11) 4049-4061.

[2]李冰，王辉，胡志兴，等.具有第IV类功能反应函数的捕食系统 [J]. 河南大学学报(自然科学版), 2016,46 (5): 618-625.

[3]魏凤英，蔡裕华，赵延辉. 具非线性发病率随机SIQS传染病模型的渐近行为[J].生物数学学报，2016,31(1):109-117.

[4]薛婷婷，樊小琳，李坚,等.一类时滞能源价格模型解的振动性[J].四川师范大学学报:自然科学版，2016,39(1):65-70.

[5]薛婷婷，樊小琳，李坚,等.一类时滞能源价格模型解的稳定性[J].数学的实践与认识，2015,45(4):248-255.

[6]梁玉麟，赵建东.基于Logistic方程的供应商-采购商合作关系的经济模型研究[J].鲁东大学学报(自然科学版),2015,31(3):200-204.

[7]Xiao Y N, Frank V D. The dynamics of an eco-epidemic model with biological control [J]. Ecol Modelling, 2003,168(1):203-214.

[8]谈晓芬，李庶民. 含有时滞的宏观经济模型的稳定性分析[J].曲阜师范大学学报,2016,42(1):1-9.

[9]Hassard B. D, Kazarinoff N. D, Wan Y. H, Theory and Applications of Hopf Bifurcation [M]. Cambridge University Press, Cambridge, 1981.

HopfBifurcationofaTime-delayEconomicModel

WANG Jia-wei

(School of Finance, Anhui University of Finance and Economics, Bengbu Anhui 233030, China)

Using eigenvalue method, the paper discusses the existence of partial asymptotic stability and partial Hopf-bifurcation in a class of macroeconomic models with time delay and obtains the delay critical point of bifurcation. Studies have shown that effective control or delay of Hopf-bifurcation is beneficial to the healthy development of the market. Finally, a simulation example is given to verify the correctness of the obtained results.

time delay; economic model; Hopf-bifurcation

1673-2103(2017)05-0060-05

2017-06-10

2016年度安徽省自然科学基金青年项目(1608085QF145)

王嘉薇(1996-)，女，安徽马鞍山人，研究方向：货币金融学.

O175.12

A