面向故障扰动的舰面保障重调度仿真研究

蒋婷婷，韩 维，苏析超

(海军航空工程学院 飞行器工程系， 山东 烟台 264001)

面向故障扰动的舰面保障重调度仿真研究

蒋婷婷，韩 维，苏析超

(海军航空工程学院 飞行器工程系， 山东 烟台 264001)

针对舰载机舰面保障过程中设备故障扰动下的重调度问题，综合考虑保障的工序逻辑约束和人员、设备等资源约束，提出了舰载机保障重调度预判机制，建立了舰载机舰面保障重调度模型，并采用变邻域算法对模型进行求解。仿真结果表明，重调度预判机制可以进一步节省重调度保障时间，变邻域算法求解速度可以满足任务需求。该重调度模型和算法能够在任务要求保障完工时间内，高效解决由于保障工序故障而导致的舰载机舰面保障重调度问题。

舰载机；舰面保障；重调度优化；变邻域算法

舰载机甲板保障调度是指在时间、空间、资源及工序逻辑等多重约束下对舰载机进行维护保障。由于实际保障调度过程中一直存在动态扰动，因此对该过程的优化对提升舰载机出动架次率有重要影响。

国内外关于舰载机动态调度的研究主要集中在实时调度方面。美国麻省理工学院的Michini[1]和Ryan[2]等联合开发了航母甲板作业规划决策支持系统(deck operations course of action planner，DCAP)，以进行基于人机交互的智能决策。文献[3-5]考虑了舰载机故障等动态因素，提出了基于多主体系统(MAS)技术的实时动态调度模型。文献[6]基于系统动力学理论建立了舰载机动态调运复杂时变系统的存量流量图及数学模型。文献[7]建立了基于层次任务网络(HTN)的动态甲板任务规划系统，可对任务变化做出实时响应。在重调度方面，文献[8]分析了作战任务变更对舰载机航空保障调度的影响，采用重调度理论研究了基于任务的连续出动舰载机航空保障重调度模型。

在对舰载机进行保障时，一旦发生设备故障，保障的组织实施便会发生相应改变，因而需要根据当前状态进行重调度，即在初始调度方案执行基础上，根据发生的故障对后续工序开始时间安排和资源分配进行重新调度。

1 舰面保障重调度问题建模

1.1 问题描述

故障扰动导致的保障重调度涉及到大量人员、设备的重新分配，造成整个保障的任务量和难度显著增加。本文建立了重调度预判机制，重调度预判流程见图1。

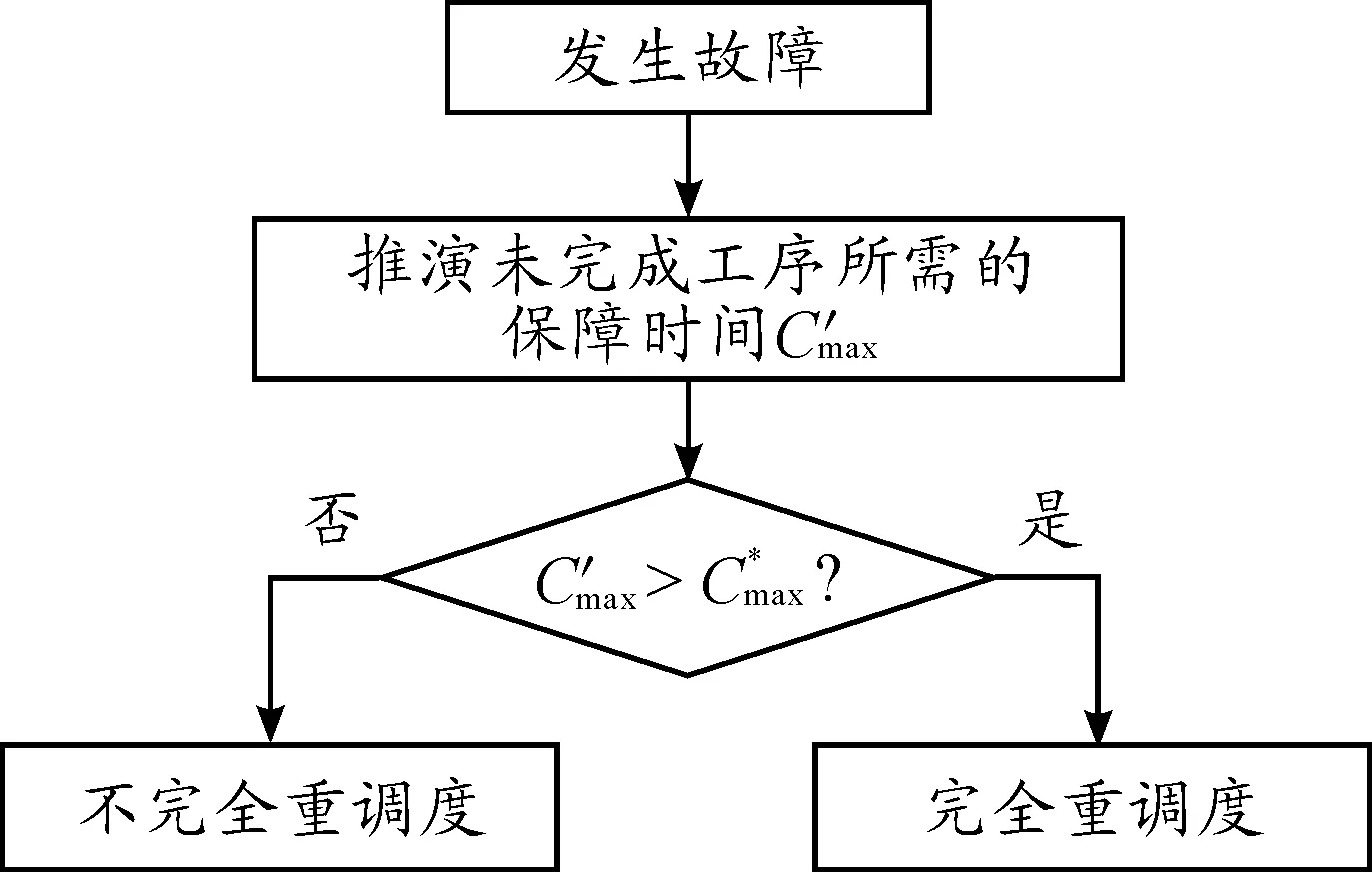
图1 重调度预判流程

进行完全重调度仿真时，故障时刻正在执行的工序按照原初始计划进行，以满足最小保障完工时间为目标，对未开始执行工序进行重调度，确定每个舰载机每道工序进行保障时的开始时间及人员、设备分配情况，高效地辅助保障指挥管理人员制定满足保障需求的保障调度计划。

1.2 符号定义

定义模型参数如下：

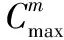
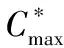
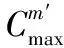
I为舰载机i的集合；

Ji为舰载机i的工序集合；

Oij为第i架舰载机的第j道工序；

Sij为工序Oij的保障开始时间；

EXi为舰载机i入场系留完毕时间；

Pij为工序Oij的前驱任务集合；

dij为工序Oij的工期；

Kp为保障人员专业种类集合；

Lpk为第k(k∈Kp)类专业保障人员集合；

rpijk为工序Oij所需第k(k∈Kp)类专业保障人员的数量；

Kr为保障设备种类集合；

Lrk为第k(k∈Kr)种设备保障单元集合；

reijk为工序Oij所需第k(k∈Kr)种保障设备的数量；

Kw为消耗性资源种类集合；

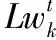
rwijk为Oij所需第k(k∈Kw)类消耗性资源的数量；

变量Oij(t)当工序Oij在t时刻处于执行状态则为1，否则为0；

变量Xpijkl当工序Oij分配给第l(l∈Lpk)个保障人员时则为1，否则为0；

变量Xeijkl当工序Oij分配给第l(l∈Lrk)个保障设备时则为1，否则0。

1.3 数学模型

目标函数如下：

(1)

约束条件如下：

Si1≥EXi, ∀i∈I

(2)

(3)

(4)

(5)

Sij≥Sih+dih,∀h∈Pij,∀i∈I,∀j∈Ji

(6)

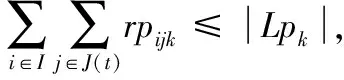
(7)

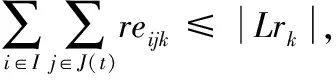
(8)

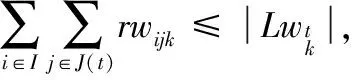
(9)

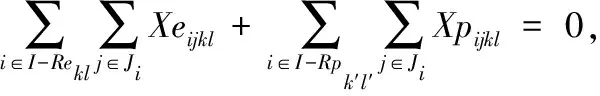
∀j∈Ji,∀k∈Kr,∀l∈Lrk,

∀k′∈Kp,∀l′∈Lpk

(10)

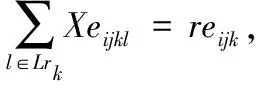
(11)

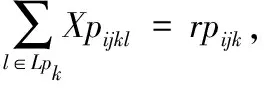
(12)

式(1)代表目标函数为最小化完全重调度保障完工时间。其中

(13)

式(2)～式(12)表示约束条件。式(2)表示第i架舰载机入场系留完毕后才能开始保障，j=1代表开始的虚工序；式(3)～式(5)动态地表示舰载机各工序、人员、设备的状态，且表示保障过程中已经开始的保障活动不允许中断；式(6)表示各舰载机工序的紧前关系约束；式(7)～式(9)分别代表人员、设备和消耗性资源的数量约束，即任一时刻所有处于执行状态的工序对它们的需求量小于其数量上限；式(10)为设备及人员的保障范围约束，即只对在保障设备及保障人员的保障范围之内的舰载机进行保障；式(11)～式(12)分别表示设备和人员需求匹配约束，即被分配数量应等于其需求量。

2 变邻域算法

Mladenovic和Hansen[9]于1997年提出了变邻域算法(Variable Neighborhood Search,VNS)，其基本思想是：构造多个邻域结构，在一个邻域结构内搜索局部最优解，当局部搜索陷入局部最优时，通过系统地改变邻域结构寻找最优解。相对于传统的固定邻域搜索算法，基于多邻域结构集的系统变化拓展搜索范围，搜索能力更强，而且VNS算法无需调整参数，实现简单，因而在组合优化领域得到了广泛应用。

2.1 编码和解码

本算法采用基于开始时间的优先数编码[10]，即序列中的每个元素固定表示调度任务时的优先权，在调度时根据任务优先权的大小决定任务调度顺序，一般将每个元素初始化为[0,1]的随机数，本文将每道工序的开始时间作为优先数。根据上述模型表示为X=[S11S12…S1|J1|S21…Sij…Sn|Jn|]，其中，Sij为第i架舰载机第j道工序的开始时间，用以表示编码中的优先数。

对个体进行解码通常采用串行调度生成方案(Serial Schedule Generation Scheme,SSGS)或并行调度生成方案(Parallel Schedule Generation Scheme,PSGS)。本文在考虑拓扑序列和资源约束的情况下，提出了一种先串行调度后并行分配的两阶段解码方案，首先仅考虑人员的数量限制，不考虑其分配，采用SSGS产生工序调度方案，确定了每道工序的起止时间，其中设备的选择采用基于覆盖范围内剩余工序作业时间最少优先规则(MTRCA)[11]；第二阶段，考虑人员负载均衡性，基于各工序开工时间和PSGS机制，按时序由小到大并行递推为各工序分配保障人员，在每一个决策时刻，优先选取累积保障时间最少的人员，生成最终的保障调度和人员分配方案。

2.2 邻域结构

设计VNS算法首要问题是设计最优解的邻域。根据舰载机保障重调度问题的特点，采用了四种产生最优解邻域的方法，除了两点交换Swap和插入Insert这两种基本的邻域结构外，本文设计了另外两种复合邻域结构：邻域结构中的每个复合动作均由毁坏动作和重建动作(Ruin amp; Recreate，Ramp;R)两个动作构成，毁坏动作代表将从序列中移除部分元素，重建动作表示对这些元素进行打乱重排后，再将它们重新插入返回序列中。两种复合邻域结构的区别在于进行毁坏重建的范围，即进行毁坏重建的元素数量，这决定了序列变化的强度。

1) 两点交换Swap。随机产生两个交换位置，并交换两个位置上的元素。

2) 插入Insert。随机产生两个元素位置，将位置序号大的元素p插入位置序号小的元素q之前，元素q及其之后的元素按顺序向后顺延。

3) 单架舰载机内工序的毁坏重建Ramp;R1。即从单架舰载机序列中随机产生m个(mgt;2，是整数)元素位置，在考虑工序逻辑关系的前提下，打乱重排这些元素的顺序。

4) 整个重调度工序的毁坏重建Ramp;R2。考虑工序逻辑的条件下，针对重调度的个体X=[S11S12…S1|J1|S21…Sij…Sn|Jn|]随机产生n(ngt;m)个元素进行打乱重排。

前两种邻域结构能对局部区域进行细致搜索，有利于算法的探索能力。Ramp;R2较之Ramp;R1打乱重排的工序更多，因此Ramp;R2会对当前解造成更大的破坏，一定程度上增强了算法的开发能力，利于跳出局部最优。

2.3 算法框架

基于上述4种邻域结构，变邻域搜索算法具体操作步骤如下：

步骤1 确定四种邻域结构Nk(k=1,2,3,4)，进行初始化操作，输入评价次数Q和初始解X，令i=0，最优个体best_X=X。

步骤2 如果满足循环终止条件(igt;Q)，输出最优个体best_X；否则，令k=1。

步骤3 按邻域结构Nk随机产生一个新解X′，比较其与初始解X的适应度值。

步骤4 若f(X′)lt;f(X)，则输出k，令best_X=X′，适应度值小的解代替初始解，并继续在邻域结构Nk内搜索；否则，k=k+1。

步骤5 若kgt;4，则i=i+1，返回步骤2；否则返回步骤3，进入下一个邻域结构搜索。

3 仿真结果与分析

3.1 算例描述

以库兹涅佐夫号航母为实例分析对象，假定某出动任务需要对8架舰载机进行出动前的机务勤务保障作业。设备对舰载机的保障覆盖情况见表1。

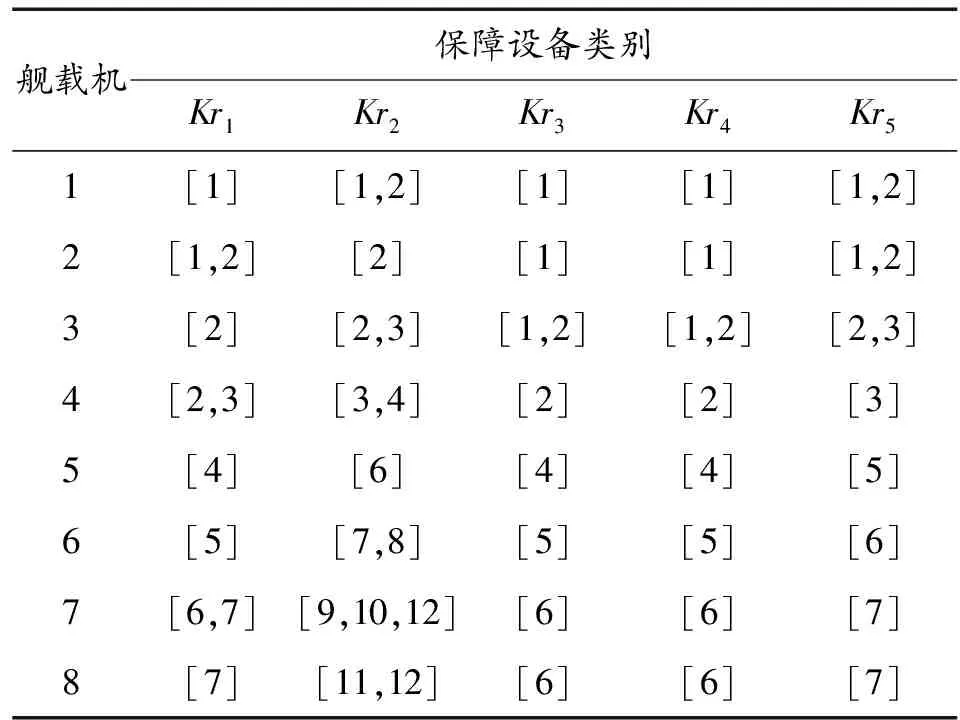
表1 设备对舰载机保障覆盖关系

单机的保障工序流程图如图2所示。图2中：各编号标注为所需保障人员专业类别和设备类型，且需求量均为1，工序3—5—7—12之间虚线连接表示存在站位空间约束。

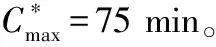
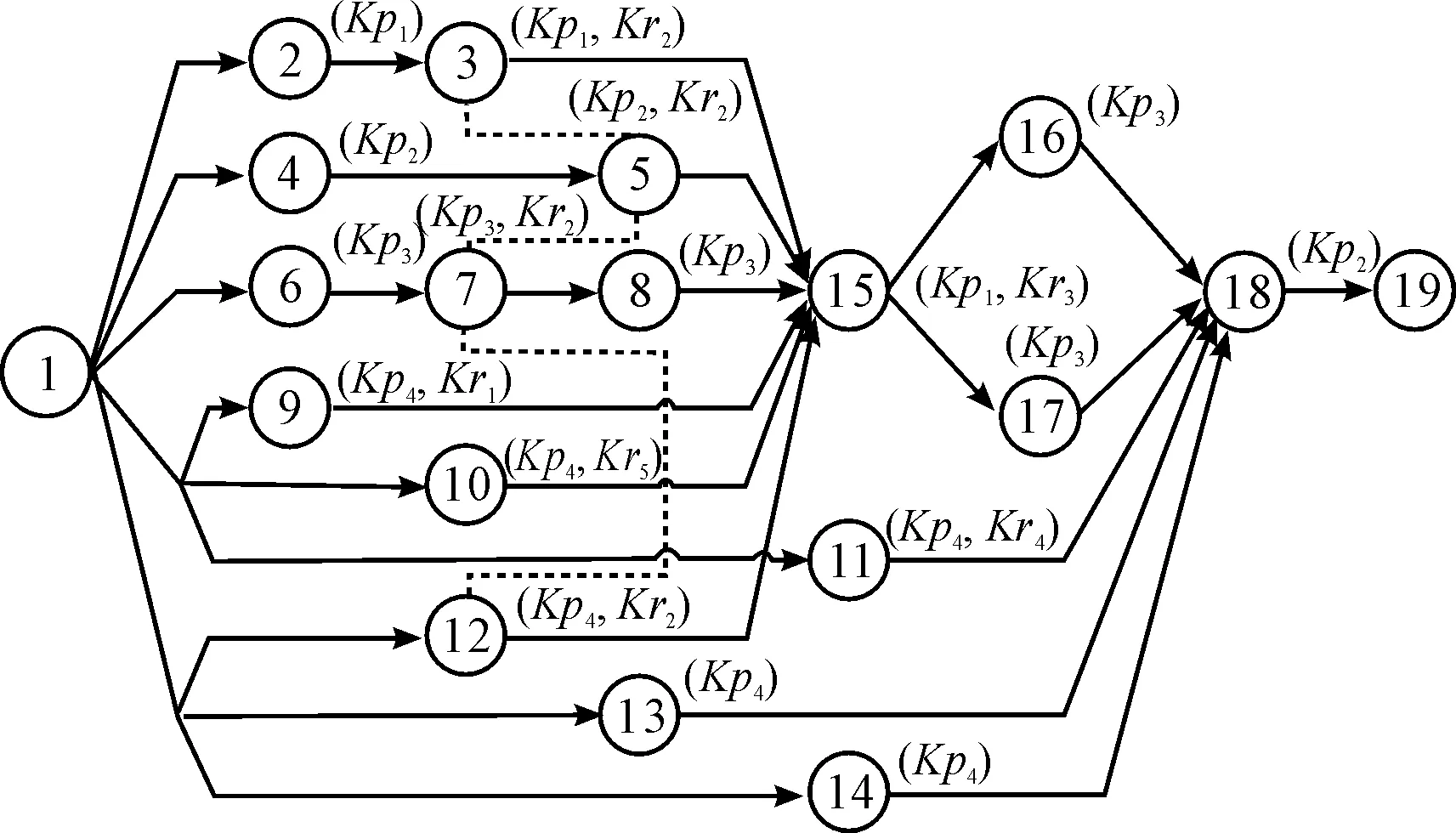
图2 单机保障工序流程

3.2 初始调度

令算法评价次数Q=100，m取[4,8]中的随机整数，n取[9,15]中的随机整数，在2.30 GHz，4.00 GB内存的SONY笔记本上仿真8次所得结果如表2所示。

表2 初始调度仿真结果 min

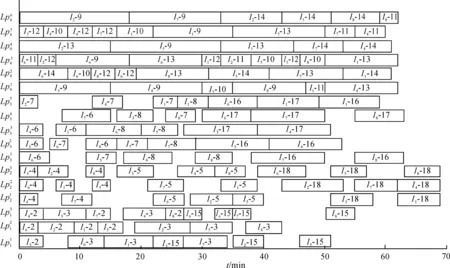
图3 初始调度人员分配甘特图

3.3 重调度预判

本算例随机挑选t=20 min时，第四架舰载机的第18道工序发生故障，其在初始调度中工期为8 min，执行时间段为17～25 min，现令其工期延长为18 min。采用相同的参数进行重调度预判，得到不完全重调度保障时间为76 min，人员分配甘特图如图4所示，仿真耗时不超过1 s。可以看出对比初始调度，每个保障人员分配的工序与初始调度相同，但工序开始时间因为故障工序的原因发生了顺延。由于不完全重调度的时间大于任务要求保障完成时间，因此需要进行完全重调度。

3.4 完全重调度

针对初始调度在t=20 min的时刻进行完全重调度，重调度时刻正在工作的各设备、人员需完成当前工序才能参与重调度，未调度工序则需要在新的初始条件下重新进行分配。采用相同的参数进行仿真，所得最优保障完成时间为69 min，满足任务要求保障完成时间。每次仿真耗时不超过8 s。对应人员分配甘特图如图5所示。

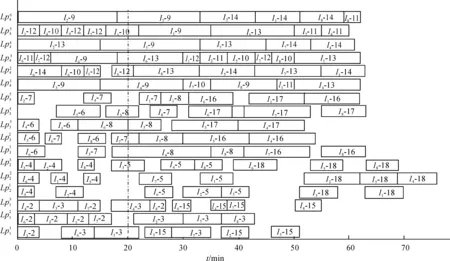
图4 重调度预判人员分配甘特图

图5 完全重调度人员分配甘特图

在故障工序时间延长10 min的条件下，现以表3直观地对各调度状态所需的保障时间进行对比。

表3 各调度状态下保障时间 min

其中右移调度表示故障发生后，所有未调度工序的开始时间整体右移故障延迟时间，在本案例中即为10 min，所以右移调度的调度时间为79 min。表3表明完全重调度效果突出，可以大大缩减工序故障导致的时间推延。

同时，仿真过程中还发现重调度预判的程序运行时间要明显短于完全重调度的程序运行时间，即若预判所得不完全重调度保障完工时间在任务要求保障完工时间之内，即可直接进行不完全重调度，可进一步缩短了重调度的时间，同时避免了实际重调度过程中人员和设备又被重新分配工序导致的混乱。

从图3、图5中可以清楚地看出各保障人员在各个时刻分配到的舰载机工序，各舰载机工序之间的任务优先级也得到了满足，同时满足任务要求的保障时间。因此，利用变邻域算法得到的调度甘特图可以方便地指导舰载机舰面保障调度。

4 结论

本文研究了基于工序故障所引起的舰载机舰面保障重调度问题，在考虑资源约束和工序逻辑约束的条件下，建立了基于重调度预判机制的舰面保障重调度模型，并设计了针对重调度模型的变邻域算法。仿真结果表明，重调度预判机制可以进一步节省重调度保障时间，避免实际调度过程中的工序分配混乱，而变邻域算法也具有较好的探索和寻优性能。该模型和算法能够在任务要求保障完工时间内，高效解决由于保障工序故障而导致的舰载机舰面保障重调度问题。

[1] MICHINI B,HOW J P.A human-interactive course of action planner for aircraft carrier deck operations[J].AIAA,2011:1-11.

[2] RYAN J,CUMMINGS M,ROY N,et al.Designing an interactive local and global decision support system for aircraft carrier deck scheduling[M]//Infotech@ Aerospace 2011.2011:1516.

[3] 冯强,曾声奎,康锐.基于MAS的舰载机动态调度模型[J].航空学报,2009,30(11):2119-2125.

[4] 冯强,曾声奎,康锐.基于多主体的舰载机综合保障过程建模方法[J].系统工程与电子技术,2010,32(1):211-216.

[5] 冯强,曾声奎,康锐.不确定条件下舰载机动态调度仿真与优化方法[J].系统仿真学报,2011,23(7):1497-1501.

[6] 岳奎志,孙聪,罗明强,等.舰载机动态调运系统的运行模型[J].北京航空航天大学学报,2013,39(8):1062-1068.

[7] QI C,WANG D.Dynamic aircraft carrier flight deck task planning based on HTN[J].Ifac Papersonline,2016,49(12):1608-1613.

[8] 魏昌全,陈春良,王保乳.基于任务的连续出动舰载机航空保障重调度研究[J].指挥控制与仿真,2012,34(3):23-26.

[9] MLADENOVI N,HANSEN P.Variable neighborhood search[J].European Journal of Operational Research,2008,191(3):593-595.

[10] DEBELS D,VANHOUCKE M.A decomposition-based genetic algorithm for the resource constrained project scheduling problem[J].Operations Research,2007,55(3):457-469.

[11] 苏析超,韩维,萧卫,等.基于Memetic算法的舰载机舰面一站式保障调度[J].系统工程与电子技术,2016,38(10):2303-2309.

(责任编辑唐定国)

ReschedulingStudyofCarrierAirplaneSupportonDeckUndertheBreakdownDisturbance

JIANG Tingting， HAN Wei， SU Xichao

(Department of Airborne Vehicle Engineering, Naval Aeronautical and Astronautical University, Yantai 264001, China)

In order to solve the rescheduling problem due to equipment breakdown during the carrier airplane support on deck, the topological constraints and resource constraints including crew and equipment are taken into account, and the prognosis for the rescheduling is proposed. Based on this, the rescheduling model of flight deck operations is established, and the Variable Neighborhood Search (VNS) algorithm is used. The simulation results show that the prognosis for the rescheduling can save the great deal of time and the VNS algorithm performs well to satisfy the mission requirements. The rescheduling model and VNS algorithm can effectively solve the rescheduling problem caused by equipment breakdown during the carrier plane support on deck within the required time.

carrier airplane; support on deck; rescheduling optimization; variable neighborhood search algorithm

2017-07-15；

2017-08-10

国家自然科学基金项目(51375490)

蒋婷婷(1995—)，女，硕士研究生，主要从事舰载机航空保障工程研究。

韩维(1970—)，男，博士。教授，主要从事航空保障工程和飞行动力学研究。

后勤保障与装备管理

10.11809/scbgxb2017.11.021

本文引用格式：蒋婷婷，韩维，苏析超.面向故障扰动的舰面保障重调度仿真研究[J].兵器装备工程学报，2017(11):93-98.

formatJIANG Tingting，HAN Wei，SU Xichao.Rescheduling Study of Carrier Airplane Support on Deck Under the Breakdown Disturbance[J].Journal of Ordnance Equipment Engineering,2017(11):93-98.

V271.4+92

A

2096-2304(2017)11-0093-06