指数型有寿件备件需求预测模型

易勇华，傅 健，王春枝，张志华

(1.湖北工业大学 计算机学院， 武汉 430068； 2.中国人民解放军91181部队, 山东 青岛 266405；3.海军工程大学 科研部， 武汉 430033)

指数型有寿件备件需求预测模型

易勇华1，傅 健2,3，王春枝1，张志华3

(1.湖北工业大学 计算机学院， 武汉 430068； 2.中国人民解放军91181部队, 山东 青岛 266405；3.海军工程大学 科研部， 武汉 430033)

针对有寿件工作寿命分布不确定、备件数量难预测的问题，建立了一种基于正态近似的指数型有寿件备件需求预测模型；首先通过贝叶斯理论将有寿件的工作寿命分布近似为正态分布；然后利用正态分布的可加性建立其备件保障概率模型；最后在算例中通过与仿真结果的对比表明：本文模型能较为准确地计算备件需求量及备件保障概率，满足实际工程应用要求。

有寿件；备件需求；备件保障概率；正态近似分布

有寿件是规定了预防性维修更换或报废期限及可以预计使用寿命的一类备件[1]，亦称限寿件。在航空领域，飞机备件通常分为初始备件、后续备件和有寿备件[2]。使用有寿件能有效地预防故障发生，因此在航空领域有寿件的使用与保障问题具有重大的现实意义。

有寿件的保障问题实质上是预防性维修和修复性维修相结合的问题，目前对于有寿件备件需求的研究并不多，计算备件需求量的方法主要是基于实际平均消耗数量再乘以一个加权系数的统计方法，在GJB4355—2002[1]中该系数为1.2。该方法仅是经验上的近似方法，无法对实际保障效果进行有效评估。文献[3]提出了一种基于指数等效的有寿件备件满足率评估模型，可用于预测备件需求量，但在实际应用中该方法存在不小的误差。除此之外，其他绝大部分研究基本仅限于讨论维修/更换策略的优化问题[4-9]，而未将维修/更换策略与备件数量结合起来进行综合考虑。

本文针对上述问题，以自然寿命服从指数分布的部件为例，采用正态分布近似描述其工作寿命的思路，提出了一种确定有寿件备件需求量的方法，该方法可为保障人员合理制定有寿件的备件方案提供决策支持。

1 基于正态近似的备件需求预测模型

1.1 正态近似原理

有寿件的换件维修有两种：到寿更换和故障更换。前者是指有寿件在工作到其规定期限还未发生故障需要进行预防性维修而进行的更换。后者是指有寿件未工作到规定期限就已发生故障而进行的更换。在计算有寿件的备件需求量时，需要综合考虑这两种更换造成的备件需求。

有寿件的寿命包含自然寿命和工作寿命这两个不同的概念。对于自然寿命，它是不考虑规定的工作期限(以下简称规定期限)，该单元从开始工作一直到因故障而报废的自然寿终正寝。工作寿命考虑了规定期限的影响，它是在规定期限内，单元从开始工作一直到因故障而报废或者因到达期限而更换这一段时间，工作寿命不大于规定期限。

正常使用的电子零部件其自然寿命一般服从指数分布，如：印制电路板插件、电子部件、电阻、电容、集成电路等。本文把自然寿命服从指数分布的有寿件称之为指数型有寿件。如果仅考虑到寿更换，则备件需求预测工作极其简单。但指数型有寿件在规定期限内有可能发生故障，且发生故障的随机性较大，使其备件需求预测工作变得复杂起来。

经分析：正态分布N(μ,σ2)具有“3σ原则”[10]，即99.73%的正态变量落在(μ-3σ,μ+3σ)范围内。而对指数型有寿件的工作寿命进行观察，发现其到寿更换在现象上与正态分布在某个时段“集中”发生故障的现象有相似之处，因此本文尝试以正态分布近似描述有寿件工作寿命的分布，再利用成熟的正态型备件预测模型计算备件需求量。

1.2 备件需求预测模型

根据正态近似原理，有寿件的备件需求预测可分为以下两大步骤。

步骤1 工作寿命的正态近似

将指数型有寿件的工作寿命近似成正态分布，采用贝叶斯统计推断思想[11]，计算近似后的正态分布的参数。具体步骤如下：

1) 构造工作寿命的样本数据

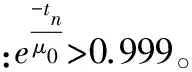
令tm为[t1,t2,…,tn]中首个不小于Tr的值，按照式(1)计算该指数单元工作寿命分别为[t1,t2,…,tm]的相对概率nP(j),j≤m，按照式(2)计算指数单元工作寿命分别为[t1,t2,…,tm]的相对次数N(j),j≤m，式(2)中的round ()函数为取整函数：

(1)

Nj= round (100*nP(j))

(2)

2) 构造正态分布候选参数矩阵

记矩阵M为正态分布候选参数矩阵，矩阵M共有K行，M(i,:)=[μiσi]。μi的取值范围为(0,Tr)，σi的取值范围为(0,0.4Tr)。μi、σi可采用遍历组合的方式产生。

3) 计算各候选参数的权重系数

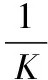
(3)

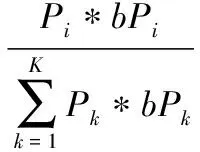
(4)

4) 在遍历[t1,t2,…,tm]结束后，得到调整完毕的各候选参数的权重系数，按式(5)计算μ、σ作为有寿件工作寿命的正态近似参数：

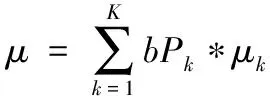
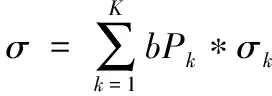
(5)

步骤2 计算备件需求量

根据正态分布的可加性：对于寿命服从N(μ,σ2)的单元，当配置S个备件时，其累积工作时间服从正态分布N((1+S)μ,(1+S)σ2)。因此，可用式(6)计算保障周期内备件数量为S时的备件保障概率Ps。

(6)

令S从0开始逐一增加，直至某值，使得Ps≥规定的保障概率指标，该S值即为所求备件需求量。

2 仿真模型

假定某单元的平均寿命为μ0，寿命T服从指数分布，记为T～exp(μ0)，其工作时间的规定期限为Tr，保障任务时间为Tw，备件数量为S。为了验证上述模型的准确性，建立如下有寿件的备件保障仿真模型，开展仿真验证。该仿真模型模拟了一次保障任务的执行情况，具体步骤如下：

1) 模拟寿命

产生1+S个随机数ti，ti服从指数分布exp(μ0)。

2) 模拟工作寿命

(7)

3) 输出保障结果Flag

(8)

Flag的物理意义为保障任务成功标志。

在多次运行该仿真模型后，对Flag进行统计，其均值simP即为保障任务成功率，由文献[12]可知，simP也是备件保障概率。

3 算例分析

算例1：某单元的平均寿命为μ0=800 h，自然寿命T服从指数分布，规定期限Tr=500 h，保障周期为Tw=2 000 h，备件数量的取值范围S=0～10。经计算，近似后的正态分布参数为μ=379.8,σ=162.1。图1所示分别为采用本文正态近似法、文献[3]的指数等效法以及仿真方法所得的备件保障概率评估曲线。从图1中可以看出：本文结果与仿真结果重合度较高，而文献[3]的结果与仿真结果差异较大。表1列出了对应的保障概率仿真结果、本文正态近似法结果、指数等效法结果和两种方法结果与仿真结果的绝对误差情况，其中正态近似法的绝对误差最大值和平均值分别为0.047和0.012，而文献[3]的指数等效法绝对误差则明显大得多，分别为0.197和0.085。

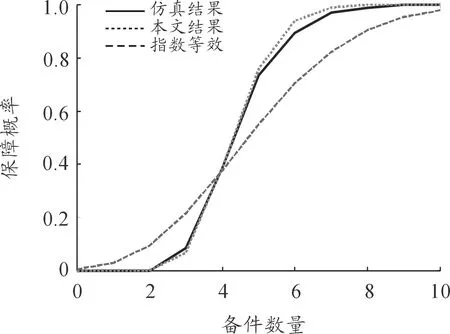
图1 不同方法的备件保障概率

当规定了具体的保障概率指标值时，可以对备件需求量进行预测。如要求保障概率分别不低于0.9、0.95时，从表1中可知本文方法和仿真方法的备件需求量预测结果均相同，分别为6、7，且二者的保障概率结果极为接近。

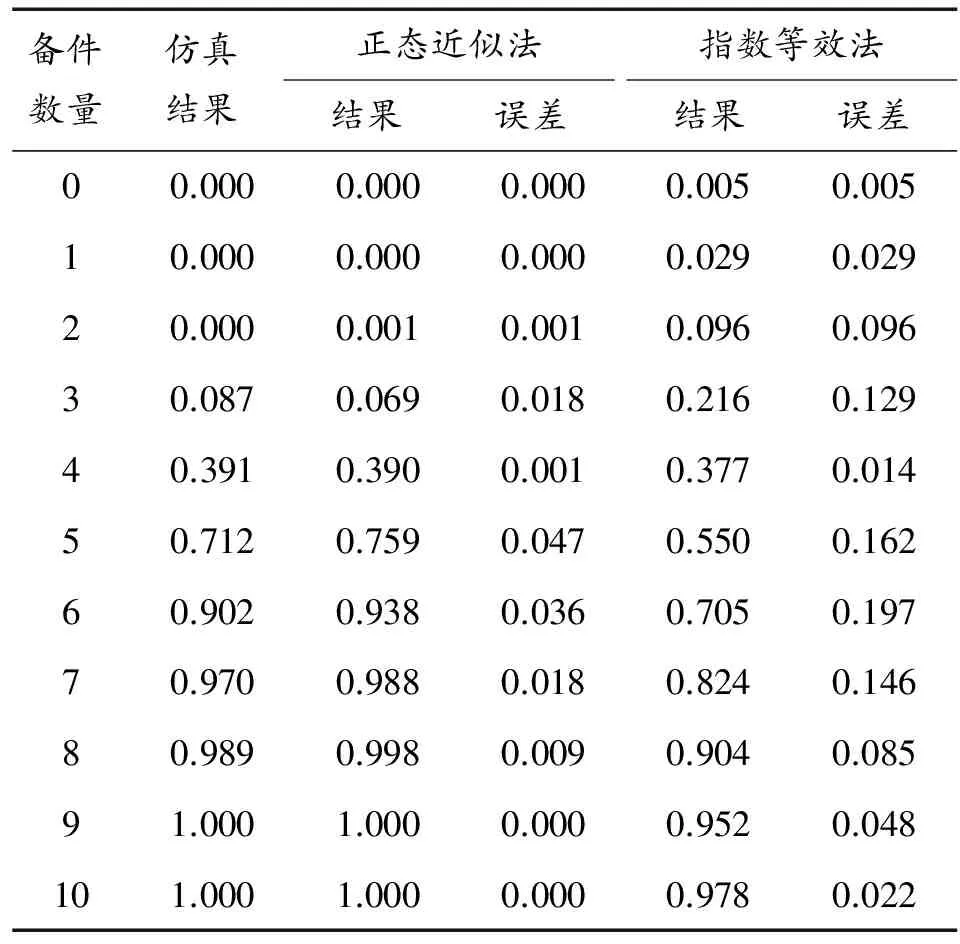
表1 不同方法的备件保障概率

算例2：某单元的平均寿命为μ0=800 h，自然寿命T服从指数分布，规定期限Tr的取值范围为200～1 200 h，保障周期Tw的取值范围为2 000～4 000 h，要求备件保障概率不低于0.85。采用本文的方法计算备件需求量，并对结果进行仿真验证。结果如表2。

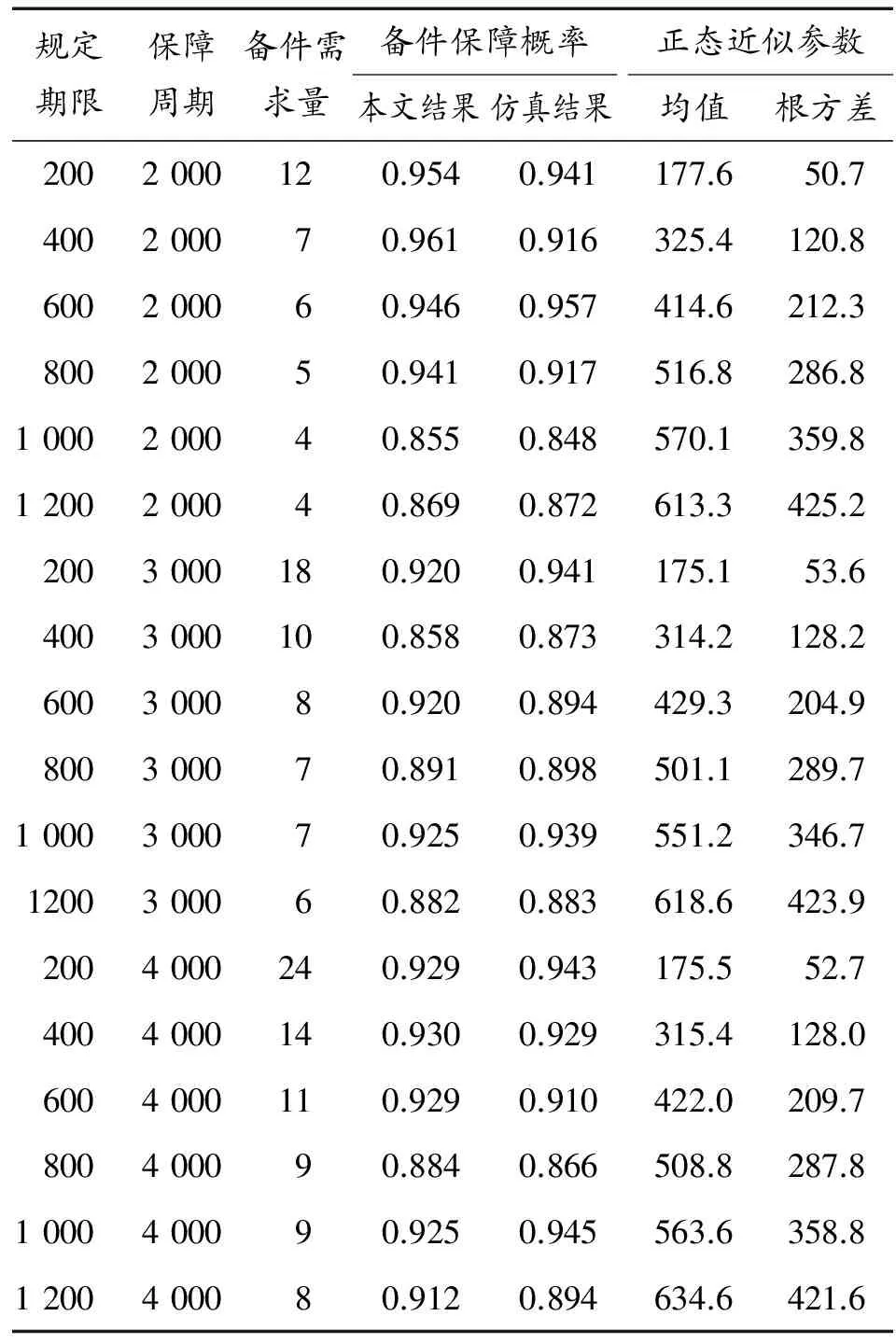
表2 算例2结果

表2中，针对各项备件需求量，本文方法计算的备件保障概率值与仿真结果相比：绝对误差最大值为0.045，绝对误差平均值仅为0.015。

大量类似算例1和算例2的仿真验证结果表明：本文方法能较为准确地计算备件需求量及备件保障概率。

4 结论

本文根据正态分布的“集中故障”与有寿件到寿更换这两种现象的相似性，以正态分布近似描述指数型有寿件的工作寿命分布，从而利用正态分布的可加性建立了该类有寿件的备件需求预测模型。仿真验证结果表明：该模型能较为准确地计算备件需求量及备件保障概率，满足工程应用要求。

[1] GJB4355—2002.备件供应规划要求[S].中国人民解放军总装备部,2003.

[2] HB7384—96.军用飞机备件配置要求[S].北京:中国航空工业总公司,1996.

[3] 金正,张志华,应新雅.舰船装备限寿备件满足率评估模型.指挥控制与仿真[J].2015(4):130-133.

[4] RUEY H Y,CHEN M Y,LI C Y.Optimal periodic replacement policy for repairable products under free-repair warranty[J].European Journal of Operational Research,2007,176:1678-1686.

[5] LI Y,MA X B,ZHAI Q Q,et al.A delay time model for a mission-based system subject to periodic and random inspection and postponed replacement[J].Reliability Engineering and System Safety,2016,150:96-104.

[6] GOLMAKANI H,MOAKEDI H.Periodic inspection optimization model for a two-component repairable system with failure interaction[J].Quality and Reliability Engineering International,2012,63(3):540-549.

[7] NAKAGAWA T,MIZUTANI S.A summary of maintenance policies for a finite interval[J].Reliability Engineering and System Safety,2009,94:89-96.

[8] SCARF P,CAVALCANTE C.Modeling quality in replacement and inspection maintenance[J].Int J Production Economics,2012,135:372-381.

[9] TAGHIPOUR S,BANJEVIC D,JARDINE A.Periodic inspection optimization model for a complex repairable system[J].Reliability Engineering and System Safety,2010,95:944-952.

[10] 峁诗松,程依明,濮晓龙.概率论与数理统计教程[M].2版.北京:高等教育出版社,2010.

[11] 韦来生,张伟平.贝叶斯分析[M].合肥：中国科学技术大学出版社,2013.

[12] 李华,邵松世,阮旻智，等.备件保障的工程实践[M].北京:科学出版社,2016.

(责任编辑唐定国)

PredictionModelofDemandsforLife-limitedSpareswithExponentialDistribution

YI Yonghua1, FU Jian2,3, WANG Chunzhi1, ZHANG Zhihua3

(1.School of Computer Science, Hubei University of Technology, Wuhan 430068, China; 2.The No. 91181stTroop of PLA, Qingdao 266405, China; 3.Department of Scientific Research, Naval University of Engineering, Wuhan 430033, China)

For the problem of uncertainty of work life distribution and difficulty in predicting demands for life-limited spares, a prediction model of demands for life-limited spares with exponential distribution is built based on approximate normal distribution. At first, work life of life-limited spares is approximate normal distribution based on Bayesian theory; Then Fill Rate model is got based on additive property of normal distribution; Finally, compared with simulation results, the example shows that this model can calculate the spares demand and its fill rate more accurately, and can meet demands of practical engineering application.

life-limited spares; spares demand; Fill Rate; approximate normal distribution

2017-07-12；

2017-07-30

易勇华(1979—)，男，副教授，主要从事装备管理研究。

后勤保障与装备管理

10.11809/scbgxb2017.11.020

本文引用格式：易勇华，傅健，王春枝，等.指数型有寿件备件需求预测模型[J].兵器装备工程学报，2017(11):89-92.

formatYI Yonghua, FU Jian, WANG Chunzhi, et al.Prediction Model of Demands for Life-limited Spares with Exponential Distribution[J].Journal of Ordnance Equipment Engineering,2017(11):89-92.

E911；TJ761.1

A

2096-2304(2017)11-0089-04