“几何画板”可以这样玩

李超贵

几何画板作为一款简单易学的数学软件，体型小巧却功能强大，可以为数学教学创设一个“做数学”的环境，开展数学实验，打造探究课堂，因而受到广大数学教师的青睐。笔者作为一名几何画板的忠实粉丝，也积累了一些使用心得，现略举一二。

一、开展数学实验，打造探究课堂

我们为了获得某种数学结论、检验某个数学猜想、解决某类实际问题时，可以利用几何画板的构造、计算、度量等功能创设“做数学”的环境，引导学生的数学思维积极参与，开展数学实验，打造探究课堂。

如对“两个三角形中有五个元素分别相等，那么这两个三角形一定全等吗？”这个问题的探究，可以设计实验探究活动———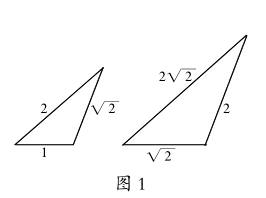

探究1.请构造出一对三角形，它们有五个元素分别相等，但这两个三角形却不全等；

探究2.这样的三角形有多少对？能否找到一般性的构造方法？

根据两个三角形全等的判定定理，这五个元素只可能是三个角、两条边，否则一定是全等的。问题的关键是我们可否构造出相应的反例。很显然，图1所示的一对三角形有五个元素分别相等，但它们不全等。

为了进一步探究这类三角形，我们可以在几何画板中搭建如下实验平台：

第一步，新建参数k，a（k>0，a>0），初始值k=1.200（注意调节参数属性，使数值精确度为千分之一，参数的键盘调节幅度为0.001），a=2.00；

第二步，计算ka，k2a，k3a，并分别画出长为a，ka，k2a，k3a的四条线段；

第三步，画线段AB=a，分别以A，B为圆心，以k2a和ka为半径画圆，记其中一个交点为C，再画线段DE=ka，分别以D，E为圆心，以k3a和k2a为半径画圆，记其中一个交点为F（如图2所示）；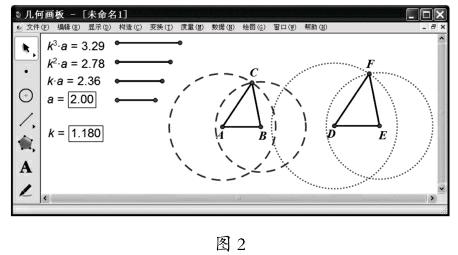

第四步，改变参数a，k的值，观察图形的变化。

通过观察实验现象，我们可以发现分别以a，ka，k2a和ka，k2a，k3a为边的两个三角形是符合条件的，它们是一对相似三角形，k是它们的相似比，用这种方法可以构造出无数多组这样的三角形。

那么，是否对于任意的参数a，k都可以构造出满足条件的一对三角形呢？通过实验我们会发现，当一对三角形构造出来后，仅改变a的值，只是改变一对三角形的大小。但当参数a固定，参数 k变化到某个范围之外时，三角形并不存在（如图3、图4所示）。

如圖7所示，先度量出DH的距离x，四边形EFKH的面积S，依次选择x，S，在“绘图”菜单中绘制点P（x，S），再选择点H，在“构造”菜单中选择“轨迹”，得到一个S关于x的函数图像，直观反映出四边形EFKH的面积S随H点位置变化的规律。分析图像特征，可以断定这是一个二次函数的图像。类似地，我们还可以研究四边形EFKH的周长、吟AGH的面积，等等。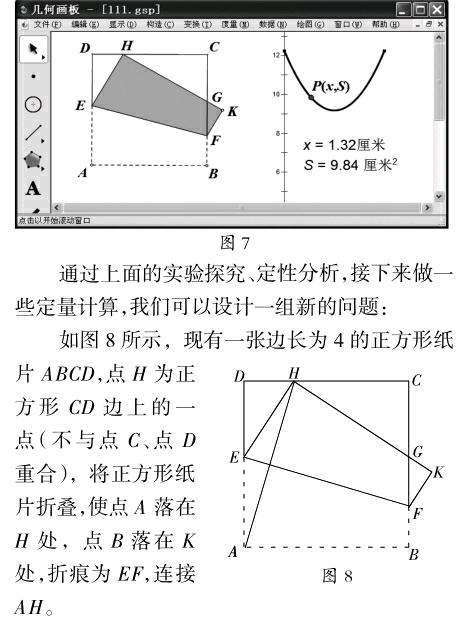

（1）求证：∠AHD=蚁AEF；

（2）求证：△CHG的周长为定值；

（3）设DH的长为x，四边形EFKH的面积为S，求出S与x的函数关系式，试问S是否存在最小值？若存在，求出这个最小值；若不存在，请说明理由。

（4）当点H移动时，设吟DEH的周长为L1，△KGF的周长为L2，判断L1+L2是否为定值，为什么？

（5）设DH的长为x，吟DEH的面积为S1，吟KGF的面积为S2，S0=S1+S2，求出S0与x的函数关系式，试问S0是否存在最大值？若存在，求出这个最大值；若不存在，请说明理由。

有了前面的实验手段作定性分析，再通过合情推理、定量计算，解决上面这组问题并不困难，读者不妨尝试一下，或许还有更多的发现。

几何画板是我们数学老师的好帮手，只要我们细心琢磨，还会玩出更多的花样。特别是我们把它当作一个数学实验的平台的时候，它的魅力会激发我们获得更多的发现与创造。

（作者单位：长沙市雨花区教育科学研究所）endprint