马圈沟河天然河道水面线推求方法探讨
(凤城市水利勘测设计院,辽宁 凤城 118100)
马圈沟河天然河道水面线推求方法探讨
赵俊卿
(凤城市水利勘测设计院,辽宁 凤城 118100)
河道水面线是河道整治设计的重要依据,直接关系到工程的型式、规模及安全运行。本文结合工程实际,运用一维能量守恒公式来探讨水面线推求的方法,以期为工程实际提供参考。
天然河道;水面线推求;能量守恒公式
马圈沟河河道治理工程位于辽宁省凤城市西南部沙里寨镇诗雅甸村马圈沟河下游,属北温带大陆性季风气候,全年平均风速2.2m/s,年均温度8.2℃,年均降水量860~1230mm,年均无霜期160d。马圈沟河是亮子河上的二级支流(图1),属山区性小河流,工程所在位置上游集雨面积2.05km2,河道全长2.22km,平均比降88.31‰。由于工程所在位置附近没有水文站,因此设计洪峰流量的计算采用《辽宁省中小河流(无资料地区)设计暴雨洪水计算方法》,得出十年一遇的洪峰流量Q10%=56.67m3/s,五年一遇洪峰流量Q20%=42.20m3/s。

图1 马圈沟河位置示意图
在河道整治过程中,修建整治建筑物、桥梁及清淤、疏浚等都会对河道水面线产生影响。河道水面线是河道整治设计的重要依据,直接关系到工程的型式、规模及安全运行。天然河道水面曲线的计算是根据河道地形地貌、河道现状横(纵)断面资料和河道糙率,推求河段在某一流量下各横断面处的水位值,根据水位值连出一条对应于该流量下的水面曲线[1]。进行河道水面线计算的方法很多,如逐段试算法、图解法以及简易计算法等。宋君[2]运用Mike11软件推求苇套河重点治理河段的水面线,确定工程规模,实现了防洪减灾和生态保护的目标。宿继成等[3]对F·F艾斯考福图解法进行改进,节省了计算工作量,提高了工作效率。胡永超[4]结合渭河干流中游段水面线计算的实际经验,提出采用二分法和弦张切法两种迭代方法相配合来解决简单的二分迭代计算时不收敛的问题。吴树煌[5]、陈彪等[6]分别对天然河道水面线中常见的问题进行研究并提出了解决方法。在研究时,软件的计算范围及应用范围广,但需要的水文资料较苛刻且对中小河流的治理工程来讲成本较高。因此在实际应用中,中小河流水面线的推求多采用数学模型进行逐段试算。本文采用一维能量守恒方程,对马圈沟河的水面线采用不同的计算条件进行推求,并分析计算结果,提出在中小河流中进行水面线推求可进行适当简化。
1 数学模型的建立与验证
研究采用水流一维能量守恒方程,方程具体形式[7-8]如下
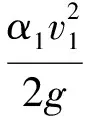
(1)
(2)
(3)
式中z——上游断面和下游断面的水面高程或水位,m;
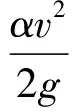
v——断面平均流速,m/s;
α——动能修正系数;
hf、hj——此河段水流的沿程水头损失和局部水头损失,m;
L——所取河段的长度,m;
R——水力半径,m;
n——糙率;
ξ——系数,河槽急剧扩大,ξ=-1.0~-0.5;河槽逐渐扩大,ξ=-0.333~-0.1。
假设河道水流为缓流,河道的控制断面设在下游,从下游往上游推算。研究采用的地形资料为实测的断面数据,设计河段全长382m,共7个断面,起始断面0+000位于河道下游,断面间距最小为56m,最大为72m,设计河道比降10.9‰。此次河道整治采用蜂巢格网基础、蜂巢格网干砌石护坡,设计坡比1∶1.5,设计过流断面为梯形。河道整治后,河道最宽处35m,最窄处27m,且从上游向下游逐渐扩大,取ζ=-0.2。马圈沟河属山区性小河流,动能修正系数α=1.5;根据附近已有工程率定,糙率n=0.033。 起始水位采用明渠均匀流公式计算,十年一遇洪峰流量Q10%=56.67m3/s时,起推水位为0.88m;五年一遇洪峰流量Q20%=42.20m3/s时,起推水位为0.75m。计算结果如图2所示。
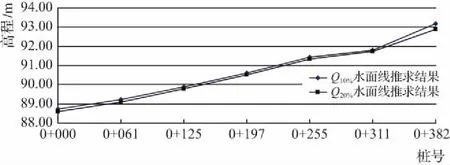
图2 Q10%、Q20%流量下水面线推求结果比较
从上图可以看出,用Q10%和Q20%推出的水面线均比较平滑,没有明显的转折或跳跃现象,两条水面线比较协调,且不同标准的水面线没有交叉[9],计算结果合理。
2 水面线的推算
由于整治后的河道基本顺直,从上游向下游逐渐扩大,整治河段平均比降10.9‰,且没有其他河流的汇入或流出,因此整治河段的局部水头损失和速度水头的变化都很小,符合一维能量守恒方程的使用条件。研究采用一维能量守恒方程,在不同的计算条件下推算马圈沟河十年一遇洪峰流量Q10%=56.67m3/s的水面线,定量分析三种计算条件的结果。
2.1 计算条件
ⓐ按一维能量守恒方程计算设计河段的水面线;ⓑ不计局部水头损失,计算设计河段的水面线;ⓒ不计速度水头损失,计算设计河段的水面线。
2.2 计算结果
三种计算条件下的计算结果如图3和下页表所示。
从图3可以看出,以下游断面作为控制断面逐段向上游推天然河道的水面线,水面线平滑,没有明显的转折或跳跃现象,从下游向上游由88.72m逐渐升高到92.8m左右,平均水面坡降10.7‰,与设计河底比降基本相等。并且前两种计算条件下的计算结果基本一致,且两者的水面线推算结果在0+255断面前与第三种计算条件下的水面线推算结果基本一致,在0+311断面前两者的计算结果略低于第三种计算条件下的推算结果,在0+382断面略高于第三种计算条件下的推算结果。
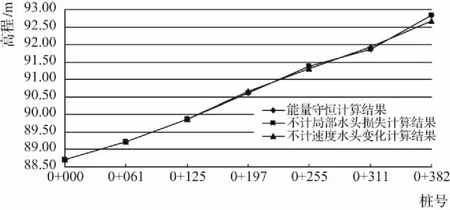
图3 三种计算条件下水面线推算结果
从下表可以看出,三种计算条件下,河道各计算河段水流的弗汝德数均为Fr<1,符合计算河段水流为缓流的假设。计算条件ⓐ、条件ⓑ计算结果基本一致,计算条件ⓒ的计算结果与条件ⓐ、条件ⓑ略有偏差,但计算结果偏差不大于6%,水位差在0.1m范围内,可以忽略不计,认为水面线推算结果一致。
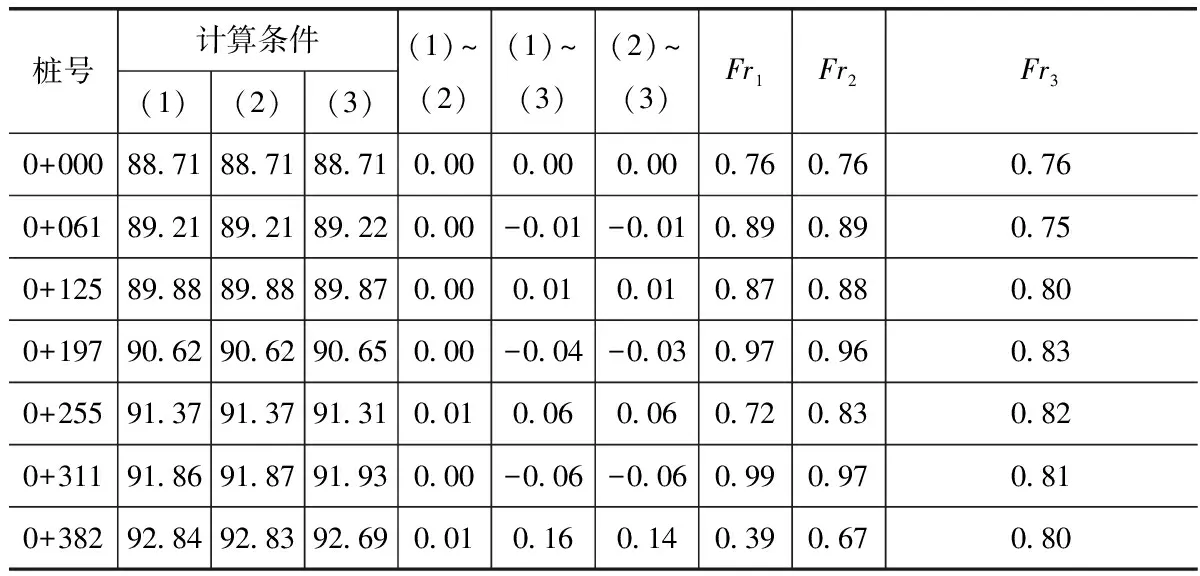
三种计算下水面线推算结果表 单位: m
2.3 计算结果分析
a. 各河段的过水断面为梯形,且沿程缓慢变大,水力坡度与河底坡度基本相等,符合明渠均匀流的的条件。
b. 各河段水流的弗汝德数均为Fr<1,各河段水流为缓流。
c. 三种计算条件下,推算水面线平滑,没有明显的转折或跳跃现象且沿程缓慢上升,符合实际情况。
d. 三种计算条件下,计算结果偏差小于6%,水位差小于0.1m,在可以接受的误差范围内,认为水面推算结果一致。
3 结 论
本文针对马圈沟河的实际情况,运用水流一维能量守恒方程推算整治河段水面线,得出主要结论如下:
a. 三种计算条件下得到的水面线均较平滑,没有明显的转折或跳跃现象且沿程缓慢上升,与实际情况相符,推算结果合理。
b. 在条件ⓐ、条件ⓑ计算条件下得到的水面线基本一致,在计算条件ⓒ下计算的水面线与前两者略有差别,但在可以接受的误差范围内,可以认为三者的计算结果一致。
c. 当断面变化不大、各断面水流流态为缓流且流速不大的情况下,在计算水面线时可以忽略速度水头的影响。
d. 在进行山区性小河流的水面线计算时,因为精度要求不高,可以不考虑速度水头,运用一维能量守恒公式快速求得水面线。
[1] 马涛. 水面线推求在中小河流治理中的应用[D]. 保定: 河北农业大学, 2013,1.
[2] 宋君. 苇套河重点河段治理规划中的水面线推求[D]. 大连: 大连理工大学, 2015.
[3] 宿继成,曲少萍,胡湘,等. 天然河道水面线计算方法的改进[J]. 黑龙江水专学报, 2006, 33(3): 167-170.
[4] 胡永超. 浅析天然河道水面线计算中的几个问题[J]. 陕西水利水电技术, 2000(1): 17-18,35.
[5] 吴树煌,华智敏,王文彬. 工程设计中天然河道水面线计算[J]. 内蒙古水利, 2008(3): 13-15.
[6] 陈彪, 陈长柏. 起推水位对河道水面线的影响分析[J]. 治淮,2009(1): 21-22.
[7] 李炜. 水力计算手册[M]. 2版. 北京: 中国水利水电出版社,2006.
[8] 郭维东,裴国霞,韩会玲. 水力学[M]. 中国水利水电出版社, 2005.
[9] 陈晓歌. 天然河道水面线计算及合理性分析[J]. 水利水电工程, 2014, 20(4): 15-16.
DiscussiononnaturalchannelflowprofilecalculationmethodofMajuangouRiver
ZHAO Junqing
(FengchengWaterConservancySurveyandDesignInstitute,Fengcheng118100,China)
Channel flow profile is an important basis for design of river channel improvement, which is directly related to engineering type, scale and safe operation. In the paper, engineering practice is combined. One-dimensional energy conservation formula is used for discussing the flow profile calculation method, thereby providing reference for engineering practice.
natural channel; flow profile calculation; energy conservation formula
10.16616/j.cnki.11- 4446/TV.2017.011.008
TV861
B
1005-4774(2017)011-0037-03

