轮式监控移动机器人的自抗扰控制
杜丽敏,雷艳敏
(长春大学 电子信息工程学院,长春 130022)
轮式监控移动机器人的自抗扰控制
杜丽敏,雷艳敏
(长春大学 电子信息工程学院,长春 130022)
将轮式监控移动机器人用于对大型养殖场动物疫病状态进行监控,是国内提出的新方案,其难点在于视频监控对机器人的平稳行走有着更高的要求,特别是工作环境比较复杂的养殖场。本文设计了基于动力学模型的自抗扰控制器,根据力矩平衡原理建立了移动机器人的动力学模型,并引入虚拟控制量将动力学模型进行解耦;再针对解耦后的方程分别建立一阶和二阶自抗扰控制器,最后在Matlab/simulink下,对所设计的控制律进行了仿真验证。结果表明,该控制系统具有较高的控制性能。
轮式移动监控机器人;动力学模型;自抗扰控制器;虚拟控制
0 引言
大规模养殖场通过移动机器人对动物疫病状态进行视频监控,可以抑制由于工作人员进入而带来的各种疾病的传播,是目前国内提出的新方案。轮式移动机器人具有自重轻、承载大、结构简单、驱动和控制相对方便、行走速度快、机动灵活、工作效率高等优点,所以,被大量应用于工业、农业、反恐防爆、家庭和空间探测等领域。机器人具有强耦合、时变和非线性的动力学特性,控制起来比较复杂。近年来,轮式移动机器人的运动控制一直都是控制领域研究的热点。有一些学者已经将非线性系统的控制方法用在了轮式移动机器人的控制当中,像滑模变结构控制[1-2],输入输出解耦控制[3],自适应控制[4-5]和反演控制[6-7]等。
为实现轮式监控移动机器人对动物疫病状态的实时监控,对机器人行走的速度平稳性提出了较高的要求。基于上述背景,本文针对易受环境干扰的轮式监控移动机器人设计了自抗扰控制器,以实现高精度的速度控制。自抗扰控制器可以对多输入多输出耦合系统进行解耦,对于不同的输入轨迹安排过渡过程,同时,把系统中的不确定项和扰动项作为扩张状态进行补偿,相对于以往的控制策略,本文给出的自抗扰控制方法更易实现机器人速度的高精度控制,完成对于现场环境的准确监视任务。本文首先建立了移动机器人的动力学模型,针对静态耦合的动力学方程引进虚拟控制量进行解耦,然后针对解耦后的数学模型设计了自抗扰控制器,最后建立了仿真,验证了所设计的控制器的有效性。
1 轮式监控移动机器人数学模型建立
独立双后轮差动驱动移动机器人通过两个后轮的不同速度来控制机器人的速度和方向。常用到两种模型:一种是运动学模型,用于解决速度和位置之间的控制问题;另一种是动力学模型,用于解决速度和输入力之间的控制问题。本文提出的是基于动力学的自抗扰控制,假设双后轮独立驱动刚性移动机器人在平面内移动,并假设绝对坐标OXY固定在平面内,下面给出动力学模型的建立过程。
根据力矩平衡原理,对于车体有:
(1)
其中,Jm为绕机器人重心的转动惯量,θ为机器人的位姿角,Fr和Fl分别为左右轮的驱动力,d为左右轮到机器人重心的距离。
根据牛顿定律有:
(2)
其中,mc为车体重量,v为机器人的线速度。
根据力矩平衡原理,对于左右车轮分别有:
(3)
其中,Jn为车轮的转动惯量,θl和θr为车轮的转角,c为粘性摩擦系数,k为增益,μl和μr为控制输入,R为车轮半径。
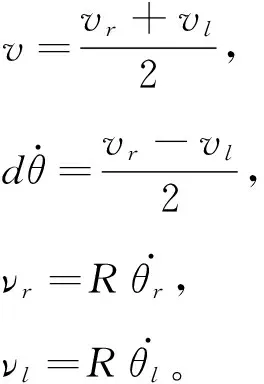
(4)
由公式(2)、(3)和(4)得:
(5)
由公式(1)、(3)和(4)得:
(6)
轮式移动机器人动力学模型由公式(5)和公式(6)组成,即:
(7)
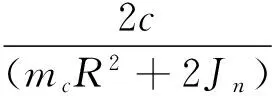


(8)
(9)
可见,每个通道的虚拟控制量与被控输出之间是单输入单输出关系,原来的系统已被解耦。
实际控制量u=[μrμl]用虚拟控制量U=[U1U2]表示为:u=B-1U
(10)
针对数学模型(8)和(9)分别设计一阶自抗扰控制器和二阶自抗扰控制器。
2 自抗扰控制器设计
自抗扰是一种可以估计补偿不确定因素的控制技术,主要由跟踪微分器、扩张状态观测器和反馈控制律三部分构成[8-11]。
2.1 跟踪微分器的设计
在这里,跟踪微分器输入为给定信号,输出两个信号,一个是为输入安排的参考信号,另一个是输入信号的近似微分信号,具体可分为非线性跟踪微分器和线性跟踪微分器。线性跟踪微分器设计简单,参数易于调节,同样具有较好的跟踪性能,因此,本文采用的是线性跟踪微分器。
设给定输入为,线性跟踪微分器的设计为:
(11)
式中,xref为给定的转速输入;x1为xref安排的过渡过程;x2为xref的微分信号;参数r决定跟踪速度,按照系统的控制能力来调节,可以解决系统超调与快速性之间的矛盾问题。
2.2 扩张状态观测器的设计
将非线性、不确定、扰动及状态方程间的动态耦合等看成一种扰动即扩张状态进行观测,被称作扩张状态观测器。扩张状态观测器有多种形式,本设计选择线性扩张状态观测器,可用带宽概念确定观测器参数,易于实现。
设计系统(8)的线性扩张状态观测器(ESO)为:
(12)

设计系统(9)的扩张状态观测器为:
(13)

2.3 反馈控制律的设计
对于系统(8),其误差信号为e11=x11-z11,取误差的线性反馈为:
U01=k1e11
(14)
系统(8)加上扰动补偿后的实际的误差反馈控制律为:
U1=k1e11-z12
(15)
对于系统(9),其误差信号为e21=x21-z21,e22=x22-z22,取误差的线性反馈为:
U02=k2e11+k3e22
(16)
系统(9)加上扰动补偿后的实际的误差反馈控制律为:
U2=k2e11+k3e22-z23
(17)
3 仿真结果与分析
在Matlab/Simulink下搭建了仿真模型,如图1所示。移动机器人结构参数a1=-0.05,a2=-0.09,b1=0.25,b2=1.67;机器人沿直线行走,线速度指令为vd=1,角度指令为θd=pi/2;控制器参数r=15,β11=200,β12=10000,β21=90,β22=2700,β23=27000,
k1=5,k2=350,k3=2。对控制输入信号μr和μl进行[-10,+10]限幅,地面阻力和扰动为[sint,sint],仿真结果如图2和图3所示。
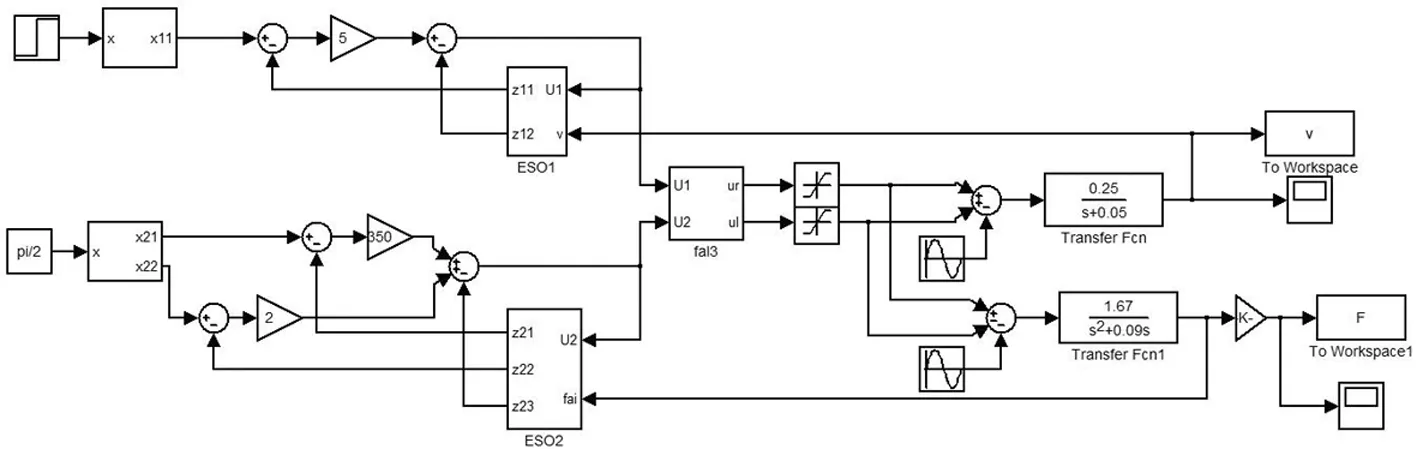
图1 移动机器人控制系统仿真框图
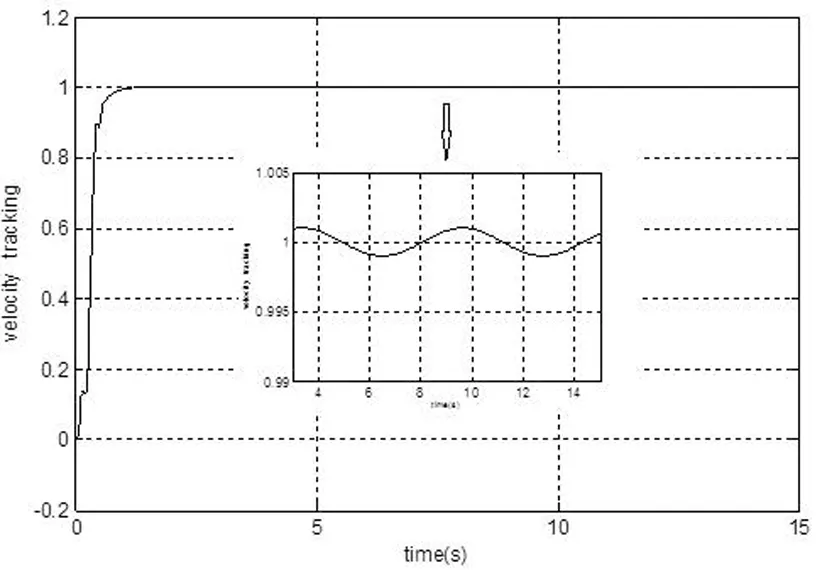
图2 线速度跟踪曲线

图3 角度跟踪曲线
图2为线速度跟踪曲线,从图中可以看出,在1.5秒左右速度就达到了稳定状态,对图形放大可以看到,即便存在干扰,稳态精度也可达到0.1%。图3为角度跟踪曲线,对图形放大可以看到,干扰下稳态精度可达到0.5%。
4 结语
本文研究了轮式移动监控机器人的轨迹跟踪问题。首先,根据力矩平衡原理建立了移动机器人的动力学模型,并引入虚拟控制量将动力学模型进行解耦。然后,针对解耦后的方程分别建立了一阶和二阶自抗扰控制器。最后,在Matlab/simulink下建立了基于动力学模型的机器人控制系统的仿真,鉴于地面阻力的影响,在仿真时加入了干扰模型,仿真结果验证了本文所设计的控制方法具有较高的速度稳定度,本文所设计的方法将具有一定的工程参考价值。
[1] YANG Min,MEIJinsong,LIAO Licheng. Design of Backstepping-based Sliding-mode Trajectory Tracking Controller for Nonholonomic Mobile Robot[J].Machine Building and Automation,2015(196):152-154.
[2] 郭一军, 俞立, 徐建明. 基于扩张状态观测器的轮式移动机器人全阶滑模控制[J]. 重庆邮电大学学报(自然科学版),2017,29(3):382-388.
[3] 池瑞楠,胡跃明,胡终须.基于解耦控制的非完整移动机器人实时轨迹跟踪[J].机器人,2001,23(3):256-260.
[4] PANG Hailong,MABaoli. Adaptive unified controller of arbitrary trajectory tracking for wheeled mobile robots with unknown parameters[J].Control Theory amp; Applications,2014(3):285-292.
[5] Veer Alakshendra,Shital S. Chiddarwar. A robust adaptive control of mecanum wheel mobile robot: simulation and experimental validation[J].IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS),2016(10):5606-5611.
[6] Walied M E Mahgoub,Ibrahim M H. Sanhoury Back stepping tracking controller for wheeled mobile robot[C]. International Conference on Communication, Control, Computing and Electronics Engineering (ICCCCEE),2017:1-5.
[7] 李小凤,黄宜庆,袁梦茹.轮式移动机器人的三维轨迹跟踪控制[J]. 安徽工程大学学报,2016(1):48-52.
[8] 阮晓刚,王旭,陈志刚.独轮机器人的建模与自抗扰控制算法[J].控制与决策,2015,30 (12):2253-2258.
[9] 阮久宏,李贻斌,荣学文,等.高速移动平台横向运动自抗扰控制[J].山东大学学报(工学版),2008,38(4):5-10.
[10] 费蓝冰,楼飞,缪国斌.欠驱动步行机器人自抗扰控制系统的设计与分析[J].江苏大学学报(自然科学版),2016,37(5):541-547.
[11] 韩京清.自抗扰控制技术[J].前沿科学, 2007(1):24-31.
责任编辑:程艳艳
ActiveDisturbanceRejectionControlofWheeledMonitoringMobileRobots
DU Limin, LEI Yanmin
(College of Electronic Information Engineering, Changchun University, Changchun 130022,China)
It is a new scheme proposed in China that wheeled monitoring mobile robots are used in large-scale farms to monitor the state of animal diseases, in which the difficult point is that video monitoring has a higher demand for the smooth walking of robots, especially in livestock farms with more complex working environment. This paper designs an active disturbance controller based on the dynamic model, establishes the dynamic model of mobile robots according to the principle of moment balance, and introduces virtual controllers to make decouple on the dynamic model, then establishes one-order and two-order auto-disturbance rejection controllers for the decoupled equation, finally, under Matlab/simulink, makes a simulation on the designed controllers. The results show that the control system has high control performance.
wheeled monitoring mobile robot; dynamics model; adaptive disturbance controller; virtual control
2017-04-08
吉林省教育厅项目(2015LY502L13)
杜丽敏(1980-),女,辽宁昌图人,讲师,博士,主要从事伺服控制方面的研究。
TP242
A
1009-3907(2017)10-0014-04

