坡地高层建筑非稳态雷暴冲击风荷载特性研究

汪之松，刘鸿，刘亚南，董志超，方智远

(1.重庆大学 土木工程学院，重庆 400045;2. 重庆大学 山地城镇建设与新技术教育部重点实验室，重庆 400045)

坡地高层建筑非稳态雷暴冲击风荷载特性研究

汪之松1,2†，刘鸿1，刘亚南1，董志超1，方智远1

(1.重庆大学 土木工程学院，重庆 400045;2. 重庆大学 山地城镇建设与新技术教育部重点实验室，重庆 400045)

目前结构风工程对于雷暴冲击风风荷载的研究多局限于稳态冲击射流模型，较少考虑风速随时间的变化以及坡地地形等因素的影响.基于冲击射流模型，引入衰减函数使得射流的入口风速更加接近真实的雷暴冲击风整个生命周期的衰变过程，并通过瞬态大涡模拟(LES)分析了坡地地形中坡顶位置处典型高层建筑的建筑风荷载特性及坡地地形雷暴冲击风场特性.结果表明，LES瞬态模拟具有较高的可靠性，非稳态冲击风场的风速波动较大，变化规律与实测的下击暴流风速曲线类似；建筑表面的风荷载具有强烈的非平稳特性，且随着风速迅速衰减；非稳态冲击风的风荷载波动大且潜在破坏能力更强；坡地地形下建筑迎风面风荷载普遍比平地小，且对建筑中上部的影响明显要大于底部，随着起坡角度的增大,建筑中上部风荷载逐渐减小.

雷暴冲击风；非稳态；坡地地形；风荷载特性；大涡模拟

由于雷暴冲击风所引起的近地面强风具有极大灾害性，从19世纪40年代起各国纷纷加大了对雷暴冲击风的研究力度.各国学者为了揭示雷暴冲击风的形成发展机理，开展了包括现场实测、解析模型、实验室物理模拟、数值模拟等多方面研究工作.

现实中的雷暴冲击风是一个风速随时间变化的非稳态过程.关于雷暴冲击风的非稳态研究，早期主要是通过实测记录的方法，Holmes和Oliver[1]在实测记录与理论分析的基础上，引入一个衰减函数乘以最大径向速度，首次提出了描述冲击风的时程曲线.Chay等[2]和Abd-Elaal等[3]基于Zhang等[4]及Wilson等[5]的数据对先前的强度衰减函数进行了改进.

Abd-Elaal等[6]在先前研究的基础上，考虑到实际风速采集时不同测点的非同步性和环境常规风场的风速对实测数据的影响，给出了一个新的速度入口强度衰减函数来模拟非稳态雷暴冲击风风场：将速度入口生命周期分成两段，第1段速度为恒定值，第2段速度突然减小到接近于0.但根据Wakimoto[7]等人研究成果，雷暴冲击风大致要经历3个或者4个阶段，简单概括为形成阶段、成熟阶段及消退阶段，实际雷暴风的消退是一个渐变的过程，因此Abd-Elaal所提出的衰减函数第2阶段与现实的雷暴冲击风消退规律存在差异.

在关注冲击风所引起的近地面强风场特征的同时，该风场作用下的建筑风荷载特性也逐渐受到风工程研究学者的重视，但针对考虑地形影响的雷暴冲击风风荷载规律讨论较为罕见.Holmes[8]对坡度为0.25的梯形山地地形进行冲击射流风洞试验，测试了单一位置处加速因子.Letchford等[9]研究了不同坡度的坡地及梯形山体地形雷暴冲击风风场特性，并测试了同一位置处的加速效应，发现加速因子与坡度成正比.Wood等[10]通过冲击射流实验，考察了坡度为0.5的坡地地形风场，得出坡顶加速因子等于1.0加上坡度值.Mason等[11-13]等对不同坡度的坡地地形的雷暴冲击风风场特性进行了研究，坡顶风速都有较明显的加速效应.

本文基于风洞试验和大涡模拟方法(LES)，在冲击射流的速度入口定义一个符合雷暴风整个生命周期的函数来模拟雷暴冲击风的全周期衰减过程，并对坡地地形影响下的高层建筑风荷载特性进行分析，得出了非稳态风场作用下的极值风荷载与平均风荷载的相关特性.

1 速度函数选择

已有研究给出的雷暴冲击风的非稳态时程如图1所示.

图1 下击暴流出流强度随时间变化的实测记录 [6]Fig.1 Normalised radial velocity versus time[6]

Holmes和Oliver[1]提出的冲击风时程曲线函数为：

Π=e(-t/T)

(1)

式中：t为雷暴冲击风达到峰值强度时的时刻；T为时间常数.

Chay等[2]和Abd-Elaal[3]等提出的改进强度衰减函数如式(2)所示.

(2)

结合Abd-Elaal[6]等的研究成果，本文同样采用两段入口风速模拟雷暴风的发展与衰减：第1段ΔtI时间内速度为恒定值；第2段Δtd时间内引入一个衰减函数来模拟冲击风的消退过程，具体表达式为：

(3)

为了便于与前期的冲击射流试验结果[14]进行对比，本文的数值计算模型采用1∶1 000的几何缩尺模型，风速比为1∶5，时间比为1∶200.为考察冲击射流持续时间的影响，数值计算时考虑入口风速函数中的ΔtI分别为0.6 s，0.9 s，1.2 s 3种情况，对应的Δtd分别为2.4 s，2.1 s，1.8 s.图2为入口风速变化曲线.

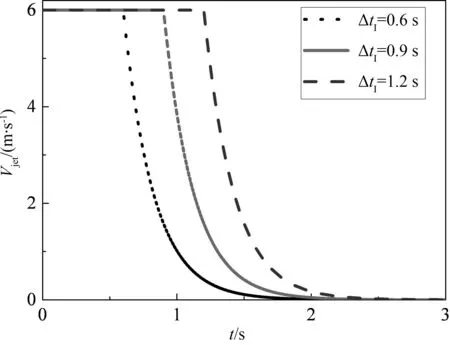
图2 入口风速变化曲线Fig.2 Inlet velocity versus time

2 冲击射流数值模拟

采用流体计算软件Fluent14.0对冲击射流模型进行数值模拟.选用大涡模型(LES)求解冲击射流非稳态射流瞬态流场.本文根据Hjelmfelt[15]对实际下击暴流尺度特征的描述取Djet=600 m，H=3Djet.计算入口采用速度入口边界条件(Velocity-inlet)，初始出流速度均为Vjet=6 m/s；LES模拟采用经典的Smagorinsky-Lilly模型，压力和速度场耦合采用SIMPLEC算法，时间步长为0.001 s，共3 000步，计算周期为3 s.另外，为了便于比较，平地与坡地冲击射流高度都采用3Djet.图3(a)和3(b)分别为平地和坡地情况下的计算域剖面及边界条件示意图.

为满足计算精度和效率，模型采用三维结构化网格，风暴中心及建筑周围为双层O型网格.对近地面和建筑表面采用增强壁面处理，近壁面最小网格高度为1×10-5m，网格总量约6.0×106，y+=0.5.为便于比较，基于雷诺平均法(RANS)和LES法进行了相同工况下稳态冲击风作用的对比计算.数值模拟工况如表1所示.

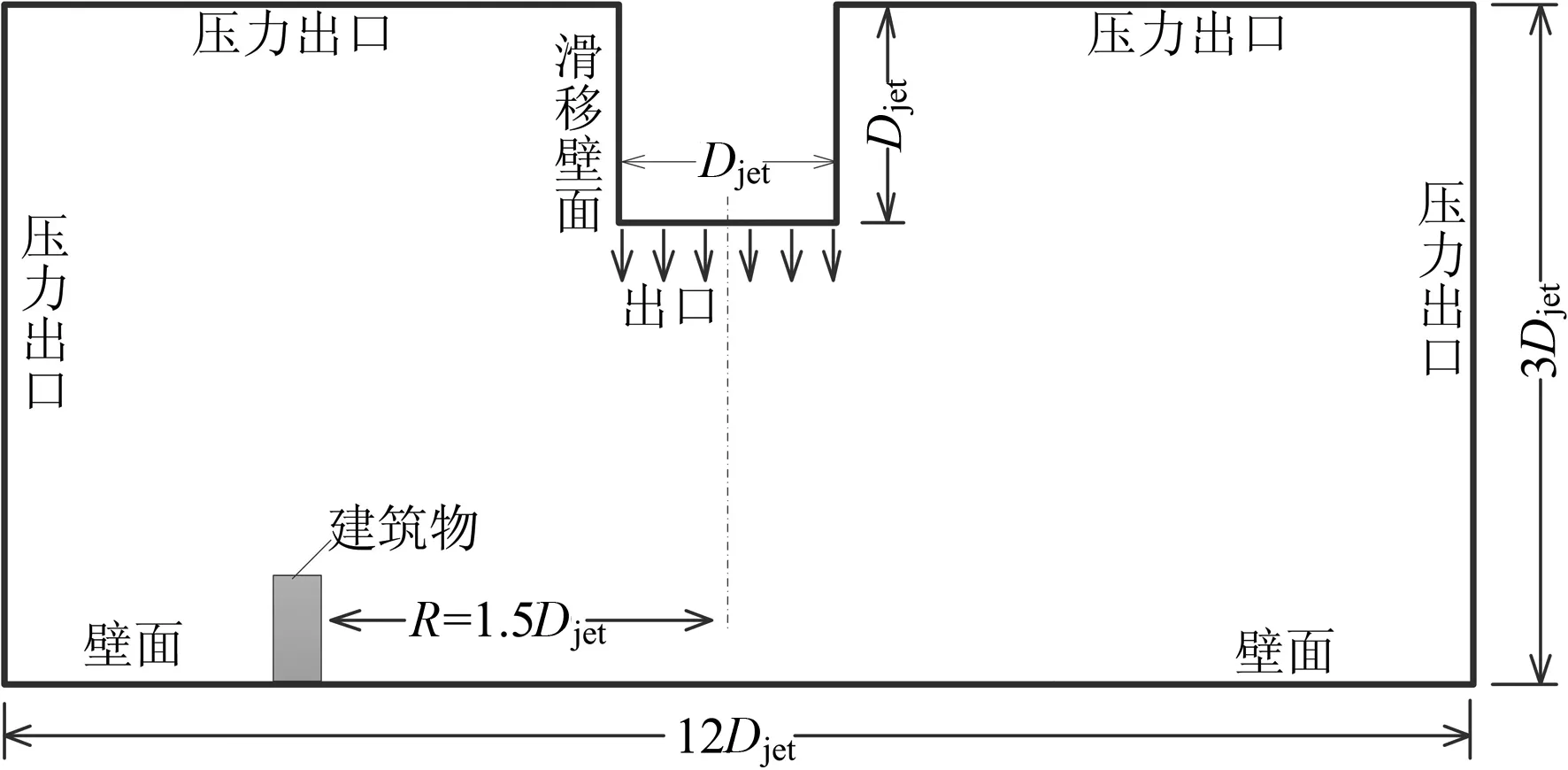
(a)平地

(b)坡地图3 数值模型计算域与边界条件示意图Fig.3 Schematic diagram of computational domain and boundary conditions

工况H/mmL/mmi/(°)平地09000i=15.0°150559.815.0i=22.5°150362.122.5i=30.0°15026030.0i=45.0°15015045.0

3 数值模拟结果与分析

3.1 非稳态雷暴冲击风风场特性

CFD数值模拟结果与现有经验模型、实测数据的水平风速竖向风剖面和径向风剖面的比较分别如图4和5所示.CFD数值模拟结果选取r=1.25Djet处的竖向风剖面，Z=0.015Djet处的径向风剖面.其中Zmax为最大水平风速对应的竖向高度，Vmax为沿径向水平风速最大值，rvmax为最大水平风速对应的径向距离.最大水平风速所在的径向位置约为1.25Djet，最大水平风速所在的高度约为0.015Djet.相关的实测数据及国外相关学者研究发现最大水平风速所在的径向位置约为1.0Djet～1.25Djet，而最大水平风速所在的高度约为0.005Djet～0.025Djet，与本文计算结果基本一致.

图4 CFD数值模拟与各模型竖直风剖面比较Fig.4 Comparison of vertical wind profile of CFD numerical simulation and analytical models

图5 CFD数值模拟与各模型径向风剖面比较Fig.5 Comparison of radial wind profile of CFD numerical simulation and analytical models

图6给出了3种ΔtI下最大水平风速的时程曲线对比图.

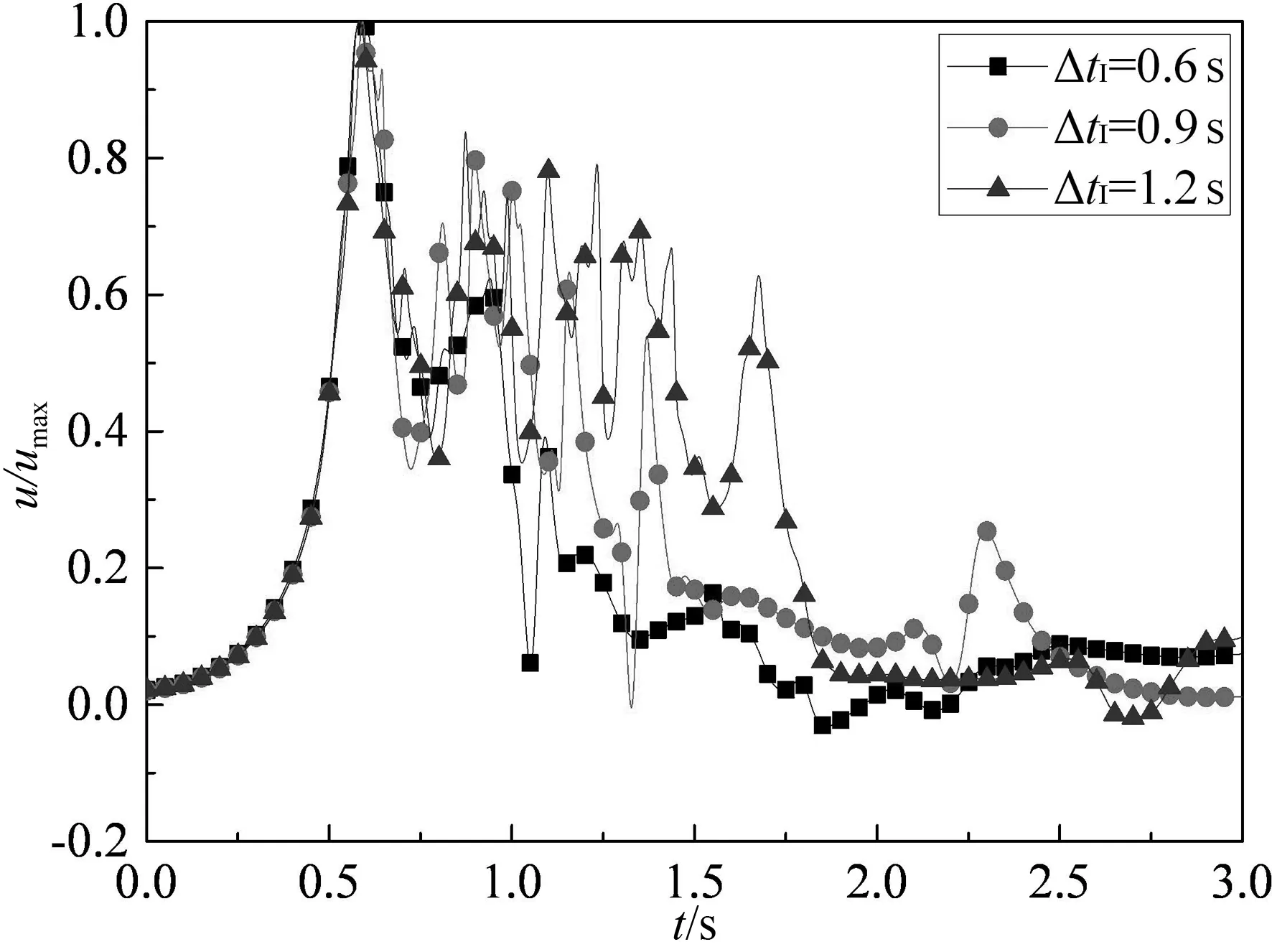
图6 3种不同周期下最大水平风速的时程曲线Fig.6 Normalised temporal profiles of the radial speed at location of maximum speed for three different ages

从图6可以看出,3种情况下的测点(径向1.25Djet，高度为0.015Djet)均在0.6 s时刻达到了最大值，此时主漩涡经过测点位置，使得径向出流强度达到了最强；当入口风速开始衰减时，测点风速并非迅速衰减，而是继续保持一段相对稳定后才逐渐衰减；随着入口风速稳定段ΔtI的增加，测点风速衰减段较大风速持续的时间也逐渐增加.

图7和图8分别给出了平地与坡地情况下，1.5Djet径向位置不同高度处的水平风速时程曲线和竖向风速时程曲线，反映了速度强度沿高度方向的变化趋势.水平风速随着高度的增加先增加到最大值(Z=0.015Djet)，然后逐渐减小；竖向风速随着高度的增加持续增加；坡地地形对坡顶处测点的风速时程变化趋势影响不大，坡地对坡顶处的竖向风速影响较大，坡地坡角越大，坡顶测点的竖向风速越大.

(a)平地 (b) i=15°

(c) i=22.5° (d) i=30°图7 1.5Djet径向位置不同高度处的水平风速时程曲线Fig.7 Normalised temporal profiles of the radial speed at r/D=1.5 for different heights(ΔtI=0.9 s)

(a)平地 (b)i=15°

(c) i=22.5° (d) i=30°图8 1.5Djet径向位置不同高度处的竖向风速时程曲线Fig.8 Normalised temporal profiles of the vertical speed at r/D=1.5 for different heights(ΔtI=0.9 s)

3.2 非稳态雷暴冲击风风荷载特性

3.2.1 迎风面风压瞬时特性

限于篇幅，仅给出在ΔtI=0.9 s，坡角i=30°情况下风速云图及建筑迎风面风压系数(如图9所示).从图9中可以看出，在t=0.45 s时，喷口出流速度相对稳定，来流风到达建筑物表面，由于建筑阻挡,在坡顶处建筑底部有一气流停滞点，建筑迎风面风压呈层状分布且下大上小,但总体值较小(见图9(a))；在t=0.90 s时，喷口出流稳定，来流风流过建筑，大约在建筑1/4高度处来流风受建筑阻挠产生分离，一部分气流向下运动形成旋涡，另一部分沿建筑表面上升并越过建筑表面，受这一影响建筑表面风压系数在1/4高度位置达到最大值，而两端较小部分边沿处出现负压(见图9(b))；在1.35 s之后，喷口风速急剧减少，建筑附近来流风风速急剧减少，建筑表面风压系数急剧减少(见图9(c)和(d)).

(a)t=0.45 s

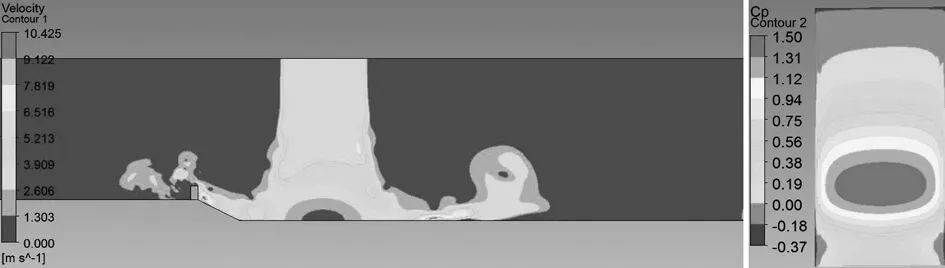
(b)t=0.90 s

(c)t=1.35 s

(d)t=2.25 s图9 各时刻风速云图及建筑迎风面风压系数Fig.9 The time wind speed and cloud building windward pressure coefficient at different time

3.2.2 风荷载的瞬时特性

迎风面测点布置及层划分如图10所示.对数值模拟得到测点的时程风压进行了处理，图11给出了平地1.5Djet工况迎风面中线测点的风压系数时程曲线.由图11可以看出，建筑模型中下部区域测点的极值风压较大，而上部区域测点的极值风压相对较小，不足下部测点的一半，这与雷暴冲击风在近地面区域风场特性相关；非稳态雷暴冲击风作用下建筑模型迎风面测点的极值风压远远大于LES瞬态模拟和RANS稳态模拟风压的时均值，极值风压约为时均风压的2.2～2.5倍.

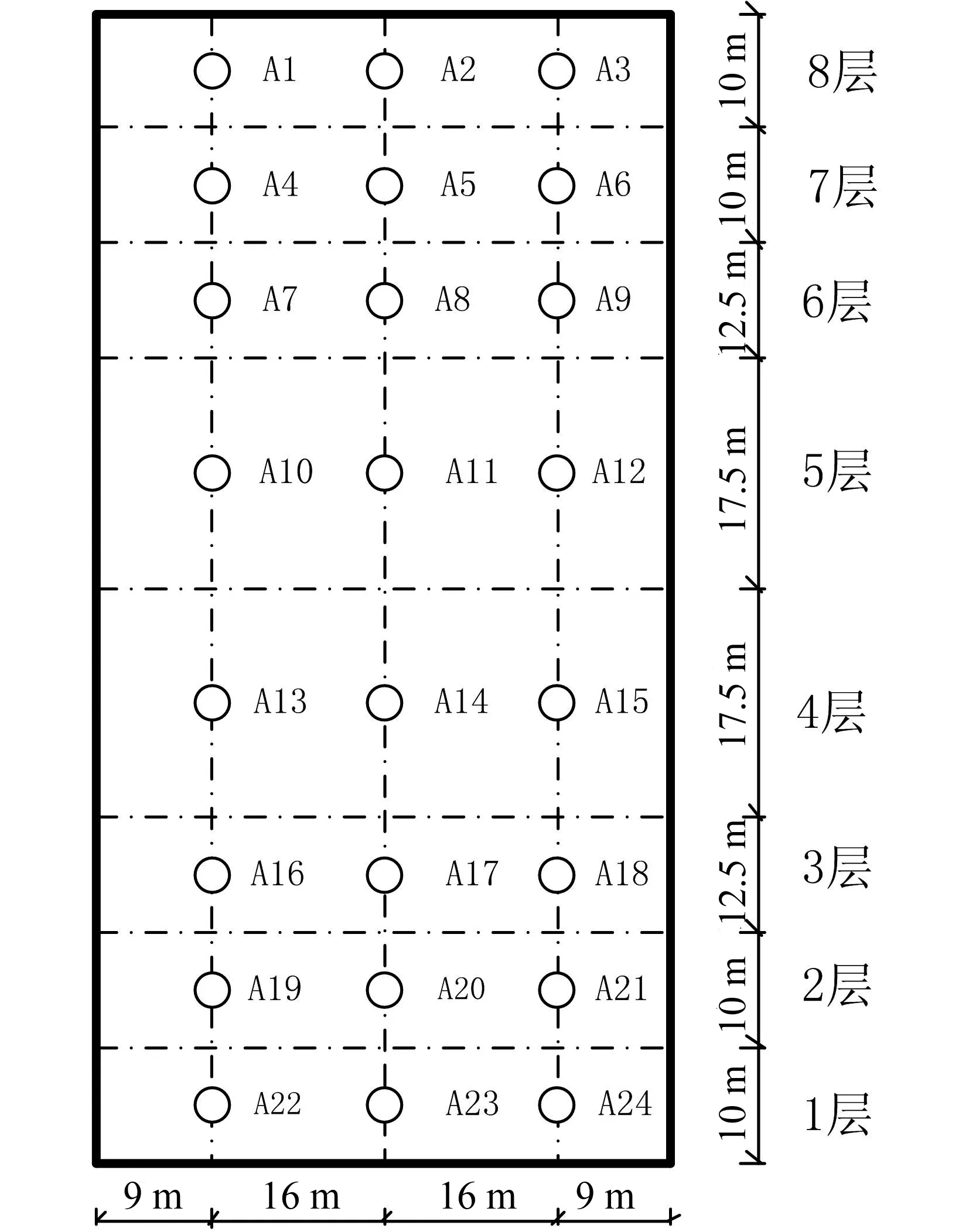
图10 建筑模型压力测点层划分Fig.10 Layer division of measuring points

图12给出了平地及不同坡地工况迎风面中线各高度测点的风压系数时程曲线.近地面处测点的风压较大，随着高度的增加，测点的风压逐渐减小.坡地地形对迎风面测点的风压时程变化趋势影响不大，相比平地而言，坡地测点的风压有所减小.

实际工程中更关注的是建筑各层的风荷载，对非稳态数值模拟的压力测点进行层划分，图13和图14分别给出了各层的层阻力系数时程曲线及地形对各层阻力系数时程曲线的影响.从图中可以看出，雷暴风作用下高层建筑的阻力主要体现在建筑模型中下部区域，这与雷暴风水平风速的竖向风剖面相一致.坡地对2，3，4层的阻力系数影响较小，而对7层的阻力影响较大，当坡度较大时，层阻力有减小的趋势.

为了探究雷暴风作用下高层建筑的极值风荷载与平均风荷载的大小关系，图15和图16分别给出了平地1.5Djet工况和坡地i=30°工况非稳态层阻力曲线与风洞试验、RANS稳态模拟及LES瞬态模拟得到的时均层阻力系数对比图.从图中可以看出，风洞试验、RANS稳态模拟和LES瞬态模拟得到的时均层阻力系数具有较高的吻合度，3种方法相互验证了此研究结果的可靠性.建筑模型中下部区域的层阻力较大，而中上部区域的层阻力相对较小，平地地形7层的极值阻力约为2层的极值阻力的70%，i=30°坡地地形7层的极值阻力约为2层的极值阻力的43%，这与雷暴冲击风在近地面区域风场特性相关；与稳态风荷载均值相比，非稳态时变雷暴风波动较大，同时非稳态冲击风效应也具有潜在巨大的破坏能力，顺风向的极值阻力为稳态均值风荷载的2.2～2.5倍.

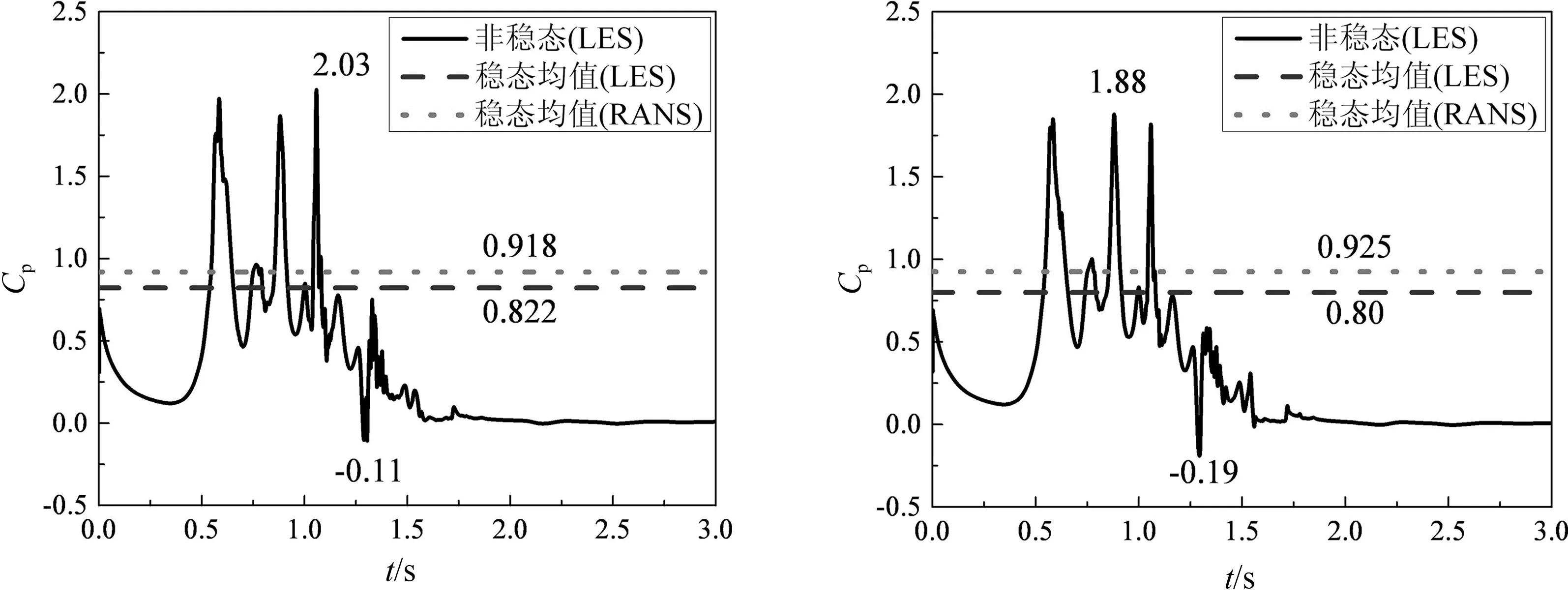
(a) 测点A23(Z=0.05H) (b) 测点A20 (Z=0.15H)

(c) 测点A17(Z=0.25H) (d) 测点A2(Z=0.95H)图11 迎风面中线测点的风压系数时程曲线Fig.11 Pressure coefficient time-history of windward center-line points(ΔtI=0.9 s)

(a) 测点A23 (b) 测点A20

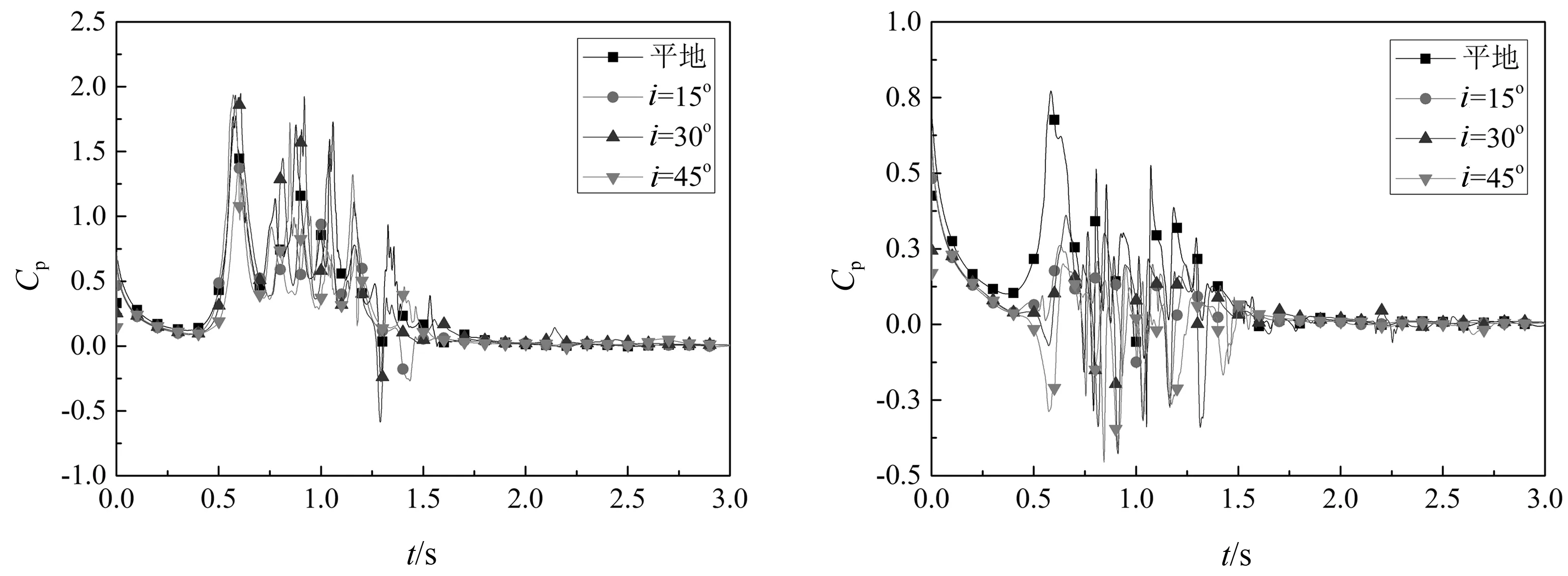
(c) 测点A17 (d) 测点A2图12 不同工况迎风面中线各高度测点的风压系数时程曲线Fig.12 Pressure coefficient time-history of windward center-line points at various height in different cases(ΔtI=0.9 s)

(a)平地(b)i=30°图13 不同工况各层阻力系数时程曲线Fig.13 Dragcoefficienttime-historyofeverylayerindifferentcases(ΔtI=0.9s)

(a)1层(Z=0.1H～0.2H)(b)3层(Z=0.2H～0.325H)(c)4层(Z=0.325H～0.5H)(d)7层(Z=0.8H～0.9H)图14 地形对各层阻力系数时程曲线的影响Fig.14 Effectoftopographyondragcoefficienttime-historyofeverylayer(ΔtI=0.9s)

(a)2层(Z=0.1H～0.2H)

(b)3层 (Z=0.2H～0.325H)

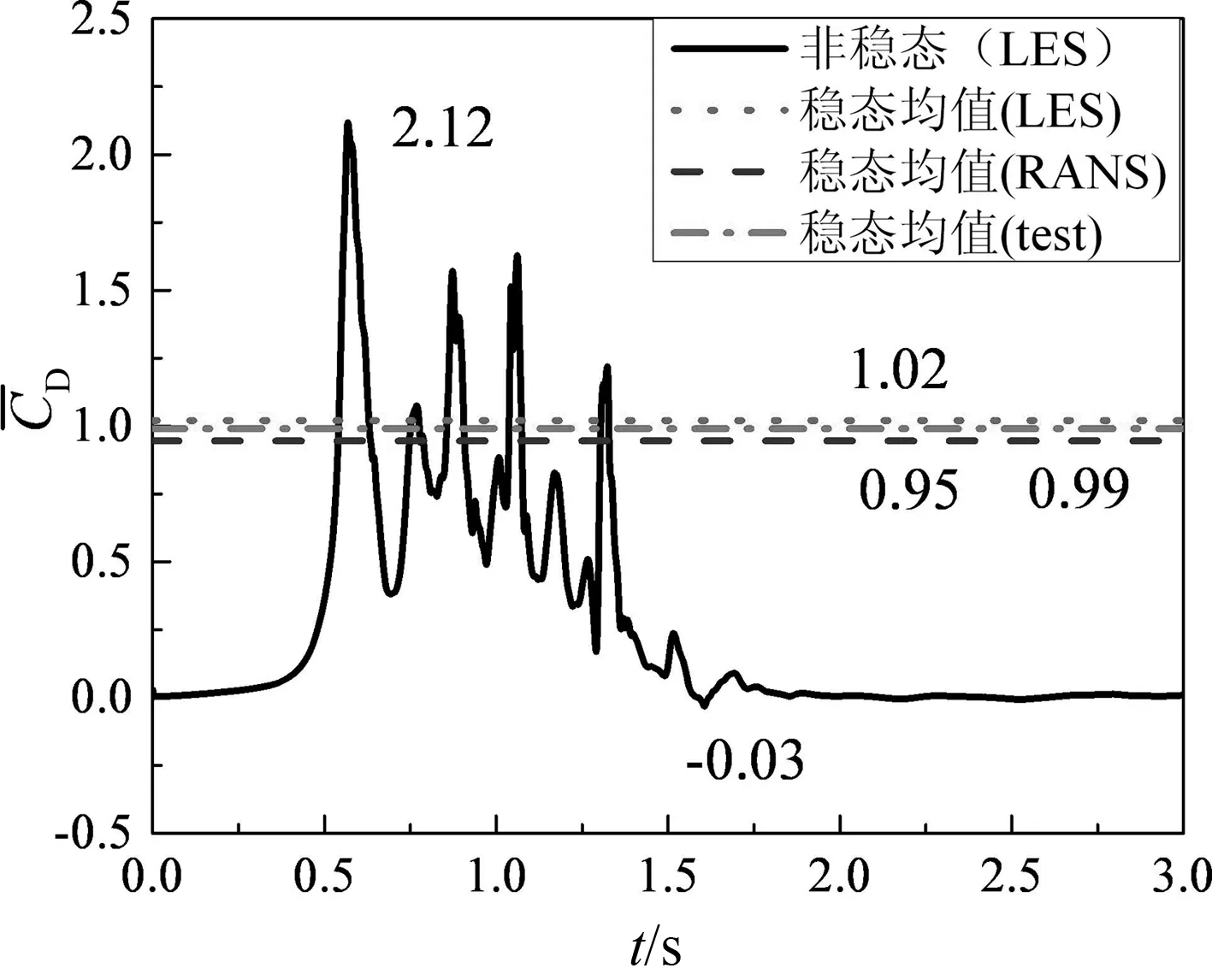
(c)4层(Z=0.325H～0.5H)

(d)7层(Z=0.8H～0.9H)图15 各层阻力系数时程曲线与时均值的对比图(平地工况1.5Djet)Fig.15 Comparisons of time-history curve and mean value of drag coefficient of each layer(1.5Djet)

(a)2层(Z=0.1H～0.2H)

(b)3层 (Z=0.2H～0.325H)

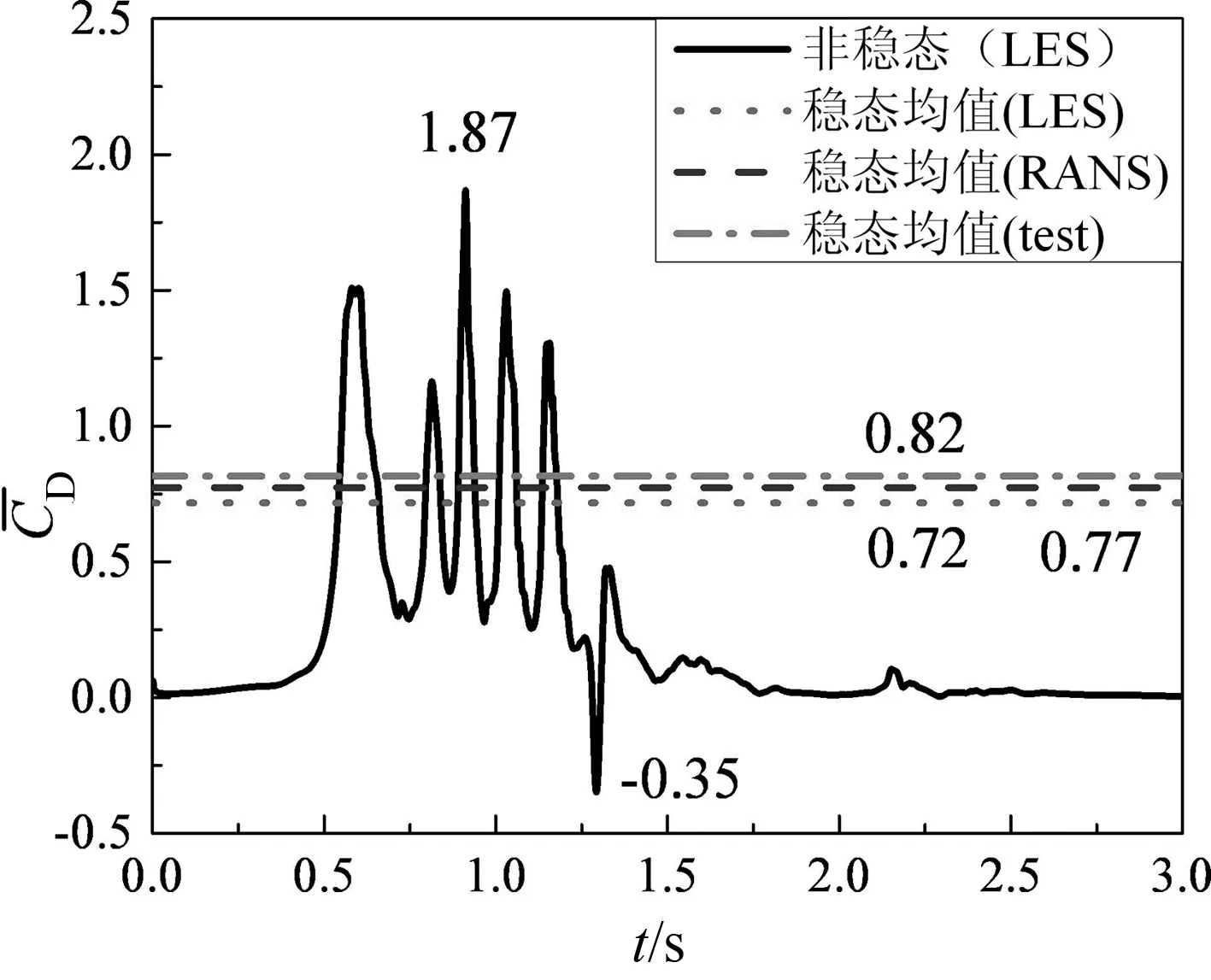
(c)4层(Z=0.325H～0.5H)

(d)7层(Z=0.8H～0.9H)图16 各层阻力系数时程曲线与时均值的对比图(坡地工况i=30°)Fig.16 Comparisons of time-history curve and mea value of drag coefficient of each layer(i=30°)

图17分别给出了坡地i=15o，i=45o时，ΔtI=0.6 s，ΔtI=0.9 s，ΔtI=1.2 s 3种工况下建筑迎风面中线处的风压系数对比图，图18列出了不同工况不同层的风压系数时程曲线.从图17中可以看出，不同生命周期雷暴风的风压系数极值没有明显区别，曲线走势相同，但是生命周期越长建筑表面风压持续时间也越长，这与人们主观感受的作用时间越长破坏越大相契合.而图18所反映的建筑底部跟上部在不同工况下风压系数曲线变化趋势同样高度相似，这一方面印证了模拟的准确性，另一方面也反映了雷暴风持续越久对建筑破坏越大这一结论是正确的.

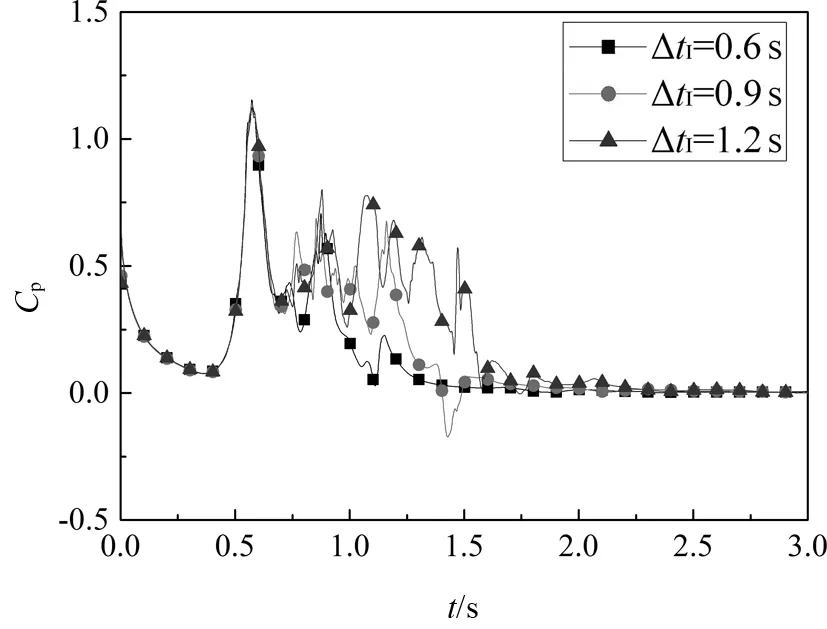
(a) i=15°

(b) i=45°图17 不同生命周期不同坡角建筑迎风面中线风压系数时程曲线Fig.17 Pressure coefficient time-history curve of windward center-line points of different slope angles in different life cycles

(a)2层(Z=0.1H～0.2H)

(b)7层(Z=0.8H～0.9H)图18 不同工况不同层风压系数时程曲线Fig.18 Pressure coefficient time-history of different layer in different cases

4 结 论

本文引入一个符合雷暴冲击风生命周期演化过程的数学模型来模拟接近真实情况的下击暴流冲击风衰减过程，并对该非稳态瞬时风场作用下的建筑物风荷载特性进行了数值模拟研究，对比了平地及不同坡角情况下坡顶位置处典型高层建筑的风压及层风荷载特性，主要结论有：

1)与稳态冲击射流风场相比，非稳态冲击风场的风速波动较大，变化规律与实测的下击暴流风速曲线类似，雷暴冲击风近地面风场其水平风速和竖向风速大体上都是在短时间内迅速达到最大值，然后保持一定值波动后迅速衰减为零.

2)非稳态冲击风作用下的LES瞬态模拟结果表明，建筑表面的风荷载具有强烈的非平稳特性，在入口风速为恒定值阶段，随着时间推移建筑表面风荷载逐渐达到最大值，然后随着风速衰减建筑表面风荷载迅速衰减；且雷暴风对于建筑中部影响明显大于建筑上部跟底部.

3)LES瞬态模拟与之前的风洞试验得到的时均层阻力系数吻合较好，验证了本文采用的LES数值模拟具有较高的可靠性.非稳态冲击风的风荷载波动大且潜在破坏能力更强，在建筑物顺风向，非稳态冲击风的极值阻力可达稳态时的2.2～2.5倍.

4)对于不同坡度情况下的坡地顶部高层雷暴冲击风荷载的分析表明，起坡角度对于建筑物的顺风向风荷载有一定的影响，坡地地形下建筑迎风面风荷载普遍较平地小，且对建筑中上部的影响明显要大于底部，随着起坡角度的增大，建筑中上部风荷载逐渐减小.

[1] HOLMES J D,OLIVER S E. An empirical model of a downburst[J]. Engineering Structures,2000,22(9):1167-1172.

[2] CHAY M T,ALBERMANI F,WILSON R. Numerical and analytical simulation of downburst wind loads[J]. Engineering Structures,2006,28(2): 240-254.

[3] ABD-ELAAL E S, MILLS J E, MA X. A coupled parametric-CFD study for determining ages of downbursts through investigation of different field parameters[J]. Journal of Wind Engineering & Industrial Aerodynamics, 2013, 123:30-42.

[4] ZHANG Y,SARKAR P,HU H. An experimental study on wind loads acting on a high-rise building model induced by microburst-like winds[J]. Journal of Fluids and Structures,2014,50:547-564.

[5] WILSON J W,ROBERTS R D,KESSINGER C,etal. Microburst wind structure and evaluation of Doppler radar for airport wind shear detection[J]. Journal of Climate and Applied Meteorology，1984,23(6):898-915.

[6] ABD-ELAAL E,MILLS J E,MA X. Empirical models for predicting unsteady-state downburst wind speeds [J]. Journal of Wind Engineering and Industrial Aerodynamics,2014,129:49-63.

[7] WAKIMOTO R M. The life cycle of thunderstorm gust fronts as viewed with Doppler Radar and rawinsonde data[J]. Monthly Weather Review,1982,110(8):1060-1082.

[8] HOLMES J D. Physical modelling of thunderstorm downdrafts by wind-tunnel jet[C]//Proceedings of the Second AWES Workshop. Monash:Monash University,1992:29-32.

[9] LETCHFORD C W,ILLIDGE G.Topographic effects in simulated thunderstorm downdrafts by wind tunnel jet[C]//Proceedings of the Seventh AWES Workshop.Auckland,1998:25-28.

[10] WOOD G S,KWOK K C S,MOTTERAM N A,etal.Physical and numerical modeling of thunderstorm downbursts [J].Journal of Wind Engineering and Industrial Aerodynamics,2001,89:535-552.

[11] MASON M S,WOOD G S,FLETCHER D F.Numerical simulation of downburst winds [J]. Journal of Wind Engineering and Industrial Aerodynamics,2009,97(11/12): 523-539.

[12] MASON M S. Numerical investigation of the influence of topography on simulated downburst windfields[J]. Journal of Wind Engineering and Industrial Aerodynamics,2010,98:21-33.

[13] MASON M S,FLETCHER D F,WOOD G S.Numerical simulation of idealized three-dimensional downburst wind fields [J].Engineering Structures,2010,32: 3558-3570.

[14] 邹鑫，汪之松，李正良.稳态冲击风作用下高层建筑风荷载特性试验研究[J].湖南大学学报,自然科学版.2016,43(1):29-36.

ZOU Xin,WANG Zhisong,LI Zhengliang. Experimental study on the wind load characteristics of high-rise building in stationary downbursts[J].Journal of Hunan University: Natural Sciences,2016,43(1):29-36. (In Chinese)

[15] HJELMFELT M R. Structure and life cycle of microburst outflows observed in colorado[J]. Journal of Applied Meteorol-ogy,1988,27(8):900-927.

Analysis on Wind Load Characteristics of High-rise Buildingsunder Unsteady-state Downburst over Slope Topography

WANG Zhisong1,2†,LIU HONG1,LIU Yanan1,DONG Zhichao1,FANG Zhiyuan1

(1.School of Civil Engineering,Chongqing University,Chongqing 400045,China;2. Key Laboratory of New Technology for Construction of Cities in Mountain Area,Ministry of Education,Chongqing University,Chongqing 400045,China )

The existing researches for wind load characteristics of the downburst mainly concentrated on stationary impinging jet model，but rare investigation was for time-varying characteristics and the impact of mountain terrain. In this paper，based on the impinging jet model，the decay function was brought in to make the inlet wind velocity more close to the decay process of the whole life cycle of the thunderstorm，and the wind load characteristics of typical high-rise buildings on the top of the slopes and the characteristics of the thunderstorms on the slope landforms were analyzed by transient large eddy simulation (LES). The results show that the transient simulation of LES is more reliable，the wind speed fluctuation of the unsteady shock wind field is larger，and the variation law is similar to the measured wind speed curve. The unsteady wind load shows strong unsteady characteristics，greater fluctuations and rapid attenuation with wind speed. The wind load fluctuation of unsteady shock wind is wide and has strong potential to damage，the wind load on the sloping terrain is generally smaller than that of the flat ground，and the influence of the slope terrain on the upper part of the building is obviously higher than that of the bottom. With the enlarging of slope angle，the upper wind load gradually decreases.

downburst；unsteady state；slope terrain；wind load characteristics；Large Eddy Simulation (LES)

TU973.213

A

1674-2974(2017)11-0088-11

10.16339/j.cnki.hdxbzkb.2017.11.011

2016-10-09

国家自然科学基金资助项目(51208537),National Natural Science Foundation of China(51208537)

汪之松(1980— )，男，安徽舒城人，重庆大学副教授，博士

†通讯联系人，E-mail：wangzhisong@cqu.edu.cn