核岛结构双钢板混凝土组合剪力墙抗侧刚度

李小军，李晓虎 ，张慧颖

(1. 北京工业大学 建筑工程学院，北京 100124；2. 中国地震局 地球物理研究所，北京 100081)

核岛结构双钢板混凝土组合剪力墙抗侧刚度

李小军1,2，李晓虎1†，张慧颖1

(1. 北京工业大学 建筑工程学院，北京 100124；2. 中国地震局 地球物理研究所，北京 100081)

为研究核岛屏蔽厂房结构在地震作用下的抗侧力能力，对9个1∶5缩尺比的双钢板混凝土组合剪力墙试件进行了低周往复拟静力试验，分析研究了栓钉间距、钢板厚度和加劲肋的设置等因素对剪力墙试件初始抗侧刚度的影响.研究结果表明：栓钉间距对剪力墙试件初始刚度的影响不明显，剪力墙初始抗侧刚度随着钢板厚度的增大和加劲肋的设置而有所提高.对试件进行理论假设和简化处理，利用单位荷载法推导出双钢板混凝土组合剪力墙试件初始抗侧刚度的计算公式，通过比较发现计算值和试验值吻合较好.研究了剪力墙试件在往复加载过程中抗侧刚度的变化过程，发现不同阶段的抗侧刚度在变化幅度上有差别.

双钢板混凝土剪力墙；低周往复试验；初始抗侧刚度；抗侧刚度

由于核电的安全、高效和清洁的优点以及目前全球资源枯竭的现状，中国大陆对于核电站的开发进入了积极发展阶段.而核电站一旦发生事故，对周边环境和国家经济都会带来严重的影响.2011年3月在日本发生的9.0级地震导致福岛核电站事故，其造成的灾害之大给我们敲响了警钟，因此对核电站外部保护结构屏蔽厂房的研究至关重要.目前我国部分拟建和在建的核电站中，屏蔽厂房采用的是双钢板混凝土组合剪力墙结构[1].资料显示[2-5]，钢板混凝土剪力墙结构目前主要应用于民用高层建筑和海洋当中，对应用在核电工程的钢板混凝土剪力墙结构的研究还处于初级阶段.

1 研究背景

CAP1400核电站是我国拥有自主知识产权和独立出口权的第三代先进核电技术.资料显示AP1000核电站的屏蔽厂房设计在辐射防护方面还存在一些缺陷，因此在CAP1400核电站设计中屏蔽厂房的安全性能成为关键.双钢板混凝土组合剪力墙是我国自主研发的应用于CAP1400核电站屏蔽厂房的结构体系[6].

目前，已有国内外学者对钢板混凝土剪力墙抗震性能等方面进行了有限元分析和试验研究.Hossain等[7]对钢板混凝土剪力墙的缩尺模型进行了面内抗剪强度试验，研究了钢板混凝土在水平荷载作用下强度、刚度的变化情况以及试件的破坏模式等，建立有限元分析模型并与试验结果进行相互验证.Ozaki等[8]通过对9个钢板混凝土剪力墙试件进行的两组低周往复荷载试验和有限元分析研究了竖向荷载和开口对钢板混凝土剪力墙抗震性能的影响，并得出不同剪切模量的计算公式.司波等[9]分析研究了钢板厚度、高厚比等因素对双钢板剪力墙抗侧刚度的影响，并且利用单位荷载法推导出了双钢板剪力墙初始抗侧刚度的计算公式，与试验结果比较吻合.罗永峰等[10]在试验研究的基础上，采用数值分析的方法分析了双层钢板混凝土组合剪力墙结构的受力特点；通过对比试验和数值分析结果，分析了轴压比、高宽比、宽厚比等因素对剪力墙滞回性能的影响，得出高宽比和宽厚比是影响初始刚度的主要因素.程春兰等[11]对16个带约束拉杆的双钢板混凝土组合剪力墙进行了往复加载试验，并结合Opensees程序对剪力墙试件的数值模拟，研究了组合剪力墙的抗震性能；研究结果表明：高宽比、轴压比和约束拉杆间距都对剪力墙的抗震性能有显著影响.对于核电站屏蔽厂房双钢板混凝土剪力墙抗震性能的研究目前取得了一些新的进展.但对于试件的设计没有考虑边界约束，在进行理论分析时，忽略了混凝土对抗侧刚度的影响.对于双钢板混凝土组合剪力墙抗侧刚度的研究，需要综合考虑这些因素进行分析计算.张有佳等[12]通过对6个双钢板混凝土剪力墙试件进行低周往复荷载试验，分析了剪力墙墙体构件的破坏模式和破坏特征，并且分析了栓钉间距、加劲肋等因素对墙体整体刚度、承载能力和延性的影响.熊峰等[13]对3个1∶4的核电站双钢板混凝土剪力墙试件进行了低周往复加载抗剪试验研究，分析了试件的破坏特征、承载力以及耗能情况，通过有限元数值模拟研究了混凝土强度、钢板厚度、轴压力等因素对抗剪强度的影响，并得出了抗剪强度的计算公式.从文献[12]和文献[13]的试验结果发现，试验因为试件的钢筋混凝土基础在往复荷载作用下发生破碎而终止，对此需要对试件的基础进行加固设计.

目前，对于核电站双钢板混凝土组合剪力墙抗侧刚度的研究较少，然而墙体的抗侧刚度是核电站结构的抗震性能的一个关键性指标，合理地分析和设计双钢板混凝土组合剪力墙抗侧刚度对保证核电站结构地震安全至关重要.本文设计了9个缩尺比为1∶5的核电站屏蔽厂房双钢板混凝土组合剪力墙试件，研究了竖向荷载、栓钉间距、钢板厚度及加劲肋设置等因素对剪力墙结构的抗侧刚度在低周往复荷载作用下的影响，为以后的研究提供参考资料.

2 试验概况

2.1 试件设计

屏蔽厂房的结构形式为圆筒状，在进行试件设计时在平面上取圆筒的1/360，在高度上取自底部以上10 m范围为研究对象，采用1∶5的缩尺比得出剪力墙墙体的试验设计尺寸为820 mm × 220 mm × 2 000 mm。

试件整体由3部分组成：加载梁、剪力墙墙体、基础梁，具体尺寸分别为1 020 mm × 300 mm × 300 mm，820 mm × 220 mm × 2 000 mm，1 820 mm × 430 mm × 550 mm，9个双钢板混凝土组合剪力墙采用同样的尺寸规格，试件编号分别为SCSW1～SCSW9.9个试件的设计方案如图1所示，试件的具体试验参数如表1所示.试件混凝土强度等级采用C55，钢板采用Q345，钢板和混凝土的材料性能试验参数分别如表2和表3所示.为了研究栓钉间距、钢板厚度、加劲肋的设置以及竖向荷载对剪力墙试件抗侧刚度的影响，本试验设计SCSW1,SCSW2,SCSW3和SCSW7来研究栓钉间距对试件抗侧刚度的影响；设计试件SCSW1,SCSW4和 SCSW6来研究钢板厚度对试件抗侧刚度的影响；设计试件SCSW1,SCSW8 和SCSW9来研究加劲肋的设置对试件抗侧刚度的影响(加劲肋为50 mm × 25 mm × 4 mm的角钢，图2给出了加劲肋的布置图)；设计试件SCSW4和 SCSW5来研究竖向荷载对试件抗侧刚度的影响.

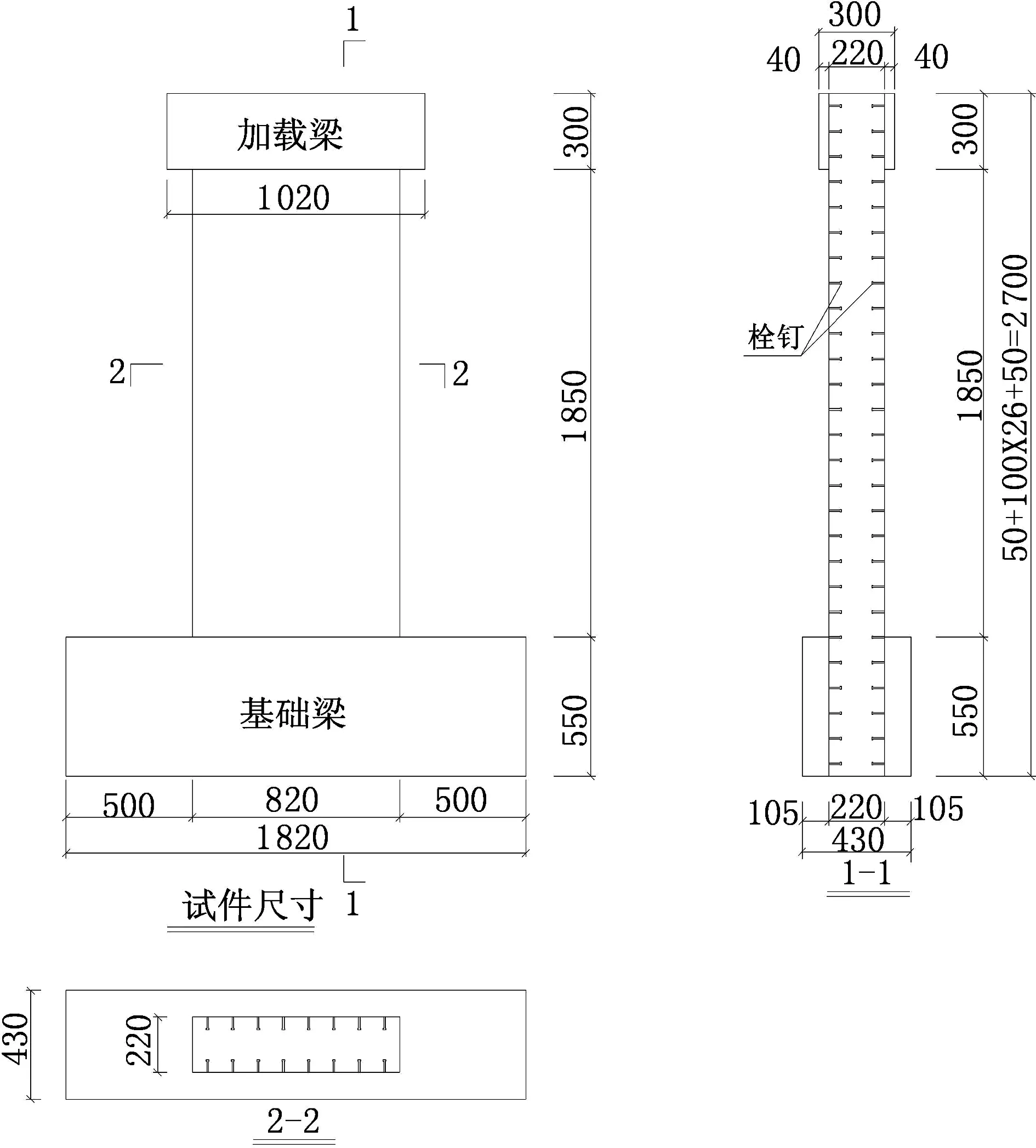
图1 试件设计示意图Fig.1 Design sketch of specimens

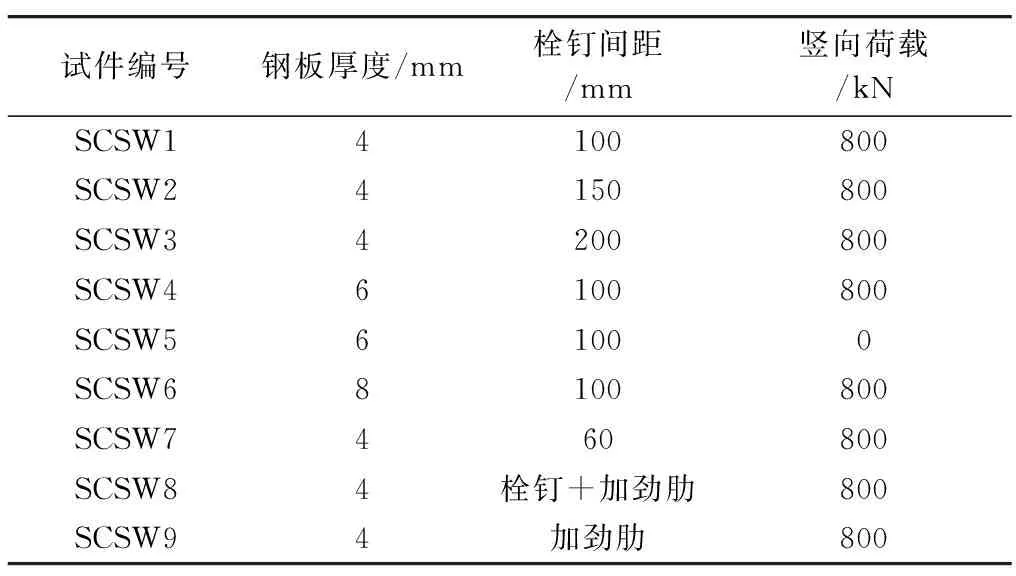
试件编号钢板厚度/mm栓钉间距/mm竖向荷载/kNSCSW14100800SCSW24150800SCSW34200800SCSW46100800SCSW561000SCSW68100800SCSW7460800SCSW84栓钉+加劲肋800SCSW94加劲肋800

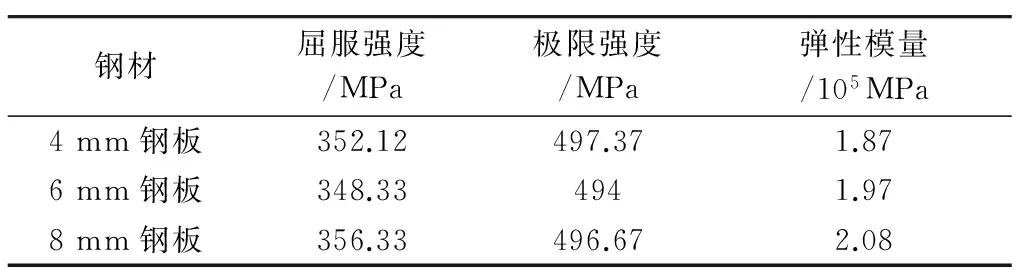
表2 钢板材料性能

表3 混凝土材料性能

图2 加劲肋布置图Fig.2 Layout of stiffeners

总结最新的一些研究成果[12-13]，发现剪力墙试件在低周往复加载过程中很容易从基础梁中拔出甚至基础梁先于剪力墙发生破坏.为了避免这种情况的发生，本试验采取的措施为加强基础梁与剪力墙的锚固.将剪力墙整体贯通基础梁，并且将剪力墙的外钢板与基础梁的底板焊接成整体.

2.2 试验装置和加载制度

拟静力试验是目前研究结构或结构构件抗震性能应用最广泛的试验方法[14].本文采用拟静力试验研究双钢板混凝土组合剪力墙试件的抗震性能.试验于北京工业大学工程抗震与结构诊治北京市重点实验室进行，试验装置主要由两部分组成：竖向加载装置和水平方向加载装置.试验加载设备如图3所示.在实验室现有试验条件的基础上参考JGJ 101-96《建筑抗震试验方法规程》[15]，采用荷载和位移混合加载的控制方法分级加载.初始加载值为50 kN，按照每级50 kN递加并循环一次，直至试件屈服，试件屈服后的位移加载按试件屈服时位移Δy的1/8逐级加载，对于屈服点的确定还没有统一的标准.本试验在对试件的加载过程中，根据数据采集仪器中显示的水平荷载-位移曲线，根据试验数据分析和试件屈服的定义，确定当试件位移增加为前一级位移增加的1.5倍时，试件屈服.当水平荷载从极限荷载下降到峰值荷载的85%时，停止加载，试验结束.

为了研究双钢板混凝土组合剪力墙的抗侧刚度，需要测量出墙顶水平力和位移，另外需测量出基础梁的水平位移以消除试件基础在试验过程中的滑动对墙顶水平位移造成的影响.墙顶和基础梁测点的布置如图4所示.

图3 试验加载装置Fig.3 Load system of tests

图4 荷载和位移测点布置Fig.4 Load and displacement test point arrangement of specimens

2.3 试验现象

试件SCSW1～SCSW9试验过程和试验现象基本相似.试件加载的初级阶段，钢板和混凝土都处于弹性工作状态，两者同步变形.顶点的荷载-位移曲线呈直线变化，无残余变形.随着荷载的增加，钢板和混凝土接触面开始分离，用锤子敲打钢板可以听到“梆梆”的空响声.继续加载，可以发现剪力墙墙体底部钢板出现微小的鼓屈，并且随着荷载的增大，钢板的鼓屈面积和变形逐渐增大；在屈服阶段，墙顶的位移在同样加载幅度的情况下明显增大，试件屈服；在反复加载的作用下，剪力墙墙角底部受压侧钢板焊缝开裂，并且呈对称分布.继续加载裂缝逐渐往上延伸，裂缝部位内部混凝土被压碎；在竖向荷载和水平低周往复荷载作用下，墙体底部混凝土抗压能力迅速下降，墙角钢板裂缝处出现水平裂缝，钢板鼓屈明显增大，混凝土碎块从裂口处流出，试件破坏.在此过程中可以听到“嘣嘣”的声音.试件破坏后，从钢板鼓屈的部位用电焊将鼓屈的钢板切割掉，可以看到钢板鼓屈部位有栓钉从与钢板焊接根部断裂，分析原因应该是栓钉为阻止钢板和混凝土的分离被拉断，如图5所示.

图5 被拉断栓钉Fig.5 The snapped stud

总结双钢板混凝土组合剪力墙试件的破坏过程，可以把整个过程大致划分成5个阶段：弹性阶段、钢板鼓屈阶段、屈服阶段、开裂阶段和破坏阶段.对比9个双钢板混凝土组合剪力墙试件的试验现象，可以发现，试件SCSW1～SCSW7在钢板鼓屈连通后会整体破坏，而试件SCSW8、SCSW9由于配有加劲肋，其延性明显比较好，并且试件底部钢板鼓屈不会连成整体，只会出现局部鼓屈.试件的破坏现象如图6所示.

图6 试件破坏模式Fig.6 Failure modes of specimens

3 抗震性能分析

3.1 水平荷载-位移滞回曲线

分析试验数据时，忽略加载梁在荷载作用下的变形，假定其为刚性.水平荷载V取往复荷载下正反两个方向荷载的平均值.墙顶位移计测出的数据为加载梁的刚体位移，减去试件基础的水平位移得出试件在往复荷载作用下的水平位移δ.

由于篇幅的限制，本文仅给出剪力墙试件SCSW1，SCSW5，SCSW6 和SCSW8在低周往复荷载作用下的水平荷载-位移滞回曲线，如图7所示，其中横坐标为水平荷载对应的水平位移δ，纵坐标为加载梁中心位置的水平荷载V.

(a)SCSW1

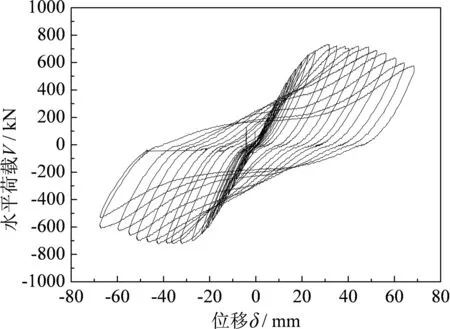
(b)SCSW5

(c)SCSW6

(d)SCSW8图7 试件水平荷载-位移滞回曲线Fig.7 Hysteresis curves of horizontal load-deformation of specimens

由图7可知，在试件的加载初期滞回曲线基本呈直线变化，试件的钢板和混凝土都处于弹性阶段.钢板和混凝土在此阶段由于粘结作用协同工作，受力性能良好.随着荷载的增加，钢板和混凝土出现分离，钢板发生鼓屈现象，但此时钢板和混凝土还有抗剪连接件的连接作用，试件受力性能没有明显变化，抗侧刚度变化不明显.继续加载，混凝土在竖向荷载以及往复荷载作用下逐渐被压碎，钢板鼓屈严重，试件刚度变小，强度增加缓慢，试件开始屈服.滞回环面积逐渐增大，滞回曲线的形状成“S形”.当试件达到极限承载力后，试件刚度和强度开始退化，但退化比较平缓，此时试件还有一定的刚度和强度，滞回曲线没有出现明显的捏缩现象，呈“反S形”发展.

3.2 骨架曲线

为了研究各个参数对剪力墙试件抗震性能的影响，把各级循环加载峰值点依次相连得到了试件在往复荷载作用下的骨架曲线，如图8所示.

图8 试件水平荷载-位移骨架曲线Fig.8 Lateral force-displacement skeleton curves of specimens

从图8中可以看出,试件在屈服前骨架曲线基本上呈直线变化.钢板鼓屈后，曲线斜率开始下降，结构刚度减小，从水平荷载-位移滞回曲线可以看出水平位移在荷载增幅一定的情况下增大较快.试件在达到极限荷载后，荷载下降比较缓慢,下降段比较平缓，说明试件具有良好的变形能力.

比较试件SCSW1，SCSW2，SCSW3和SCSW7的骨架曲线可知，4个试件的骨架曲线差别很小，栓钉间距对试件的抗侧刚度变化基本没有影响.比较试件的极限荷载，随着栓钉间距的减小，极限荷载有所增大，但增加幅度不大；比较试件SCSW1，SCSW8和SCSW9可以看出，加劲肋的设置在很大程度上增大了骨架曲线的斜率，提高了试件的抗侧刚度，而且大幅度提高了试件的极限荷载.SCSW9比SCSW1的极限荷载提高了48.66%；比较SCSW4和SCSW5可以看出，有竖向荷载试件的抗侧刚度比无竖向荷载的试件有所提高，比较试验数据可以发现，极限承载力提高了10.39%；比较SCSW1，SCSW4和SCSW6可知，随着钢板厚度的增加，试件的抗侧刚度和极限承载力都有很大的提高，根据数据显示可知，钢板厚度由4 mm增加到6 mm时，试件的极限承载力提高31.87%；钢板厚度由6 mm增加到8 mm时，试件的极限承载力提高19.14%.

4 双钢板混凝土组合剪力墙初始抗侧刚度的参数分析

4.1 初始抗侧刚度影响因素

为了研究栓钉间距对试件初始抗侧刚度的影响，对比试件SCSW7，SCSW1， SCSW2 和SCSW3的初始抗侧刚度(它们的栓钉间距分别为60 mm，100 mm，150 mm和200 mm).可以发现随着栓钉间距的增加，试件的初始抗侧刚度逐渐减小，但是从数值上看变化并不是很大，如图9所示.因此，可以忽略栓钉间距对双钢板混凝土组合剪力墙试件初始抗侧刚度的影响.

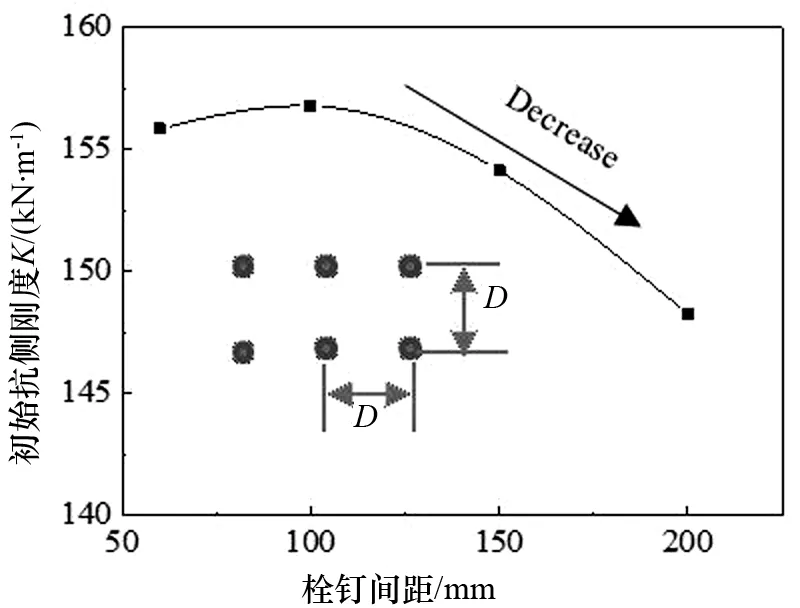
图9 栓钉间距对试件初始抗侧刚度的影响Fig.9 The initial lateral-resisting stiffness of specimens with different stud spacing

为了研究钢板厚度对试件初始抗侧刚度的影响，比较试件SCSW1，SCSW4 和SCSW6的初始抗侧刚度(试件所对应的钢板厚度分别为4 mm，6 mm，8 mm).从图10中可以发现，钢板厚度越厚，试件的初始抗侧刚度越大.钢板厚度从4 mm到6 mm，剪力墙试件的初始抗侧刚度增加7.97%.钢板厚度从6 mm增加到8 mm时，剪力墙试件的初始抗侧刚度提高6.32%.因此，钢板厚度对试件初始抗侧刚度有比较大的影响.

图10 钢板厚度对试件初始抗侧刚度的影响Fig.10 The initial lateral-resisting stiffness of specimens with different plate thickness

图11 加劲肋设置对试件初始抗侧刚度的影响Fig.11 The initial lateral-resisting stiffness of specimens with different stiffening ribs

为了研究加劲肋设置对试件初始抗侧刚度的影响，比较试件SCSW1，SCSW8 和SCSW9的初始抗侧刚度(试件所对应的抗剪连接件结构形式分别为栓钉、栓钉+加劲肋、加劲肋)，从图11中可以看出，加劲肋的设置在很大程度上增大了试件的初始抗侧刚度.比较试件SCSW1和SCSW9可以发现，剪力墙试件的抗剪连接件由栓钉换成加劲肋时，初始抗侧刚度提高了11.7%.因此，加劲肋的设置对试件的初始抗侧刚度影响较大.

为了研究竖向荷载对试件初始抗侧刚度的影响，比较试件SCSW4 (竖向荷载800 kN)，SCSW5(无竖向荷载)的初始抗侧刚度.从表3中的试验数据可以看出，有竖向荷载试件的初始抗侧刚度比无竖向荷载试件的初始抗侧刚度提高了21.97%.因此，竖向荷载在一定程度上提高了试件的初始抗侧刚度.分析其原因：混凝土在竖向荷载作用下，材料之间的相互作用更加紧密，使试件刚度增大.但从理论上分析，如果竖向荷载增大到一定程度会对混凝土造成破坏，从而减小试件的抗侧刚度.本文由于试验试件参数变化数量的限制，不能得出更精确的结论，需要进一步研究竖向荷载的增加对剪力墙试件抗侧刚度的影响.

4.2 分析模型基本假定

核岛结构中屏蔽厂房的剪力墙结构形状为圆筒状，墙体下部固定在刚度较大的基础上，上部没有约束条件.为了能够从理论上研究双钢板混凝土组合剪力墙试验试件的初始抗侧刚度，对剪力墙试件进行了简化模型处理，假定：1)忽略试验过程中竖向荷载对试件上端水平位移的影响，试件上端采用滑动约束；忽略试验过程中试件下端支座可能的滑移，试件下端采用固定约束；2)不考虑混凝土和钢板的损伤对抗侧刚度的影响，视钢板和混凝土都处于弹性状态.剪力墙试件的简单化模型如图12所示.实际的剪力墙试件有竖向荷载和水平低周往复荷载作用,将其简化为悬臂梁并按照单位荷载的方法计算墙顶的水平位移：

(1)

根据JGJ 138-2001《型钢混凝土组合结构技术规程》[16]，型钢混凝土构件截面的抗弯刚度和抗剪刚度可以按照下列公式计算：

EI=EsIs+EcIc

(2)

GA=GsAs+GcAc

(3)

图12 剪力墙试件的简化模型Fig.12 Simplified model of specimen

式中：E，Es和Ec分别为剪力墙试件的弹性模量、钢板的弹性模量和混凝土的弹性模量；I，Is和Ic分别为剪力墙试件的截面惯性矩、钢板的截面惯性矩和混凝土的截面惯性矩；G，Gs和Gc分别为剪力墙试件的剪切模量、钢板的剪切模量和混凝土的剪切模量；A，As和Ac分别为剪力墙试件的截面面积、钢板的截面面积和混凝土的截面面积；k为剪应力系数，当剪力墙截面为矩形时[12]取值1.2.

(4)

根据设计的剪力墙试件的结构形式得出钢板和混凝土截面惯性矩分别为：

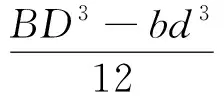
(5)

式中：B和D分别为剪力墙试件矩形截面的宽度和长度；b和d分别为剪力墙试件内部混凝土截面的宽度和长度；Is1和Is2分别为设计试件和实际试件中钢板所对应的截面惯性矩；As1和As2分别为设计试件和实际试件中钢板的截面面积.

图13 试件截面形式转换Fig.13 Section changing of specimen

根据设计剪力墙试件的截面形式和实际墙体截面形式的关系，取α=1.63，β=1.2.并将α，β以及式(5)代人式(4)得：

(6)

其中t为单层钢板的厚度.

可以得到双钢板混凝土组合剪力墙的初始抗侧刚度公式为：

(7)

4.3 初始抗侧刚度计算分析

为了验证推导出的拟合公式的准确性，基于试验试件的相关参数，利用本文得到的公式计算相应的初始抗侧刚度值，并与试验值进行比较，结果如表4所示.

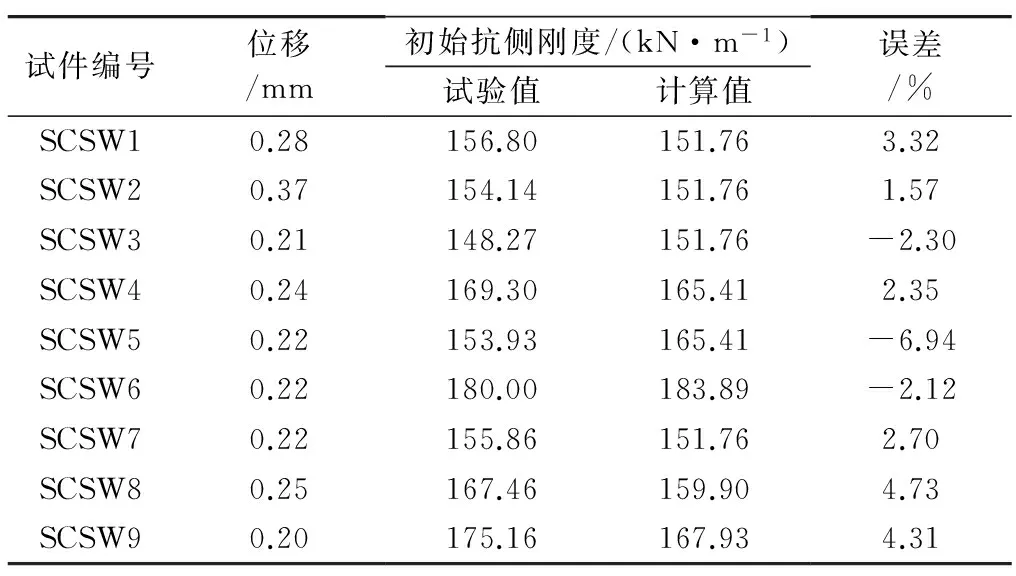
表4 试验值和计算值比较

从表4中可以看出，试验值和计算值的误差在10%以内，说明公式(7)能够很好地拟合双钢板混凝土组合剪力墙的初始抗侧刚度.从表4中分析发现，双钢板混凝土组合剪力墙试件初始抗侧刚度所对应的位移大概都在0.25 mm附近，因此可以得出双钢板混凝土组合剪力墙的初始抗侧刚度可以取位移角为1/8 000时所对应的抗侧刚度.

5 双钢板混凝土组合剪力墙有限元分析

5.1 有限元模型建立

本文采用ABAQUS有限元软件对核岛结构双钢板混凝土剪力墙试件进行了数值模拟.混凝土、钢板、栓钉都采用C3D8单元.建立模型时忽略加载梁和基础梁的变形，以及实际加载过程中基础梁的滑动位移.直接将加载点和剪力墙墙体顶面中心点进行耦合，用来施加竖向荷载和水平荷载.基础梁底面的约束采用完全固定的方式.试件的边界条件和加载形式如图14所示.

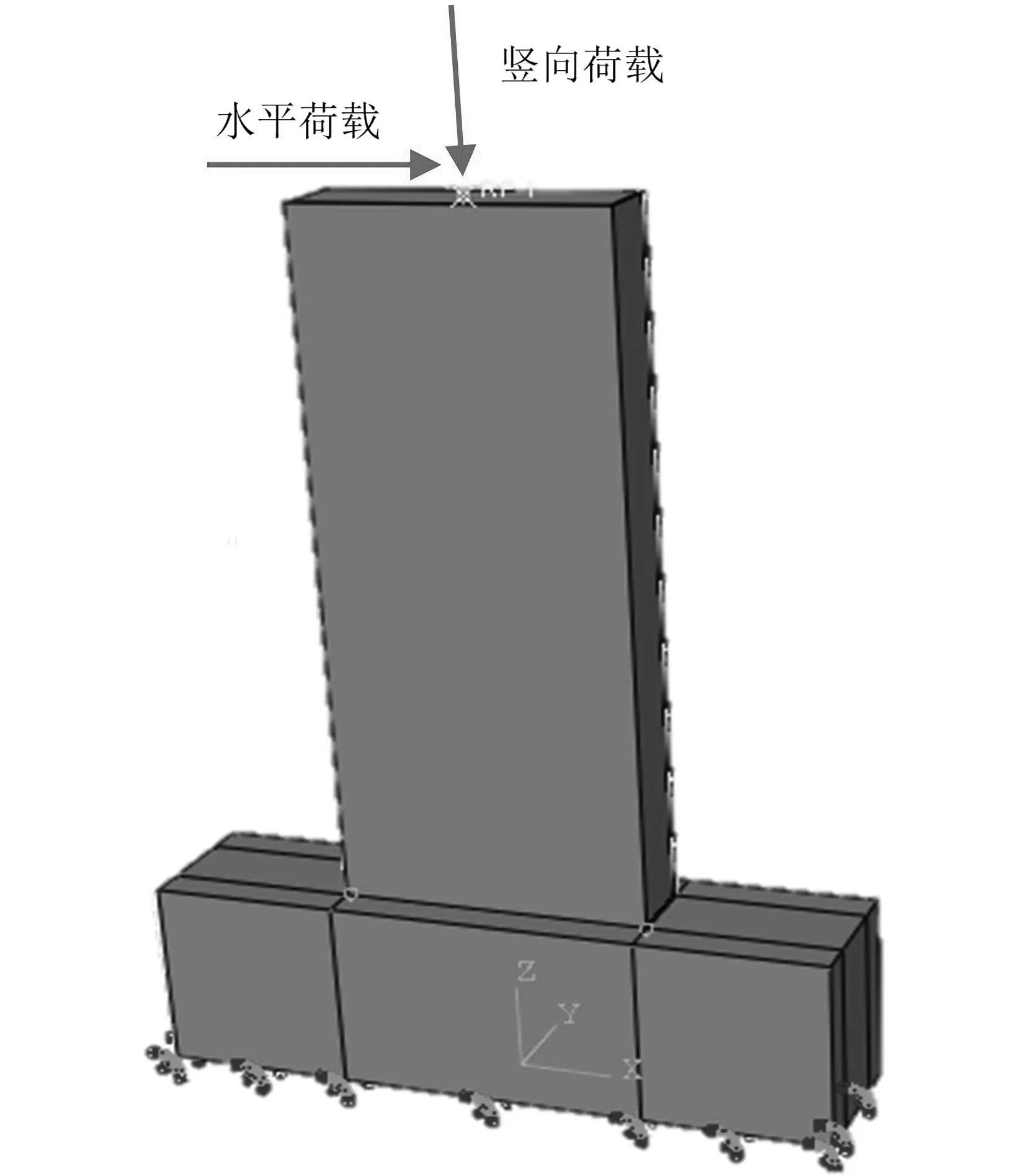
图14 边界条件和加载方式Fig.14 Boundary conditions and loading form

混凝土本构采用塑性损伤模型，本构关系曲线参考GB 50010-2010《混凝土结构设计规范》的相关规定，其中的特征参数采用试验数据.混凝土的弹性模量取3.25×104MPa，泊松比取0.2；钢材的弹性模量取1.87×105MPa，泊松比取0.3.钢板和混凝土之间的接触关系在法向方向采用硬接触来模拟，切线方向采用摩擦模型，接触面摩擦因数采用0.6.

5.2 结果分析

从双钢板混凝土组合剪力墙试件的有限元模型的应力云图可以看出，剪力墙在墙体根部应力最大，和试验结果比较吻合.试件SCSW1破坏时的应力图如图15所示.

图15 试件SCSW1破坏时应力图Fig.15 The failure stress of SCSW1

(a)SCSW1

(b)SCSW4

(c)SCSW6

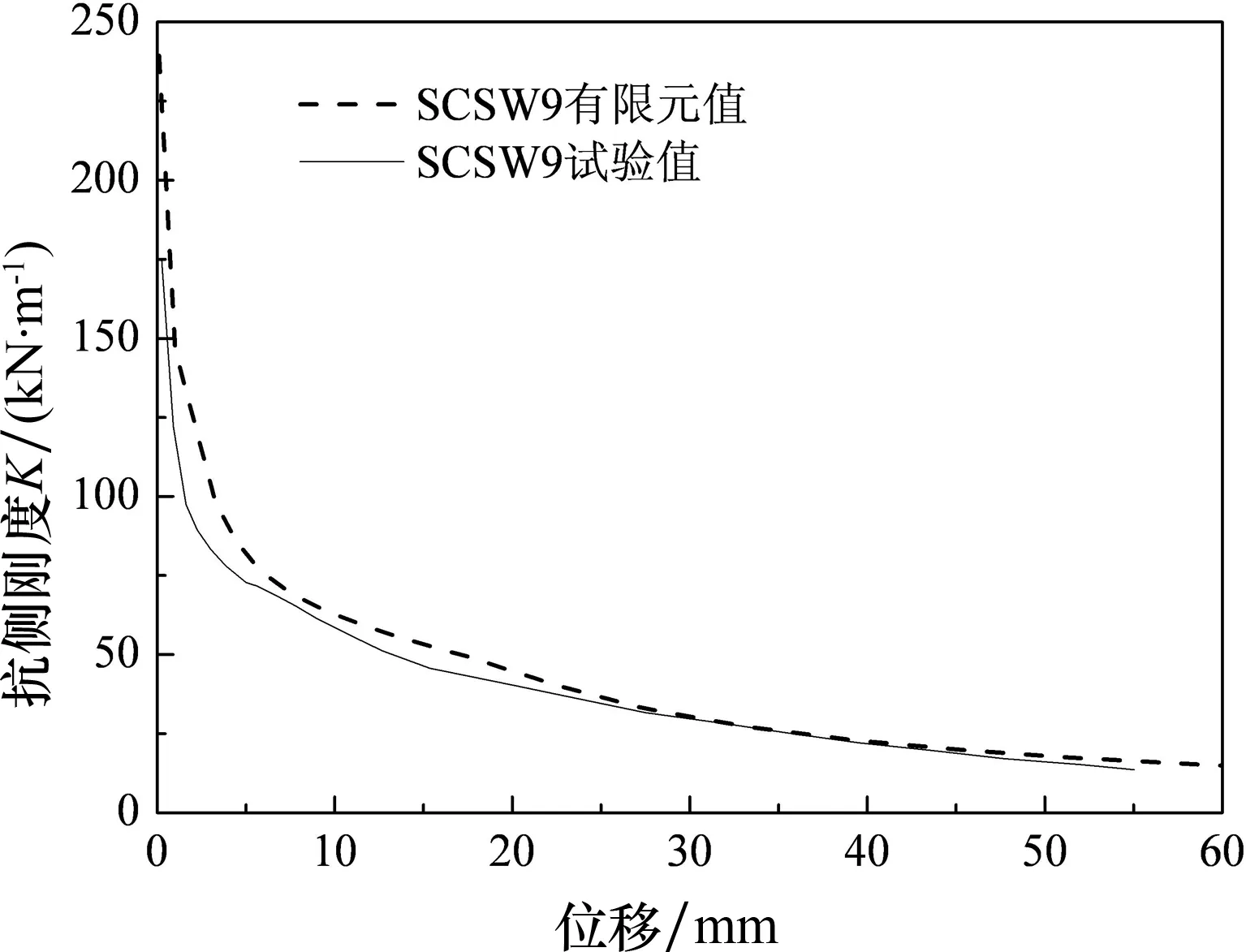
(d)SCSW9图16 各试件抗侧刚度有限元值和试验值Fig.16 Finite element results and test results of the lateral stiffness of specimens

图16给出了试件SCSW1,SCSW4 ,SCSW6和SCSW9抗侧刚度的有限元模拟和试验结果的比较.通过比较可以发现，有限元模拟的初始抗侧刚度大于试验结果，统计所有的试件结果表明，有限元模拟的初始抗侧刚度大概是试验结果的1.0～1.4倍，平均1.2倍，如表5所示.这是由于在对试件进行有限元模拟时忽略了材料的初始缺陷.有限元模拟的抗侧刚度在缓慢下降阶段更加平缓，这是由于在实际试验中，试件内部混凝土被压碎，试件的抗侧刚度急剧下降.说明有限元模拟中采用的混凝土损伤模型和实际试验中混凝土的损伤还有一定的差别.从整体来看，有限元模拟和试验结果的曲线比较接近，因此在试验条件不允许的情况下有限元模拟可以作为参考，但是更精确的有限元模拟需要更加接近真实材料的本构关系.

表5 试件初始抗侧刚度的试验值和有限元值

6 双钢板混凝土组合剪力墙抗侧刚度分析

本文采用割线刚度的方法[17]计算双钢板混凝土组合剪力墙试件的抗侧刚度.根据JGJ 101-1996 《建筑抗震试验方法规程》的规定，取循环加载中的各单周两个方向的荷载绝对值之和与位移绝对值之和的比值作为试件单周加载的割线刚度，用Ki表示，其计算公式如下：

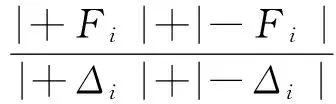
式中：+Fi和-Fi分别为第i级循环推和拉方向的峰值荷载；+Δi和-Δi分别为+Fi和-Fi所对应的位移.

选用割线刚度和试件顶部的水平位移(推拉两个方向位移绝对值的平均值)之间的关系来研究试件在往复荷载作用下的抗侧刚度变化情况，如图17所示.

图17 各试件抗侧刚度退化曲线图Fig.17 The lateral stiffness degradation of specimens

从图17可以看出，各剪力墙试件在往复荷载的加载过程中抗侧刚度的变化趋势基本一致，随着位移的增加剪力墙试件的抗侧刚度有退化的现象.根据图17中趋势线的形状可以将各个试件在加载过程中的退化过程大致分为3个阶段：1)急速下降阶段.开始加载，钢板和混凝土由于粘结作用共同工作，此时试件的抗侧刚度最大.此阶段试件位移变化较小，但抗侧刚度变化幅度大，为抗侧刚度变化曲线的直线段.2)缓速下降阶段.此阶段钢板和混凝土在往复荷载作用下发生分离，混凝土只是开裂但尚未破坏，钢板也没有发生屈服现象，混凝土和钢板还能够较好地发挥其相应的力学性能，试件抗侧刚度下降比较缓和.此阶段从试件开始屈服直到试件达到极限荷载.3)平缓下降阶段.此阶段混凝土在反复加载下破坏，并且钢板发生鼓屈并屈服，试件的抗侧刚度在此阶段逐渐变小，但变化不大，直至试件完全破坏.此阶段从试件达到极限荷载直到试件完全破坏.

比较本试验和核电工程双钢板混凝土组合剪力墙最新研究成果可以发现[12]，剪力墙抗侧刚度的整体变化趋势大致都可以分为3个阶段，但各个阶段抗侧刚度的变化幅度有所不同，本文抗侧刚度的缓速下降阶段并不是特别明显，试件延性没有文献[12]的试件延性好.另外，本文试件初始抗侧刚度的取值要大于文献[12]初始抗侧刚度的取值.这方面的差别主要在于双钢板混凝土组合剪力墙试件的结构，本试验考虑了两侧以外的剪力墙对剪力墙试件的约束影响，但对于此约束的精确取值和准确的试验设计还有待深入研究.

7 结 论

通过对9个双钢板混凝土组合剪力墙试件低周往复荷载的试验，研究和分析了剪力墙试件在荷载作用下抗侧刚度的变化过程，得出如下结论：

1)从试件的试验结果可以发现，试验结束后，剪力墙基础基本没有损伤.由此可以看出，对基础外包钢板的设计，完全满足了剪力墙在低周往复荷载作用下对锚固条件的要求.

2)各因素对双钢板混凝土组合剪力墙试件初始抗侧刚度的影响：栓钉间距对初始抗侧刚度的影响不是很明显，但钢板厚度和加劲肋的设置对初始抗侧刚度有较大影响，竖向荷载对初始抗侧刚度也有一定的影响，但具体影响需要深入研究.

3)在试验设计的基础上，对试件进行简化假设，从理论上推出了剪力墙试件初始抗侧刚度的计算公式，经试验结果比较发现，本文所给出的公式计算结果和试验结果吻合较好.

4)对试件进行了有限元数值分析，通过比较试件抗侧刚度的有限元值和试验结果发现，有限元模拟的初始抗侧刚度大于试验结果.有限元模拟的抗侧刚度退化比试验结果更加平缓.

5)分析试件在往复荷载作用下的抗侧刚度变化过程，将其划分成3个阶段：急速下降阶段、缓速下降阶段和平缓下降阶段.比较双钢板混凝土组合剪力墙的最新研究成果并分析其差别，需要对两侧剪力墙对剪力墙试件的约束作用进行深入研究.

[1] 高宁.钢板混凝土结构在AP1000核电站中的应用[C]//2010年核电站新技术交流研讨会.深圳:山东核电有限公司,2010:430-439.

GAO Ning.The application of steel reinforced concrete structure in AP1000 nuclear power station[C]//2010 Conference on New Technology of Nuclear Power Plant.Shenzhen:Shandong Nuclear Power Company LTD,2010:430-439. (In Chinese)

[2] 聂建国,陶慕轩,樊健生,等.双钢板-混凝土组合剪力墙研究新进展[J].建筑结构,2011,41(12): 52-60.

NIE Jianguo,TAO Muxuan,FAN Jiansheng,etal. Research advances of composite shear walls with double steel plates and filled concrete[J]. Building Structure,2011,41(12):52-60. (In Chinese)

[3] 丁朝辉,江欢成,曾菁,等.双钢板-混凝土组合墙的大胆尝试-盐城电视塔结构设计[J].建筑结构,2011,41(12):87-91.

DING Chaohui,JIANG Huancheng,ZENG Jing,etal. An innovative application of SCS composite wall: Structural design of Yancheng TV Tower[J]. Building Structure,2011,41(12):87-91. (In Chinese)

[4] 曹德金,席永慧.组合剪力墙的抗震研究简述[J].山西建筑,2012,38(24):45-48.

CAO Dejin,XI Yonghui. Outline on the seismic research of composite shearing wall[J].Shanxi Architecture,2012,38(24):45-48. (In Chinese)

[5] DANAY A. Response of steel-concrete composite panels to in-plane loading[J]. Nuclear Engineering and Design,2012，242:52-62.

[6] 刘圆圆,张春明,李君利,等.CAP1400核电厂辐射防护审评关键技术及软件系统研发初探[J]. 核电子学与探测技术,2014,34(2): 138-142.

LIU Yuanyuan,ZHANG Chunming,LI Junli,etal. Primary study on key points and software system development of radiation protection review for CAP1400 NPP [J]. Nuclear Electronics & Detection Technology,2014,34(2):138-142.(In Chinese)

[7] HOSSAIN K M A,WRIGHT H D.Experimental and theoret-ical behavior of composite walling under in-plane shear[J].Journal of Constructional Steel Research,2004,60:59-83.

[8] OZAKI M,AKITA S,OSUGAH,etal.Study on steel plate reinforced concrete panels subjected to cyclic in-plane shear[J].Nuclear Engineering and Design,2004,228(1):225-244.

[9] 司波,白正仙.双层钢板剪力墙的初始抗侧刚度分析[J].长春工程学院学报:自然科学版,2006,7(1):8-11.

SI Bo,BAI Zhengxian.Analysis of initial stiffness against lateral displacement of double steel plate shear wall[J].Changchun Institute of Technology:Natural Science Edition,2006,7(1):8-11.(In Chinese)

[10] 罗永峰,李健,郭小农.双层钢板-内填混凝土组合剪力墙滞回性能数值分析[J].湖南大学学报:自然科学版,2014，41(6):57-62.

LUO Yongfeng,LI Jian,GUO Xiaonong.Numerical analysis of hysteretic performance of double-steel-layer-concrete compo-site shear wall[J].Journal of Hunan University:Natural Sciences,2014,41(6):57-62.(In Chinese)

[11] 程春兰,周德源,朱立猛.带约束拉杆双钢板混凝土组合剪力墙抗震性能数值模拟及参数分析[J].湖南大学学报:自然科学版,2016,43(9):10-17.

CHENG Chunlan,ZHOU Deyuan,ZHU Limeng.Numerical simulation and parameter analysis on seismic behavior of composite concrete and double steel plates shear walls with binding bars [J]. Journal of Hunan University:Natural Sciences,2016,43(9):10-17.(In Chinese)

[12] 张有佳,李小军.双钢板混凝土墙体构件抗震性能试验研究[J].武汉大学学报:工学版,2015,48(5):658-665.

ZHANG Youjia,LI Xiaojun.Experimental research on seismic behavior of wall component with double steel plate and infill concrete [J].Engineering Journal of Wuhan University,2015,48(5):658-665.(In Chinese)

[13] 熊峰,何涛,周宁.核电站双钢板混凝土剪力墙抗剪强度研究[J].湖南大学学报:自然科学版,2015,42(9):33-41.

XIONG Feng,HE Tao,ZHOU Ning. Study on the shear strength of double steel plate composite shear wall in nuclear plant [J]. Journal of Hunan University:Natural Sciences,2015,42(9):33-41.(In Chinese)

[14] 赵刚,潘鹏,聂建国,等.基于力和位移混合控制的多自由度结构拟静力试验方法研究[J].土木工程学报,2012,45(12):54-62.

ZHAO Gang,PAN Peng,NIE Jianguo,etal. Force-displacement mixed control method for quasi-static tests of structures with multiple degrees of freedom[J].China Civil Engineering Journal,2012,45(12):54-62.(In Chinese)

[15] JGJ 101-1996 建筑抗震试验方法规程[S].北京：中国建筑工业出版社,1997:9-13.

JGJ 101-1996 Specification of testing methods for earthqu-ake resistant building[S].Beijing:China Architecture & Building Press,1997:9-13.(In Chinese)

[16] JGJ 138-2001 型钢混凝土组合结构技术规程[S].北京：中国建筑工业出版社,2001:40-44.

JGJ 138-2001 Technical specification for steel reinforced concrete composite structures[S].Beijing: China Architecture & Building Press,2001:40-44. (In Chinese)

[17] 龙驭球,包世华.结构力学(上册)[M].北京：高等教育出版社,2006:57-97.

LONG Yuqiu,BAO Shihua.Structural mechanics (I) [M]. Beijing: Higher Education Press,2006:57-97.(In Chinese)

Lateral Stiffness of Composite Shear Walls with DoubleSteel Plates and Filled Concrete for a Nuclear Island Structure

LI Xiaojun1,2,LI Xiaohu1†,ZHANG Huiying1

(1. College of Architecture and Civil Engineering,Beijing University of Technology,Beijing 100124,China;2. Institute of Geophysics,China Earthquake Administration,Beijing 100081,China)

In order to study the ability to resist lateral force of nuclear shielding workshop under earthquake action，the low-cyclic loading tests of nine 1/5 scaled composite shear walls with double steel plates and filled concrete were carried out. This paper studied the influence of several parameters such as stud space，thickness of the palate and stiffener on initial lateral stiffness of specimens. The results showed that the initial stiffness of composite shear walls increased with the thickness of steel plates and stiffening rib setting，but the factor of stud space had no obvious effect on it. The calculation formula of initial stiffness of composite shear walls with double steel plates and filled concrete was derived by using unit load method，theoretical hypothesis and simplified precondition. The calculation value was consistent with the experimental value. Moreover，the change process of lateral stiffness of shear wall specimens under cyclic loading was studied and it was found that the changing degree of the stiffness was different in the different stages of the change process of lateral stiffness.

composite shear walls with double steel plates and filled concrete; low-cyclic loading test ;initial lateral stiffness; lateral stiffness

TU398

A

1674-2974(2017)11-0055-11

10.16339/j.cnki.hdxbzkb.2017.11.007

2016-09-05

国家自然科学基金资助项目(51738001,51421005)， National Natural Science Foundation of China (51738001,51421005)；国家科技重大专项(2013ZX06002001)，National Science and Technology Major Project of China (2013ZX06002001)

李小军(1965—)，男，湖南临湘人，中国地震局地球物理研究所研究员，博士生导师

†通讯联系人， E-mail: xiaohu12066@126.com