SCARA并联机构拓扑分析与其低耦合度机型设计

李 菊 曾氢菲 沈惠平 杨廷力

(常州大学现代机构学研究中心， 常州 213016)

SCARA并联机构拓扑分析与其低耦合度机型设计

李 菊 曾氢菲 沈惠平 杨廷力

(常州大学现代机构学研究中心， 常州 213016)

根据基于方位特征(Position and orientation characteristics，POC)的并联机构拓扑结构设计理论与方法，首先，对已提出的一类7个具有较好实用价值的SCARA并联机构，进行了拓扑结构分析，揭示了其POC集、自由度(含驱动副选取)、过约束数、耦合度以及输入-输出运动解耦性等5个最主要的拓扑特征，且发现这些机构的耦合度均较大，为2，表明其运动学正解和动力学求解十分复杂；继而基于机构拓扑结构降耦原理，又对κ=2的这7个机构进行了拓扑结构降耦优化，得到了低耦合度(κ=1)，而机构POC、自由度(Degree of freedom，DOF)等保持不变的实现SCARA运动的14个新机型，不仅丰富了实现SCARA运动的4-DOF三平移一转动机型库，而且降低了这些机构的运动学和动力学代数求解难度，而其数值解可用一维搜索法方便求得，从而为这一类SCARA并联机构的运动学和动力学分析、设计及应用提供了理论基础。

并联机构； POC方法； 拓扑结构分析； 耦合度； 拓扑特征； 机构综合

引言

以方位特征集(POC集)为数学工具、以有序单开链(Single open chain, SOC)为机构组成单元的并联机构(Parallel kinematic machine, PKM)拓扑结构设计理论与方法，由杨廷力等[1-2]提出并建立，该方法不同于基于螺旋理论的方法[3-5]、基于位移子群的方法[6]、基于线性变换和进化算法的方法[7]，它描述的运动都是相对于动平台运动副轴线的，与定坐标系以及机构的运动位置无关，因而是一种几何方法；该方法以简单的POC集的“并”与“交”符号类线性运算，得到非瞬时的无过约束机构和一般过约束机构，物理意义明确，易于理解和应用，为并联机构的设计与分析提供了一种有效而系统的理论与方法。

一方面，纯三平移、纯三转动及SCARA运动(三平移一转动，转动轴线为动平台的法线)为3种典型的输出运动，在工业生产线上具有极广的应用前景。对于实现前两者运动的三自由度并联机器人，已有较多的研究和应用，而对于实现SCARA型输出运动的四自由度并联机器人，其机型的研究和应用开发相对较少。

1999年，ABB 公司开发了称为FlexPicker的SCARA并联机器人[8]，它是在三平移Delta[9]并操作手的基础上，通过动平台与静平台之间再串联一条R-U-P-U-R支链，构成了一个具有三平移一转动功能的混联操作手，实际上，这种混联操作手可视为具有2个动平台(即Delta机构的三平移子平台和转动输出的抓取操作器平台)，这种机型已广泛应用。为克服这种操作手中间支链易磨损、只能适用于较小工作空间的缺点，文献[10-12]设计了H4、I4、Par4等系列的四自由度SCARA型(即三平移一转动)操作手，它们在结构上保留了三平移Delta机构所含的平行四边形结构R∥-(4S)-∥R或R∥R-(4R)-∥R(S为球副，R为转动副)复杂支链，因而在性能上继承了Delta机构高速、动态性能好等优点，也因此被称为Delta族机器人。

2000年，赵铁石等[13]提出了4-URU型三平移一转动并联机器人；2001年金琼等[14]基于方位特征输出矩阵(后称为POC集)和单开链理论，提出了一类三平移一转动并联机器人，并于2003年申请了一组5个具有单动平台的三平移一转动并联机构[15]专利，但未研制样机；黄田等[16]在H4、I4、Par4等结构的基础上，于2010年设计了四自由度三平移一转动的Cross-IV型高速搬运机器人并实现了产业化；刘辛军等[17]于2012年在国内首次研制出具有一个动平台且实现三平移一转动的X4型并联机构样机，并通过尺寸性能优化，实现了较大角度的输出转动[18]。

笔者团队根据基于方位特征(POC)的并联机构拓扑结构设计理论与方法，提出了一类具有较好应用前景的13个四自由度SCARA型(三平移一转动)并联机构，其中7种新机构已申请中国发明专利[19-25]。

文献[26]已对商业化著名并联机构，例：Delta、Diamond、Tricept、TriVariant、Exechon、Z3、H4、Steward等，以及其他具有潜在应用价值的并联机构，进行了详细的拓扑结构分析，得到了一些有价值的结论、规律或启示。

同时，文献[27-28]在研究如何降低机构拓扑结构复杂性的基础上，提出了将机构的结构降耦和机构的运动解耦，作为并联机构拓扑结构优化的两个重要内容，研究表明：①机构的耦合度越大，其运动学正解和动力学求解越复杂，降低机构的结构耦合度可直接降低机构运动学、动力学求解的难度。②耦合度κ恰为机构冗余回路的虚拟变量数或约束回路的运动相容方程数，对于κ=1的机构，可一维搜索法较易求得其位置正解或动力学正、逆解的数值解。③对于κ≥2的任意机构，可将其降为κ=1且保持自由度和运动输出不变，同时，提出了降低机构耦合度κ的3种方法[29]。

本文首先对提出的7个具有较好实用价值的三平移一转动并联机构进行拓扑结构分析，揭示出其POC集、自由度、耦合度等最主要的拓扑结构特征；为进一步简化这些机构的运动学正解和动力学求解，对其进行结构降耦优化，得到POC、DOF不变，但耦合度降至κ=1的低耦合度机型，以期为这些机型的性能评价和优选、运动学与动力学的方便求解，及其设计和应用提供理论基础。

1 并联机构的拓扑特征

本文所述的并联机构拓扑结构特性分析，即为分析并揭示并联机构的12个基本拓扑结构特征[2]，它包括：方位特征集(POC集)及其维数、独立回路数v、独立位移方程数ξL1、过约束数Nov.、自由度(DOF)类型和数目F、基本运动链(Basic kinematic chain, BKC)类型及其数目、BKC耦合度κ、输入-输出运动解耦性(I-O解耦性)、消极运动副、驱动副选择、冗余度等指标，其中[26]：

(1)POC集及其维数，反映了机构的基本功能。

(2)独立位移方程数、冗余度、BKC耦合度、I-O解耦性、驱动副选择，反映了机构运动学与动力学性能。

(3)DOF类型及数目、BKC耦合度、冗余度、POC集维数、I-O解耦性，反映了机构的控制性能。

(4)过约束数Nov.，反映了机构的刚度，以及制造误差对精度的敏感度：Nov.越大，刚度越大，但对制造误差的敏感度越高。

限于篇幅，仅介绍重要的POC集、DOF数、过约束数Nov.、耦合度κ、I-O解耦性这5个指标，其相应的计算公式[1-2]如表1所示。

表1 机构的拓扑结构特征指标Tab.1 Indexes of topological structure characteristicsof mechanisms

2 SCARA并联机构的拓扑分析

笔者团队最近综合得到了10个新机构[19-25]，以下仅对7个具有较好使用价值的Ⅰ～Ⅶ型单动平台SCARA型并联机构进行拓扑结构分析，且按机构组成描述、POC集、DOF数、过约束数Nov.、耦合度κ、I-O解耦性分析等方面来阐述。

2.1 Ⅰ型3T1R机构

2.1.1I型3T1R机构的组成描述

I型3T1R机构如图1所示[19]，它由静平台0、动平台1以及4条结构相同的支链组成；从静平台0到动平台1，前3个转动副相互平行，后2个转动副相互平行，但第3、4个转动副轴线垂直；4条支链的一端通过转动副R15、R25、R35、R45与动平台1连接，这4个转动副的轴线须平行于动平台1平面的法线；4条支链的另一端通过驱动副R11、R21、R31、R41与静平台0连接，其中，R11⊥R21，R31⊥R41。

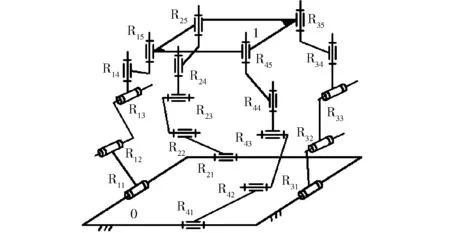
图1 I型3T1R并联机构Fig.1 Type Ⅰ 3T1R parallel mechanism

2.1.2I型3T1R机构的DOF、Nov.、POC计算

(1)机构的拓扑结构

SOC{-Ri1‖Ri2‖Ri3⊥Ri4‖Ri5-}
(i=1, 2, 3, 4)

(2)确定支链末端构件的POC集

约定：动平台1上任意一点O′为基点，下同。

(3)确定第1回路的独立位移方程数ξL1

①由第1、2支链构成第1回路

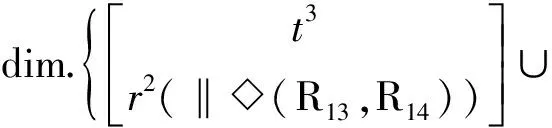
②第1、2支链构成的子PKM的DOF和POC

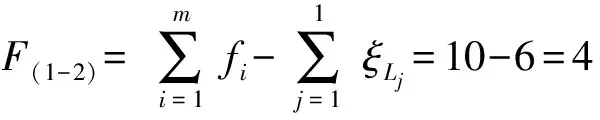
(4)确定第2回路的独立位移方程数ξL2

①由第3支链再构成第2回路

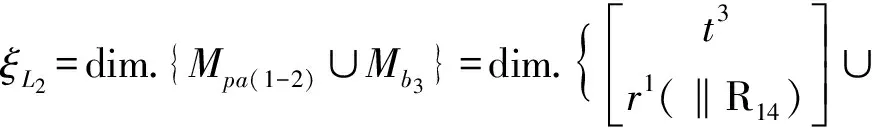
②第1、2、3支链构成的子PKM的DOF和POC

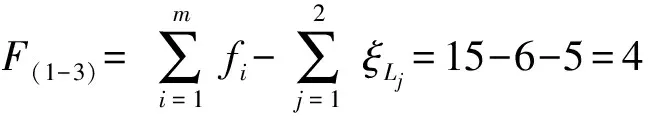
(5)确定第3个回路的独立位移方程数ξL3

由第4支链再构成第3回路

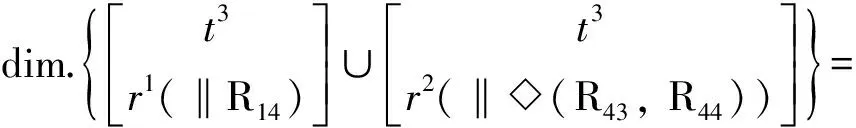
(6)确定机构的自由度

(7)确定机构过约束数Nov.

(8)确定该机构动平台的POC集

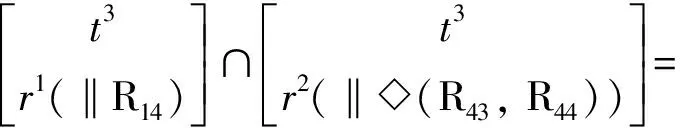
因此，根据驱动副的选择准则[1-2]，当静平台0上的转动副R11、R21、R31、R41为驱动时，该机构动平台1产生3个平移和1个绕动平台1法线的转动。

2.1.3Ⅰ型3T1R机构的κ计算、I-O解耦性分析

(1)确定第1回路及其约束度Δ1

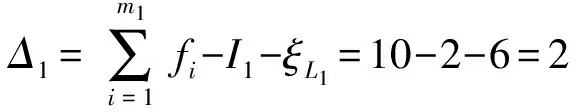
(2)确定第2回路及其约束度Δ2

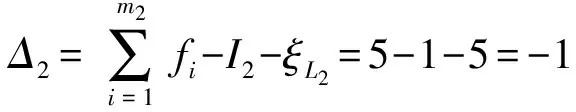
(3)确定第3回路及其约束度Δ3

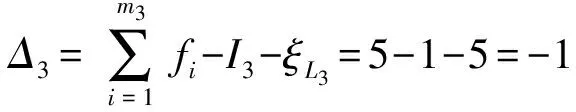
(4)确定机构包含的BKC及其耦合度κ

这样，该机构只包含一个BKC；由于4个驱动副均在一个BKC内，因此，无I-O解耦性。

该机构的拓扑结构特性如表2所示。

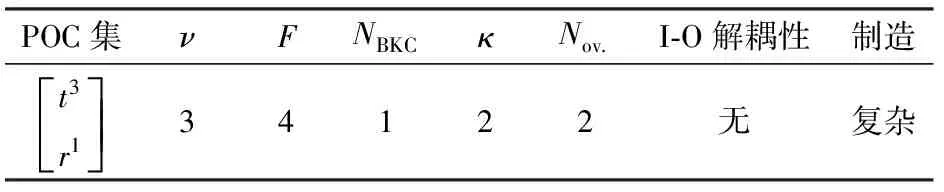
表2 I型3T1R机构的拓扑结构特征Tab.2 Topological structure characteristics oftype Ⅰ 3T1R mechanism

2.2 Ⅱ型3T1R机构

2.2.1Ⅱ型3T1R机构的组成描述

Ⅱ型3T1R机构如图2所示[19]，它可视为用2条RSS无约束支链，替代图1机构中的2条约束支链而得。动平台1上的转动副R15、R35的轴线，须平行于动平台1平面的法线；静平台0上的转动副R11⊥R31，但R21、R41可任意布置。

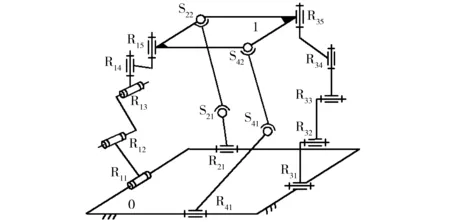
图2 Ⅱ型3T1R机构Fig.2 Type Ⅱ 3T1R parallel mechanism

2.2.2Ⅱ型3T1R机构的DOF、Nov.、POC计算

(1)机构的拓扑结构

1、3支链同为SOC{-Ri1‖Ri2‖Ri3⊥Ri4‖Ri5-}(i=1,3)；其余2条无约束支链为SOC{-S-S-R-}。

(2)确定支链末端构件的POC集

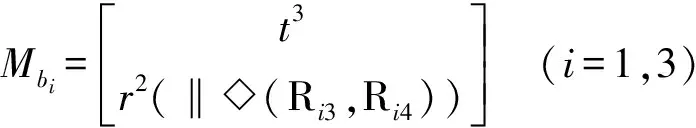
(3)确定第1个回路的独立位移方程数ξL1

①由第1、3支链构成第1回路

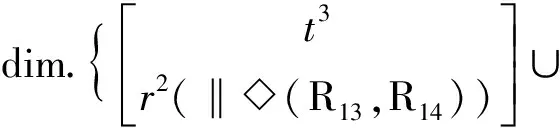
②第1、3支链构成的子PKM的DOF和POC

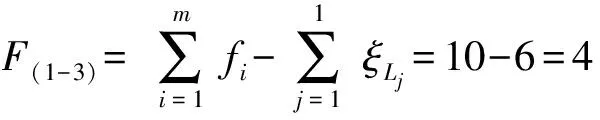
(4)确定第2个回路的独立位移方程数ξL2

①由第2支链再构成第2回路

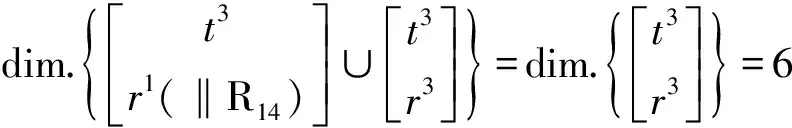
②第1、3、2支链构成的子PKM的DOF和POC

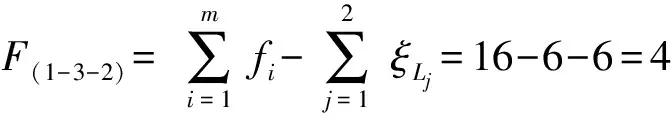
(5)确定第3个回路的独立位移方程数ξL3

由第4支链再构成第3回路

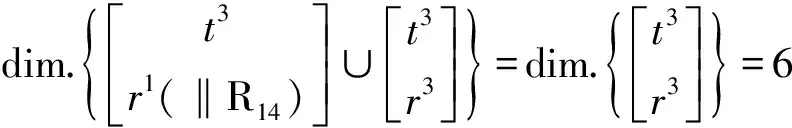
(6)确定机构的自由度

(7)确定机构过约束数Nov.

(8)确定并联机构动平台的POC集

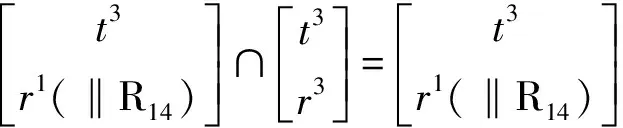
因此，当取静平台0上的R11、R21、R31、R41为驱动副时，该机构作三平移一转动的运动。

2.2.3Ⅱ型3T1R机构的κ计算、I-O解耦性分析

(1)确定loop1及其约束度Δ1

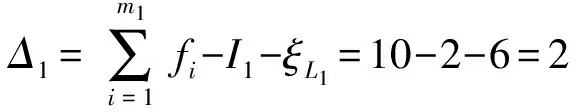
(2)确定loop2及其约束度Δ2

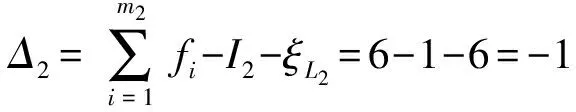
(3)确定loop3及其约束度Δ3

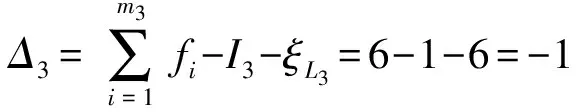
(4)确定机构包含的BKC及其耦合度κ

因该机构只包含一个BKC，同样无I-O解耦性。

该机构的拓扑结构特性如表3所示。

表3 Ⅱ型3T1R机构的拓扑结构特性Tab.3 Topological structure characteristics of type Ⅱ 3T1R mechanism

2.3 Ⅲ、IV型3T1R机构

2.3.1Ⅲ型3T1R机构的组成描述

Ⅲ型3T1R机构如图3所示[20]，它由动平台1、静平台0、4条结构相同且包含由4个转动副组成的平行四边形的复杂支链组成；动平台1上的4个转动副R13、R23、R43、R33的轴线须平行于动平台1平面的法线；静平台0上的4个转动副R11、R21、R41、R31平行于动平台1上4个转动副的轴线。

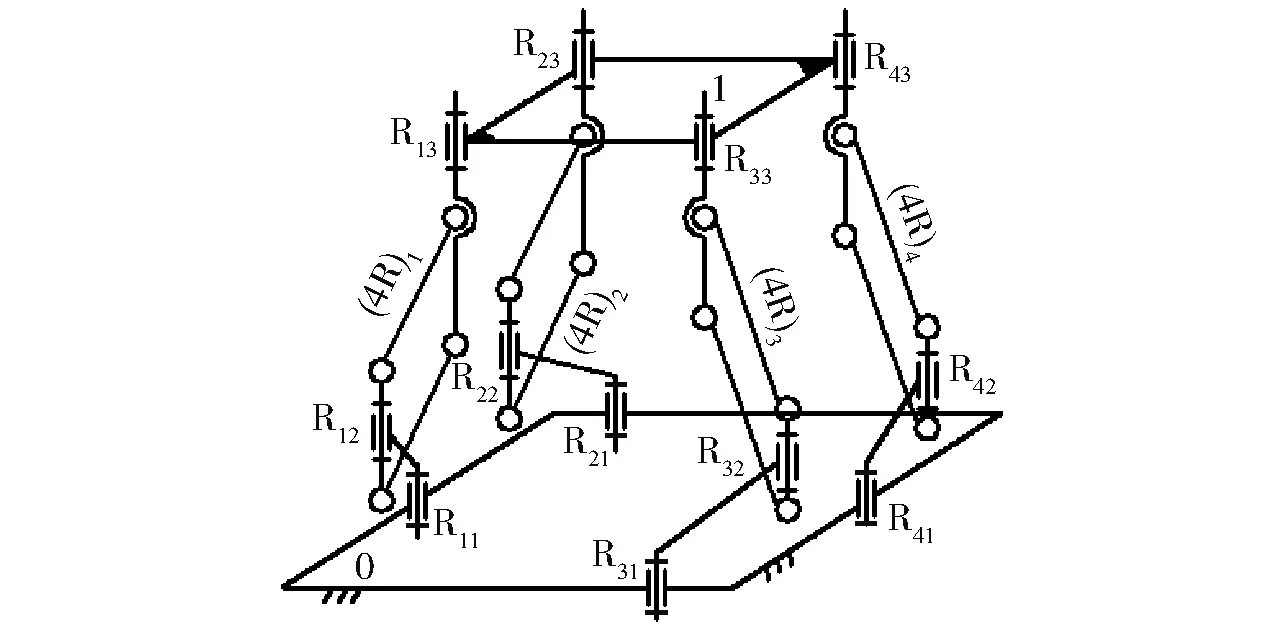
图3 Ⅲ型3T1R机构Fig.3 Type Ⅲ 3T1R parallel mechanism

2.3.2Ⅲ型3T1R机构的DOF、Nov.、POC计算

(1)机构的拓扑结构

4条支链同为：SOC{-Ri1‖Ri2(-◇(4R)i)-‖Ri3}(i=1,2,3,4)。

(2)确定支链末端构件的POC集

(3)确定第1个回路的独立位移方程数ξL1

①第1、2支链构成第1回路

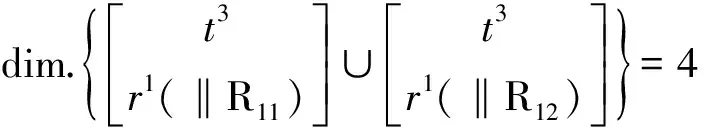
②第1、2支链构成的子PKM的DOF和POC

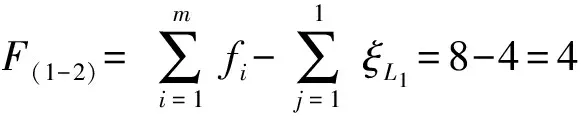
(4)确定第2个回路的独立位移方程数ξL2

①由第3支链构成第2回路

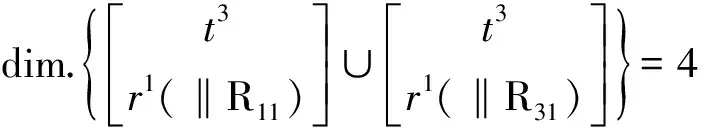
②第1、2、3支链构成的子PKM的DOF和POC

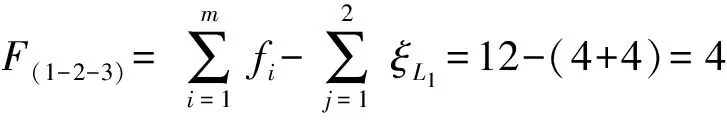
(5)确定第3个回路的独立位移方程数ξL3

由第4支链构成第3回路

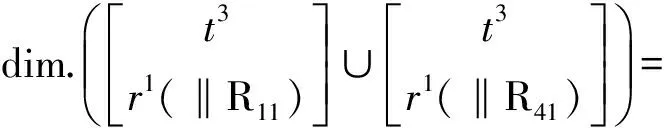
(6)确定机构自由度F

(7)确定机构的过约束数Nov.

(8)确定动平台POC集

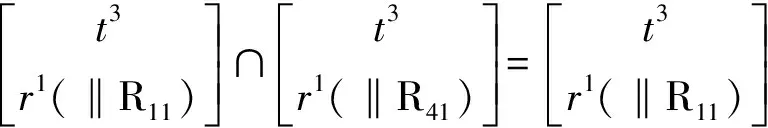
因此，当选取静平台0上的4个转动副R11、R21、R31、R41为驱动副时，该机构作三平移一转动的运动。

2.3.3Ⅲ 型3T1R机构κ计算、I-O解耦性分析

(1)确定loop1及其约束度Δ1

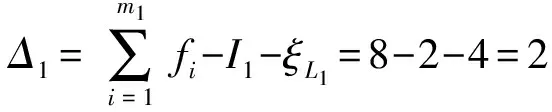
(2)确定loop2及其约束度Δ2

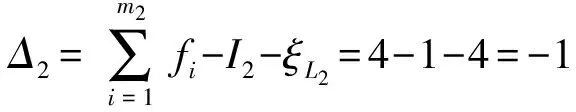
(3)确定loop3及其约束度Δ3

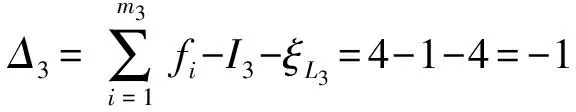
(4)确定所含BKC及其耦合度κ

该机构含有一个BKC，同样，无I-O解耦性。

该机构的拓扑结构特性如表4所示。

同样，用2条RSS无约束支链，替代图3所示机构中的2条约束支链，即得到如图4所示的Ⅳ型3T1R机构[20]，显然，该机构的拓扑结构特性同Ⅲ 型3T1R机构一样，如表4所示。

表4 Ⅲ型3T1R机构的拓扑结构特征Tab.4 Topological structure characteristics oftype Ⅲ 3T1R mechanism

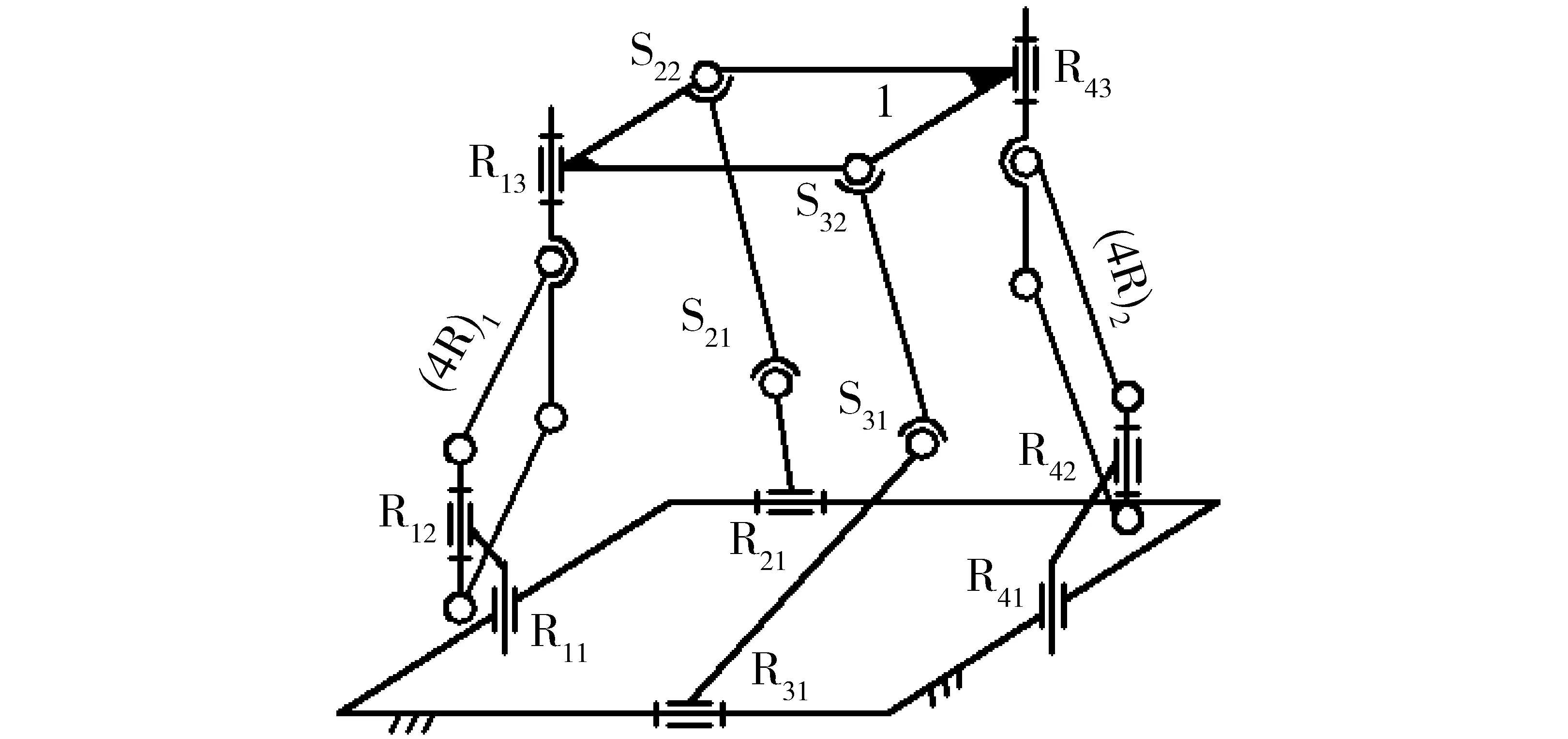
图4 Ⅳ型3T1R机构Fig.4 Type Ⅳ 3T1R parallel mechanism

2.4 Ⅴ型、Ⅵ型3T1R机构

2.4.1V型3T1R机构的组成描述

V型3T1R机构如图5所示[21]，它由动平台1、静平台0、4条结构相同且包含由4个转动副组成的平行四边形的复杂支链组成；动平台1上的4个转动副R14、R24、R34、R44的轴线须平行于动平台1平面的法线；静平台0上的转动副配置为R11⊥R31、R21⊥R41。

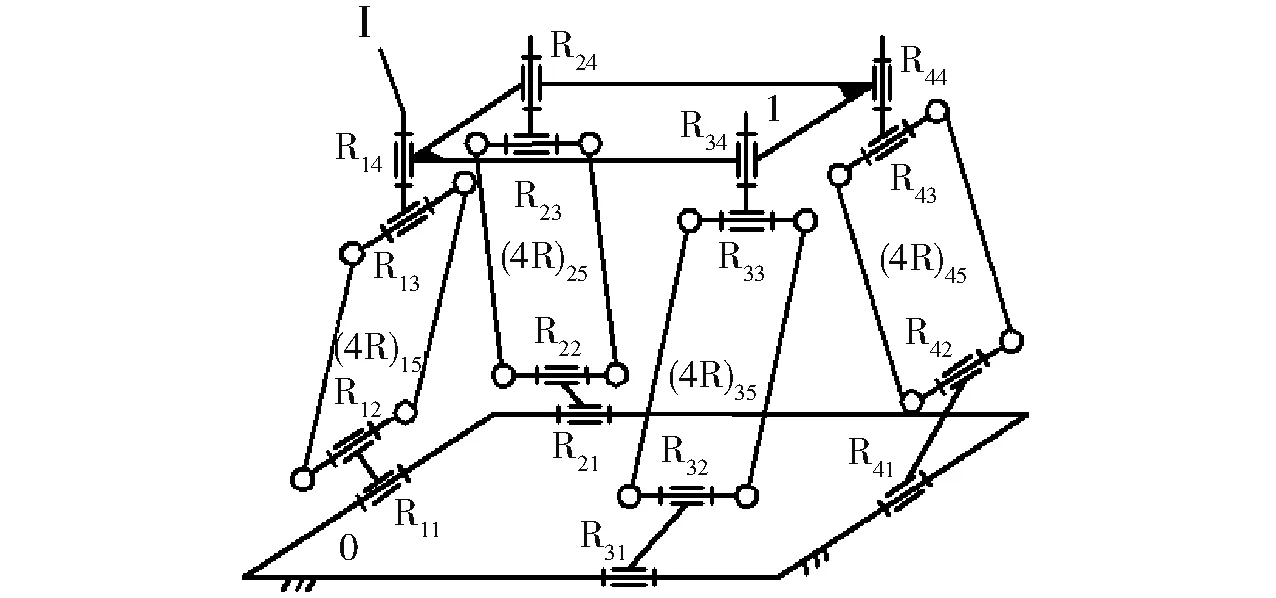
图5 V型3T1R机构Fig.5 Type Ⅴ 3T1R parallel mechanism

2.4.2V型3T1R机构的DOF、Nov.、POC计算

(1)机构拓扑结构

4条支链相同，为：SOC{-Ri1-Ri2(-◇(4R)i5-) ‖Ri3⊥Ri4-}(i=1,2,3,4)。

(2)确定支链末端构件的POC集

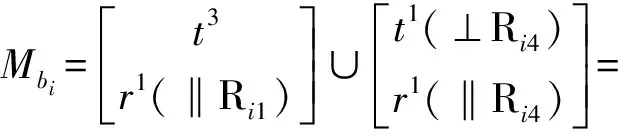
(3)确定第1个回路的独立位移方程数ξL1

①由第1、2支链构成第1回路

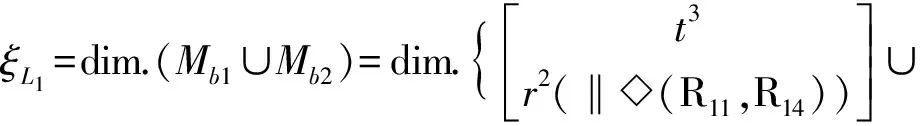
②第1、2支链构成的子PKM的DOF和POC

Mpa(1-2)=

(4)确定第2个回路的独立位移方程数ξL2

①由第3支链构成第2回路

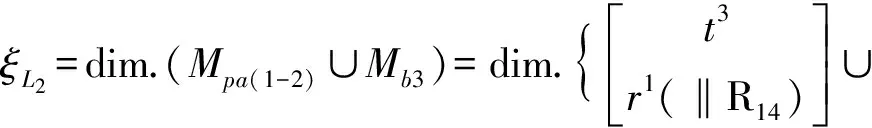
②第1、2、3支链构成的子PKM的DOF和POC

(5)确定第3个回路的独立位移方程数ξL3

由第4支链构成第3回路

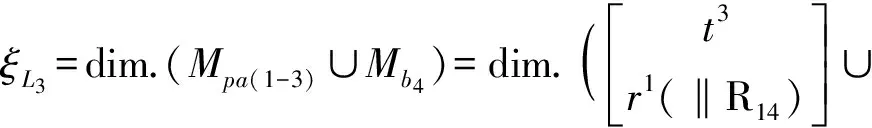
(6)确定机构自由度F

(7)确定机构的过约束数Nov.

(8)确定动平台POC集

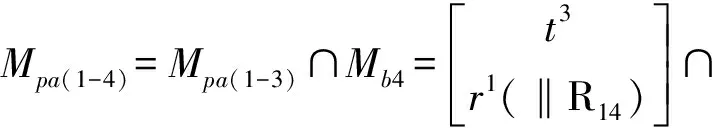
因此，取静平台0上的4个转动副R11、R21、R41、R31为驱动副时，该机构作三平移一转动运动。

2.4.3V型3T1R机构的κ计算、I-O解耦性分析

(1)确定loop1及其约束度Δ1

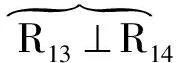
(2)确定loop2及其约束度Δ2

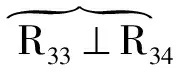
(3)确定loop3及其约束度Δ3

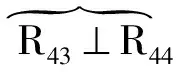
(4)确定机构BKC及其耦合度κ

因该机构只包含一个BKC，也无I-O解耦性。

该机构的拓扑结构特性如表5所示。

表5 V型3T1R机构的拓扑结构特性Tab.5 Topological structure characteristics oftype Ⅴ 3T1R mechanism

需要说明的3种情况是：

(1)同样，用2条RSS无约束支链，替代图5所示机构中的2条约束支链，即得到如图6所示的Ⅵ-1型3T1R机构[21]，显然，该机构具有与V型3T1R机构一样的拓扑结构特性，如表5所示。

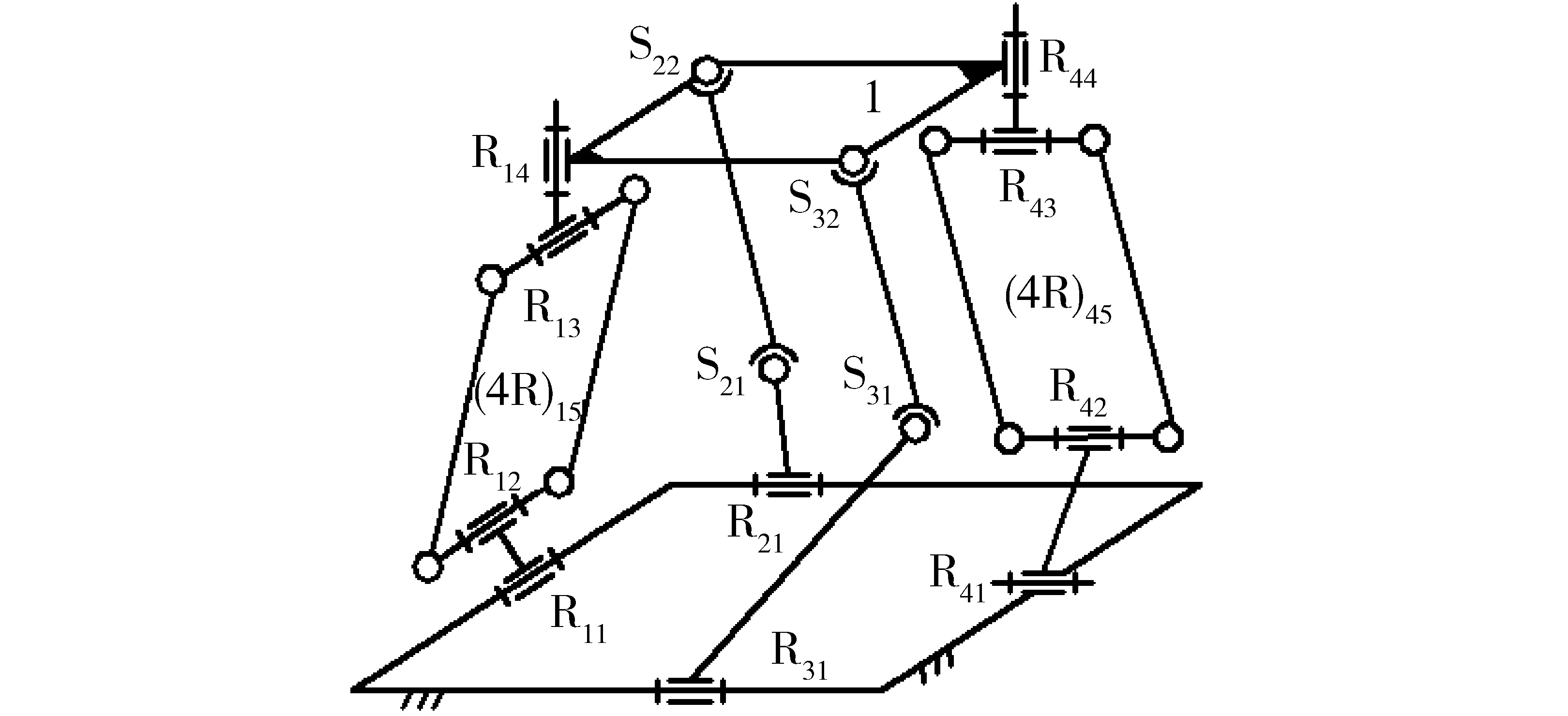
图6 Ⅵ-1型3T1R机构Fig.6 Type Ⅵ-1 3T1R parallel mechanism

(2)将图5所示机构中的平行四边形复杂支链短边上的转动副，例：支链I上的转动副R13及其两端的转动副，等效为2个球副，如图7中的Sa、Sb，即成为图7所示的Ⅵ-2型3T1R机构[22]，显然，它们具有与V型3T1R机构相同的DOF、POC、κ、Nov.及I-O解耦性。

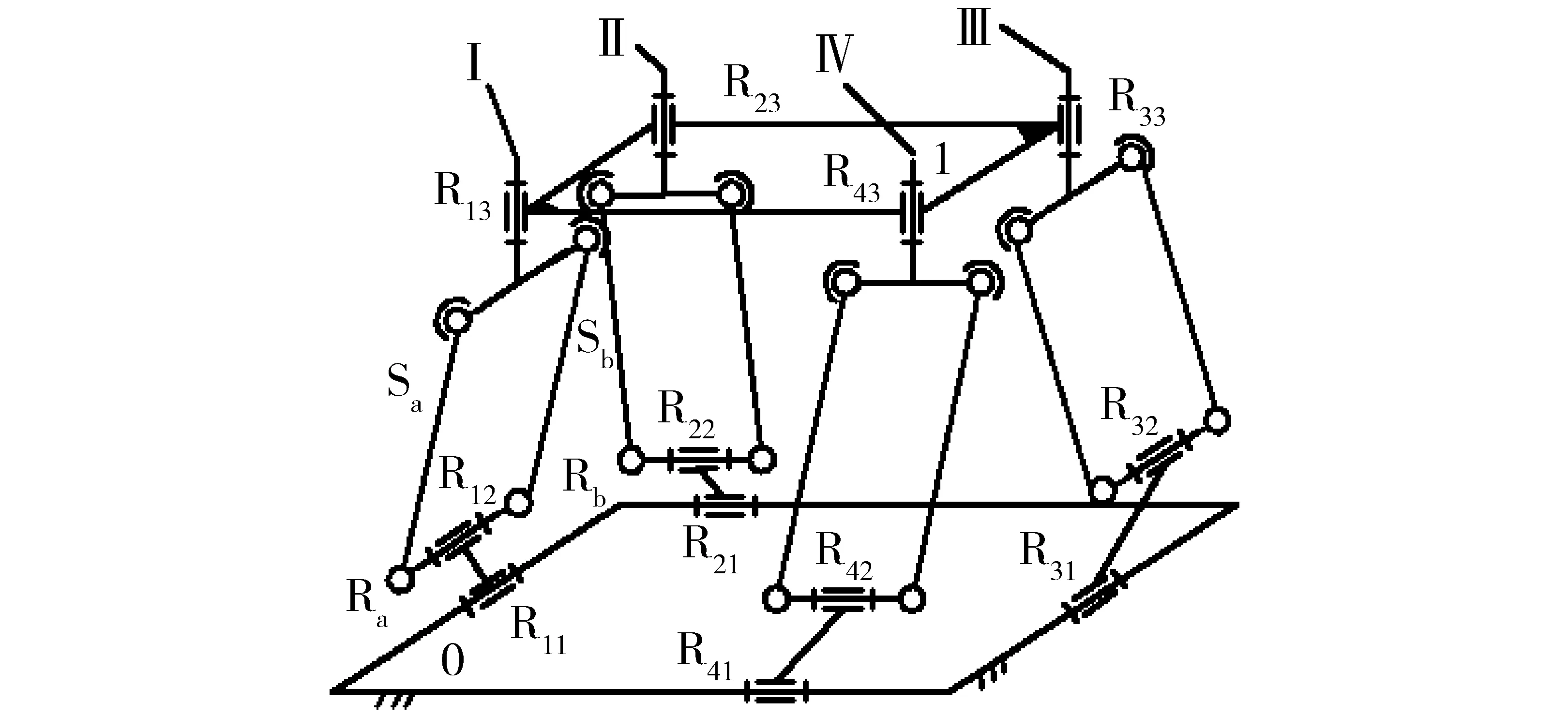
图7 Ⅵ-2型3T1R机构Fig.7 Type Ⅵ-2 3T1R parallel mechanism

(3)将图7所示机构中的2条垂直配置的复杂支链，例：Ⅱ、Ⅲ支链，用R-S-S无约束支链代替(例，图8中的R21-S22-S23，R41-S42-S43)，即成为图8所示的Ⅵ-3型3R1T机构[23]，同样，其DOF、POC、Nov.、κ、BKC、I-O解耦性，与图5～7所示机构相同，其计算从略。

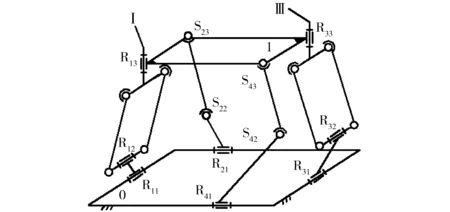
图8 Ⅵ-3型3T1R机构Fig.8 Type Ⅵ-3 3T1R parallel mechanism

2.5 Ⅶ型3T1R机构

2.5.1Ⅶ型3T1R机构的组成描述

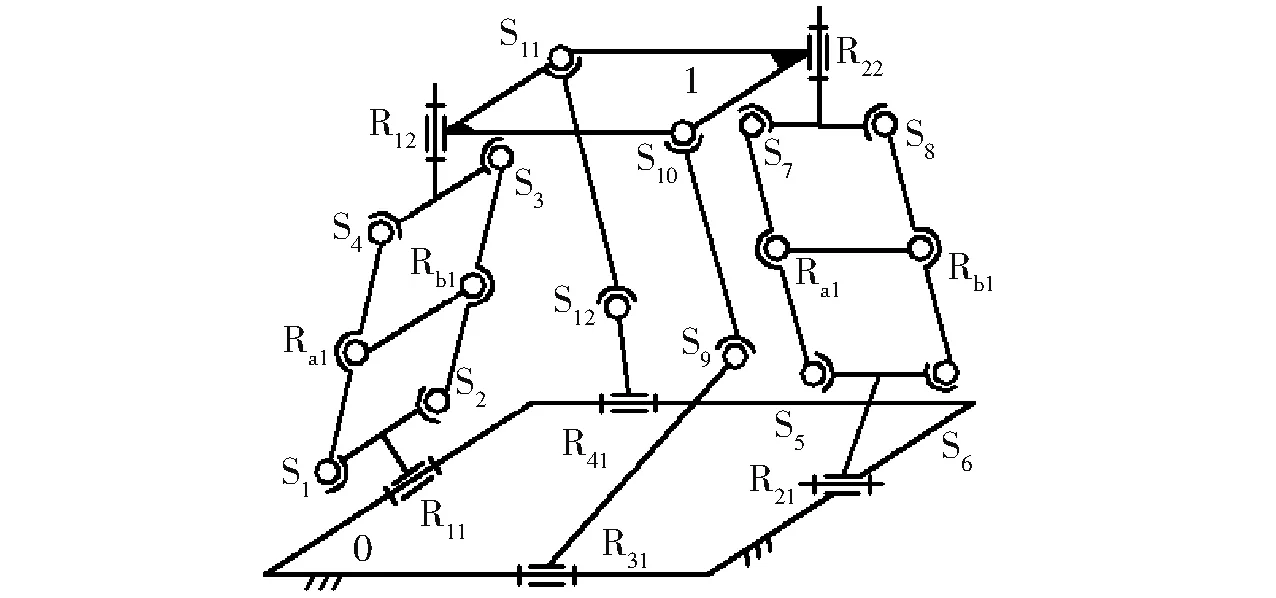
图9 VII型3T1R机构Fig.9 Type Ⅶ 3T1R parallel mechanism

Ⅶ型3T1R机构如图9所示[24]，它由动平台1、静平台0、2条RSS型无约束支链，以及2条包含由4个球副组成的平行四边形的复杂支链组成；装配时，为使4个球副S的球心构成平行四边形，必须在平行四边形中配置一杆带两转动副(Ra、Rb)的结构(其长度等于其一边长度即可)；动平台1上的转动R12、R22的轴线须平行于动平台1平面的法线；静平台0上的转动副R11⊥R21，但R31、R41可任意布置。

2.5.2Ⅶ型3T1R机构的DOF、Nov.、POC计算

(1)机构的拓扑结构

2条复杂支链为HSOC1{-R11‖◇(-S1,S2,S3,S4)-R12}、HSOC2{-R21‖◇(-S5,S6,S7,S8)-R22}；其余2条为无约束支链SOC{-R31-S9-S10-}、SOC{-R41-S12-S11-}。

(2)确定支链末端构件的POC集、HSOC1、HSOC2末端构件的POC集为

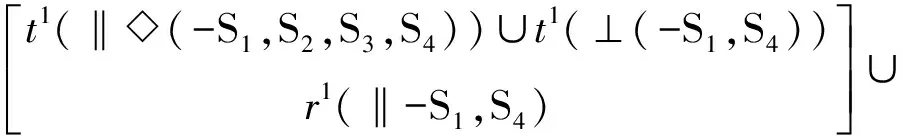
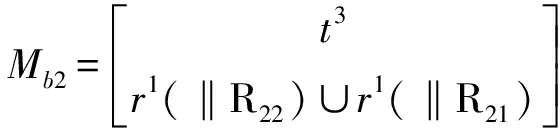
2条无约束支链末端构件的POC集为

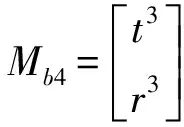
(3)确定第1个回路的独立位移方程数ξL1

①由第1、2支链构成第1回路

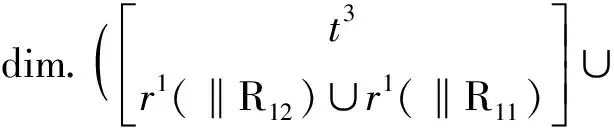
②第1、2支链构成的子PKM的DOF和POC为

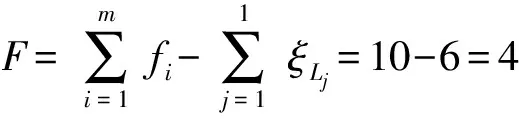
(4)确定第2个回路的独立位移方程数ξL2

①由第3支链构成第2回路

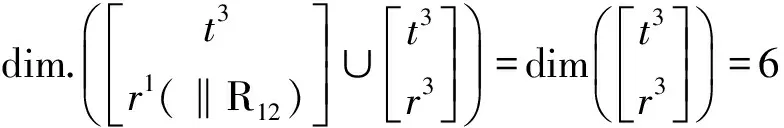
②第1、2、3支链构成的子PKM的DOF和POC

Mpa(1-3)=Mpa(1-2)∩Mb3=

(5)确定第3个独立回路的独立位移方程数ξL3

由第4支链构成第3回路

ξL3=dim.(Mpa(1-3)∪Mb4)=

(6)确定机构自由度F

(7) 确定机构的过约束数Nov.

(8)确定动平台POC集

Mpa=Mpa(1-3)∩Mb4=

因此，当取R11、R21、R31、R41为驱动副时，该机构作三平移一转动的运动。

2.5.3Ⅶ型3T1R机构κ计算、I-O解耦性分析

(1)确定第1回路及其约束度Δ1

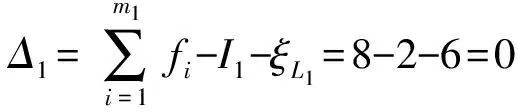
(2)确定第2回路及其约束度Δ2

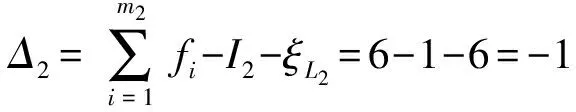
(3)确定第3回路及其约束度Δ3

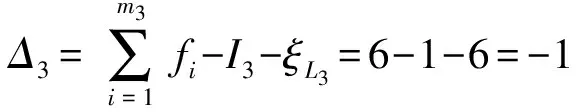
(4)确定所含基本运动链(BKC)及耦合度κ

该机构仅含有一个BKC，也无I-O解耦性。该机构的拓扑结构特性如表6所示。

实现SCARA运动的X4机构[17]，具有4条完全相同的上述复杂支链；而该机构仅具有2条复杂支链，因此，该机构可看作是X4并联机构的改进与优化，其构造简单，制造维修更为容易。

表6 Ⅶ型3T1R并联机构的拓扑结构特性Tab.6 Topological structure characteristics of type Ⅶ 3T1R mechanism

至此，已完成7个(Ⅰ～Ⅶ)具有较好实用价值的4-DOF三平移一转动并联机构的拓扑结构特性分析，为寻求其低耦合度的新机型设计与优化奠定了基础。

3 基于结构降耦的拓扑优化

由第2小节分析可知，这7个单动平台的3T1R机构，其耦合度均较高，为κ=2，这意味着这些机构运动学正解或动力学正、逆解，其代数求解困难，数值求解也需要用二维搜索法才能求解，计算过程不易收敛并占时较多[2, 26]。

为此，本文运用结构降耦方法之一——机构运动副复合法[27-28, 30]，对这7种3T1R机构进行拓扑结构降耦，得到了14个结构更简单、耦合度低(κ=1)、运动学或动力学求解不复杂、但DOF和POC均不变的新机构。限于篇幅，现仅举以下2例说明。

3.1 I型3T1R并联机构的降耦设计

将图1所示的I型3T1R并联机构中，垂直配置的2条支链在动平台1上的转动副R15和R25重合(称为：一次降耦)，形成一条含空间回路的复杂支链，得到的机构如图10所示[31]，显然，机构的DOF、POC、Nov.等均不变，但耦合度发生了变化，现计算如下：

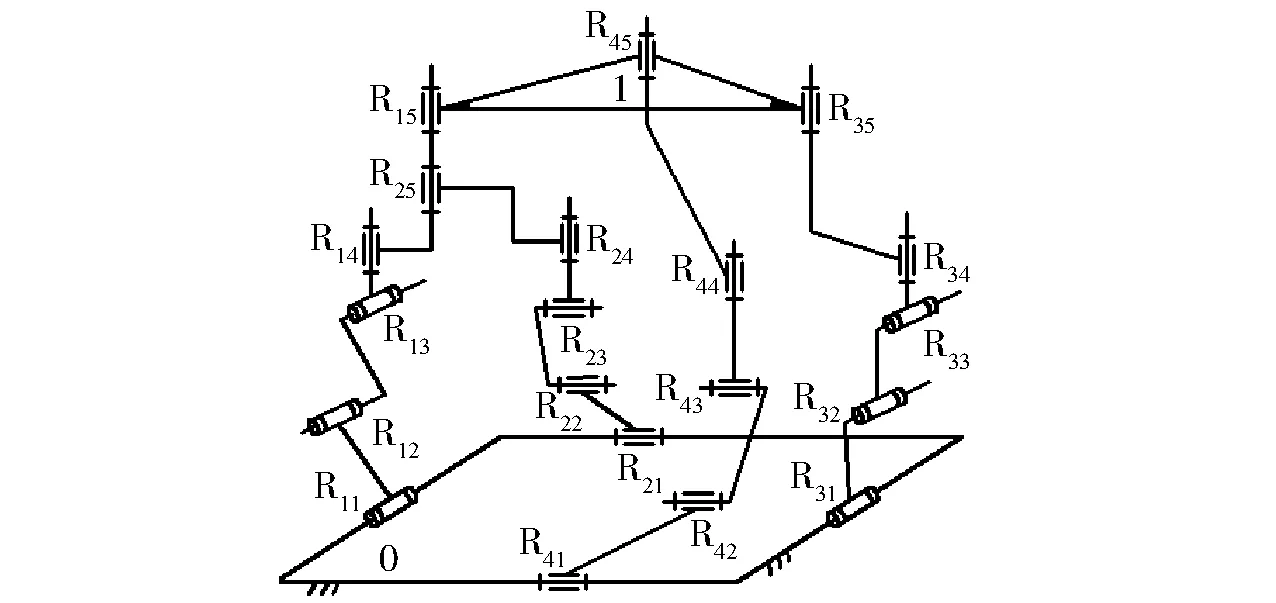
图10 一次降耦后的I型3T1R机构Fig.10 Once decoupled type Ⅰ 3T1R parallel mechanism

(1)确定第1回路及其约束度Δ1

loop1{-R11‖R12‖R13⊥R14‖R25‖R24⊥

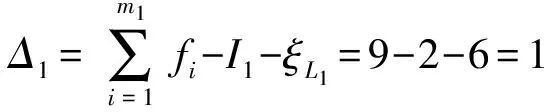
(2)确定第2回路及其约束度Δ2

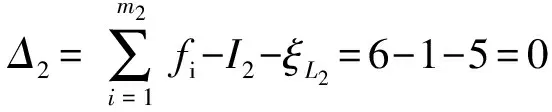
(3)确定第3回路及其约束度Δ3

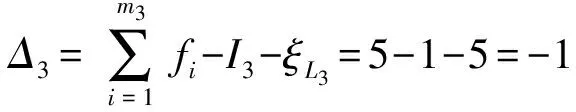
(4)机构的耦合度κ

因此，降耦后的机构仍由一个BKC组成，但其耦合度已降为κ=1。

进一步，对图10所示机构中另2条垂直配置的支链在动平台1上的转动副R35和R45重合(称为：二次降耦)，则形成第2条含空间回路的复杂支链，得到如图11所示的机构[32]，其耦合度计算为：

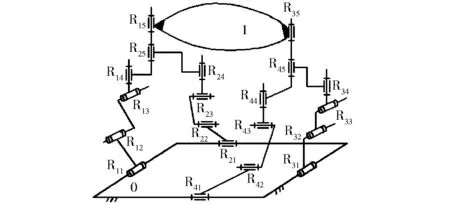
图11 二次降耦后的I型3T1R机构Fig.11 Twice decoupled type Ⅰ3T1R parallel mechanism

(1)确定第1回路及其约束度Δ1

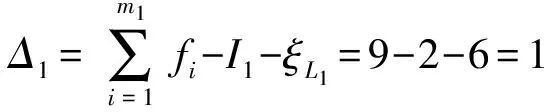
(2)确定第2回路及其约束度Δ2

根据基于约束度Δ最小的回路选择原则[2]，第2回路不应选复杂支链2构成的回路(其约束度为1)，而应为

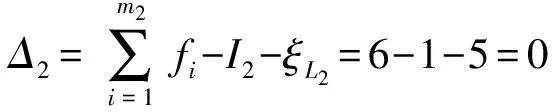
(3)确定第3回路及其约束度Δ3

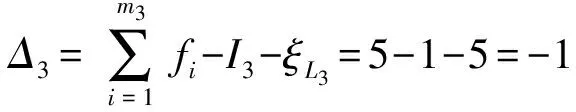
(4)机构的耦合度κ

因此，该机构仍含1个BKC，其耦合度也已降为κ=1；但机构的自由度为F=4，过约束数Nov.=2，POC集为三平移一转动，仍没有改变。

需要说明的是：图1所示Ⅰ型3T1R机构的动平台1和支链有4个转动副连接，而图10、11所示机构的动平台1和支链连接的转动副，分别减少为3、2个，也许会增大动平台的工作灵活性和工作空间，这有待详细分析。

3.2 Ⅱ型 3T1R并联机构的降耦设计

将图2所示Ⅱ型 3T1R并联机构中，垂直配置的2条支链在动平台1上的转动副R15和R35重合(一次降耦)，则得到如图12所示的降耦机构[31]，其耦合度计算如下：

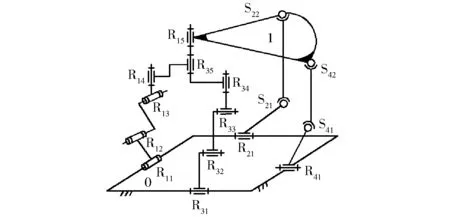
图12 一次降耦后的Ⅱ型3T1R机构Fig.12 Once decoupled type Ⅱ 3T1R parallel mechanism

(1)确定第1回路及其约束度Δ1，同图10所示机构，为

loop1{-R11‖R12‖R13⊥R14‖R35‖R34⊥R33
‖R32‖R31-}

(2)确定第2回路及其约束度Δ2

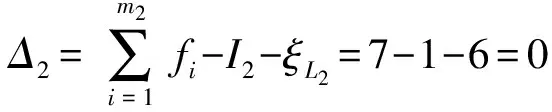
(3)确定第3回路及其约束度Δ3

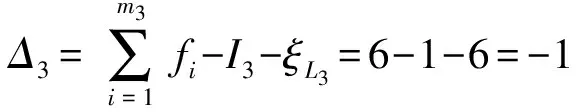
(4)机构耦合度κ

因此，该机构仅含1个BKC，其耦合度已降为1。进一步，将图12所示机构的其它2条S-S-R无约束支链在动平台1上的球副S22和S42重合(二次降耦)，形成第2条含空间回路的复杂支链，得到图13所示的机构[31]，同样有：

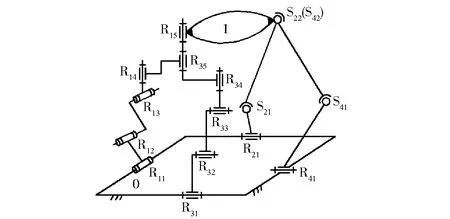
图13 二次降耦后的Ⅱ型3T1R机构Fig.13 Twice decoupled type Ⅱ 3T1R parallel mechanism

(1)确定第1回路及其约束度Δ1，同上，为

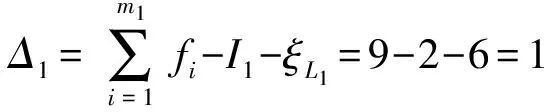
(2)确定第2回路及其约束度Δ2，同上，为

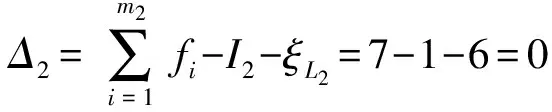
(3)确定第3回路及其约束度Δ3

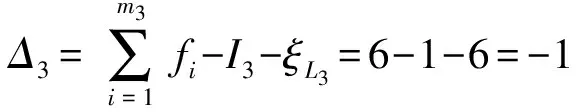
(4)机构耦合度κ

即该机构耦合度已降为κ=1，显然，机构的位置正解以及动力学分析较为容易，但机构的POC和自由度(F=4)都没变，但简化了机构的结构。其复合的球副可采用文献[33]提出的“易制造结构”来设计与制造，如图14所示。

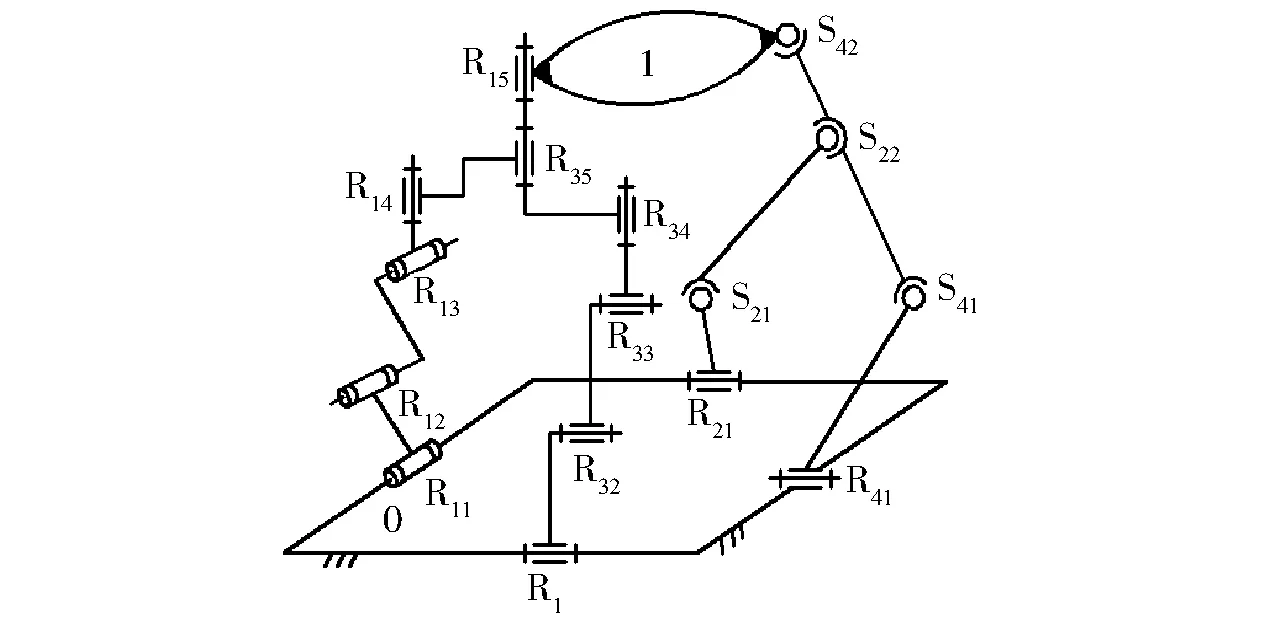
图14 二次降耦后的Ⅱ型3T1R机构易制造结构Fig.14 Twice decoupled type Ⅱ 3T1R parallel mechanism (easy fabrication structure)

其他5种3T1R机构的降耦设计，可同样处理，限于篇幅，从略。

这样，共得到14个低耦合度(κ=1)机型，其

中，动平台具有3个运动副的有7个，另7个为动平台具有2个运动副。这样，7个耦合度较大的(κ=2)以及14个低耦合度(κ=1)的4-DOF 3T1R原创性新机构，构成了可实现SCARA运动的机构库，为其进一步研究、优选、设计与应用奠定了良好的理论基础。

4 结论

(1)根据基于方位特征(POC)和序单开链(SOC)的并联机构拓扑结构设计理论与方法，对提出的一类7个具有较好实用价值的SCARA并联机构，进行了拓扑结构分析，揭示了其POC集、自由度(含驱动副选取)、Nov.、耦合度、I-O解耦性等5个最主要的拓扑特征，发现其耦合度均较大为κ=2，表明其运动学位置正解和动力学求解十分复杂。

(2)基于结构降耦原理，继而又对上述κ=2的这7个机构，通过动平台上转动副或球副的复合，进行了拓扑结构降耦优化，又得到了14个结构更简单、耦合度更低(κ=1)而POC、DOF等保持不变的3T1R原创性机构，一方面，它们的运动学正解及动力学正反解的代数求解难度大大降低，其数值解可用一维搜索法方便求得；另一方面，大大丰富了SCARA并联机构库，为SCARA并联机构类型优选、运动学与动力学综合和分析，以及设计和应用提供了基础。

(3)分析并揭示并联机构的方位特征集(POC集)及其维数、独立回路数v、独立位移方程数ξLi、过约束数Nov.、自由度(DOF)类型和数目F、基本运动链(BKC)类型及其数目、BKC耦合度κ、I-O解耦性、消极运动副、驱动副选择、冗余度等12个指标，它能为并联机构类型优选及其性能评价提供重要依据，为机构的优选、运动学与动力学的求解提供明确的方向，可在机构选型阶段就能大致了解机构的一些运动学和动力学性能，大大减少机构创新设计阶段反复、冗长的运动学和动力学综合、分析复杂性及其计算时间，因此，机构的拓扑结构特征分析，应为并联机构研究与开发应用中的一个重要环节。

1 杨廷力．机器人机构拓扑结构学[M]．北京：机械工业出版社，2004．

2 杨廷力，刘安心，罗玉峰，等．机器人机构拓扑结构设计[M]．北京：科学出版社，2012．

3 HUANG Z，LI Q C．Type synthesis of symmetrical lower-mobility parallel mechanisms using the constraint-synthesis method [J]．The International Journal of Robotics Research，2003，22(1)：59-79．

4 高峰，杨加伦，葛巧德．并联机器人型综合的GF集理论[M]． 北京：科学出版社，2011．

5 KONG X, GOSSELIN C M. Type synthesis of parallel mechanisms[M].Berlin Heidelberg：Springer，2007：45-53．

6 HERVE J M．Analyse structurelle des mecanismes par groupe de deplacements [J]．Mechanism and Machine Theory，1978，13(4):437-450．

7 GOUGU G．Structural synthesis of parallel robots．Part 1：Methodology[M]．Berlin Heidelberg: Springer, 2008．

8 ABB．IRB 360 Flexpicker[EB/OL]．[2015-05-06]http：∥www.new.abb.com/products/robotics /industrials-robots/irb-360．

9 CLAVEL R．Device for the movement and positioning of an element in space：US，4976582[P]．1990-12-11．

10 PIERROT F，COMPANY O．H4：a new family of 4-DOF parallel robots[C]∥Proceedings of the IEEE/ASME International Conference on Advanced Intelligent Mechatronics，1999：508-513.

11 KRUT S，COMPANY O，BENOIT M，et al. I4：a new parallel mechanism for SCARA motions[C]∥Proceedings of the IEEE International Conference on Robotics and Automation，2003：1875-1880.

12 NABAT V，COMPANY O，KRUT S，et al. Par4：very high speed parallel robot for pick-and-place[C]∥Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems，2005：1202-1207.

13 赵铁石，黄真．欠秩空间并联机器人输入选取的理论和应用[J]．机械工程学报，2000，36(10)：81-85．

ZHAO Tieshi，HUANG Zhen．Theory and application of selecting actuating components of spatial parallel mechanisms[J]．Chinese Journal of Mechanical Engineering，2000，36(10)：81-85．(in Chinese)

14 金琼，杨廷力，刘安心，等．基于单开链单元的三平移一转动并联机器人机构型综合及机构分类[J]．中国机械工程，2001，12(9)：1038-1043．

JIN Qiong, YANG Tingli, LIU Anxin, et al. Structural synthesis and classification of the 3-DOF translational parallel robot mechanism based on the units of single-opened-chain[J]. Chinese Journal of Mechanical Engineering, 2001, 12(9): 1038-1043．(in Chinese)

15 杨廷力，金琼，罗玉峰，等．用于虚轴机床与机器人等的一类(三平移一转动)并联机构：CN,1528568[P].2004-09-15．

16 黄田，刘海涛，李曚．五自由度机器人：CN，1709657 [P]．2005-08-21．

17 刘辛军，谢福贵，王立平，等．一种可实现SCARA运动的四自由度单动平台并联机构:CN，201210435375．1[P]．2012-11-02．

18 XIE F G，LIU X J．Design and development of a high-speed and high-rotation robot with four identical arms and a single platform[J]. Journal of Mechanisms amp; Robotics，2015，7(4)：041015．

19 沈惠平，杨廷力，孟庆梅，等．一种三平移一转动并联机器人操作手:CN,201510564195．7 [P].2015-09-08．

20 沈惠平，杨廷力，李菊，等．一种三平移一转动并联机器人装置:CN,201510567133．1 [P].2015-09-08．

21 沈惠平，杨廷力，邓嘉鸣，等．一种三平移一转动并联机器人机构:CN,201510566039．4 [P].2015-09-08．

22 沈惠平，杨廷力，邵国伟，等．一种三平移一转动并联机构机械手:CN,201510640394．X [P]. 2015-10-09．

23 沈惠平，杨廷力，李云峰，等．一种三平移一转动并联机器人抓放器:CN,201510648948．2 [P].2015-10-09．

24 沈惠平，杨廷力，朱伟，等．一种三平移一转动并联机器人平台:CN,201510566840．9 [P]. 2015-09-08．

25 沈惠平，杨廷力，朱小蓉，等．一种三平移一转动并联机器人:CN,201510564382．5 [P]. 2015-09-08．

26 沈惠平，尹洪波，李菊，等．基于方位特征方法的范例并联机构的拓扑特征分析及其启示与应用[J]．机械工程学报，2015，51(13) ：101-115．

SHEN Huiping，YIN Hongbo，LI Ju，et al．Position and orientation characteristic based method and enlightenment for topology characteristic analysis of typical parallel mechanisms and its application[J]．Journal of Mechanical Engineering，2015，51(13)：101-115．(in Chinese)

27 SHEN Huiping，YANG Liangjie，MENG Qingmei，et al．Topological structure coupling-reducing of parallel mechanisms[C]∥2015 Iftomm World Congress，2015．

28 沈惠平，朱小蓉，尹洪波，等．并联机构的结构降耦原理及其设计方法研究[J]．机械工程学报，2016，52(23)：102-113．

SHEN Huiping，ZHU Xiaorong，YIN Hongbo，et al．Study on the principle and design method for structure coupling-reducing of parallel mechanisms[J]．Journal of Mechanical Engineering，2016，52(23)：102-113．(in Chinese)

29 沈惠平，熊坤，孟庆梅，等．并联机构运动解耦设计方法与应用研究[J/OL]．农业机械学报，2016，47(6)：348-356．http:∥www.j-csam.org /jcsam/ch/reader/view_abstract.aspx?flag=1amp;file_no=20160646amp;journal_id=jcsam. DOI：10.6041 /j.issn.1000-1298.2016.06.046.

SHEN Huiping，XIONG Kun，MENG Qingmei，et al．Principle，design method and novel configurations for decoupled parallel mechanisms[J/OL]．Transactions of the Chinese Society for Agricultural Machinery，2016，47(6)：348-356.(in Chinese)

30 尹洪波，沈惠平，邓嘉鸣，等．球面并联机构的结构降耦及其位置正解求解[J]．机械科学与技术，2015，34(1)：51-55．

YIN Hongbo，SHEN Huiping，DENG Jiaming，et al．The reducing in structure coupling and forward position analysis for the spherical parallel mechanism[J]．Mechanical Science and Technology for Aerospace Engineering，2015，34(1)：51-55．(in Chinese)

31 沈惠平，朱伟，曾氢菲，等．一种低耦合度三运动副动平台的三平移一转动并联机器人操作手:CN,201610141778.3[P]. 2016-03-15．

32 沈惠平，孙驰宇，杨廷力，等．一种低耦合度两运动副动平台的三平移一转动并联机器人操作手:CN,201610140160.5[P]. 2016-03-15．

33 YU Tongzhu，SHEN Huiping．An easily manufactured structure and its analytic solutions for forward and inverse position of 1-2-3-SPS type 6-DOF basic parallel mechanism[C]∥Proceedings of the 2012 IEEE International Conference on Robotics and Biomimetics，2012：1194-1199．

TopologicalAnalysisforFamilyofSCARAParallelMechanismsandTheirEquivalentDesignwithLowCouplingDegree

LI Ju ZENG Qingfei SHEN Huiping YANG Tingli

(ResearchCenterforAdvancedMechanismTheory,ChangzhouUniversity,Changzhou213016,China)

According to the parallel mechanism design theory and systematical method based on position and orientation characteristic (POC), a total topological structures analysis was performed on seven typical new SCARA parallel mechanisms (PMs) with proposed practical value. Five major topological features were revealed, which were POC set, degree of freedom (including the selection of drive pair), over-constraint degree, coupling degree and input-output motion decoupling relationship of PMs. It was found that the coupling degree of these PMs were bigger withκ=2, which meant that the forward kinematics solutions and inverse dynamic solution of the PMs were very complete. Therefore, decoupling and optimization of these PMs were completed based on the proposed mechanism topological structural decoupling principles, and 14 new equivalent mechanisms with lower coupling degree which had the same POC and DOF were achieved. Thus the 4-DOF mechanism with three translations and one rotation which can achieve Schonflies motion can be enriched greatly, and the forward kinematics solutions and inverse dynamic solution of these PMs can be obtained easily, and the numerical solution can be gotten conveniently by using one dimensional searching method. The research provided a theoretical basis for the kinematics synthesis and analysis, design and applications for these new SCARA PMs.

parallel mechanism; POC method; topological structure analysis; coupling degree; topological characteristics; mechanism synthesis

10.6041/j.issn.1000-1298.2017.11.050

TH112

A

1000-1298(2017)11-0405-12

2017-03-12

2017-04-10

国家自然科学基金项目(51405039、51375062、51475050)、江苏省重点研发计划项目(BE2015043)和江苏省科技成果转化专项资金项目(BA2015098)

李菊(1981—)，女，讲师，博士，主要从事机器人机构设计和自动控制研究，E-mail: wangju0209@163.com