一种基于主成分分析的协同克里金插值方法

卢月明，王 亮，仇阿根，张用川,2，赵阳阳

(1. 中国测绘科学研究院, 北京 100830； 2. 武汉大学资源与环境科学学院，湖北 武汉 430079)

一种基于主成分分析的协同克里金插值方法

卢月明1，王 亮1，仇阿根1，张用川1,2，赵阳阳1

(1. 中国测绘科学研究院, 北京 100830； 2. 武汉大学资源与环境科学学院，湖北 武汉 430079)

针对协同克里金插值方法在插值时，辅助变量较多造成计算复杂度增加，而辅助变量较少引起插值精度降低这一问题，提出了一种基于主成分分析的协同克里金插值方法(PCA-CoKriging)。该方法首先使用主成分分析对插值相关变量进行将维，得到较少几个综合指标，然后里利用这几个综合指标作为辅助变量进行协同克里金插值。为验证该方法的有效性和数据分布对该方法的影响，本文选取了2016年北京市范围内4个季节中PM2.5浓度满足正态分布效果不同的4组数据，分别使用PCA-CoKriging和普通克里金插值方法、常规协同克里金插值方法，进行了插值试验。结果表明，本文方法与普通克里金插值方法、常规协同克里金插值法在4组试验中的平均绝对误差分别为4.91、6.04、5.61，平均均方根误差分别为6.65、8.76、7.57。综合比较，本文方法比常规协同克里金插值的平均绝对误差与均方根误差分别提升了10.73%、12.56%，比普通克里金插值法的平均绝对误差与均方根误差分别提升了18.71%、24.09%。

主成分分析；协同克里金插值；Pearson相关系数；PM2.5

随着经济的快速发展，大气污染也急速加剧，其中大气颗粒物是导致大气污染的主要原因[1-2]。以PM2.5为主的颗粒污染物不仅导致大气能见度降低[3-4]，还会影响人的身体健康[5-6]，因此引起了人们的广泛关注。对PM2.5等颗粒污染物的空间分布进行研究，可获取各区域颗粒物的分布情况，为分析其污染空间变化趋势提供参考依据。空间插值是计算大气环境组成要素数值的有效方法，常用于将离散点数据转换为连续曲面，以便直观地考察数据要素的空间分布模式[7]。

普通克里金插值方法综合考虑了空间异质性和依赖性，其最优无偏特性在模型的模拟与预测方面得到了较好的体现[8]。因此，普通克里金插值法在大气污染、PM2.5浓度预测等方面得到了广泛的应用[9-12]。但普通克里金插值方法只能单一进行PM2.5浓度的空间预测与模拟，并不能考虑众多相关变量的影响。对此，彭彬[13]、王平[14]等对协同克里金插值方法进行了深入研究，研究表明协同克里金插值法不仅考虑了变量的空间连续性，还考虑了变量之间的相关关系；姜勇[15]、范晓梅[16]等研究证明协同克里金插值方法可以缩小极值误差范围、降低均方根误差，还可以提高实测值与预测值的拟合精度。而利用协同克里金插值法的关键在于辅助变量的选取。郭龙[17]、赵彦锋[18]等研究表明在选取辅助变量时单一地选取与目标变量相关性较高的因素，不能全面地反映辅助变量的信息。在实际应用中，影响PM2.5浓度的因素有很多[19-21]，直接进行协同克里金插值，会极大地降低插值模型的运算效率。章清[22]等研究表明利用主成分分析法可以在较多的影响因素中去除数据的冗余和共线性，提取有价值的信息构建新的变量，并将其作为协同变量插值可得到更优的插值效果；张崇甫[23]、王晓鹏[24]等研究指出传统主成分分析法存在两个明显的不足：一是综合评价的实际结果与评价指标间的相关程度高低成正比，评价指标间相关程度越高，主成分分析的结果越好。当指标间的相关性小时，每一个主成分承载的信息量就少，为满足累积方差贡献率达到一定水平(通常为85%以上)，可能需要选取较多的主成分，这样主成分分析法的降维效果不明显。二是主成分分析是一种线性降维方法，只能处理线性问题。

因此，本文针对协同克里金插值时，辅助变量较多时计算复杂度高，而辅助变量较少时插值精度低这一问题，提出了一种基于主成分分析的协同克里金插值方法(PCA-CoKriging)。该方法首先采用非线性主成分分析方法(nonlinear principal component analysis，NPCA)对影响PM2.5浓度的若干指标进行降维得到几个综合指标，并将其作为协同克里金插值的辅助变量。为验证该方法的有效性，利用Pearson相关系数法选取与PM2.5浓度具有较高相关性的影响因素作为辅助变量，在辅助变量个数相同的前提下，与本文方法进行对比。本文以平均绝对误差(mean absolute error，MAE)、均方根误差(root mean square error，RMSE)作为评价指标来说明模型的准确性。

1 研究方法

1.1 非线性主成分分析原理

在实际问题中，经常遇到研究多个变量的问题，而且在多数情况下，多个变量之间常常存在一定的相关性。由于变量个数较多，再加上变量之间的相关性，势必会增加分析问题的复杂性。实际应用时，主成分分析法可以将多个变量综合为少数几个代表性变量，既能代表原始变量的绝大多数信息，又互不相关，可以使用新的综合变量作进一步的统计分析。

主成分分析法利用降维的思想，把原来较多的评价指标用较少的综合主成分指标代替，通过对原始数据的变换和处理，综合指标不仅保留了原始影响因素的主要信息，而且各个因素之间的相关性也得以弱化，从而使复杂问题简单化[25]。因此，在进行协同克里金法空间插值前使用主成分分析方法对若干相关指标进行分析，得到几个综合指标，并使用这几个综合指标作为协同指标进行空间插值。但是传统的主成分分析方法存在两个不足之处：一是综合评价的实际结果与评价指标间的相关程度高低成正比，评价指标间相关程度越高，主成分分析的结果越好。当指标间的相关性小时，每一个主成分承载的信息量就少，为满足累积方差贡献率达到一定水平(通常为85%以上)，可能需要选取较多的主成分，这样主成分分析法的降维效果不明显。二是主成分分析是一种线性降维方法，只能处理线性问题[23-24]。

研究实际问题时，不仅指标间有非线性关系，而且有时主成分与原始数据之间也呈非线性关系，如果简单地进行线性处理，必然导致评价结果的偏差。因此有必要对传统主成分的“线性化”进行改进。针对此问题，本文运用非线性主成分分析法，对影响PM2.5浓度的相关指标进行分析，从而得到几个主成分，将其作为协同克里金插值法的协同变量。

设有p维向量x=(x1,x2,…,xp)的样本资料(xij)n×p，算法步骤如下：

(1) 对原始数据作中心化对数比变换

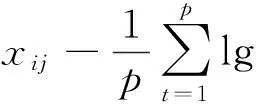
(2) 计算中心化对数比样本协方差矩阵

S=(Sij)p×p

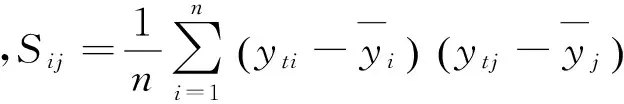
(3) 从S出发求样本主成分。设λ1>λ2…>λp是S的p个特征根，(a1,a2,…,ap)是相应的标准化特征向量，则第i个主成分为

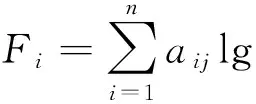
非线性主成分分析与传统的主成分分析相比有两处改进：一是通过对原始数据作对数中心化变换，将主成分表示为原始数据的非线性组合；二是分析的出发点是协方差矩阵，而不是相关系数矩阵。通过这两处改进，可明显提高降维效果，用更少的主成分反映更多的原始指标的信息，并且评价的稳定性与合理性也有所提高。

1.2 协同克里金插值模型

克里金插值法是以变异函数理论和结构分析为基础，在有限区域内对区域化变量进行无偏最优估计的一种方法。协同克里金法(CoKriging)是对普通克里金法的一种扩展应用，它利用多种变量类型，将主变量的自相关性和协变量的交叉相关性结合起来用于无偏最优估计中[26]。其优点是当主变量难以获得或获取代价很高时，协同克里金法采用更易获取或样本分布密度很高，且与主变量有一定的相关性的辅助变量对主变量进行预测，从而提高插值精度[27]。研究表明，当主辅变量间的相关性超过0.45的中等程度时，协同克里金法的插值精度明显优于普通克里金法[14]。

协同克里金法的表达式为

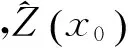
1.3 基于非线性主成分分析的协同克里金插值原理

本文尝试将非线性主成分分析法与协同克里金插值法结合，充分利用非线性主成分分析的降维与协同克里金插值的空间分析能力，对北京市PM2.5浓度进行空间插值。即在协同克里金插值之前，利用非线性主成分分析法进行预处理，将与主变量相关的众多影响因素降维得到少数的几个综合指标，然后再使用这几个综合指标作为辅助变量进行插值。该方法有效地解决了当主变量的影响因素较多时，ArcGIS中CoKriging不能充分考虑的问题(辅助变量最多为3个)，且降维得到的几个综合指标包含了原来变量的绝大多数信息，降低了信息的损失，同时也弥补了传统主成分分析法只能处理线性问题的不足。

基于非线性主成分分析的协同克里金插值流程如下：

(1) 对原始数据进行非线性主成分分析变换得到反映原始相关变量的几个综合指标，截取累积贡献度超过85%的前几个综合指标。

(2) 使用这几个综合指标作为协同克里金插值的辅助变量，进行空间插值。

(3) 计算该模型的评价指标，并与其他方法对比，验证该模型的插值结果。

2 插值试验

2.1 研究区概况

北京位于东经115.7°—117.4°，北纬39.4°—41.6°，中心位于北纬39°54′20″，东经116°25′29″，总面积达16 410.54 km2，全市常住人口达2100多万人，是中国的首都、政治中心、文化中心、科技创新中心。近年来，以PM2.5和PM10为主的大气颗粒物浓度急剧升高，导致北京的雾霾天频发，以致频频启动“重雾霾橙色预警”。北京市政府也启动了多项措施来应对重污染天气。

2.2 数据来源

本文中选取北京2016年1月、4月、7月、10月等处在不同季节的35个监测站点每小时监测数据(包括PM2.5、PM10、NO2、CO、SO2、O3等大气污染物的浓度数据)和每个监测站点的经度与纬度，上述监测数据抓取自网站www.pm25.in。北京市环境保护监测中心建立的城市空气质量实时监测网络共包括35个自动监测站点，遍布北京城六区及其十郊县，其覆盖范围基本可以反映整个北京地区的空气质量状况，监测站点分布如图1所示。

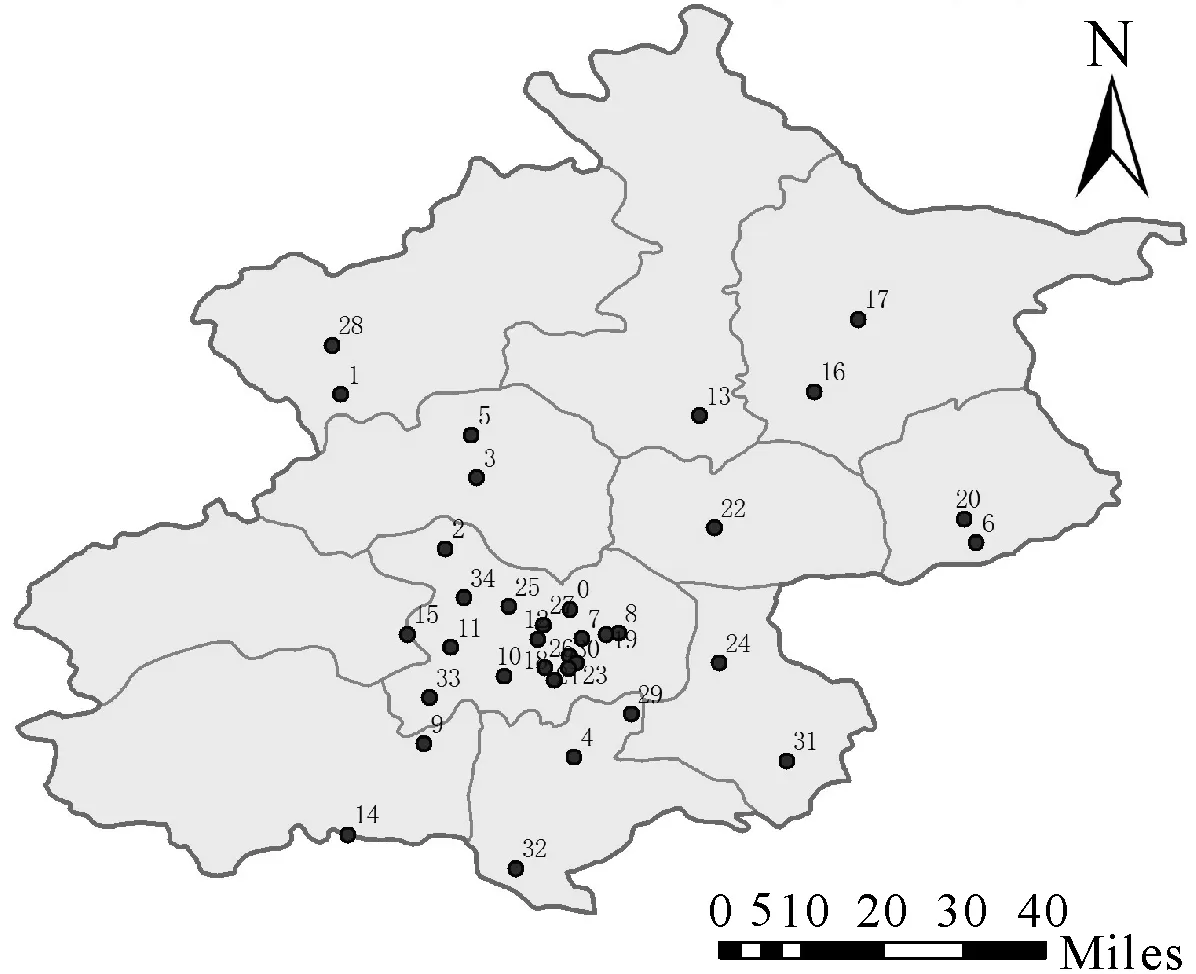
图1 北京地区空气质量监测站点分布

2.3 数据预处理

2.3.1 数据分布检验

在获取样本点数据后，首先需要对数据进行分析，检验数据的分布，分析数据的趋势等，探索性空间数据分析(explore spatial data analyst,ESDA)模块提供了一系列的工具来检查数据，以便对数据相关问题做出更加合理、科学的决策。在地统计分析中，克里金插值是建立在平稳假设的基础上，这种假设在一定程度上要求所有数据具有相同的变异性。另外，克里金插值还假设数据服从正态分布。如果数据不服从正态分布，需要进行一定的数据变换，从而使其服从正态分布。因此，在进行地统计分析前，检验数据的分布特征，了解和认识数据具有非常重要的意义。本文采用直方图来检验数据的分布特征，如图2—图5所示。

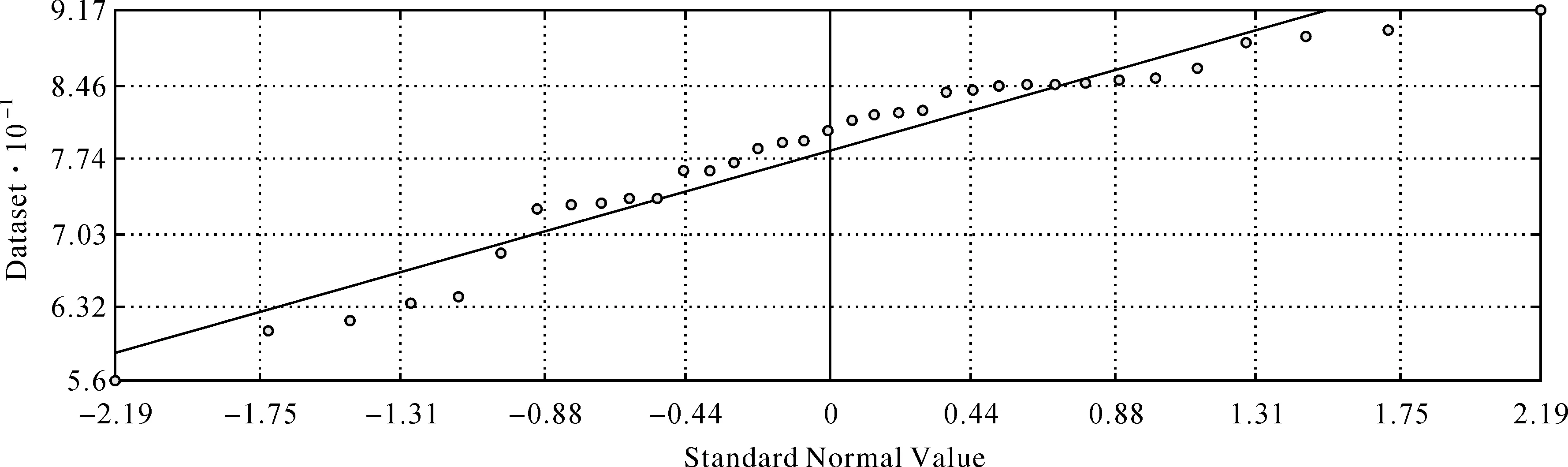
图2 1月PM2.5数据QQPlot图

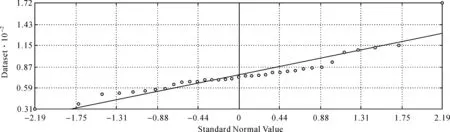
图3 4月PM2.5数据QQPlot图

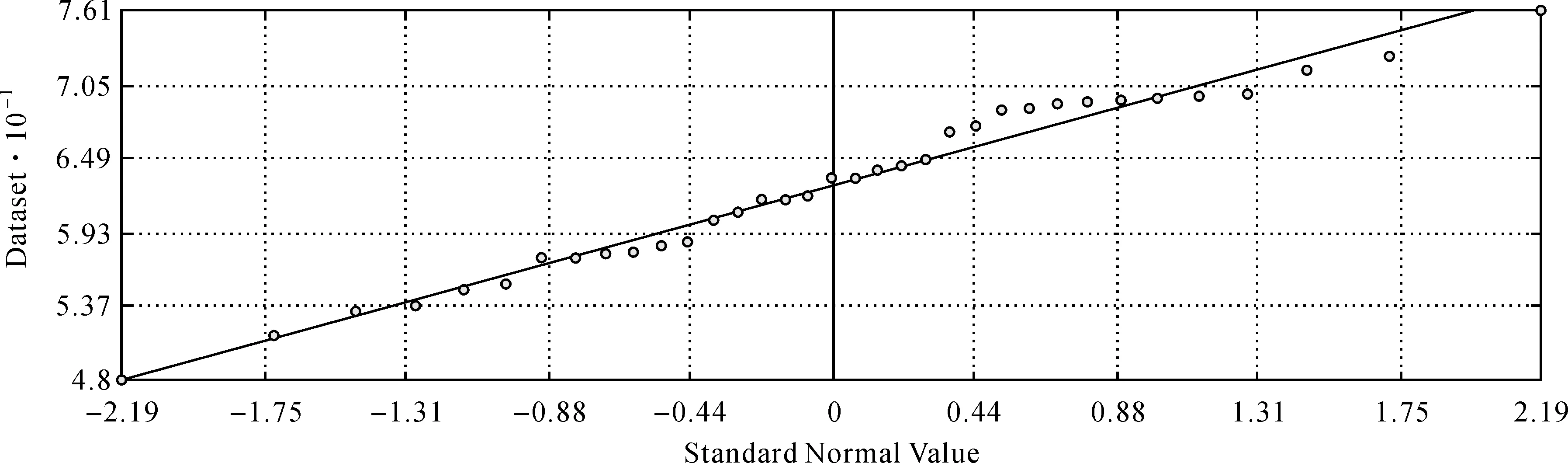
图4 7月PM2.5数据QQPlot图

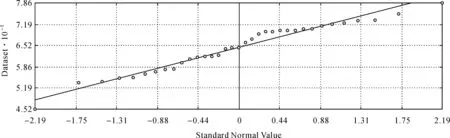
图5 10月PM2.5数据QQPlot图

由图2—图5可看出，4月、7月、10月的数据的正态分布校验效果较好，1月的数据正态分布校验结果较差，但基本满足正态分布假设。

2.3.2 指标间相关性检验

指标间存在相关性是进行主成分分析的必要前提。因此，在进行非线性主成分分析前，先对各个指标进行相关性检验，本文是计算各个指标的Pearson相关系数，结果见表1。由表1可看出，SO2、CO、NO2与PM2.5呈显著正相关，其中，O3与PM2.5呈负相关，PM10与PM2.5在1月、4月和7月相关性较弱(以下数据均保留5位小数)。

表1 Pearson相关系数表

2.3.3 非线性主成分分析

根据前文非线性主成分分析原理计算得到各个月份的特征值及其相应的贡献度，以及累积贡献度见表2(以下数据均保留5位小数)。

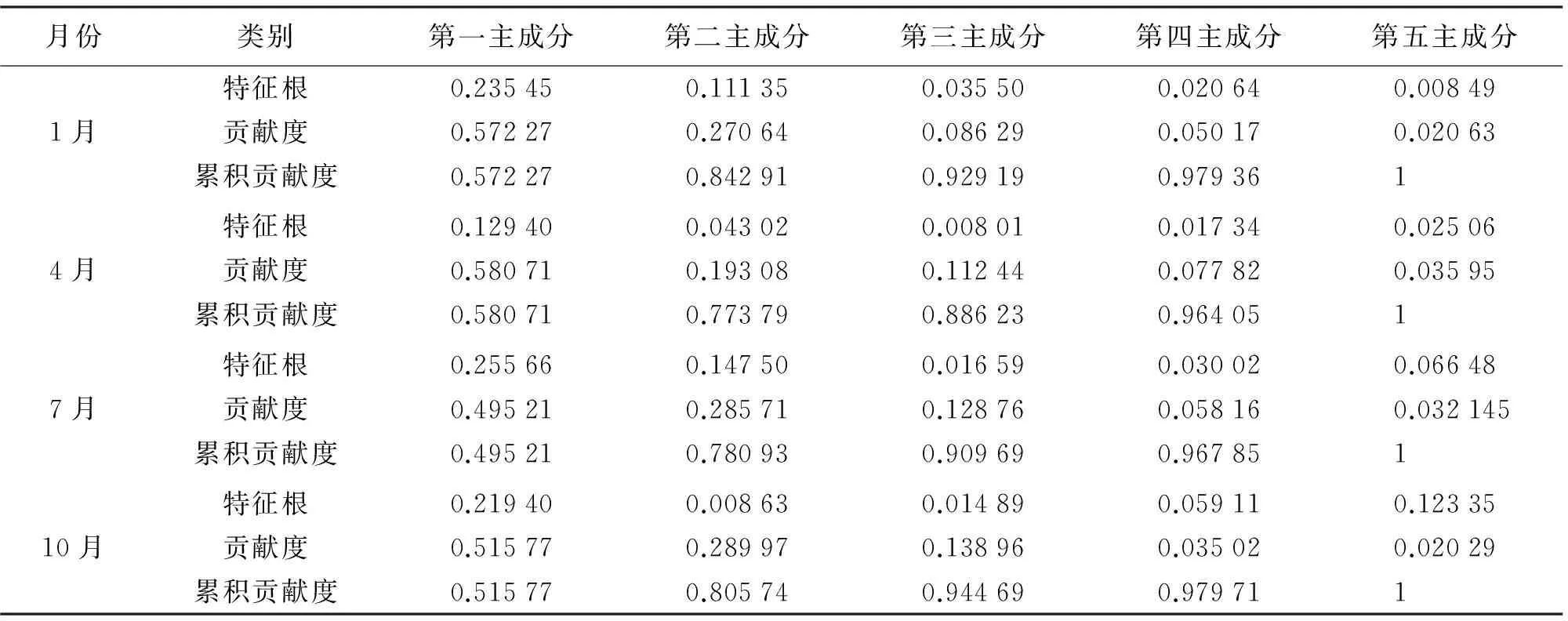
表2 非线性主成分分析结果

由表2可知，各个月份的第一主成分贡献度均在50%左右，前3个主成分的累积贡献度只有4月在88.6%，未超过90%，其余3个月的累积贡献度均超过90%，其中10月的更是高达94.4%。因此，本文采用前3个主成分作为协同克里金法的辅助变量进行空间插值。

3 结果与分析

3.1 插值结果分析

为了评估本文研究方法的插值效果，本文将其与协同克里金方法进行对比，协同克里金的辅助变量为与主变量相关系数最高的前3个变量：SO2、CO、NO2，通过交叉验证计算各个方法的平均绝对误差(MAE)、均方根误差(RMSE)[28]，并将其作为插值结果的评价指标来对两种方法的插值结果进行评估。其中平均绝对误差反映估计值可能的误差范围，均方根误差反映插值函数的灵敏度和极值效应，这两个指标均是越小代表精度越高。经计算，得到两种插值方法的插值精度与精度提升百分比，见表3、表4(CoKriging代表使用原指标进行协同克里金插值，PCA-CoKriging代表使用非线性主成分分析处理的综合指标进行插值)。

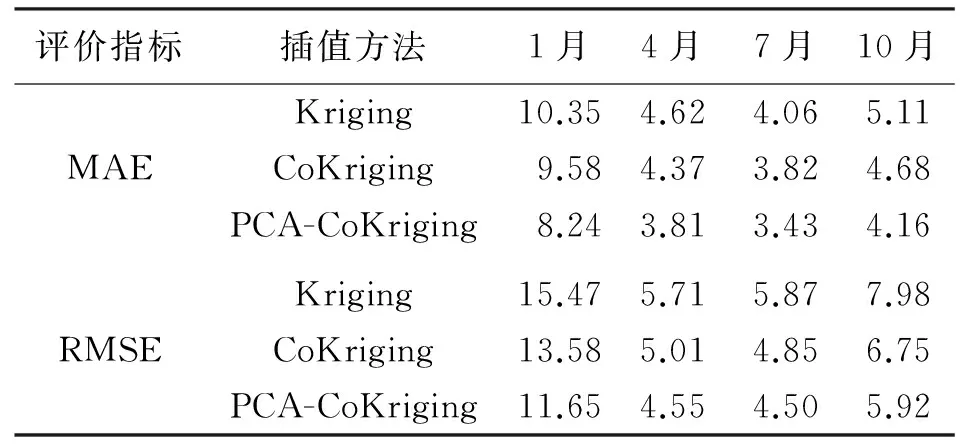
表3 插值精度对比

表4 插值精度提升百分比

由表3、表4可知，1月的误差较大，主要是由于1月的数据正态分布检验结果较差。PCA-CoKriging法相对于CoKriging法、Kriging法，MAE和RMSE都有一定程度的改善。其中相对于CoKriging法，CoKriging(NPCA)法的MAE的提升度均在10%之上，1月、10月的RMSE提升度也在10%之上，4月、7月的RMSE较低分别为9.18%和7.21%。相对于Kriging法，PCA-CoKriging法的提升程度更高，MAE的提升度均在15%以上，1月的MAE更是提升了20.38%，而RMSE的提升度均在20%以上，充分说明了相同辅助变量个数的前提下PCA-CoKriging法的优势。

从以上两表也可看出考虑影响因素的CoKriging法较之未考虑的Kriging法，也有明显的改善，MAE均在5%以上，RMSE均在12%以上，验证了文献[8]的结论：在当主辅变量间的互相关性超过0.45的中等程度时，协同克里金法的插值精度明显优于普通克里金法。

3.2 协同克里金插值结果

本文采用ArcGIS进行协同克里金插值作图，但在ArcGIS中作协同克里金插值的辅助变量最多为3个，如果要考虑更多的辅助变量，ArcGIS便无能为力。这时就可采用本文的方法，对原始变量进行预处理得到少数几个综合指标，然后再使用ArcGIS进行插值即可。利用非线性主成分分析得到的综合指标进行协同克里金插值结果如图6—图9所示。

4 结 论

上述结果表明，在相同辅助变量的前提下使用非线性主成分分析得到的综合指标作为辅助变量进行协同克里金插值，精度有明显的提升，说明该方法不仅可以有效地降低计算工作量，减少原始数据信息损失，简化数据结构，还消除了各个影响因素之间的共线性，提高了插值精度。

(1) 相关分析得出SO2、CO、NO2与PM2.5呈正相关，O3与PM2.5呈负相关，SO2、CO、NO2、O3、PM10与PM2.54个月的平均相关性大小依次为NO2>CO>SO2>O3>PM10，其中NO2、CO、SO2与PM2.5的相关性均大于0.45。

(2) 插值结果表明，本文采用非线性主成分分析处理后的综合指标进行协同克里金插值的插值精度较高，且减小了计算量，提高了运算效率，经过对比该方法的平均绝对误差与均方根误差均低于常用的协同克里金插值法，4个月的平均绝对误差与均方根误差平均提升度分别为10.73%、12.56%。但本文方法也受数据分布的影响，但数据较好地满足正态分布时，插值精度较高，反之，插值精度较差。

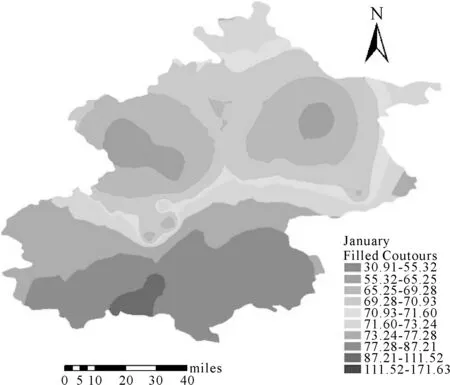
图6 1月PM2.5插值图

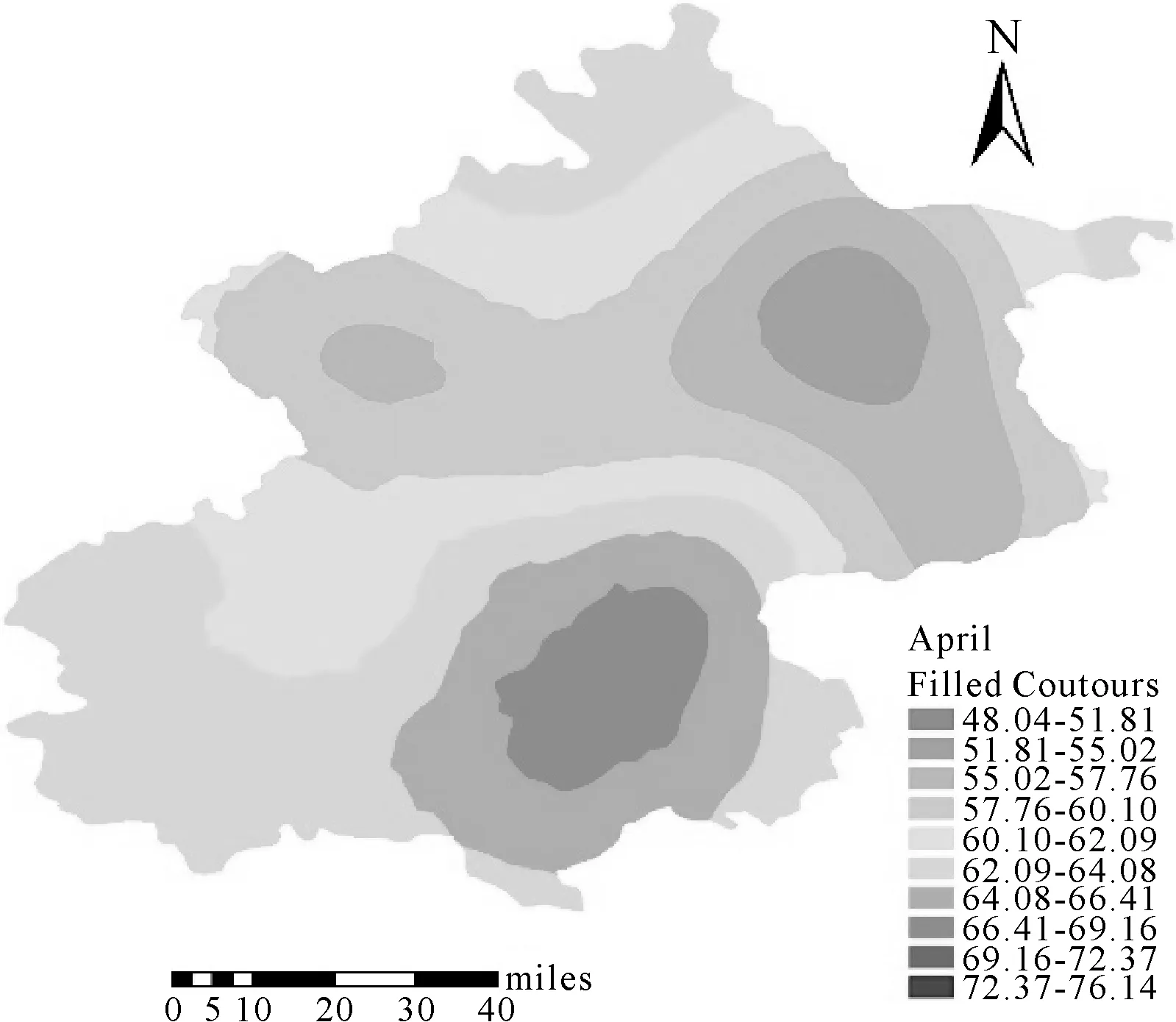
图7 4月PM2.5插值图

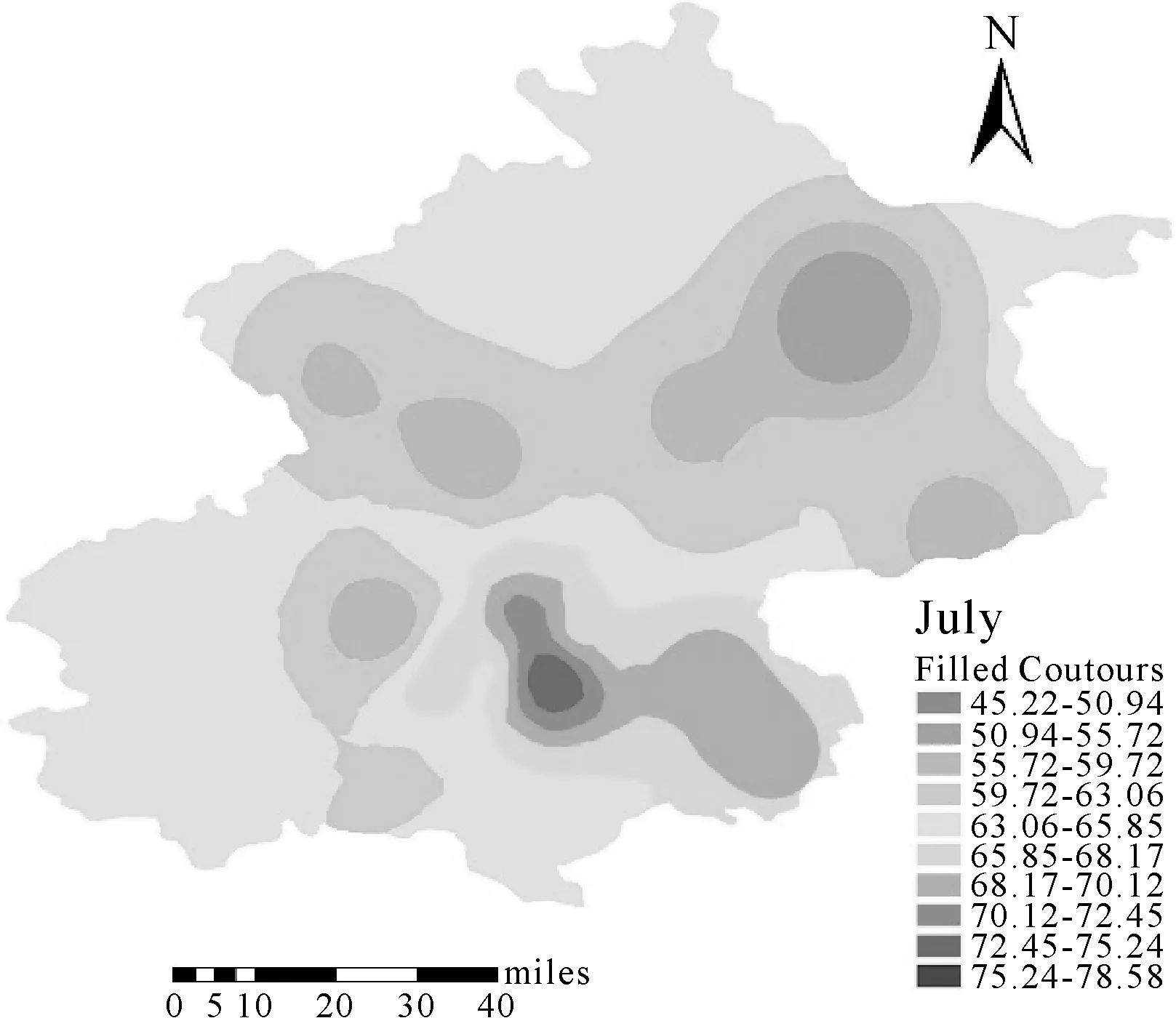
图8 7月PM2.5插值图

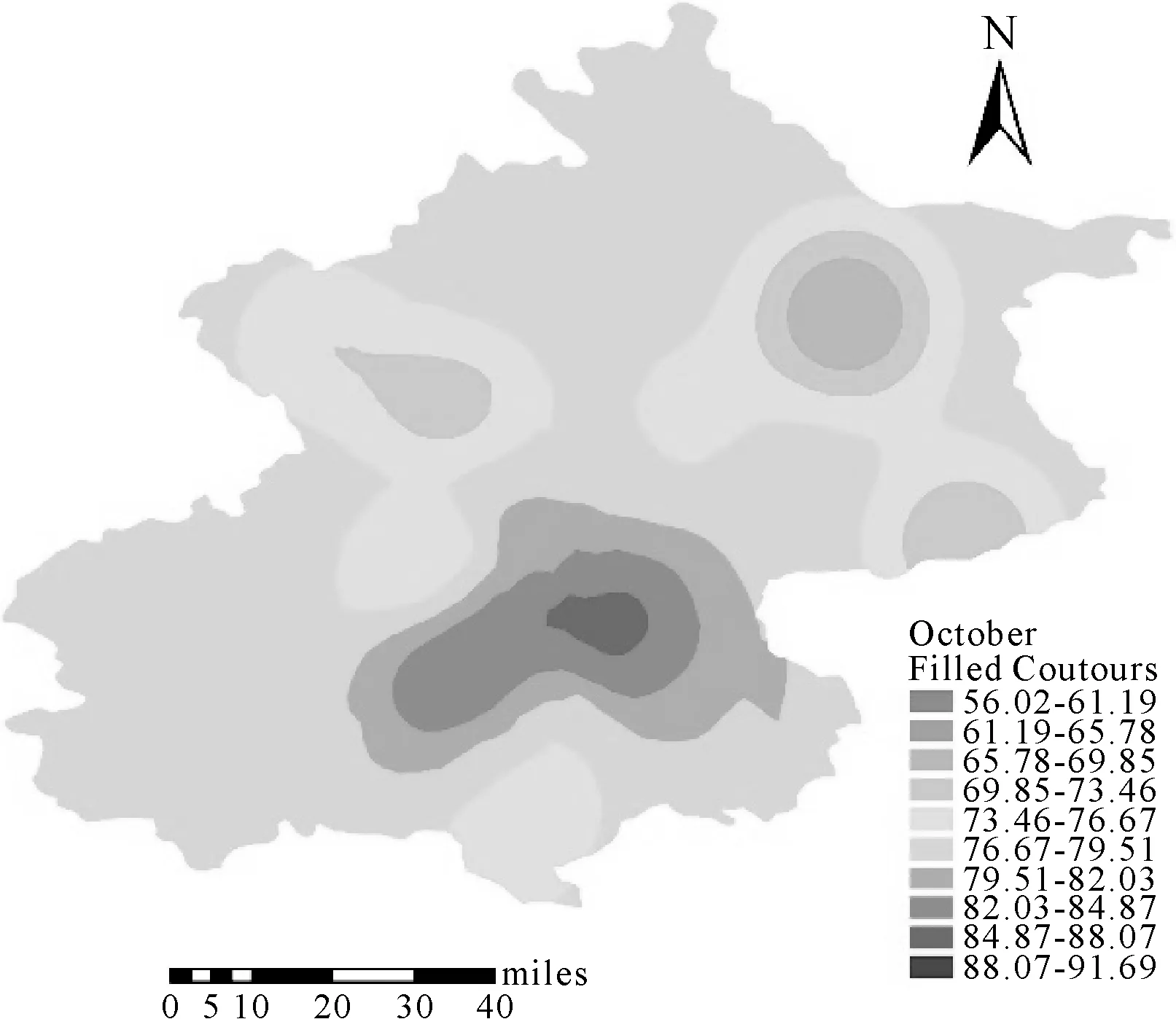
图9 10月PM2.5插值图

(3) 验证了文献[8]的结论：当主辅变量间的互相关性超过0.45的中等程度时，协同克里金法的插值精度明显优于普通克里金法。

(4) 通过本文方法解决了ArcGIS中协同克里金插值辅助变量最多考虑3个变量的限制。

本文由于数据限制只考虑了SO2、CO、NO2、O3和PM10浓度等因素，还有很多因素没有考虑(如风力、降水等)，但也说明该方法的优势，且在影响主变量的相关变量较多时更能体现出本文方法的优势，本文方法对今后研究空间插值具有一定的借鉴意义。

[1] 任阵海, 万本太, 苏福庆，等. 当前我国大气环境质量的几个特征[J].环境科学研究,2004,17(1):1-6.

[2] 赵越, 潘钧, 张红远，等. 北京地区大气中可吸入颗粒物的污染现状分析[J].环境科学研究,2004, 17(1):67-69.

[3] 陈义珍, 赵丹, 柴发合，等. 广州市与北京市大气能见度与颗粒物质量浓度的关系[J].中国环境科学, 2010，30(7): 967-971.

[4] 韩素芹, 张裕芬, 李英华，等. 天津市春季气溶胶消光特征和辐射效应的数值模拟[J].中国环境科学, 2011,31(1):8-12.

[5] TIE X, WU D, BRASSEUR G. Lung Cancer Mortality and Exposure to Atmospheric Aerosol Particles in Guangzhou,China[J]. Atmospheric Environment,2009,43(14):2375-2377.

[6] CAO J, XU H, XU Q, et al. Fine Particulate Matter Constituents and Cardiopulmonary Mortality in a Heavily Polluted Chinese City[J]. Environmental Health Perspectives,2012,120(3):373.

[7] 李正泉, 吴尧祥. 顾及方向遮蔽性的反距离权重插值法[J].测绘学报,2015,44(1):91-98.

[8] 石朋,芮孝芳.降雨空间插值方法的比较与改进[J].河海大学学报(自然科学版),2005,33(4):361-365.

[9] 李杰,翟亮,桑会勇,等. PM2.5浓度插值中不同空间插值方法对比[J].测绘科学,2016,41(4):50-54.

[10] 赵晨曦,王云琦, 王玉杰,等.北京地区冬春PM2.5和PM10污染水平时空分布及其与气象条件的关系[J].环境科学,2014,35(2):418-427.

[11] 梅杨，党丽娜,杨勇,等.基于时空克里格的PM2.5时空预测及分析[J].环境科学与技术,2016, 39(7):157-163.

[12] 程念亮,李云婷,张大伟,等.2013年北京市细颗粒物时空分布特征研究[J].环境工程,2015, 33(10):43-46.

[13] 彭彬,周艳莲,高苹,等.气温插值中不同空间插值方法的适用性分析——以江苏省为例[J].地球信息科学学报, 2011, 13(4):539-548.

[14] 王平,李浩,陈帅,等.基于坡度的黑土区切沟密度协同克里格插值方法研究[J].水土保持研究,2014, 21(6):312-317.

[15] 姜勇,李琪,张晓珂,等.利用辅助变量对污染土壤锌分布的克里格估值[J].应用生态学报,2006, 17(1):97-101.

[16] 范晓梅,刘高焕,刘红光.基于Kriging和Cokriging方法的黄河三角洲土壤盐渍化评价[J].资源科学, 2014, 36(2):321-327.

[17] 郭龙,张海涛,陈家赢,等.基于协同克里格插值和地理加权回归模型的土壤属性空间预测比较[J].土壤学报, 2012, 49(5):1037-1042.

[18] 赵彦锋,郭恒亮,孙志英,等.基于土壤学知识的主成分分析判断土壤重金属来源[J].地理科学,2008, 28(1):45-50.

[19] 梁丹.重庆市PM_(2.5)污染分布特征及影响因素分析[D].北京:北京林业大学,2016:19-23.

[20] 周一敏,赵昕奕.北京地区PM2.5浓度与气象要素的相关分析[J].北京大学学报(自然科学版), 2017(1):111-124.

[21] 王琪.基于北京市PM_(2.5)污染数据的特征提取及相关分析研究[D].北京:北京化工大学,2015:25-57.

[22] 章清,张海涛,郭龙,等.基于主成分分析的协同克里格插值模型对土壤铜含量的空间分布预测[J].华中农业大学学报, 2016(1):60-68.

[23] 张崇甫,陈述云.成分数据主成分分析及其应用[J].数理统计与管理, 1996(4):11-14.

[24] 王晓鹏,曾永年,丁生喜,等.基于改进主成分分析方法的复杂环境系统质量评价模型[J].系统工程理论与实践,2005,25(11):112-118.

[25] 叶双峰.关于主成分分析做综合评价的改进[J].数理统计与管理,2001,20(2):52-55.

[26] ASLI M, MARCOTTE D. Comparison of Approaches to Spatial Estimation in a Bivariate Context[J]. Mathematical Geosciences, 1995, 27(5):641-658.

[27] HASSANI S, MARTENS H, QANNARI E M, et al. Degrees of Freedom Estimation in Principal Component Analysis and Consensus Principal Component Analysis[J]. Chemometrics & Intelligent Laboratory Systems, 2012, 118(19):246-259.

[28] 姜晓剑,刘小军,黄芬,等.逐日气象要素空间插值方法的比较[J].应用生态学报,2010,21(3):624-630.

ACoKrigingInterpolationMethodBasedonPrincipalComponentAnalysis

LU Yueming1,WANG Liang1,QIU Agen1,ZHANG Yongchuan1,2,ZHAO Yangyang1

(1. Chinese Academy of Surveying and Mapping, Beijing 100830， China; 2. School of Resource and Environmental Science, Wuhan University, Wuhan 430079, China)

Aiming at the problem that the cooperative Kriging interpolation method has higher computational complexity when the auxiliary variables are numerous， and the interpolation precision is lower when the interpolation variables are less, a cooperative Kriging interpolation method based on principal components analysis is proposed (PCA-CoKriging). This method first uses the principal components analysis to reduce the dimension of the related interpolation variable, obtains several comprehensive indexes, and then uses these comprehensive indexes as the auxiliary variables to conduct cooperative Kriging interpolation. In order to verify the effectiveness of the method and the influence of the data distribution on the method, four groups of data about PM2.5concentration in the four seasons in Beijing in 2016 which meet different effects of normal distribution are selected, and PCA-CoKriging, ordinary Kriging interpolation method, and conventional Co-Kriging interpolation method are used to carry out interpolation experiments. The results show that the mean square error in the method of this article, ordinary Kriging interpolation method, and conventional Co-Kriging interpolation method are 4.91, 6.04 and 5.61 respectively, and the average root mean square errors are 6.65, 8.76 and 7.57 in the four groups. In comprehensive comparison, the mean absolute error and root mean square error in the proposed method have increased by 10.73% and 12.56% respectively compared with those of the conventional CoKriging interpolation, and 18.71% and 24.09% respectively compared with those of the ordinary Kriging interpolation method.

principal component analysis；CoKriging；Pearson correlation coefficient； PM2.5

卢月明，王亮，仇阿根,等.一种基于主成分分析的协同克里金插值方法[J].测绘通报，2017(11)：51-57.

10.13474/j.cnki.11-2246.2017.0347.

P208

A

0494-0911(2017)11-0051-07

2017-04-21

测绘新技术系统开发与示范应用(2016KJ0104)

卢月明(1991—)，男，硕士生，主要研究方向为空间数据挖掘和地理信息系统应用。E-mail：925651787@qq.com