郑徐高铁开封段地面沉降分层监测方法

张 丹，郝亚东

(1. 黄河水利职业技术学院测绘工程学院，河南 开封 475003； 2. 河南理工大学矿山空间信息技术国家测绘地理信息局重点实验室，河南 焦作 454003)

郑徐高铁开封段地面沉降分层监测方法

张 丹1,2，郝亚东1

(1. 黄河水利职业技术学院测绘工程学院，河南 开封 475003； 2. 河南理工大学矿山空间信息技术国家测绘地理信息局重点实验室，河南 焦作 454003)

高铁沿线施工期间引起地面沉降的因素错综复杂、相互影响，本文提出通过对沉降区域地下水位、孔隙水压力等进行分层观测，根据分层观测得到地下水位变化、孔隙水压力变化等数据，并采用回归分析法构建了沉降区域地面沉降与诸影响因子的关联模型，通过对郑徐客运专线开封段进行的地面沉降监测量与同时采用二等精密水准测量得到的监测点沉降量进行对比分析，结果表明本方法的有效性和可靠性。

高铁；地面沉降；分层监测；回归分析

郑徐客运专线是《国家中长期铁路网规划》“四纵四横”中的徐州至兰州铁路客运专线的重要组成部分。郑徐高铁客运专线西起郑州东站、东至徐州东站，线路全长361.937 km，其中开封段59.5 km。开封段地处黄淮冲积平原，沿线为较厚层第四系地层覆盖，地面表层的软土厚度较大。郑徐客运专线采用无砟轨道，轨道路基容许沉降值为15 mm，对路基进行沉降控制显得尤为重要。此外，由于开封段沿线地下水大规模开采所引起的地面沉降较为突出，对高铁施工及运营维护造成了严重影响。因此，研究郑徐客运专线开封段沿线地面沉降监测方法，为客运专线施工过程进行沉降控制，保证高铁安全运营具有重要意义。

1 地面沉降分层监测

1.1 分层监测原理

地面沉降分层监测是在土层不同深度及不同层位分别埋设沉降磁环，当沉降磁环受到土层不断压缩变形所产生的应力作用时其位置会发生变化，根据位移量就可以确定土层土体的压缩固结量，从而监测土体的垂直位移量(即沉降)。地面沉降分层监测系统由沉降磁环、沉降管、沉降观测仪等设备构成，当沉降观测仪内部的磁感应测量探头接触沉降磁环时，受磁场作用后其电流会发生变化。分层沉降观测仪内部有一个变化极小的钢尺(长度在50～100 m)连接在测量探头端部，与探头一起安置在分层沉降管中，用以监测分层沉降磁环的高度变化。

对地面进行分层沉降监测时，设每个分层沉降磁环的初始读数为D0i(分层沉降磁环到管口的距离)，每次观测沉降磁环的读数为Di，设分层沉降管口的初始高程为H0，则各分层沉降磁环的初始高程为H0-D0i，每次观测各个分层沉降磁环的高程为H0-Di，则各分层沉降磁环历次测量的沉降量hi可依据下式计算

hi=(H0-D0i)-(H0-Di)

(1)

根据每次分层沉降磁环的沉降量，可推算出各分层沉降磁环所处土层的压缩量为

H=hi-1-hii=2,3,…，n

(2)

将所有土层的压缩量进行叠加，可得到整个土层的压缩总量为

(3)

1.2 分层监测井标布设

郑徐高铁开封段地面沉降监测共布设包括D3水位分层监测孔及F3-1、F3-2分层沉降监测孔16个，地下水分层监测孔是在同一钻孔内安装多套井管，起到各自成井、分层止水及分层监测水位等作用。采用上述成井工艺，可节约征占土地费用、减少钻探进尺和进场次数，达到节约成本、提高效益，缩短工期和便于维护与管理等目的。

1.3 分层监测内容

1.3.1 孔隙水压力观测

对土体进行真空预压加固后，随着载荷增加，土体将出现不稳定现象。为掌握土体中有效应力的变化情况，需要监测孔隙水压力变化。土体受荷载后会产生孔隙水压力变化，并引起土体运动。监测不同深度土层的孔隙水压力变化、土压力变化，依据监测数据可以分析土体的有效应力及土体强度随时间变化的规律，据此计算沉降量或反演土层的固结系数，从而得到土层的固结度。

孔隙水压力观测需要首先埋设孔隙水压力计,然后观测孔隙水压力的初始值，该过程需要持续观测一周，取平均值观测值作为初始值。孔隙水压力计算公式如下

u=k(f2i-f20)

(4)

式中，μ为孔隙水压力(单位：kPa)；k为标定系数(kPa/Hz2)；fi、f0为测试频率、初始频率(Hz)。

1.3.2 地下水位观测

由于高铁路基施工过程中载荷在不断增加，从而会引起铁道沿线的地下水变化。因此，通过观测铁道沿线地下水位的变化状况，则可以掌握地面沉降情况。地下水位观测有以下两种方法：

(1) 观测孔设在施工区域外。通过外围观测，求出外围地下水位的变化。

(2) 观测孔设在施工区域内。通过观测该区域地下水位变化，为分析和计算地面沉降提供资料与依据。

2 沉降观测数据处理

地下水位、孔隙水压力及地面载荷等是引起高铁沿线地面沉降的主要因素，各种因素影响不尽相同，且相互影响，关系错综复杂。本文对多期观测数据采用回归分析法，旨在建立铁路沿线地面沉降量与诸因素之间的关联模型。

2.1 地下水位沉降模型

以地面作为参考基准面，当地下水位下降到深度H时，地表某点的沉降量δH可依据土力学中的沉降公式计算

δH=a0+a1H+a2H2

(5)

式中，H为该点抽水后的地下水位；a0、a1、a2可视为常数。

2.2 孔隙水压力沉降模型

孔隙水压力是各土层变形的重要监测量，其引起的地面沉降可表示为孔隙水压力p的函数，依据土力学中沉降公式，用泰勒级数展开后为

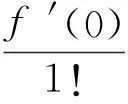
(6)

式(6)可表示为

δp=f(p)=b0+b1p+b2p2

(7)

2.3 时效因子模型

依据有效应力原理，土体变形与有效应力有关，某时刻t的沉降量δt为

δt=C1t+C2lnt

(8)

式中，C1、C2为有效应力系数。

2.4 基于回归分析的地面沉降模型

引入回归分析方法，综合考虑各种因素的变化影响，地面沉降计算模型为

δ总=a0+a1H+a2H2+b1p+b2p2+d1M+d2M2+c1t+c2lnt

(9)

式中，H、p、M为地下水位变化量、孔隙水压力变化量和地面荷载变化量；t为时效分量；ai、bi、ci、di(i=0,1,2)为系数。

3 实例验证

3.1 分层沉降观测方法

本文以开封段59.5 km区域为例进行沉降监测研究，具体方法是沿高铁线路无砟轨道的桩基上布设沉降监测点36个，采用二等精密水准测量进行往返观测。以无砟轨道桩基及轨道箱梁施工期间作为监测期，观测周期为1次/月，共进行20次。在进行水准测量的同时，利用16个分层监测井标观测地下水位计测出的各层地下水位变化量、孔隙水压力变化量，并在无砟轨道施工期间开展地面荷载变化分析。水准测量与分层监测井标观测同时进行，分别计算沉降结果，并对沉降结果进行对比分析，从而判断分层监测结果的可靠性和分层监测方法的可行性。

3.2 结果分析

采用二等精密水准测量观测得到的部分监测点累计沉降结果见表1；根据分层监测井标观测的地下水位变化、孔隙水压力变化，基于回归分析法建立的地面沉降模型计算的监测点沉降结果见表2。

表1 监测点累计沉降结果

表2 回归分析数学模型计算沉降结果

对比表1和表2两种监测方法结果可以看出，其最大偏差δmax=±0.3 mm、最小偏差δmin=±0.1 mm，两种方法计算结果较为吻合，表明根据分层监测井标观测的地下水位变化量和孔隙水压力变化量，与采用回归分析地面沉降数学模型计算监测点地面沉降方法，均适合于郑徐高铁(开封段)地面沉降监测。

4 结 语

针对高铁线路施工过程中采用常规方法监测地面沉降，存在工作量大、监测周期频率高、施工交叉作业相互影响等不足，本文采用分层监测方法对郑徐高铁开封段进行沉降监测研究，通过观测地下水位、孔隙水压力、基于回归分析模型计算地面沉降量，结果表明该方法适用于厚层软土的地面沉降监测，同时本文采用的一孔多井、分层观测方法，可有效减少钻探进尺与进场次数，提高作业效益，便于维护与管理。

[1] 凌柏平，龚永康，张建跃.真空预压软基处理分层沉降监测[J].水运工程，2010(12):129-134.

[2] 苏国祥，王简年. 真空预压软基处理工程监测[J].港工技术,2009(7):116-119.

[3] 颜波，周诗庆，张红芹. 真空预压软基处理孔隙水压力与地下水位监测研究[J].江西科学,2010(8):473-475.

[4] 郝亚东，许加东，张勇. 基于多影响因子计算模型在城市地面沉降监测应用研究[J].铁道工程学报，2011，28(3):20-23.

[5] 曹凯，黄腾志.温州丁山垦区真空预压软基处理监测方案[J].基础与结构工程,2012(6):131-135.

[6] 詹学启，张占荣. 郑徐高速铁路郑州段区域地面沉降预测分析[J].铁道标准设计, 2014(7):56-60.

[7] 唐华桥. 真空预压软基处理分层沉降监测探析[J].科技传播, 2014(2):193-194.

[8] 卢小平，朱宁宁，卢遥，等. 基于激光点云的隧道断面连续提取与形变分析方法[J]．测绘学报，2015,44(9):1056-1062.

[9] 高昂，张孟喜，蒋华钦，等. 地面出入式盾构法隧道施工同步注浆工程应用研究[J].岩石力学与工程学报,2016，35(9):1871-1883.

[10] 吕伟华，邵光辉. 基于单井抽水模型试验的含水层变形特性[J].林业工程学报,2016，1(3):115-120.

[11] 吴意谦，朱彦鹏. 考虑侧向变形下抽降潜水引起地面沉降的计算[J].华中科技大学学报(自然科学版),2016，44(4):116-120.

[12] 姜媛，田芳，罗勇，等. 北京地区基于不同地面沉降阈值的地下水位控制分析[J].中国地质灾害与防治学报,2015，26(1):37-42.

[13] 叶俊能，郑铣鑫，侯艳声. 宁波轨道交通规划区域地面沉降特征分析及监测[J].水文地质工程地质,2010(3):107-111.

[14] 王建秀，吴林高，朱雁飞，等. 地铁车站深基坑降水诱发沉降机制及计算方法[J].岩石力学与工程学报,2009，28(5):1010-1019.

[15] 刘寒鹏，杜东菊，孙锐. 真空预压软基处理沉降监测分析[J].工程地质学报,2009，17(1):111-114.

[16] 唐益群，栾长青，王建秀，等. 上海某地铁站试降水对周边环境的影响分析[J].武汉理工大学学报,2008，30(8):147-151.

[17] 龚士良. 台湾地面沉降现状与防治对策[J].中国地质灾害与防治学报,2003，14(3):24-31.

[18] 刘欢欢，张有全，王荣，等. 京津高铁北京段地面沉降监测及结果分析[J]. 地球物理学报,2016，59(7):2424-2432.

[19] 卢小平，朱宁宁，禄丰年. 基于椭圆柱面模型的隧道点云滤波方法[J].武汉大学学报(信息科学版)，2016,41(11):1476-1482.

TheLandSubsidenceStratificationMonitoringofZheng-XuHigh-speedRailwayinKaifengSection

ZHANG Dan1,2,HAO Yadong1

(1. Yellow River Conservancy Vocational and Technical College, Kaifeng 475003, China; 2. Key Laboratory of Mine Spatial Information Technologies, NASG, Jiaozuo 454003, China)

In this paper, the factors that cause the land subsidence during the construction of high-speed railway are complicated and interactional. It is proposed that the ground water level and pore water pressure in the subsidence area are stratified observation, and the data of groundwater level change and pore water pressure change are obtained according to stratified observation. Regression analysis method to construct the correlation model of land subsidence and its influence factors in settlement area.The land subsidence monitoring of Zheng-Xu high-speed Kaifeng section is compared and analysed with the same period using second class precision level measurement points settlement. The results show that the method is effective and reliable.

high-speed rail; land subsidence; stratification monitoring; regression analysis

张丹，郝亚东.郑徐高铁开封段地面沉降分层监测方法[J].测绘通报，2017(11)：77-79.

10.13474/j.cnki.11-2246.2017.0352.

P258

A

0494-0911(2017)11-0077-03

2017-07-15；

2017-08-28

2016年度国家重点研发计划重点专项(2016YFC0803103)

张 丹(1980—)，男，硕士，讲师，主要从事测绘科学与技术教学及研究工作。E-mail：40663113@qq.com