空间用贮箱流固耦合动力特性分析

姚 灿，朱洪来，林星荣

（1.北京控制工程研究所，北京 100094；2.北京市高效能及绿色宇航推进工程技术研究中心，北京 100094）

空间用贮箱流固耦合动力特性分析

姚 灿1，2，朱洪来1，2，林星荣1，2

（1.北京控制工程研究所，北京 100094；2.北京市高效能及绿色宇航推进工程技术研究中心，北京 100094）

针对薄壁贮箱的流固耦合问题，在理论分析基础上，采用有限元数值方法进行贮箱在充液不加压和充液加压两种工况下的模态分析，得到流固耦合下贮箱的含阻尼非线性固有频率等动力学参数。最终，总结和分析流固耦合动力学分析结果，给出了贮箱在设计和使用过程中需要关注的两点：一是振型基本均为呼吸状，二是流体的密度、声速会影响流固耦合模型的模态频率。

贮箱；流固耦合；动力学；固有频率

1 引言

贮箱是空间飞行器的一个重要组成部分，就其结构方面来讲，基本特点是结构重量轻、刚度和强度要求高。贮箱本身填充大量液体，同时保持较高的压力，此外还需要经历较复杂的力学环境。因此薄壁压力容器的流固耦合问题，特别是动力学问题，一直是空间飞行器的关键问题之一［1-3］。

近几十年来，国内外学者对流固动力耦合的理论和计算方法开展了广泛研究，取得了一些成果［4］。但是，由于流固耦合问题的复杂性，无论在理论分析还是数值计算方面，还存在许多假设，远远没有达到理论与实践的统一。对于流固动力耦合系统的求解，比较简单的问题，可以采用解析法和半解析法，而具有复杂边界条件的实际工程问题，多采用数值方法研究［5］。

本文在理论分析基础上，采用数值方法进行贮箱在充液不加压和充液加压两种工况下的模态分析，得到流固耦合下压力容器的固有频率和振型等动力学基本参数。最后总结和分析数值仿真结果，给出设计和使用等过程中需要关注的因素。

2 数值模型与数值方法

2.1 控制方程

2.1.1 结构动力学方程

对于线性结构，瞬态动力学基本方程如式（1）：

其中，M为结构质量矩阵，C为结构阻尼矩阵，K为结构刚度矩阵，u¨为节点加速度向量，u·为节点速度向量，u为节点位移向量，f为外部载荷向量。

2.1.2 流体力学基本方程

对于不可压缩粘性流体，在直角欧拉坐标系下，其运动规律受N-S方程控制，连续性方程和动量方程分别如式（2）、式（3）所示：

其中，ρ为任意空间点密度，vi为任意空间点速度，P为任意空间点压力，v为运动黏度。

2.1.3 流固耦合基本方程

为精确描述流体与结构的相互作用，将流体压力作为载荷施加到流体与结构交界面上。综合固体与流体控制方程，流固耦合问题有限元控制方程可以整理为式（4）：

其中，

p表示来自流体的变量，fs表示流体结构的相互作用，e表示来自结构的变量。

2.2 数值模型与边界条件

分别建立固体域和流体域模型。在对模型进行切分和布尔运算过程中，保证流体划分的网格可以与固体进行共节点处理，从而保证流固耦合模态计算结果的准确性。处理后的模型见图1壳体流体组合图和图2流体域模型。

壳体模型采用四边形进行网格剖分，流体域模型采用六面体网格进行剖分。此外还需定义流固耦合交界面，见图3。施加法向约束，下圆柱段施加固定端约束。

3 计算结果

本次计算中选取了空间任务中常用的两种推进剂作为填充的液体，分别是液体1：MMH、液体2：N2O4，其物性参数如表1所示。

表1 填充液体参数Table 1 Parameters of the filling liquid

3.1 充液不加压模态分析

贮箱里面充液95%，由于存在流体结构相互作用，质量、刚度等不再是对称矩阵，所以采用非对称求解算法Unsymmetric法进行模态分析。为对比分析，分别计算贮箱充液体1与不充液两种工况，并计算贮箱前10阶流固耦合含阻尼非线性模态。

贮箱充液体1的1阶振型为呼吸状，如图4所示。表2给出贮箱充液体1与不充液两种工况频率对比结果。

表2 模态频率对比结果Table 2 Results of modal and frequency comparison

3.2 充液预应力模态分析

贮箱充液95%后，上部5%的内壁承受1.75 MPa的内压、贮箱的自重以及液体自重，使用Unsymmetric Method法进行模态分析。为对比分析，分别计算贮箱充液体1与充液体2两种工况，计算贮箱前10阶预应力流固耦合模态。

贮箱充液体1并加压工况下的1阶振型为呼吸状，如图5所示。表3给出贮箱充液体1与充液体2两种工况频率对比结果。

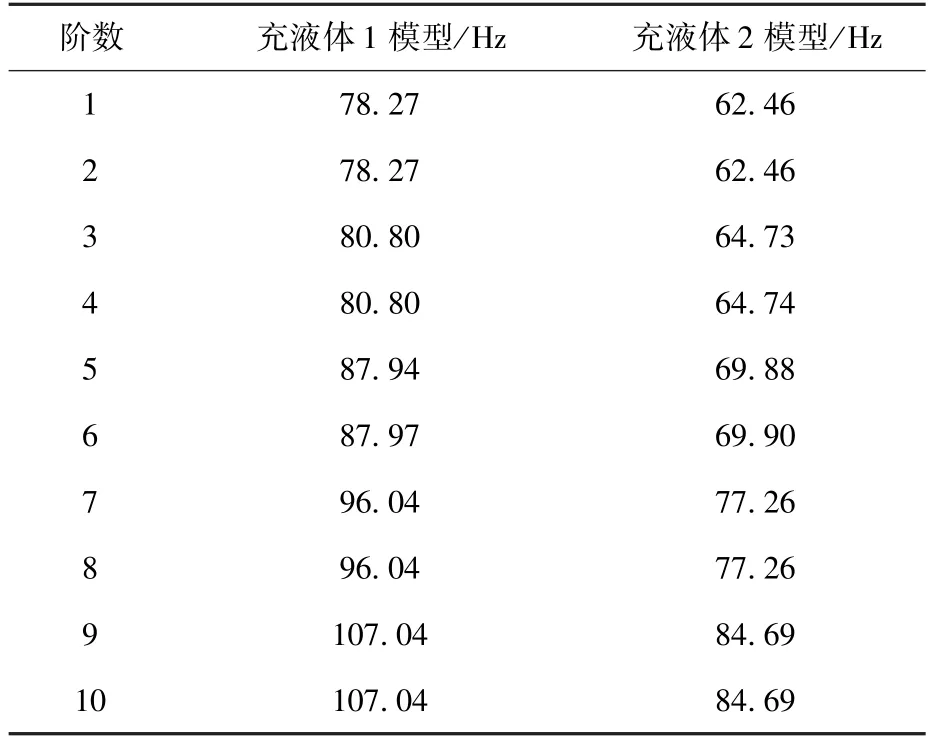
表3 模态频率对比结果Table 3 Results of modal and frequency comparison

4 结果分析

4.1 贮箱流固耦合模态分析

通过对不加液贮箱和充液体1不加压贮箱模态分析可得其频率对比如图6所示，对于相同阶数空贮箱的模态频率远大于贮箱内充液体但不加压的频率。随着阶数增加，空贮箱和充液体1不加压贮箱频率都是逐渐增高，但由于液体的阻尼作用，充液不加压贮箱频率增幅较小。

4.2 预应力贮箱流固耦合模态分析

对比图4和图5可知，填充同样的液体，加压与否对频率和振型均影响不大。通过对加压充液体1贮箱和充液体2贮箱的模态分析得到其频率对比如图7所示，从图中可知填充不同的液体，由于密度和声速的不同，贮箱的频率还是有明显变化，也就是流体的密度和声速对流固耦合模态频率影响较大。

5 结论

本文采用有限元数值方法进行贮箱在充液不加压和充液加压两种工况下的模态分析，得到结果如下：随着阶数增加，贮箱频率逐渐增高，但由于流体的阻尼作用，充液贮箱频率增幅较小；填充不同的液体，由于密度和声速的不同，贮箱的频率有明显的变化，也就是流体的密度和声速对流固耦合模态频率影响较大。

总结分析流固耦合动力学分析结果可知，在贮箱的设计和使用中，以下两点需要重点关注：

1）空壳与填充液体贮箱的振型基本均为呼吸状，但是其频率相差较大，实际应用过程中贮箱是填充液体的，因此在设计过程中要确认频率与运载飞行器不发生共振；

2）流体的密度、声速会影响流固耦合模型的模态频率，对于相同贮箱填充不同液体，其动力学特征不同，在应用过程中需要注意。

（References）

［1］ 朱琳，唐国安，柳征勇，等.推进剂与贮箱液固耦合振动的动力学分析［J］.振动与冲击，2012，31（5）：139-143.Zhu L，Tang G A，Liu Z Y，et al.Dynamic analysis for fluidstructure coupled vibration of propellants and fuel tank［J］.Journal of Vibration and Shock，2012，31（5）：139-143.（in Chinese）

［2］ 尹立中，王本利，邹经湘，等.圆柱贮箱类液固耦合系统转动响应分析［J］.振动工程学报，2001，31（5）：68-71.Yin L Z，Wang B L，Zou J X，et al.Analysis on dynamic response of the liquid-solid coupling systemwith the liquid in a cylindrical container under pitching excitation［J］.Journal of Vibration Engineering，2001，31（5）：68-71.（in Chinese）

［3］ 尹立中，赵阳，王本利，等.贮箱类液固耦合动力学研究［J］.工程力学，2000，17（5）：128-130.Yin L Z，Zhao Y，Wang B L，et al.On the dynamics of liquid／structure coupling of containers［J］.Engineering Mechanics，2000，17（5）：128-130.（in Chinese）

［4］ 朱洪来，白象忠.流固耦合问题的描述方法及分类简化准则［J］.工程力学，2007，24（10）：92-99.Zhu HL，Bai X Z.Description method and simplified classification rule for fluid-solid interaction problems［J］.Engineering Mechanics，2007，24（10）：92-99.（in Chinese）

［5］ 郝亚娟，白象忠，杨阳.贮箱中弹性隔层板在流体作用下的振动分析［J］.振动与冲击，2010，29（7）：132-134.Hao Y J，Bai X Z，Yang Y.Vibration analysis of elastic plate in a tank with fluid influence［J］.Journal of Vibration and Shock，2010，29（7）：132-134.（in Chinese）

Fluid-Structure Coupling Dynamic Characteristic Analysis for Tank of Aerospace

YAO Can1，2，ZHU Honglai1，2，LIN Xingrong1，2
（1.Beijing Institute of Control Engineering，Beijing 100094，China；2.Beijing Engineering Research Center of Efficient and Green Aerospace Propulsion Technology，Beijing 100094，China）

To solve the fluid-structure coupling problem of the thin wall tanks，a finite element numerical approach was adopted on the basis of theoretical analysis.Modal analysis was conducted for the non-pressurized and pressurized tanks with filling liquids and the dynamic parameters of the nonlinear normal natural frequency with damping were obtained.Then，the fluid-structure coupling dynamic simulation results were summed up and analyzed.The factors worthy of paying attention to in the process of designing and using the tanks were given such as the vibration modes of the tank were basically the breathing style，and the density and sound speed of the fluid would affect the modal frequency of the fluid-structure coupling model.

tank；fluid-structure coupling；dynamics；natural frequency

TQ051.7

A

1674-5825（2017）06-0751-04

2016-08-24；

2017-09-29

姚灿，男，硕士，高级工程师，研究方向为航天器推进技术。E-mail：yaocanbit＠163.com

（责任编辑：庞迎春）