基于元胞蝙蝠算法的无线传感器网络节点定位研究

孟凯露，岳克强，尚俊娜

（1. 杭州电子科技大学通信工程学院，浙江 杭州310018；2. 杭州电子科技大学电子信息学院，浙江 杭州 310018）

基于元胞蝙蝠算法的无线传感器网络节点定位研究

孟凯露1，岳克强2，尚俊娜1

（1. 杭州电子科技大学通信工程学院，浙江 杭州310018；2. 杭州电子科技大学电子信息学院，浙江 杭州 310018）

为了提高节点定位精度，解决定位误差较大的问题，提出了基于元胞蝙蝠算法的无线传感器网络节点定位算法，以此来获得更高的定位精度。首先将元胞自动机的思想融入蝙蝠算法，采用了改进的元胞限制竞争选择小生境技术和灾变机制，使得该算法在寻优过程中能够跳出局部极值，避免早熟现象，更快地收敛到全局最优解。通过标准测试函数的验证，表明了该改进算法在收敛深度和广度上的优势。之后将元胞蝙蝠算法应用到无线传感器网络节点定位上来提高定位精度。实测实验中，该算法在测试环境下平均定位误差在0.4 m以内，相比于改进PSO算法，获得更好的定位效果。

无线传感器网络；节点定位；元胞自动机；蝙蝠算法；定位精度

1 引言

无线传感器网络[1]由能够进行通信和计算的无线传感器节点组成，由于其成本低、功能多、融合多门技术，被誉为21世纪最具有影响力的技术之一。根据是否需要测量距离，目前无线传感器节点定位算法可以分为两种定位机制：基于测距和无需测距。基于测距的定位主要是通过距离来确定节点的位置，无需测距则不需要知道节点的距离和方向，只能通过估计定位节点的位置，而基于测距的定位精度远远高于无需测距的方法，将会有更好的发展空间。测距的基本方法包括接收信号强度指示（received signal strength indication，RSSI）、到达时间差（time difference of arrival，TDOA）、到达角度（angel of arrival，AOA）。RSSI[2]因其使用方便和精度高而被广泛应用。无线传感器的节点定位问题可以转换成一个多约束优化问题，当前有学者采用智能算法来提高节点定位的精度[3]，但常用的粒子群算法、遗传算法等智能优化算法易陷入局部最优，定位精度、效果的提高不明显，因此需要研究一种性能好、效率高的智能算法，从而有效地提高定位精度。

蝙蝠算法（bat algorithm，BA）模拟自然界中蝙蝠利用一种声纳来寻找猎物和避免障碍物的生物学特性，具有并行性、分布式和收敛速度快等特点[4]。目前，已经广泛应用于工程设计、分类、模糊聚类、预测和神经网络等领域。但是基础BA算法的搜索区域单一，缺乏有效方法保持种群的多样性，搜索性能较差。基于此，参考文献[5]将改进的蝙蝠算法应用于Dv-Hop定位算法平均跳距的计算过程中，使得该算法在不同锚节点密度、不同通信半径、不同节点数量以及定位精确度等方面的性能明显增强。参考文献[6]采用蝙蝠算法的拓扑结构来构建多智能体的体系结构，通过多智能体蝙蝠算法来求解室内定位，大大提高了算法的收敛速度和效率。多智能体之间虽然可以发生决策交互，也可以与环境相互作用，但是在深度搜索和保持个体多样性方面仍有待提高。

元胞自动机（cellular automata）是时间、空间上均表现为离散的动力系统模型，多个元胞在同一个环境里共同生存，且每个元胞能够主动地、自治地活动，基于此本文提出一种元胞蝙蝠算法（cellular automata bat algorithm，CA-BA），将CA的思想融入BA算法[7,8]中，把每个蝙蝠个体看作一个元胞，同时采用了改进的元胞限制竞争选择（restricted competition selection，RCS）小生境技术，将元胞与其邻域看作一个小生境环境，通过小生境环境内的最优解进行速度和位置的更新，并加入了灾变机制，使元胞个体能够较快地跳出局部极值从而避免早熟现象，提高了算法的效率。通过对6个标准测试函数的仿真，改进的CA-BA算法在寻优精度和收敛速度上都比BA算法、CBA算法以及 MA-BA算法更胜一筹，同时将其应用于无线传感器网络节点定位中，节点的平均定位误差相对较小，并且可以使用相对较少的锚节点达到理想的定位精度。

2 CA-BA算法

2.1 基本BA算法

由Yang教授于2010年提出的蝙蝠算法[9]是一种启发式的群体智能算法，基于蝙蝠的回声定位能力指导它们的捕食行为。在实际的优化算法中，每只蝙蝠为搜索解空间的一个点，由适应度函数来决定蝙蝠位置的优劣。蝙蝠个体的每一次有效飞行就是 BA算法的一次迭代更新。蝙蝠的位置和速度更新如下：

选取个体按式（2）进行最优解扰动：其中，ε为[−1,1]上的随机数值，tA为在时刻t所有蝙蝠个体的平均响度。当发现猎物的时候，蝙蝠个体则降低脉冲响度和增加脉冲频度。在BA 算法中，响度Ai和脉冲频度ri按式（3）进行更新：

其中，0ir表示初始脉冲频度，γ是发射脉冲

频度增加的系数，ω是脉冲响度衰减系数，两者都为常数，其中，0＜ω＜1，γ＞0。

2.2 CA-BA算法

元胞自动机[10]是一种时间和空间都离散的动力系统，散布在规格网格中的每一元胞取有限的离散状态，依据确定的局部规则作同步更新。本文将CA的思想应用到BA算法中，把BA算法中的个体看作元胞自动机系统（cellular automata system，CAS）中的元胞，以此来研究种群的交流结构以及信息传递与继承机制。根据元胞自动机的原理和规则，蝙蝠个体只与通过邻居函数确定的邻域个体进行交流[11]，并且能够由自身的局部搜索逐步延伸到全局搜索，这样使得寻优过程能够摆脱局部极值从而避免早熟，有助于保持种群的多样性和探索能力，更准确迅速地收敛到全局最优解。

2.2.1 元胞自动机与蝙蝠算法的混合机制

在所提出的CA-BA算法中，把BA算法中的一个蝙蝠个体看作一个元胞，且这个元胞只能与通过邻居函数确定的邻域元胞进行交流、竞争与合作，根据邻域环境更新自身的位置和速度。本文选取的是结构简单稳定的四方网格排列，如图1所示。每一个网格就表示CA-BA算法中的一个元胞，即一个蝙蝠个体。元胞在网格中的位置固定不变，每一个网格包含的信息是元胞的固定位置以及其在解空间的位置和速度。并且元胞的边界条件是周期型（pehodic boundary）的，即对于二维空间而言，上下相连，左右相连，元胞蝙蝠个体以相邻的8个元胞为邻居，即Moore邻居形式，假设图1中相邻两个方格的距离为1，它的邻域元胞可以由式（4）被定义：

j表示中心元胞的行列坐标值。此种CA-BA算法中蝙蝠元胞的重叠方式提供了一种隐性的迁移机制，有利于最优个体在种群中缓慢地扩散，能更持久地保持种群多样性。

图1 四方网格

2.2.2 改进的元胞RCS小生境技术

在基础BA算法中，算法前期收敛速度很快,但随着迭代次数的增加，蝙蝠种群聚集现象比较严重，蝙蝠个体的速度逐渐减小并趋于0，这导致算法后期易陷入局部极值而停滞不前，因此如何保持种群个体的多样性对蝙蝠算法进行深度搜索具有十分重要的意义。基于上述分析本文引入小生境策略来维持种群的多样性。

将元胞Xi,j与其邻域个体其中，num为1～8的整数，看作一个小生境环境，记录其邻域最优元胞为

,

i j M ，首先比较Xi,j与Mi,j的适应度值。按照以下步骤对元胞个体进行进化：

明距离，并将距离值按照从大到小排序。

其中， L' e vy( 0,1)为L' evy分布函数，通过扰动不仅加快了算法向最优解区域靠近的速度,而且提高了算法跳出局部极值的能力和寻优精度，提高了算法的寻优性能。

通过RCS小生境技术，保证了元胞个体向最优个体的学习，元胞与邻域元胞互相传递有效信息，并且通过不同邻域中重叠的元胞将有效信息传递到整个空间网格中，从而与全局最优元胞进行信息的交流。并且在信息交流的过程中，元胞的行动策略得以修正，从而增强了局部搜索能力和加快了算法收敛到最优解。同时通过L' evy扰动，元胞邻居个体位置的随机更新，提高了种群的多样性，避免了算法陷入局部最优的情况。

2.2.3 元胞蝙蝠个体灾变机制

为避免CA-BA算法出现早熟现象，本文采用了一种简单有效的方法，在模拟自然界的状况下进行灾变操作[12,13]。基本思想为：以某一确定的频率对固定面积的元胞进行扰动。在该扰动半径内的个体会发生变化，使其跳出局部最优解，开始进行新的搜索。具体操作是：选取即每隔10代对群体进行一次扰动，选取扰动面积为1×1，即扰动半径为1。将灾难发生区域的个体进行清零操作，并随机植入优良个体。引入的灾变机制，可以使CA-BA算法跳出局部极值，保持持续进化能力。

2.3 CA-BA算法步骤

步骤 1初始化种群。按照图 1的形式构造元胞的四方网格排列方式，即给定种群的生存环境和规模，在限制范围内随机初始化元胞的速度v、位置x和发射脉冲频率 f，并给定初始脉冲频度r0和脉冲响度A0。

步骤2计算所有元胞的适应度值 Fitness( i)。用计算出的适应度值更新元胞的极值，并比较各个元胞的极值，求出种群的全局最优解和其对应的适应度值

步骤3构造小生境环境，调整元胞的位置。利用式（4）计算出元胞Xi,j的8个邻居，并将其看作一个小生境环境，找出邻域的最优元胞为Mi,j。若Xi,j的适应度值优于Mi,j，则保留Xi,j在解空间中的位置，并记为neigh(x*)，且按式（6）改变与Xi,j距离最近的元胞Ci,j的位置；若Mi,j的适应度值优于Xi,j，则记Mi,j的位置为 neigh( x*)，并按式（6）和式（7）改变Ci, j和Xi,j在解空间中的位置。

步骤4通过式（1）的3个计算式完成所有元胞的一次迭代过程，即更新每个元胞在解空间中的位置x和速度v，注意式（2）中的全局最优值 x*要用邻域最优解 neigh( x*)替代，并记录更新后元胞的适应度值为Fnew。

步骤 5生成均匀分布随机数rand1，若rand1 ＞r( i)，则根据式（2）对当前最优解进行随机扰动，并对新解进行越界处理和计算其适应度值。如果不满足条件则跳过该步。

步骤6生成均匀分布随机数rand2，若满足条件 Fn ew ＜Fitness( i) & rand 2 ＜ A( i )，则接受步骤5产生的新解，并根据式（3）更新脉冲响度A和发射脉冲的频度r。如果不满足条件表示该元胞的位置更新失败，跳过该步。

步骤 7比较新解和原来全局最优解的适应度值，若满足 F new ＜f( x*)，则进行全局最优解Cell( x*)和其对应的适应度值 f( x*)的更新。否则跳过该步。

步骤 8若 generation =rem( g eneration)=10（即每隔 10代发生一次灾变），将灾难区域个体清空，并植入优良个体。

重复步骤2～步骤7，直至满足最优解要求的精度或达到最大迭代次数，当满足要求后输出全局最优解以及其对应的最小适应度值。

2.4 CA-BA算法性能测试

智能算法的性能一般由标准测试函数进行验证，因此本文选取了 6个标准测试函数对 CA-BA算法的性能进行仿真测试，同时与基本BA算法、具有混沌搜索策略的蝙蝠算法（chaos bat algorithm，CBA）[4]以及参考文献[6]所改进的多智能体蝙蝠算法（multi-agent bat algorithm，MA-BA）进行对比。2.4.1 参数设置

蝙蝠算法中各种参数设置目前没有明确的理论依据，因此本文所设置的参数值根据反复实验获得的经验值来确定。CA-BA算法中：元胞总数N=64，四方网格的大小为 8×8，维数 d=5，搜索脉冲频率范围[0,100]，最大脉冲频度 r=0.5 ，最大脉冲音强A=0.25，脉冲音强衰减系数γ=0.95，脉冲频度增加系数α=0.05。BA算法、CBA算法、MA-BA算法中的各个参数与CA-BA算法保持一致。这3个算法的最大迭代次数都是200次，每种算法独立运行50次。其中，CBA表示具有混沌搜索策略的蝙蝠算法，MA-BA 表示多智能体蝙蝠算法，CA-BA表示元胞蝙蝠算法。

2.4.2 标准测试函数

仿真分析选取的测试函数的解析式和解空间搜索区域见表1。对于仿真所用的标准函数可以分为 2类：Quadric、Rosenbrock、Schwefel是单模函数，是测试算法全局收敛性能的经典函数；Ackley、Griewank、Rastrigin是具有较多局部极值的多模函数，主要用来评价算法的探索、开发能力。

2.4.3 仿真效果分析

图2显示了以上6个标准函数在BA、CBA、MA-BA以及CA-BA算法中的寻优曲线。CA-BA算法采用了改进的元胞RCS小生境技术，将元胞和其邻域个体看作一个小生境环境，通过小生境环境中的最优解来更新自身的速度与位置，具有较强的适应性和搜索能力，并且采用了灾变机制，避免了元胞因陷入局部最优解而难以跳出的情况，该算法能够更高效地收敛到全局最优解。从图2的仿真结果可以看出，相比其他3个算法来说，CA-BA算法在寻优精度和收敛速度上更胜一筹，在较少的迭代次数内达到所要求的最优解。这些都体现出了将CA的思想融入BA算法之后，大大加强了算法的搜索能力，使其能够避免早熟，更快地收敛到全局最优解。

表1 标准测试函数

图2 标准测试函数寻优曲线

在仿真参数如上文中所设置的情况下，将上述标准函数测试的寻优结果取100次进行平均，见表2，同时用成功率来表示算法的稳定性，对于单模函数，是以其理论最优值的1‰为标准，多模函数以最优理论值的5‰为标准，如果最小适应度值小于以上标准则是取得了正确解。从表 2可以看出，CA-BA算法的寻优成功率相比 BA算法、CBA算法和MA-BA算法来说较高，平均最小适应度值较接近于理论最优值。

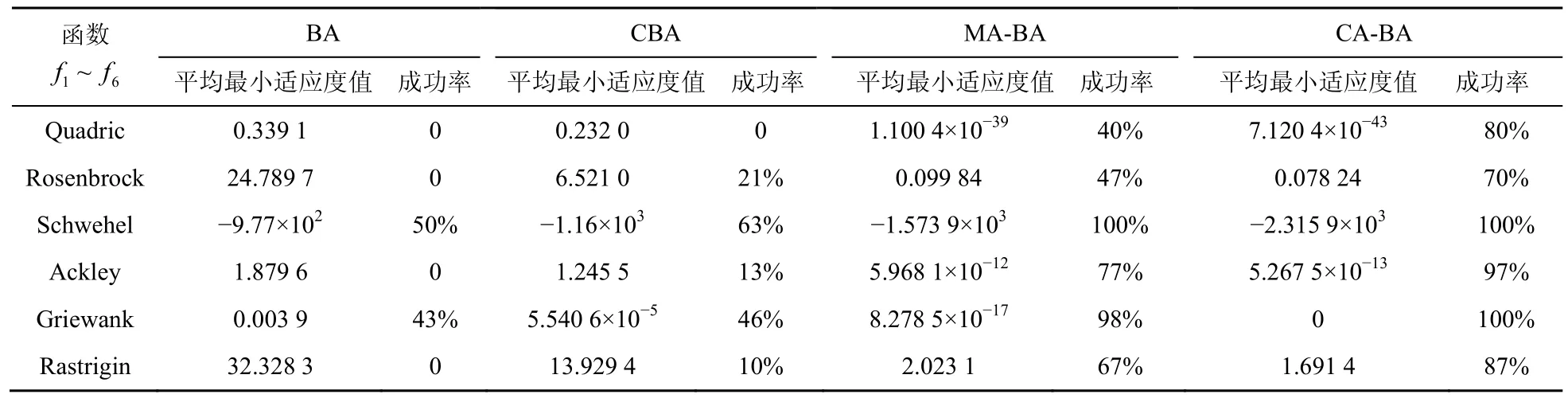
表2 标准函数测试结果

3 CA-BA 算法在无线传感网络节点定位中的应用

通过上述分析，验证了CA-BA算法在测试函数中的性能，接下来将CA-BA算法应用在无线传感器网络节点定位问题上，通过该算法在最优解寻优精度上的结果来验证其性能[14]。对于无线传感器节点网络中共有 M个已知节点，其中，(x1,y1), (x2,y2), …, (xM,yM)为 M个已知节点的坐标，(x, y)为任一未知节点的坐标，d1,d2,…,dM分别为各个锚节点到该未知节点坐标的距离。在实际的测距中存在误差，因此可以将定位问题转化为式（8）求测距误差最小值的优化问题：

由上述仿真分析可知，CA-BA算法能够避免元胞陷入局部最优值以及具有较好的收敛性能，因此将该算法应用到实际测距中，即求式（8）的最小值，能够减小实际测距误差带来的影响，从而提高未知节点的定位精度。

3.1 仿真分析

仿真实验以MATLAB 2012为平台，节点的通信半径设置为 10 m，30个传感器随机分布在30 m×30 m的四方网格区域内，测距误差在20%以下，锚节点个数为5，仿真参数与上文设置相同，最大迭代次数为200次，每一个节点定位预测取20次平均值。将CA-BA算法与参考文献[6]中的MA-BA算法进行节点定位结果的对比，见表3。本算法在RSSI的基础上对定位精度进行优化。在仿真中，以平均定位误差的绝对值AVE作为评判的标准，其计算式如式（9）所示：

其中，M为已知节点的总个数，(x, y)为预测位置，(xi, yi)为实际位置。

表3选取了10个未知节点预测的具体数值作比较，由表3可知，本文所提出的基于CA-BA算法的节点定位精度比参考文献[6]中的节点定位精度平均提高了0.08 m，其在定位精度上具有优势。

测距误差和不同锚节点个数对基于 RSSI测距定位算法的节点定位精度影响很大，下面分别分析两者的影响。当锚节点个数为10个，测距误差分别由0到30%的平均定位误差如图3所示。由图3可以看出，在较小的测距误差下，BA、CBA、MA-BA、CA-BA的平均定位误差几乎接近于0，能达到较高的定位精度。但随着测距误差的不断增大，不同算法间的平均定位误差的差异开始明显变大，CA-BA算法由于引入了元胞自动机的思想，并且采用了改进的元胞RCS小生境技术和灾变机制，避免了算法陷入局部最优值，增强了算法的全局搜索能力，使得其性能优于 BA算法、CBA算法以及CA-BA算法。当测距误差大于10%以后，BA和CBA算法的平均定位误差大幅增长，MA-BA的算法虽然变化平缓但误差值也大于CA-BA算法，由此可见，CA-BA算法的容错能力和稳定性都较强。

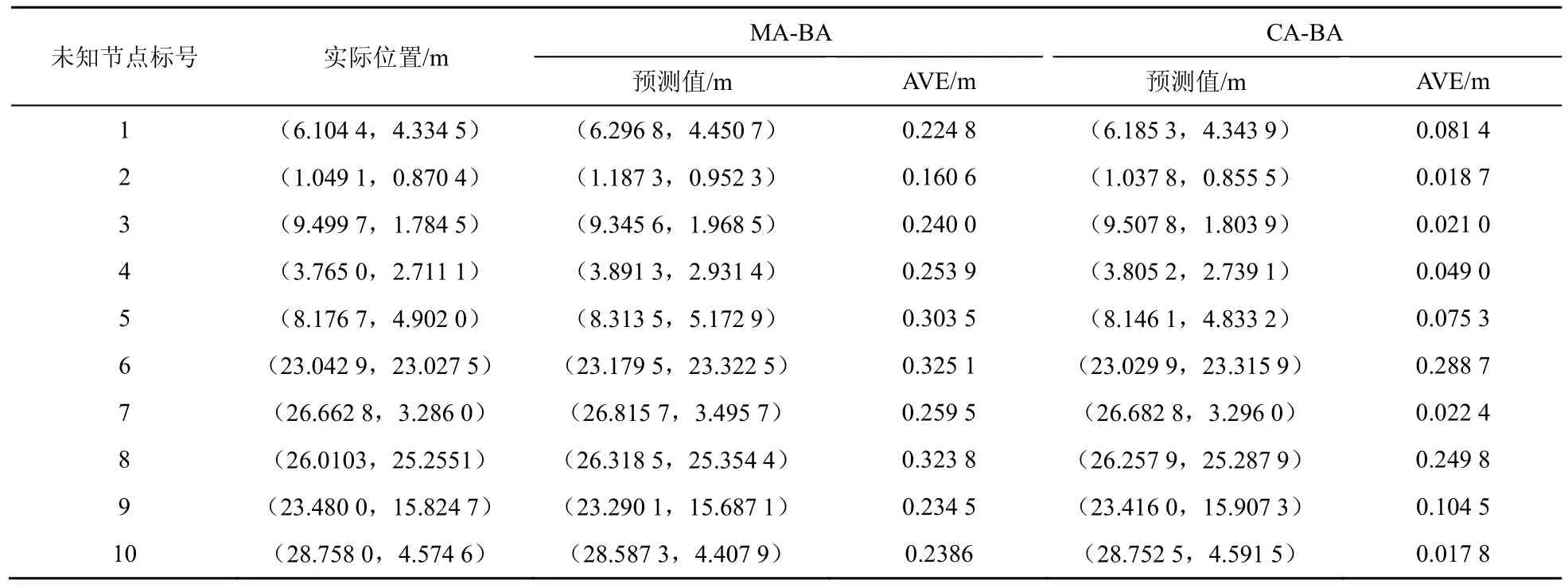
表3 未知节点预测的具体数值比较

图3 测距误差对定位性能的影响

在测距误差固定为10%的情况下，锚节点个数由4个增加到10个，不同算法的平均定位误差的情况如图4所示。由图4可以看出，在相同锚节点个数的情况下，CA-BA算法的平均定位误差明显小于BA算法、CBA算法以及MA-BA算法，精度较高。从整体趋势看，随着锚节点个数的增加，CA-BA算法的整条曲线变化缓慢，可以利用较少的锚节点来实现高精度的节点定位预测。由此可见，在相同的定位精度要求下，CA-BA算法可以使用较少的硬件设备，节约成本，应用前景广泛。

图4 锚节点个数对定位性能的影响

3.2 实际测试分析

为了进一步验证 CA-BA算法在实际使用中的效果，本文通过在实际环境的定位实验来验证算法的性能，测试中采用CC2530模块搭建WSN定位实验平台，RSSI的读取如参考文献[15]方法所示，通过将 RSSI转换为距离值。实验中使用8个锚节点（ T1～ T8）分布在边长为6 m的正方形边界上，将该正方形区域均分成九宫格，对每个格子的中间点进行定位测试，如图5所示，实测如图6所示。

图5 定位实验点布置

图6 定位实验点实测

将实验结果与参考文献[15]中的改进PSO算法进行对比，定位误差如图7所示。由图7可见，本文所提出的CA-BA算法的平均误差在0.4 m左右，改进PSO算法的平均定位误差为0.5 m左右，CA-BA定位效果要优于改进PSO算法的性能，实验结果表明本文所提出的 CA-BA算法在后期的寻优精度上有较大的提高。

图7 锚节点为8时平均误差对比

表4给出了本文CA-BA算法和改进PSO算法的定位结果平均误差的均方根值。由表4可知，在8个锚节点的情况下，改进的PSO的均方根值为0.013 0，本文CA-BA算法的均方根值为0.001 1，由结果可知本文所提 CA-BA算法性能有较大提高。

表4 定位实验误差均方根值

4 结束语

在本文中，首先介绍了基本 BA算法在开发和探索能力上性能较差，较易陷入局部极值而失去种群多样性的探索，据此提出了CA-BA算法，将元胞自动机的思想应用到 BA算法中，并采用了改进的元胞RCS小生境技术和灾变机制，使元胞个体能够较快地跳出局部极值从而避免早熟现象，提高了算法的进化效率，能够更快地收敛到全局最优解。通过对6个标准函数的仿真测试，并与BA算法、CBA算法以及MA-BA算法进行对比，验证了 CA-BA算法在寻找全局最优解和收敛速度方面有很大的提高，并相对其他算法有所改善。将元胞蝙蝠算法应用到无线传感器网络节点定位上，由仿真分析可以看出，在其他因素相同的情况下，测距误差对 CA-BA算法的影响较小，并且其能在较少的硬件设备的情况下达到所要求的定位精度；由测试分析可以看出，CA-BA算法定位的平均误差较小，在定位精度上具有优势。

[1] PENG L J, LI W W. The Improvement of 3D wireless sensor network nodes locolization[C]//26th IEEE Chinese Control and Decision Conference, May 31-June 2, 2014, Changsha, China.New Jersey: IEEE Press, 2016: 4873-4878.

[2] 方震, 赵湛, 郭鹏, 等. 基于 RSSI测距分析[J]. 传感技术学报, 2007(11): 2526-2530.FANG Z, ZHAO Z, GUO P, et al. Analysis of distance measurement based on RSSI[J]. Chinese Journal of Sensors and Actuators, 2007, 20(11): 2526-2530.

[3] 焦磊, 邢建平, 张军, 等. 一种非视距环境下具有鲁棒特性TOA无线传感网络定位算法[J].传感技术学报,2007, 20(7):1625-1629.JIAO L, XING J P, ZHANG J, et al. A new NLOS TOA-based wireless sensor network localization algorithm with robust character[J]. Chinese Journal of sensors actuators, 2007, 20(7): 1625-1629.

[4] 刘长平,叶春明. 具有混沌搜索策略的蝙蝠优化算法及性能仿真[J]. 系统仿真学报, 2013, 25(6): 1183-1188, 1195.LIU C P, YE C M. Bat algorithm with chaotic search strategy and analysis of its property[J]. Journal of System Simulation,2013, 25(6): 1183-1188, 1195.

[5] 赖锦辉. 基于蝙蝠优化算法的无线传感器网络节点定位研究[J].计算机测量与控制, 2014, 22(8): 2709-2712.LAI J H. Research on nodes localization method for wireless sensor networks based on bat optimization algorithm[J]. Computer Measurement & Control, 2014, 22(8): 2709-2712.

[6] 尚俊娜, 刘春菊, 岳克强, 等. 多智能体蝙蝠算法在无线传感器中的应用[J]. 传感技术学报, 2015, 28(9): 1418-1424.SHANG J N, LIU C J, YUE K Q, et al. The multi-agent bat algorithm applied to wireless sensor network[J]. Chinese Journal of Sensors and Actuators, 2015, 25(9): 1418-1424.

[7] 朱大林, 詹腾, 张屹, 等. 多策略差分进化的元胞多目标粒子群算法[J]. 电子学报, 2014, 42(9): 1831-1838.ZHU D L, ZHAN T, ZHANG Y, et al. Cellular multi-objective particle swarm algorithm based on multi-strategy differential evolution[J]. Acta Electronica Sinica, 2014, 42(9): 1831-1838.

[8] 张屹, 万兴余, 郑小东, 等. 基于正交设计的元胞多目标遗传算法[J]. 电子学报, 2016, 44(1): 87-94.ZHANG Y, WAN X Y, ZHENG X D, et al. Cellular genetic algorithm for multiobjective optimization based on orthogonal design[J]. Acta Electronica Sinica, 2016, 44(1): 87-94.

[9] YANG X S. A new metaheuristic bat-inspired algorithm[J].Nature Inspired Cooperative Strategies for Optimization,2010(284): 65-74.

[10] 石杨. 元胞粒子群优化算法及其在柔性作业车间调度中的应用[D]. 武汉: 华中科技大学, 2010: 8-10.SHI Y. A thesis submitted in partial fulfillment of the requirements for the degree of master of engineering[D]. Wuhan: Huazhong University of Science and Technology, 2010: 8-10.

[11] 张俞. 元胞遗传算法的研究[D]. 江西: 南昌航空大学, 2009:37-41.ZHANG Y. Research for cellular genetic algorithm[D]. Jiangxi:Nanchang Hangkong University, 2009: 37-41.

[12] 李新鹏, 张超勇, 高亮, 等. 基于元胞粒子群算法的数控切削参数优化[J]. 计算机工程与应用, 2014, 50(2): 252-257.LI X P, ZHANG C Y, GAO L, et al. NC cutting parameter optimization based on cellular particle swarm optimization algorithm[J]. Computer Engineering and Applications, 2014, 50(2):252-257.

[13] 鲁宇明, 陈殊, 黎明, 等. 自适应调整选择压力的灾变元胞遗传算法[J]. 系统仿真学报, 2013, 25(3): 436-444.LU Y M, CHEN S, LI M, et al. Self-adaptive cellular genetic algorithms with disaster based on selection pressure[J]. Journal of System Simulation, 2013, 25(3): 436-444.

[14] 詹杰, 刘宏立, 刘述钢, 等. 基于RSSI的动态权重定位算法研究[J]. 电子学报, 2011, 39(1): 82-88.ZHAN J, LIU H L, LIU S G, et al. The study of dynamic degree weighted centroid localization algorithm based on RSSI[J]. Acta Electronic Sinica, 2011, 39(1): 82-88.

[15] 尚俊娜, 盛林, 程涛, 等. 基于 LQI权重和改进粒子群算法的室内定位方法[J]. 传感技术学报, 2017, 30(2): 284-290.SHANG J N, SHENG L, CHENG T, et al. The indoor localization based on LQI weight and improved particle swarm optimization algorithm[J]. Chinese Journal of Sensors and Actuators,2017, 30(2): 284-290.

Wireless sensor network nodes localization method based on cellular automata bat algorithm

MENG Kailu1, YUE Keqiang2, SHANG Junna1
1. College of Telecommunication Engineering, Hangzhou Dianzi University, Hangzhou 310018, China 2. College of Electronic Information, Hangzhou Dianzi University, Hangzhou 310018, China

To further enhance the location precision of unknown nodes and solve the node location error in wireless sensor network, a location method based on cellular automata bat algorithm was presented. Mixed the idea of cellular automata and the bat algorithm and drawed into the cellular RCS niche technique and disaster mechanism, the algorithm could jump out of local optimum and increase the convergence speed. In order to verify the feasibility and efficiency, the proposed algorithm was verified through simulation of several benchmark functions. Then the algorithm implemented the CA-BA to node location prediction to increase the precision of the unknown node location. In the measured experiment, the results show that the proposed algorithm has higher accuracy compared to the improved PSO algorithm, which average localization error is less than 0.5m.

WSN, node localization, cellular automata, bat algorithm, accuracy

s:The National Natural Science Foundation of China (No.11603041), Open Funds by Guangxi Key Laboratory of Precision Navigation Technology and Application, Guilin University of Electronic Technology (No.DH201714), “Electronic Science and Technology” of the Most Important Subject Open Funds in Zhejiang Province (No.GK13020320003/004), Research and Innovation Fund for Graduate Students of Hangzhou Dianzi University(No.ZX170603308034)

TP393

A

10.11959/j.issn.1000−0801.2017311

2017−09−02；

2017−09−26

岳克强，290035613@qq.com

国家自然科学基金资助项目（No.11603041）；广西精密导航技术与应用重点实验室开放基金资助项目（No.DH201714）；浙江省“电子科学与技术”重中之重学科开放基金资助项目（No.GK13020320003/004）；杭州电子科技大学研究生科研创新基金资助项目（No.ZX170603308034）

孟凯露（1993−），女，杭州电子科技大学通信工程学院硕士生，主要研究方向为智能算法。

岳克强（1984−），男，博士，杭州电子科技大学电子信息学院讲师，主要研究方向为进化计算、通信信号处理。

尚俊娜（1979−），女，博士，杭州电子科技大学通信工程学院副教授，主要研究方向为通信信号处理、智能算法。