基于比例边界有限元的温度断裂研究

钟 红，贺 帅，李红军

（1.大连理工大学建设工程学部，辽宁省大连市 116024；2.中国水利水电科学研究院，北京海淀区 100044）

基于比例边界有限元的温度断裂研究

钟 红1，贺 帅1，李红军2

（1.大连理工大学建设工程学部，辽宁省大连市 116024；2.中国水利水电科学研究院，北京海淀区 100044）

温度荷载是导致结构开裂、影响结构稳定性的一个重要因素。本文基于比例边界有限元方法提出了温度断裂分析的模型。利用比例边界有限元法求解结构温度场，结构分析中的温度荷载表示为径向坐标的函数并等效为若干项幂级数之和，基于线性叠加原理求解结构响应。该模型的特点包括：只需离散求解域的边界从而降低了求解问题的维数；在求解裂缝尖端的温度场、位移场和应力场时均可获得半解析解，应力强度因子求解精度高。通过多个板承受温度荷载的温度场分析与结构分析可以看出利用较少的网格即可获得较高的精度，模拟所得的应力强度因子随着裂缝长度的增长而增长，并且本模型计算的应力强度因子与现有文献结果一致，证明了本模型的有效性。

温度荷载；比例边界有限元；温度场；应力强度因子

0 引言

随着水电战略的实施，高大混凝土坝不断地建设，混凝土坝温度断裂问题也越来越突出，特别是大体积混凝土坝，由混凝土水化热、外界气温、浇筑温度、太阳辐射等引起的温度荷载经常会引起较大的拉应力，其数值甚至可能超过混凝土的抗拉强度，从而导致混凝土产生裂缝，破坏大坝的整体性，降低耐久性，危及坝体的安全。国内外学者开展了大量的研究，在温度场与温度裂缝扩展的仿真模拟方面取了一些进展，如Wilson编制了求解大体积混凝土结构的二维温度场的有限元程序DOT-DI-CE，并用该程序计算了德沃歇克（Dworshak）坝的温度场；随后美国陆军工程师对有限元程序DOT-DICE进行修改，并利用此程序计算大体积混凝土结构的温度场，将研究的成果应用到Willow Creak大坝的温度场分析中，得到了不同时期的温度场数据，与实际情况十分符合[1]；程井与常晓林等人[2]采用无单元伽辽金法求解水工结构应力强度因子及仿真模拟温度裂缝扩展过程，在计算过程中不需要重新剖分网格，可以自由调整节点分布，能够动态地追踪裂缝扩展且单元边界不影响裂缝扩展路径；Duflot M采用扩展有限元方法求解了裂纹板的应力强度因子及温度场，得到了精确的结果[3]。

对温度断裂的研究包括温度场求解和断裂场模拟两方面。通用的有限元法对于断裂过程的模拟存在比较大的困难。比例边界有限元法是一种新型的半解析的数值方法，它继承了边界元（BEM）和有限元（FEM）方法的优点，只需对边界进行离散，不需要对整个区域进行离散，与边界元相对比，比例边界有限元不需要基本解，而与有限元相比，其需要较少的节点，可以提高计算效率[4]。在处理断裂问题时具有突出优势，无需基本解和奇异积分，在开裂方向上位移和应力具有解析解，因此从奇异应力模态直接提取应力强度因子精度很高。宋崇民提出了在温度荷载作用下广义应力强度因子的定义和计算方法，能得到整个区域准确的温度场、位移场及应力场。

本文将比例边界有限元方法引入混凝土结构的温度断裂分析，开展了结构的热分析与结构分析，并以多个算例验证了模型的有效性。

1 基本原理

1.1 温度场求解

本文基于比例边界有限元法（Scaled Boundary Finite Element Method，SBFEM）开展温度场分析和结构分析。该方法的控制方程的推导和求解见文献[5]，此处不再赘述。基于虚功原理[6]或矩阵函数法[4]进行推导，可以得到二维情况下求解温度场的控制方程：

其中[E0t]、[E1t]、[E2t]为单元边界上的系数矩阵，上标t代表温度场，以便于与结构分析中的相应矩阵区分。该系数矩阵只和单元几何构型和材料参数有关式（2）～式（4），其计算和组装与有限元法类似，式中k为热传导系数。

径向内部热源为：

式（1）、式（5）可联立表示成一阶常微分方程：

式中，[Z]是哈密顿系数矩阵：

比例边界有限元法的单元刚度矩阵的组装过程与有限元法相同，即先求得各个单元的刚度矩阵，而后将所有刚度阵进行组装即可得到整体刚度矩阵，将方程（8）代入式（6）中求得：

式中，ct是积分常数，可以由边界温度T（ξ=1）计算得到：

用形函数N（η）对T（ξ）插值，求出全域的温度场T（ξ，η）：

1.2 位移场求解

比例边界有限元法中的位移场在径向可以获得解析解，从相似中心O出发沿着径向线，ξ处的位移为{u（ξ）}，径向η是一个常量，因此只需要环向的插值形函数和{u（ξ）}即可表达域内任意点的位移{u（ξ，η）}为：

应力为：

式中，[D]是材料的弹性矩阵；B1（η）和B2（η）是应变位移矩阵[7]。

用位移表达的比例边界有限元方法的控制方程[8-9]，如下所示：

其中[E0]、[E1]、[E2]为单元边界上的系数矩阵，只和单元的几何构型和材料参数有关，计算和组装与传统的有限元方法类似。{F（ξ）}为是外部荷载。若外部荷载只包含温度荷载，则{F（ξ）}可表示为如下形式：

式中，d为计算温度场时的特征值的相反数；| J（η）|为雅各比矩阵的行列式。

内部等效节点力为：

式中，{q0（ξ）}为由初始温度应力产生的内部节点力：

温度引起的初始应力{σ0}可以由下式推得[11]：

式中，T为式（11）求得的温度场；{β}是与温度相关的系数。

式中，v为泊松比；α为热膨胀系数。

对式（12）进行求解，可以求得位移为：

对位移u{ξ}进行插值得到全域的位移{u（ξ，η）}，并通过位移法可以求得应力强度因子[13]。

2 数值算例

为了验证模型的有效性，下文分析了带裂缝平板的温度场、位移场、应力强度因子。

2.1 各向同性等温裂缝板承受温度荷载

考虑如图1（a）所示的含中心裂缝的等温裂缝平板，尺寸为2W×2W，中心裂缝长度2a，材料的弹性模量E=2.184×105Pa，泊松比ν=0.3，热膨胀系数α=1.67×10-5/℃。图中给出了板的温度边界条件，T代表温度值，hq代表绝热。为与文献结果比较，采用平面应变假定进行分析。考虑到结构和荷载的对称性，取1/2结构进行分析。整个模型离散为45个比例边界有限单元（图2）。

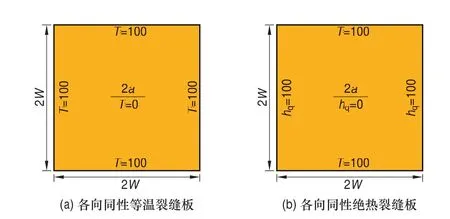
图1 带裂缝板（单位：℃）Fig. 1 Plate fracture

图3给出了板的温度云图，其温度值从裂缝处开始向结构四周逐渐增大，在板顶部、底部与右侧达到100℃，这一结果与参考文献[12]采用扩展无网格伽辽金法得到的结果相符。图4为板的位移云图，水平位移值从左侧向右侧两角逐渐增大，在两角处达到最大值为0.24cm；竖直方向位移值分别在板的左上角和左下角处达到最大和最小，其值分别为0.45cm与0.05cm。

图2 网格图Fig. 2 Polygon mesh

图3 温度场（单位：℃）Fig. 3 Temperature field

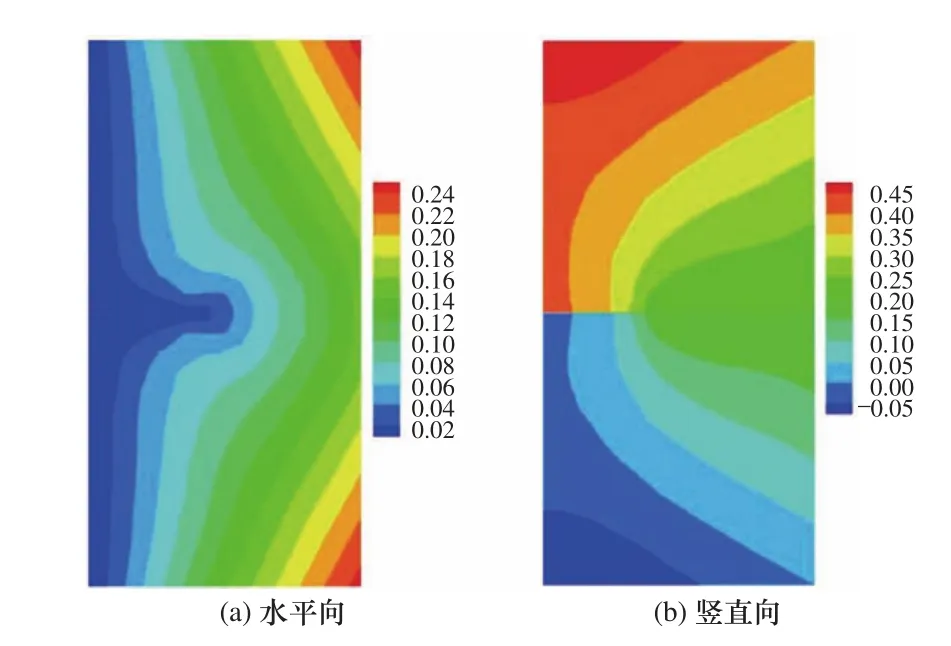
图4 位移场（单位：cm）Fig. 4 Displacement field

2.2 各向同性绝热裂缝板承受温度荷载

考虑如图1（b）所示的含中心裂缝的绝热裂缝平板，板的尺寸是2W×2W，中心裂缝长度2a。材料的属性同3.1节。图中给出了板的温度边界条件，T代表温度值，hq=0代表绝热情况。由于结构是对称的，所以取半结构进行分析。采用平面应变假定。整个模型离散为45个比例边界有限单元（图5）。

表1 等温裂缝板的应力强度因子对比（KI*）Tab. 1 Thermal insulation plate crack stress intensity factor of the contrast（KI*）

图6给出了结构的温度云图，其温度值从板的低端向顶端逐渐增大，在板低端与顶端的温度值分别为-100℃与100℃，并与扩展无网格伽辽金法[12]（XEFG）所示温度云图相同；图7给出了结构的位移云图，裂缝上部分板的水平位移从左下部向右上部逐渐增加，在右上角处达到最大值为0.20cm；下部分板的水平位移从左上部向右下部逐渐减小，在右下角处达到最小值为-0.20cm。板的左边角处的竖向位移值最大，其值为0.1cm。

图5 网格图Fig. 5 Polygon mesh

图6 温度场（单位：℃）Fig. 6 Temperature field

图7 位移场（单位：cm）Fig. 7 Displacement field

表2 绝热裂缝板的应力强度因子对比（KII*）Tab. 2 Thermal insulation plate crack stress intensity factor of the contrast（KII*）

2.3 各向同性等温斜裂缝板承受温度荷载

考虑如图8所示的含中心裂缝的等温斜裂缝平板，板的尺寸是2W×2L，θ1=0℃，θ2=100℃，W=1.0m，L=2.0m，a=0.3m，β=30o，材料参数为弹性模量E=2.184×105Pa，泊松比为0.3，热膨胀系数为1.67×10-5/℃，采用平面应变问题分析。

图9给出了结构的温度云图，其温度值从裂缝处开始向结构四周逐渐增大，裂缝处与四周的温度值分别为0℃与100℃，并与扩展无网格伽辽金法[12]（XEFG）中的温度云图相符。图10给出了结构的位移云图，水平位移从板的左边向后边逐渐增大，在右边端角达到最大值为0.4cm。竖直向位移从板的低边向顶边逐渐增大，在板底边与定边的竖直向位移值分别为0.05cm与0.75cm。本文方法计算的应力强度因子KI*为0.296，KII*为0.047，扩展无网格伽辽金法[14]（XEFG）所得的KI*为0.294，KII*为0.045，其相对误差分别为0.6%、4.2%。

图8 网格图Fig. 8 Polygon mesh

图9 温度场（单位：℃）Fig. 9 Temperature field

图10 位移场（单位：cm）Fig. 10 Displacement field

3 结束语

本文基于比例边界有限元方法，提出了结构在温度荷载作用下的线弹性断裂分析模型，得到了裂缝的扩展过程和结构的整体响应。首先利用比例边界有限元方法求解结构的温度场，在结构分析中将温度场转化为与径向坐标有关的温度荷载{F（ξ）}，代入结构分析的比例边界有限元方法求解格式，求出位移场、应力场和应力强度因子。通过三个承受温度荷载的板的算例验证了本模型的计算精度，且可看出利用较少的网格即可获得很高的精度。综上，本文模型是求解结构温度断裂分析的一种高精度高效率的数值方法。

[1] Tatro S，Schrader E. Thermal analysis for RCC—a practical approach[C]//Roller compacted concrete III. ASCE，1992：389-406.

[2] 程井，常晓林，周伟，等. 基于无单元伽辽金法的水工结构温度应力及温度裂纹扩展计算[J]. 四川大学学报：工程科学版，2009（4）.CHENG Jing，CHANG Xiaolin，ZHOU Wer，et al. Simulation of thermal stress and crack propagation in Hydraulic structures based on EFGM[J]. Journal of Sichuan University: Applied Mechanics & Materials，2009 （4）.

[3] Duflot M. The extended finite element method in thermoelastic fracture mechanics[J]. International Journal for Numerical Methods in Engineering，2008，74（5）：827-847.

[4] Song C，Wolf J P. The scaled boundary finite-element method—alias consistent infinitesimal finite-element cell method—for elastodynamics[J]. Computer Methods in applied mechanics and engineering，1997，147（3）：329- 355.

[5] Song C. Analysis of singular stress fields at multi-material corners under thermal loading[J]. International journal for numerical methods in engineering，2006，65（5）：620-652.

[6] Deeks A J，Wolf J P. A virtual work derivation of the scaled boundary finite-element method for elastostatics[J]. Computational Mechanics，2002，28（6）：489-504.

[7] Song C. A matrix function solution for the scaled boundary finiteelement equation in statics[J]. Computer Methods in Applied Mechanics and Engineering，2004，193（23）：2325-2356.

[8] Song C，Wolf J P. Body loads in scaled boundary finiteelement method[J]. Computer methods in applied mechanics and engineering，1999，180（1）：117-135.

[9] Lin Z，Liao S. The scaled boundary FEM for nonlinear problems[J]. Communications in Nonlinear Science and Numerical Simulation，2011，16（1）：63-75.

[10] Li C，Ooi E T，Song C，et al. SBFEM for fracture analysis of piezoelectric composites under thermal load[J]. International Journal of Solids and Structures，2015，52：114-129.

[11] Song C，Tin-Loi F，Gao W. A definition and evaluation procedure of generalized stress intensity factors at cracks and multi-material wedges[J]. Engineering Fracture Mechanics，2010，77（12）：2316-2336.

[12] Bouhala L，Makradi A，Belouettar S. Thermal and thermomechanical influence on crack propagation using an extended mesh free method[J]. Engineering Fracture Mechanics，2012，88：35-48.

[13] Tsang D K L，Oyadiji S O，Leung A Y T. Two-dimensional fractal-like finite element method for thermoelastic crack analysis[J]. International Journal of Solids and Structures，2007，44（24）：7862-7876.

2017-03-23

2017-05-19

钟 红（1981—），女，副教授，主要研究方向：主要从事混凝土结构静动力分析研究。E-mail：hzhong@dlut.edu.cn

贺 帅（1988—），男，硕士，主要研究方向：主要从事混凝土结构温度断裂分析研究。E-mail：1255536943@qq.com

李红军（1988—），男，高级工程师，主要研究方向：主要从事大坝静动力分析研究。E-mail：lijunli1995@163.com

Thermal fracture analysis based on the Polygon Scaled boundary finite element method

ZHONG Hong1，HE Shuai1，LI Hongjun2
（1.Faculty of Infrastructure Engineering，Dalian 116024，China；2.China Institute of Water Resources and Hydropower Research，Beijing 100044，China）

Thermal load can lead to cracking of structure and thus seriously influence the stability of the structure. A numerical model for the thermal fracture analysis is presented based on the Scaled Boundary Finite Element Method（SBFEM）. The temperature distribution is solved via the SBFEM，then the corresponding thermal load is divided into several items in the form of power functions，and the structural response is further obtained based on the principle of linear superposition. In the presented model，only the boundary of the structure is discretized，the temperature，displacement and stress fields can be obtained semi-analytically，thus the stress intensity factors are solved with high precision.Through multiple plate under temperature load，temperature field analysis and structure analysis can be seen that using fewer grid can obtain higher precision.Simulation results of stress intensity factor as the growth of the crack length increases，and the stress intensity factor consistent with the existing literature，which demonstrates the effectiveness of the model.

thermal load； the Scaled boundary finite element method； temperature fields； stress intensity factor

TV313

A学科代码：130.1545

10.3969/j.issn.2096-093X.2017.03.013

国家自然科学基金（51579033）；国家重点研发计划（2016YFB0201000，2016YFC0401600）。