寻找数学有趣的密码

文︳徐 晟

寻找数学有趣的密码

文︳徐 晟

很多人都说数学是枯燥的，乏味的学科。这是因为数学是形式科学的一种，它抽象、严密，越到高一级知识越明显，学生不易接受。所以，教学时一定要将数学知识通俗化、趣味化，才能让学生易于理解。但现实教学情况不容乐观，因此许多学生学数学时感到恐惧和焦虑。

比如，中学数学中“无理数”概念的学习。这个概念可是引发了数学史上的第一次数学危机，它是抽象的、难理解的。如果教学中不作通俗化的处理，学生根本就不知道这个概念是怎么产生的，有什么本质属性。因此，教材是这样编排的（如图）。

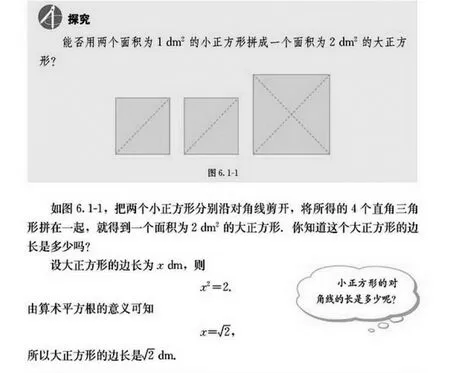
为什么学习数，要从几何开始？这样设计，是符合历史，也符合逻辑的。因为，无理数的发现，正是从研究正方形的对角线与边的关系中产生的。

历史上，古希腊数学家毕达哥拉斯将数学知识运用得纯熟之后，觉得不能只满足于用来算题解题，于是他试着从数学领域扩大到哲学，用数的观点去解释世界。经过一番刻苦实践，他提出“万物皆为数（指有理数）”的观点：数的元素就是万物的元素，世界是由数组成的，世界上的一切没有不可以用数来表示的，数本身就是世界的秩序。

但是，毕达哥拉斯学派的弟子希帕索斯发现了一个惊人的事实，一个正方形的对角线与其一边的长度是不可公度的（若正方形的边长为1，则对角线的长不是一个有理数）。这一不可公度性与毕氏学派的“万物皆为数”的观点大相径庭。这一发现使该学派领导人惶恐，认为这将动摇他们在学术界的统治地位，于是极力封锁该真理的流传。希帕索斯被迫流亡他乡。不幸的是，在一条海船上还是遇到毕氏门徒。最终他被毕氏门徒残忍地投入了水中杀害。

希帕索斯的发现，第一次向人们揭示了有理数系的缺陷，证明了它不能同连续的无限直线等同看待，有理数并没有布满数轴上的点，在数轴上存在着不能用有理数表示的“孔隙”。而这种“孔隙”经后人证明简直多得不可胜数。于是，古希腊人把有理数视为连续衔接的那种算术连续统的设想彻底地破灭了。不可公度的发现，对以后2000多年数学的发展产生了深远的影响，促使人们从依靠直觉、经验转向依靠证明，推动了公理几何学和逻辑学的发展，并且孕育了微积分思想。人们为了纪念希帕索斯这位为真理而献身的可敬学者，就把不可公度的量取名“无理数”——这就是无理数的由来。

由无理数引发的数学危机一直延续到19世纪下半叶。1872年，德国数学家戴德金从连续性的要求出发，用有理数的分割来定义无理数，并把实数理论建立在严格的科学基础上，从而结束了无理数被认为无理的时代，也结束了持续2000多年的数学史上的第一次大危机。

由此看来，无理数来之不易，学习无理数概念时，让学生知道这段历史，既可以帮助他们更好地理解概念，也增添了趣味性。

你是有心人，教学可以从这一点出发，学习概念后，再让学生从数学美的角度体验数学的有趣。

我们来看看与无理数有关的美妙的式子，趣味会来得更足。比如这个式子：

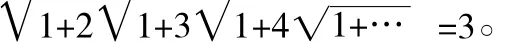
这个优美的式子来自印度数学奇才拉马努金。他曾经深入地研究了形如上式的无穷根式并得到了这个神奇的结果。传说拉马努金曾经把这个结果放在《印度数学会刊》上征集证明，结果数月内无人能应。

如果上式还不足以让人惊叹，那再看看这个：

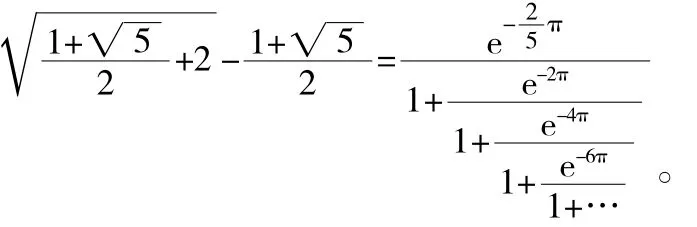
这个绝美的公式不仅将圆周率和e联系起来，还将黄金分割数也包含在内。它的发现者，仍然是印度数学奇才拉马努金。1913年，来自南印度的小职员拉马努金，给当时32岁就已经执掌英国数学界牛耳的哈代去了一封长达9页的信，信中附带了120条他发现的公式，上面这个公式就是其中的一条。这条公式令哈代完全摸不着头脑，他从没见过这样的公式，连稍微接近点的都没有！但是哈代确信这个公式是对的，因为没有人能有这样的想象力去编造这样漂亮的公式。果然不久之后，数学家们就严格地证明了这个公式，它和谐而又气势磅礴的形式令每一个初次见到它的人都会为之悸动！借用哈代的一句话：“这个公式完全打败了我，我无法确信世界上居然还会有这种东西存在！”

数学就是那么巧妙，圆周率和e都是无理数，那你再看看它——eπi+1=0。这就是受到我们万世敬仰的欧拉公式。它将数学里最重要的几个数字联系到了一起：两个无理数：自然对数的底e，圆周率π；两个单位：虚数单位i和自然数的单位1；以及被称为人类伟大发现之一的0。数学家们评价它是“上帝创造的公式”。

历史上的欧拉是一位全才数学家，同时也是一名虔诚的教徒，笃信上帝的存在。据说有一次俄国的叶卡捷琳娜二世邀请狄德罗访问她的宫廷，而狄德罗是一名不折不扣的无神论者。不久，叶卡捷琳娜二世就厌倦了狄德罗那喋喋不休的无神论说教之词，让欧拉来好好教训他一顿。欧拉开门见山地质问道：“eπi+1=0，所以上帝存在，请回答！”结果不懂数学的狄德罗被弄得一头雾水，无言以对。

你看，本来枯燥难懂的无理数概念，经过挖掘，前后多了许多有趣的事情。学习前，可以了解历史故事，学习后，可以欣赏美妙的公式。

也许你会问，欣赏过后呢？我们能否自己创造？最后看看这个例子，你就知道答案了。

话说世人皆知勾三股四弦五，而鲜有人知道这个简单的等式：33+43+53=63。这个完美的式子可以在上述提到的英国数学家哈代所著的《数论导引》中找到，它是一类三次不定方程最简单的特解。学习勾股定理时，我们都会写32+42=52。然而写完就了事。实际上，稍微类比运算一下，就能得出33+43+53=63。可是，大家都没有想到它，与数学有趣的密码失之交臂，多么令人遗憾！

（作者单位：长沙市雅礼中学）