基于端元变化的两种混合像元分解算法比较研究

(西华师范大学 国土资源学院,四川 南充 637009)

基于端元变化的两种混合像元分解算法比较研究

段金亮,王 杰,文星跃
(西华师范大学 国土资源学院,四川 南充 637009)

光谱混合分析对提高遥感影像分类具有重要意义,其中端元变化处理是提高解混精度的关键。目前,许多算法被用来解决端元变化,但仍存在一些问题有待解决，如算法运行效率慢、忽略端元的高阶交互、像元空间邻城信息缺失。结合IDL和MATLAB混合编程,利用确定性模型中的交替最小角度法和统计性模型中考虑高阶项的非线性算法对Hyperion影像进行端元变化解混,再利用概率松弛标记法对像元补充空间邻域信息。试验结果表明:当某种地物类别所占面积较大时,确定性与统计性模型都能获得较高的解混精度;当地物类别所占面积较小时,确定性模型的解混精度高于统计性模型;补充像元空间邻域信息对解混结果有很好的校正。

Hyperion影像;端元变化解混;IDL与MATLAB混合编程;交替最小角度法;非线性混合模型

1 引言

由于地物的复杂多样性和电磁辐射传输过程中的各种环境因素[1],遥感图像中普遍存在混合像元。混合像元的光谱包含多种地物,如果将其归为一类,势必会造成分类误差增大、分类精度下降,因此光谱混合分析对遥感影像分类具有重要意义。传统的光谱分解技术[2]主要假设某一像元的光谱是由有限的几种地物组成,其光谱曲线是按照某种函数关系和比例混合而成,进而分析光谱混合方式,计算混合像元中包含的光谱成分与相应比例。线性混合模型(LMM)[3]中,端元通常被假定在整个影像中是固定的,这显然是一个简化过程。因为在许多情况下,端元光谱是沿着图像变化,引起光谱变异性或端元变异性[4,5]。光谱变异性已被确定为丰度估计的相关误差源,引起了高光谱研究群体日益增长的兴趣[4,5]。国内外学者提出了许多算法来描述端元的变化,它们被分为两个主要类别：第一类是将每种类别视为已知的光谱库[6,7]或从遥感数据获取的端元束[8,9]来进行解混,此类算法被称为确定性模型,其中最常用的算法是多端元混合光谱分析(MESMA)[10]。第二类则采用统计分布来描述端元的变化,主要包括两个模型,分别是假定端元高斯分布的正态成分模型[11,12]和探索光谱与空间分布的Beta成分模型。

目前虽然有很多算法用来解决端元变化,但是仍存在一些问题有待解决。首先,统计性模型中单纯非线性算法仅考虑端元之间的二阶交互而忽略了高阶项的影响。其次,虽然确定性模型中的MESMA算法很好地处理了端元变化,但MESMA算法是一种穷尽算法,在运算效率上有一定的限制。第三,多数解混算法仅对单个像元光谱进行了优化,忽略了空间邻域信息,导致解混精度减低。针对当前解混算法存在的问题,本文描述了优化的交替最小角度法(确定性模型)来提高程序的运算效率,同时引入了一种考虑高阶项的非线性算法(统计性模型),最后利用一种补充像元空间邻域信息的算法来校正解混精度。本文采用IDL与MATLAB的混合编程,解决了MATALB的功能模块分散、灵活性较差[13]的缺陷,能有效地整合遥感影像处理与数学计算。

2 研究区与遥感影像预处理

研究区选择新疆维吾尔自治区天山中段焉耆盆地,地处85°50′—87°50′E、41°40′—42°20′N,为南天山山脉之间的中生代断陷盆地,海拔高程1050—1200m,是一个典型的绿洲—荒漠交错地区[14]。研究区具体的经纬度范围为86°10′—86°50′E、42°20′—42°60′N,高程变化可忽略不计。焉耆盆地属于南北疆过渡的大陆荒漠性气候[15],多年平均气温8.4℃,年降水量50—80mm,年蒸发量2000.5—2449.7mm[16],水土资源丰富、光热条件充分,是新疆农牧业生产的主要基地之一。研究所选用的数据为从美国USGS网站获取的L1R格式Hyperion影像,数据成像时间为2006年7月18日,影像编号EO1H1430302006199110PX,无云。

高光谱影像预处理过程:删除Hyperion影像立方体中定标质量较差的波段,剩余176个波段,分别为8—57(426—926nm)、79—120(933—1346nm)、128—166(1427—1810nm)、179—223(1942—2385nm)。由于Hyperion传感器所用的CCD阵列辐射标定导致影像中存在明显的坏线，我们对已选择的176个波段逐波段进行检查,记录每个波段坏线的列号,采用坏线所在行列左右相邻的均值对该波段亮度值(DN)进行插值修复,如可见光(VNIR)等。其中,可见光(VNIR)波长范围为400—1000nm,辐射定标值为40W·(m2srμm)-1,短波红外(SWIR)波长范围900—2500nm,辐射定标值为80W·(m2srμm)-1。我们将所有的VNIR波段和SWIR波段分别除以40和80所得图像合并,得到绝对辐射值图像。由于Hyperion传感器是推扫型成像光谱仪,对面阵CCD器件上的上万个探测元件进行逐一标定很困难,导致Hyperion影像多数波段不同程度地存在许多条纹。本文采用 “全局去条纹”方法对Hyperion影像进行条带去除，将Hyperion影像与ALI影像分别进行波段合并,得到了新的两幅影像。地物反射易受大气和光照等因素的影响,因此对Hyperion影像进行大气校正,大气模型设置为中纬度夏季(MLS),水汽校正波段为1135nm,初始可见性为37,光谱打磨步长为7,气溶胶反演为None,其他参数设置为默认值。大气校正后得到的是反射率图像,且反射率值被放大10000倍,因此将结果除以10000。裁剪出研究区影像见图1(封二)，波长对应于TM影像的7波长、4波长、1波长。

运用ALI高空间分辨率影像进行解混精度评价。首先对ALI数据进行辐射定标以生成辐射值,其中Gain与Bias系数参见相关文献[17]。然后进行Gram-Schmit Spectral Sharpening融合,使其具有更高的分辨率(10m空间分辨率)。裁剪出研究区影像,从图2(封二)可见，波长对应于TM影像的7波长、4波长、1波长。同时，为了后续ALI影像监督分类选择样本的需要,下载了Google Earth影像,见图3(封二)。

3 试验方法

3.1 确定性端元变化解混—交替最小角度法(AAM)

线性混合模型(LMM)是遥感影像处理中常用的一种光谱分析模型,主要通过选取特征地物的光谱将其作为端元,然后解混整个遥感影像。全约束最小二乘法(FCLS)[18]是一种被广泛使用的混合像元分解算法,公式为:

(1)

式中,m为端元；ai为像元的丰度；η为一个加性噪声；R为端元的总数。

固定端元在解混时容易受到地物物理特征的变化和大气、光照条件的影响,导致端元光谱变化。此时，FCLS算法就有局限性,因此多端元混合光谱分析算法(MESMA)[10]被提出来处理端元变化。虽然MESMA算法很好地处理了端元变化,但算法的运算效率太低,导致算法的适用性不强。针对MESMA算法的局限性,这里采用交替最小角度算法[19]来提高程序的运算效率。

如果我们将每个光谱认定为d维向量光谱空间[0,1]的点,且假设光谱噪声呈一致性分布,应用最大似然法在线性混合问题中将产生最小二乘问题,这个最小二乘问题等价于数据点x映射到光谱子空间S上的最小欧氏距离。

y=Ps(x)⟺∀z|∈S:‖z-x‖≥‖y-x‖

(2)

如果仅考虑和为1的约束条件,解混问题等价于将目标x通过M中的端元正交投影到超平面H(M)上。重建误差由x到H(M)的正交距离给出,如果我们定义F=M/{mp}=(m1,…mp-1),使用标准几何关系表示这个正交距离:

‖x-PH(M)(x)‖=‖x-PH(F)(x)‖sin(θ)

(3)

其中:θ=min(α,π-α)

3.2 统计性端元变化解混—NL模型

LMM模型假定端元之间是相互独立的,但在遥感影像的获取过程中,电磁波与地物可能存在多次交互,特别是植被与土壤的交互,这样端元就不是纯粹的独立关系。如果以线性混合模型来反演,必然导致解混精度减低，这里采用非线性混合像元分解算法[20]来解决端元变化导致的反演误差。将混合模型分为线性部分、端元的非线性交互项、噪声项三部分,由式(1)得出:

(4)

式(4)中丰度系ar数满足式(1)中的非负与和为1的限制。

非线性混合模型为克服LMM的固定限制提供了有用的替代方案。LMM模型可能不适用于那些包含树木、植被或城市的地区的高光谱图像。对处理这类影像,线性/多项式模型已通过解决双重散射效应显示了有用的结果,但这些模型仅考虑了端元之间的二阶交互而忽略了高阶项的影响,这里采用双线性非线性模型,将式(4)重新改写为：

(5)

其中,残差分量被表示为:

(6)

3.3 像元空间邻域信息处理—PLR聚类法

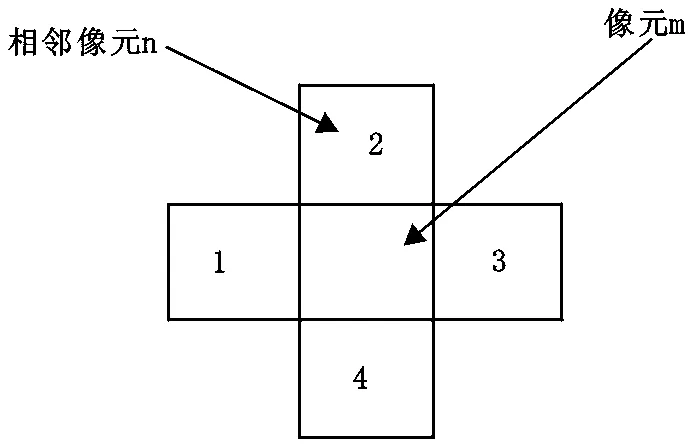
图4 一个像元邻域

多数解混算法仅考虑单个像元的光谱属性,导致图像内的空间关系被忽略,如区域的相关性和纹理,导致解混精度降低。本文引入一种考虑分类图像中隐含的部分空间信息的后处理技术来提高解混精度,这种技术是利用后验的向量与每个分类像元相关联的概率来校正解混结果。

图4表示单个像元m及其直接邻域n,我们认为该像元由m的上方、下方、左侧和右侧的四个像元组成。让其后验概率满足如下公式:

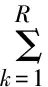
(7)

(8)

用矢量方法表达式(8),得到如下结果:

(9)

根据贝叶斯概率理论,推导出:

(10)

4 试验处理

ALI数据融合后,采用支持向量机算法(SVM)对影像进行分类。根据Google Earth与ALI影像判别研究区主要包括四类,分别是植被、未利用地、建筑用地、水体及其阴影。研究区ALI影像分类参照相关文献[22]选择感兴趣的区和验证样本。SVM算法内置于ENVI软件中,核函数采用径向基函数,核函数值为0.167,惩罚参数为100,金字塔水平设置为1,金字塔重分类阀值设为0.9，结合Google Earth高分辨率影像采取目视解译的方法改正分类错误的像元。由于ALI分类影像的空间分辨率与Hyperion影像的空间分辨率不一致,因此我们采用一个大小为3×3的模板重采样,使其与Hyperion影像的空间分辨率保持一致。其真实覆盖度影像见图5(见封二)。

混合像元解混前,需要建立端元光谱库,这里采用自动端元束(AEB)算法获取4个类别的端元。删除异常的端元后,最终每个类别获取10个端元,建立端元光谱曲线图(图6,见封二)。

在建立端元光谱库后,编写AAM与NL的Matlab解混代码,然后编写IDL通过COM接口调用其程序,这里AAM与NL算法的Matlab代码都是以函数形式给出的,由于本文篇幅限制,因此没有罗列Matlab代码。其中,Matlab的版本为R2009a,32位，IDL版本为8.5,64位，操作系统为Windows 7,64位。在IDL中分别编写AAM和NL调用及输出结果的代码,分别命名为AAM.pro和NL.pro。其中,AAM.pro部分代码为：

openr,lun,′C:UsersAdministratorDesktopdataSpectral

Library.txt′,/get—lun

end=fltarr(40,num—bands)

readf,lun,end

free—lun,lun

end1=reform(transpose(end(0:9,*)),10,num—bands)

end2=reform(transpose(end(10:19,*)),10,num—bands)

end3=reform(transpose(end(20:29,*)),10,num—bands)

end4=reform(transpose(end(30:39,*)),10,num—bands)

img=reform(img,num—pixels,num—bands)

img1=reform(transpose(img),num—pixels,num—bands)

oMtlab=obj—new(′IDLcomIDispatchS|ProgIdS|Matlab.Application.7.8′)

oMtlab-gt;setproperty,visible=1

oMtlab-gt;putworkspacedata,′p1′,′base′,double(end1)

oMtlab-gt;putworkspacedata,′p2′,′base′,double(end2)

oMtlab-gt;putworkspacedata,′p3′,′base′,double(end3)

oMtlab-gt;putworkspacedata,′p4′,′base′,double(end4)

oMtlab-gt;putworkspacedata,′mx′,′base′,double(img1)

oMtlab-gt;Execute,′C:Program Files (x86)MATLABR2009a′

oMtlab-gt;Execute,′[abundances, rec]=AAM(mx,p1,p2,p3,p4);′

oMtlab-gt;GetWorkSpaceData,′abundances′,′base′,abundence

unmixing=transpose(reform(abundence,4,num—pixels))

envi—write—envi—file,reform(unmixing,num—cols,num—rows,4),out—dt=4,out—name=′E:AAM.img′

上述代码用end变量定义端元数组的大小,然后从硬盘中读取端元数据。AAM算法是对每一个类别的端元矩阵进行处理,所以需要将每个类别的端元矩阵单独传递。由于IDL与Matlab的存储方式相反,因此同时运用IDL的transpose(转置函数)和reform(数组行列改变函数),将IDL的端元矩阵输入到Matlab程序之中。同时,AAM解混算法是对整体影像进行解混,所以遥感影像的输入与端元矩阵一样。然后,调用IDL的面向对象的类函数obj_new(),以此指向Matlab引擎,通过Matlab引擎的PutWorkspaceData将IDL的数据输入到Matlab引擎之中,参与数学运算。通过Matlab的执行命令execute,将增加M语言编写的AAM.m程序所在的路径。由于需要将Matlab的结果输入到IDL进行成图与分析,所以输出到IDL中时transpose与reform函数与输入到Matlab相反使用。最后,调用envi_write_envi_file函数,将Matlab中的结果保存到硬盘(保存为ENVI标准格式,包含影像AAM.img与头文件AAM.hdr),从而为遥感影像后处理做好准备。

NL的调用及输出代码与AAM解混算法相似,唯一不同的是，NL是将整个光谱库端元矩阵输入到Matlab中。由于AAM与NL解混算法没有考虑地物的空间信息,因此这里对解混后的影像运用PLR算法增加空间信息。由于篇幅限制,PLR和NL代码从略。

5 结果与分析

为了验证AAM与NL模型的解混精度和PLR聚类处理的效果,使用融合后的ALI分类影像作为真值,同时利用均方根误差(RMSE)、相关系数(R)指标来进行精度评价。针对AAM模型和NL模型,按照类别对解混结果进行求和与归一化[23],结果分别见图6、图7(见封二),结果精度指标对比见表1。分析图6、图7可知:AAM模型对植被、未利用地、建筑用地和水体及阴影的解混结果都优于NL模型。结合表1分析,AAM模型对植被、未利用地、建筑用地的解混精度高于NL模型。对比图7、图8、图9、图10(见封二)可知,AAM模型与NL模型对植被、未利用地、建筑用地解混较好,但对水体及阴影解混结果较差。

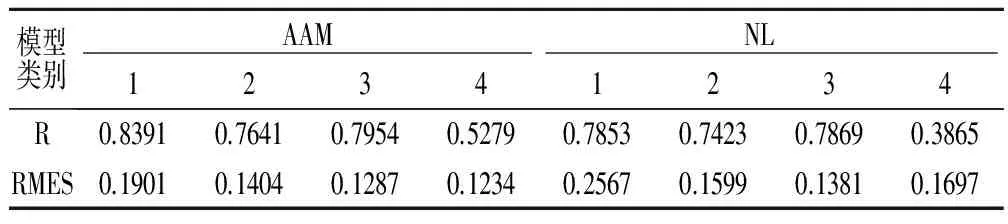
表1 AAM模型与NL模型解混影像指标对比

注:1为植被、2为未利用地、3为建筑用地、4为水体及阴影。

针对AAM与NL模型解混结果,采用PLR聚类处理,其结果见图7、图8,结果精度指标对比见表2。对比分析图7、图8和图9、图10,经过PLR处理后的AAM与NL模型解混结果对植被、未利用地、建筑用地和水体及阴影的解混结果优于没有经过PLR处理后的解混结果。同时,分析表1和表2,PLR处理后的解混结果的相关系数增加,均方根误差减少,解混精度提高。综合两种情况对比,PLR处理对解混结果有很好的校正,使植被、未利用地、建筑用地的解混结果与真值接近。PLR处理NL的解混结果,对水体和阴影有明显提高,但与真值相差太远,而PLR处理AAM的解混结果与真值接近。

表2 AAM模型与NL模型经PIL模型聚类后解混影像指标对比

综上所述,AAM模型对植被、未利用地、建筑用地、水体与阴影的解混精度高于NL模型。在PLR模型修正解混算法中忽略空间信息的不足,使解混结果明显优于未经过PLR处理的结果,对解混精度有很好的校正,降低了解混误差。PLR算法弥补了解混中空间信息的丢失,使解混结果精度提高,说明解混时考虑像元空间领域信息可提高解混精度,这对混合像元分解领域是一个新的思路。

6 结论与展望

本文针对Hyperion影像提出了一种IDL与MATLAB混合编程的影像处理方法,比较了AAM与NL端元变化解混模型的精度,采用PLR算法对两种解混的结果进行校正。试验表明，IDL与MATLAB混合编程和PLR模型在遥感影像处理中的可行性与应用前景,并得出以下结论:①IDL和MATLAB混合编程在进行Hyperion影像混合像元解混处理时结合了两者的优势,提高了程序编写效率。②在研究区中,当某种地物类别所占面积较大时,AAM与NL都有较高的解混精度；但当某种地物类别所占面积较小时,AAM与NL的解混精度低,其中AAM模型的解混精度高于NL模型。③在研究区中,经过PLR处理后的解混精度明显提高,其中地物类别所占面积越大,校正结果越明显。

PLR对影像进行混合像元解混结果校正时,补充解混算法忽略了空间信息,从而提高了解混结果的精度,但其空间邻域的运算放在后处理部分,以后考虑在解混过程中增加空间信息[24]。

[1]胡茂桂,王劲峰.遥感影像混合像元分解及超分辨率重建研究进展[J].地理科学进展,2010,29(6)∶747-756.

[2]Keshava N,Mustard J F.Spectral Unmixing[J].IEEE Signal Processing Magazine,2002,19(1)∶44-57.

[3]Bioucas Dias J M,Plaza A,Dobigeon N,etal.Hyperspectral Unmixing Overview：Geometrical,Statistical,and Sparse Regression-based Approaches[J].IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing,2012,5(2)∶354-379.

[4]Zare A,Ho K.Endmember Variability in Hyperspectral Analysis：Addressing Spectral Variability During Spectral Unmixing[J].IEEE Signal Processing Magazine,2014,31(1)∶95-104.

[5]Halimi A,Dobigeon N,Tourneret J Y.Unsupervised Unmixing of Hyperspectral Images Accounting for Endmember Variability[J].IEEE Transactions on Image Processing,2015,24(12)∶4904-4917.

[6]Roberts D A,Gardner M,Church R,etal.Mapping Chaparral in the Santa Monica Mountains Using Multiple Endmember Spectral Mixture Models[J].Remote Sensing of Environment,1998,65(3)∶267-279.

[7]Bateson C A,Asner G P,Wessman C A.Endmember Bundles：A New Approach to Incorporating Endmember Variability into Spectral Mixture Analysis[J].IEEE Transactions on Geoscience and Remote Sensing,1999,38(2)∶1083-1094.

[8]Goenaga M,Torres-Madronero M,Velez-Reyes M.etal.Unmixing Analysis of a Time Series of Hyperion Images over the Guánica Dry Forest in Puerto Rico[J].IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing,2013,6(2)∶329-338.

[9]Somers B,Zortea M,Plaza A,etal.Automated Extraction of Image----Based Endmember Bundles for Improved Spectral Unmixing[J].IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing,2012,5(2)∶396-408.

[10]Roberts D A,Gardner M,Church R,etal.Mapping Chaparral Endmember Spectral Mixture Models[J].Remote Sensing of Environment,1998,(65)∶267-279.

[11]Eches O,Dobigeon N,Mailhes C,etal.Bayesianestimation of Linear Mixtures Using the Normal Compositional Model Application to Hyperspectral Imagery[J].IEEE Transactions on Image Process,2010,19(6)∶1403-1413.

[12]Stein D.Application of the Normal Compositional Model to the Analysis of Hyperspectral Imagery[C].in Proc[Z].IEEE Workshop on Advance in Techniques for Analysis of Remote Sensing Data,2003∶44-51.

[13]于洋,周学伟,赵亚威.COM组件在实现VB调用MATLAB中的应用[J].计算机工程与科学,2008,30(5)∶110-112.

[14]麦麦提吐尔逊·艾则孜,海米提·依米提,祖皮艳木·买买提,等.焉耆盆地土地利用变化对生态服务价值的影响[J].水土保持研究,2012,19(6)∶137-141.

[15]王水献,王云智,董新光.焉耆盆地浅层地下水埋深与TDS时空变异及水化学的演化特征[J].灌溉排水学报,2007,26(5)∶90-93.

[16]石瑞花,李霞,董新光,等.焉耆盆地天然植被与地下水关系研究[J].自然资源学报,2009,24(12)∶2096-2103.

[17]Chander G, Markham B L,Helder D L.Summary of Current Radiometric Calibration Coefficients for Landsat MSS,TM,ETM+,and EO-1 ALI Sensors[J].Remote Sensing of Environment,2009,113(5)∶893-903.

[18]Heinz D C,Chang C.Fully Constrained Least Squares Linear Spectral Mixture Analysis Method for Material Quantification in Hyperspectral Imagery[J]. IEEE Transactions on Geoscience and Remote Sensing,2001,39(3)∶529-545.

[19]Heylen R,Zare A,Gader P D,etal.Hyperspectral Unmixing With Endmember Variability via Alternating Angle Minimization[J].IEEE Transactions on Geoscience and Remote Sensing,2016,54(8)∶4983-4993.

[20]Halimi A,Honeine P,Bioucasdias J M,etal.Hyperspectral Unmixing in Presence of Endmember Variability,Nonlinearity,or Mismodeling Effects[J].IEEE Transactions on Image Processing,2015,25(10)∶4565-4579.

[21]Jia X,Richards J A,Ricken D E.Remote Sensing Digital Image Analysis[M].Springer-Verlag,1999∶209-218.

[22]张俊,周成虎,李建新.新疆焉耆盆地绿洲景观的空间格局及其变化[J].地理研究,2006,25(2)∶350-359.

[23]Veganzones M A,Drumetz L,Tochon G,etal.A New Extended Linear Mixing Model to Address Spectral Variability[C].Workshop on Hyperspectral Image and Signal Processing：Evolution in Remote Sensing,2014,6(6)∶1-5.

[24]Iordache M D,Bioucas-Dias J,Plaza A.Total Variation Spatial Regularization for Sparse Hyperspectral Unmixing Sparse Regression for Hyperspectral Unmixing[J].IEEE Transactions on Geosciences and Remote Sensing.2012,50(11)∶4484-4502.

ComparisonAnalysisBetweenTwoSpectralMixtureAnalysisMethodsofIncorporatingEndmemberVariability

DUAN Jin-liang,WANG Jie,WEN Xing-yue
(College of Land and Resources,China West Normal University,Nanchong 637009,China)

Spectral mixing analysis was of great significance to improve the classification of remote sensing images.The processing of the change in endmember was the key to improving the solution.Many algorithms were proposed to solve the problem,but there were still some problems.For example,the poor operation efficiency of the algorithm,ignoring the high orer interaction of the endmembers,and missing some information in the spatial domain.To solve problems above,based on the combination of IDL and MATLAB mixed programming,this paper used the alternate deterministic model minimum angle method and statistical model for the sake of the nonlinear algorithm of high order terms of endmember unmixing changes within the Hyperion images,and the probabilistic relaxation labeling on pixel space field information was used to improve the unmixing accuracy.The experimental results showed that both the deterministic model and the statistical model could obtain a high degree of unmixing accuracy when a certain object category occupied a large area in a image.When the area occupied by the object category was small,the deterministic model′s accuracy was superior to the statistical model.In addition,when the field information of the pixel space was supplemented,the result of the unmixing could be corrected.

hyperion image;spectral endmember variability unmixing;IDL and MATLAB;alternating angle minimization;nonlinear mixing model

10.3969/j.issn.1005-8141.2017.06.002

TP751.1

A

1005-8141(2017)06-0651-05

2017-04-17；

2017-05-15

国家自然科学基金面上项目(编号:41671220);西华师范大学博士科研启动基金项目(编号:412546、412547);四川省教育厅自然科学基金重点项目(编号:15ZA150)。

段金亮(1994-),男,四川省达州人,本科,主要从事遥感数字图像处理工作。

王杰(1984-),男,四川省南充人,博士,讲师,主要从事遥感数字图像处理、数据挖掘研究工作。